Arithmetic Where weve been Performance seconds cycles instructions

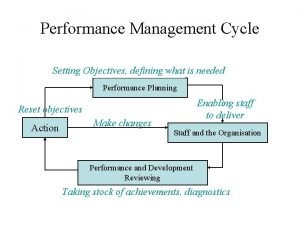
Arithmetic • Where we've been: – Performance (seconds, cycles, instructions) – Abstractions: Instruction Set Architecture Assembly Language and Machine Language • What's up ahead: – Implementing the Architecture 1998 Morgan Kaufmann Publishers
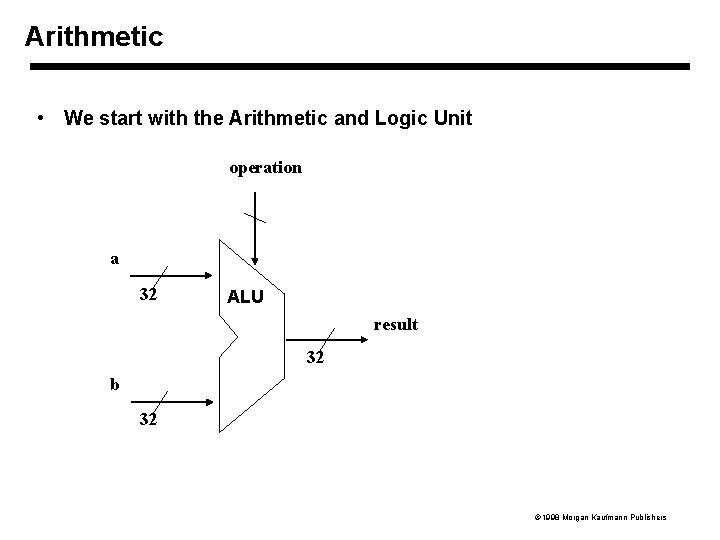
Arithmetic • We start with the Arithmetic and Logic Unit operation a 32 ALU result 32 b 32 1998 Morgan Kaufmann Publishers

Numbers • Bits are just bits (no inherent meaning) — conventions define relationship between bits and numbers • Binary numbers (base 2) 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001. . . decimal: 0. . . 2 n-1 • Of course it gets more complicated: numbers are finite (overflow) fractions and real numbers negative numbers • How do we represent negative numbers? i. e. , which bit patterns will represent which numbers? • Octal and hexadecimal numbers • Floating-point numbers 1998 Morgan Kaufmann Publishers

Possible Representations of Signed Numbers • Sign Magnitude: 000 = +0 001 = +1 010 = +2 011 = +3 100 = -0 101 = -1 110 = -2 111 = -3 One's Complement 000 = +0 001 = +1 010 = +2 011 = +3 100 = -3 101 = -2 110 = -1 111 = -0 Two's Complement 000 = +0 001 = +1 010 = +2 011 = +3 100 = -4 101 = -3 110 = -2 111 = -1 • Issues: balance, number of zeros, ease of operations. • Two’s complement is best. 1998 Morgan Kaufmann Publishers

MIPS • 32 bit signed numbers: 0000 00002 = 010 0000 0000 00012 = +110 0000 0000 00102 = +210. . . 0111 1111 1111 11102 = +2, 147, 483, 64610 0111 1111 11112 = +2, 147, 483, 64710 1000 0000 00002 = – 2, 147, 483, 64810 1000 0000 0000 00012 = – 2, 147, 483, 64710 1000 0000 0000 00102 = – 2, 147, 483, 64610. . . 1111 1111 11012 = – 310 1111 1111 11102 = – 210 1111 11112 = – 110 maxint minint 1998 Morgan Kaufmann Publishers

Two's Complement Operations • Negating a two's complement number: invert all bits and add 1 – Remember: “Negate” and “invert” are different operations. You negate a number but invert a bit. • Converting n bit numbers into numbers with more than n bits: – MIPS 16 bit immediate gets converted to 32 bits for arithmetic – copy the most significant bit (the sign bit) into the other bits 0010 -> 0000 0010 1010 -> 1111 1010 "sign extension" – MIPS load byte instructions lbu: no sign extension lb: sign extension 1998 Morgan Kaufmann Publishers

Addition & Subtraction • Unsigned numbers just like in grade school (carry/borrow 1 s) 0111 0110 + 0110 - 0101 1101 0001 • Two's complement operations easy – subtraction using addition of opposite number 0111 + 1010 10001 • (result is 0001, carry bit is set) Two's complement overflow (result not within number range) – e. g. , adding two 4 -bit numbers does not yield an 4 -bit number 0111 + 0011 1010 (result is - 6, overflow bit is set) 1998 Morgan Kaufmann Publishers

Detecting Overflow • No overflow when adding a positive and a negative number • No overflow when signs are the same for subtraction • Overflow occurs when the value affects the sign: – overflow when adding two positives yields a negative – or, adding two negatives gives a positive – or, subtract a negative from a positive and get a negative – or, subtract a positive from a negative and get a positive • Consider the operations A + B, and A – B – Can overflow occur if B is 0 ? No. – Can overflow occur if A is 0 ? Yes. 1998 Morgan Kaufmann Publishers

Effects of Overflow • An exception (interrupt) occurs – Control jumps to predefined address for exception – Interrupted address is saved for possible resumption • Details based on software system / language – example: flight control vs. homework assignment • Don't always want to detect overflow — new MIPS instructions: addu, addiu, subu note: addiu still sign-extends! note: sltu, sltiu for unsigned comparisons 1998 Morgan Kaufmann Publishers

Logical Operations • • and, andi: or, ori: sll: slr: bit-by-bit AND bit-by-bit OR shift left logical shift right logical • 0101 1010 shifting left two steps gives 0110 1000 • 0110 1010 shifting right three bits gives 0000 1011 1998 Morgan Kaufmann Publishers
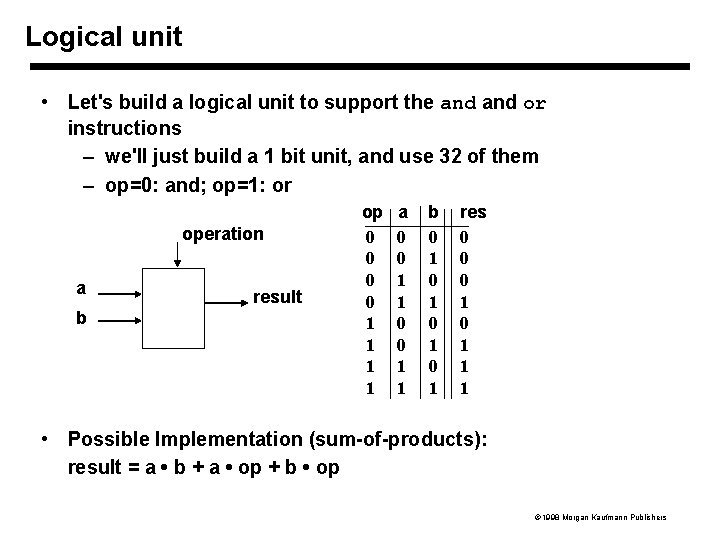
Logical unit • Let's build a logical unit to support the and or instructions – we'll just build a 1 bit unit, and use 32 of them – op=0: and; op=1: or operation a b result op 0 0 1 1 a 0 0 1 1 b 0 1 0 1 res 0 0 0 1 1 1 • Possible Implementation (sum-of-products): result = a • b + a • op + b • op 1998 Morgan Kaufmann Publishers
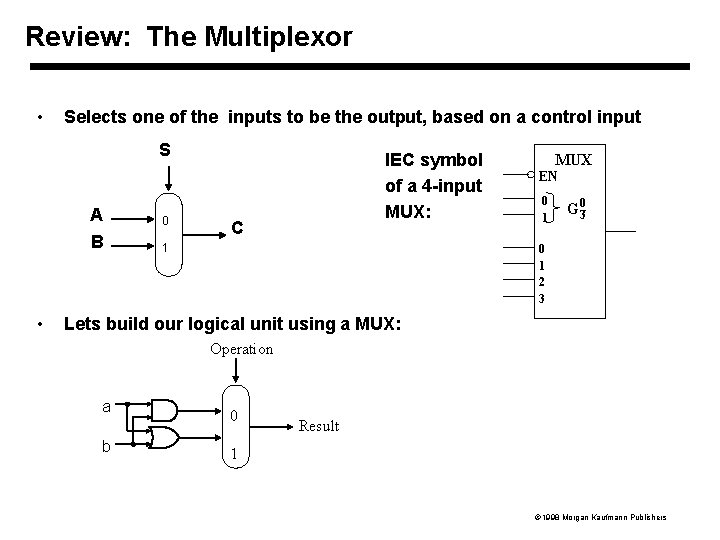
Review: The Multiplexor • Selects one of the inputs to be the output, based on a control input S • A 0 B 1 IEC symbol of a 4 -input MUX: C MUX EN 0 1 G _03 0 1 2 3 Lets build our logical unit using a MUX: Operation a b 0 Result 1 1998 Morgan Kaufmann Publishers
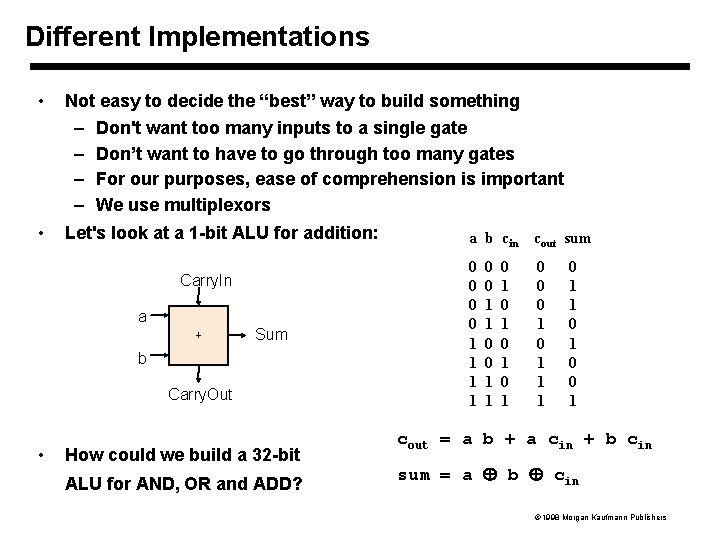
Different Implementations • Not easy to decide the “best” way to build something – Don't want too many inputs to a single gate – Don’t want to have to go through too many gates – For our purposes, ease of comprehension is important – We use multiplexors • Let's look at a 1 -bit ALU for addition: a b cin cout sum 0 0 1 1 Carry. In a Sum b Carry. Out • How could we build a 32 -bit ALU for AND, OR and ADD? 0 0 1 1 0 1 0 1 0 0 0 1 1 1 0 1 0 0 1 cout = a b + a cin + b cin sum = a b cin 1998 Morgan Kaufmann Publishers
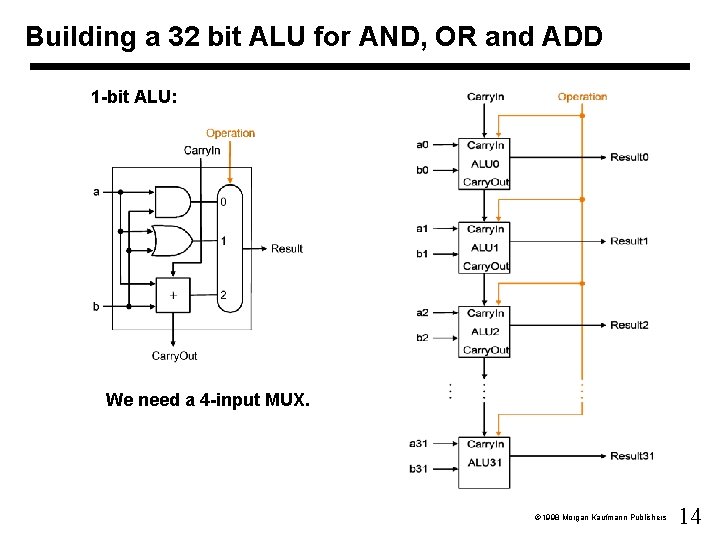
Building a 32 bit ALU for AND, OR and ADD 1 -bit ALU: We need a 4 -input MUX. 1998 Morgan Kaufmann Publishers 14
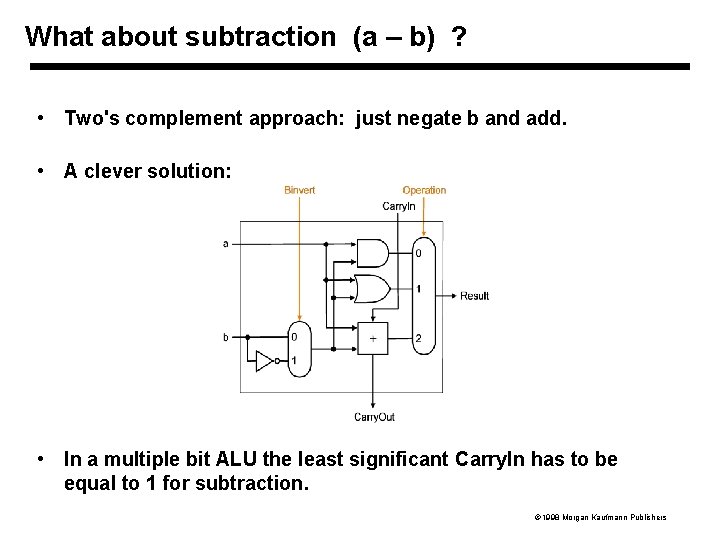
What about subtraction (a – b) ? • Two's complement approach: just negate b and add. • A clever solution: • In a multiple bit ALU the least significant Carry. In has to be equal to 1 for subtraction. 1998 Morgan Kaufmann Publishers

Tailoring the ALU to the MIPS • Need to support the set-on-less-than instruction (slt) – remember: slt is an arithmetic instruction – produces a 1 if rs < rt and 0 otherwise – use subtraction: (a-b) < 0 implies a < b • Need to support test for equality (beq $t 5, $t 6, $t 7) – use subtraction: (a-b) = 0 implies a = b 1998 Morgan Kaufmann Publishers
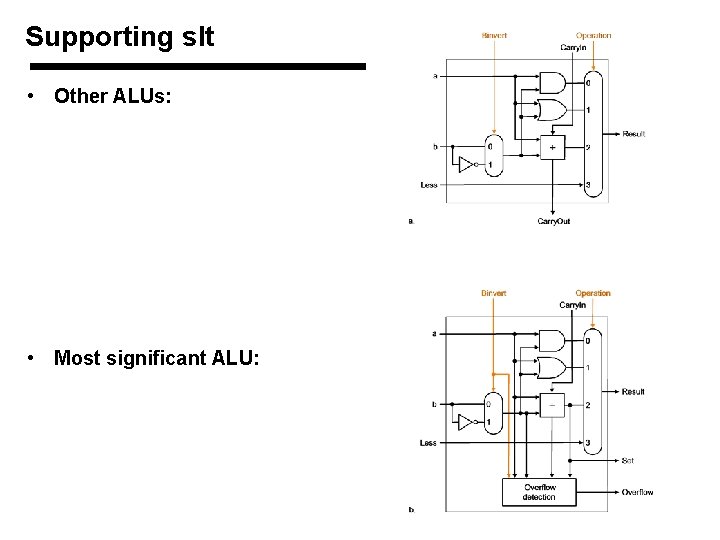
Supporting slt • Other ALUs: • Most significant ALU:
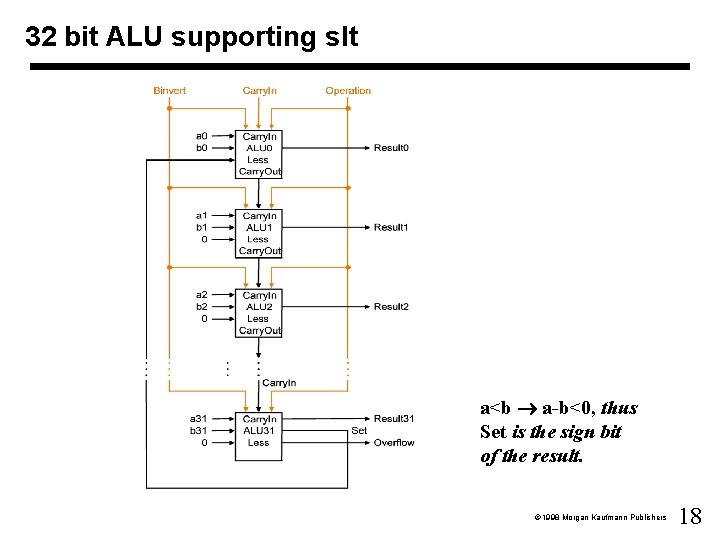
32 bit ALU supporting slt a<b a-b<0, thus Set is the sign bit of the result. 1998 Morgan Kaufmann Publishers 18
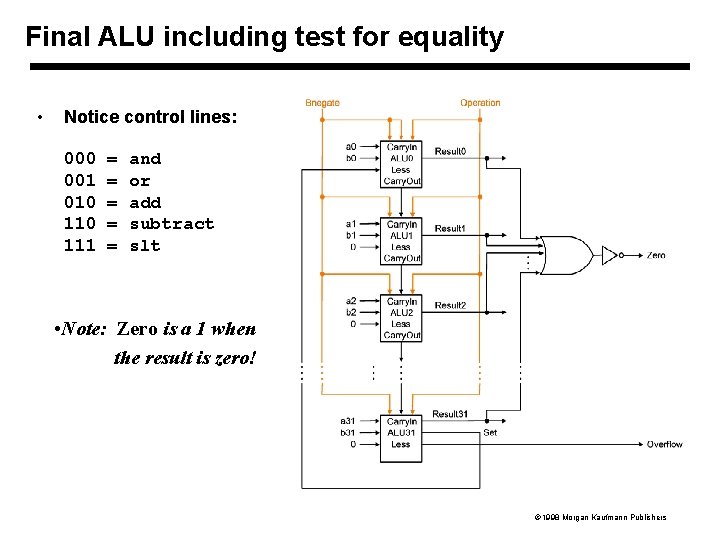
Final ALU including test for equality • Notice control lines: 000 = and 001 = or 010 = add 110 = subtract 111 = slt • Note: Zero is a 1 when the result is zero! 1998 Morgan Kaufmann Publishers

Conclusion • We can build an ALU to support the MIPS instruction set – key idea: use a multiplexor to select the output we want – we can efficiently perform subtraction using two’s complement – we can replicate a 1 -bit ALU to produce a 32 -bit ALU • Important points about hardware – all of the gates are always working – the speed of a gate is affected by the number of inputs to the gate – the speed of a circuit is affected by the number of gates in series (on the “critical path” or the “deepest level of logic”) 1998 Morgan Kaufmann Publishers

Conclusion • Our primary focus: comprehension, however, – clever changes to organization can improve performance (similar to using better algorithms in software) – we’ll look at examples for addition, multiplication and division 1998 Morgan Kaufmann Publishers

Problem: ripple carry adder is slow • A 32 -bit ALU is much slower than a 1 -bit ALU. • There are more than one way to do addition. – the two extremes: ripple carry and sum-of-products Can you see the ripple? c 1 = b 0 c 0 + a 0 b 0 c 2 = b 1 c 1 + a 1 b 1 c 3 = b 2 c 2 + a 2 b 2 c 4 = b 3 c 3 + a 3 b 3 How could you get rid of it? c 2 = c 2(a 0, b 0, c 0, a 1, b 1) c 3 = c 3(a 0, b 0, c 0, a 1, b 1, a 2, b 2) c 4 = c 4(a 0, b 0, c 0, a 1, b 1, a 2, b 2, a 3, b 3) Not feasible! Too many inputs to the gates. 1998 Morgan Kaufmann Publishers

Carry-lookahead adder • An approach in-between the two extremes • Motivation: – If we didn't know the value of carry-in, what could we do? – When would we always generate a carry? gi = ai bi – When would we propagate the carry? pi = ai + bi – Look at the truth table! • Did we get rid of the ripple? c 1 = g 0 + p 0 c 0 c 2 = g 1 + p 1 c 1 c 2 = g 1+p 1 g 0+p 1 p 0 c 0 c 3 = g 2 + p 2 c 2 c 3 = g 2+p 2 g 1+p 2 p 1 g 0+p 2 p 1 p 0 c 0 c 4 = g 3 + p 3 c 3 c 4 =. . . Feasible! A smaller number of inputs to the gates. 1998 Morgan Kaufmann Publishers
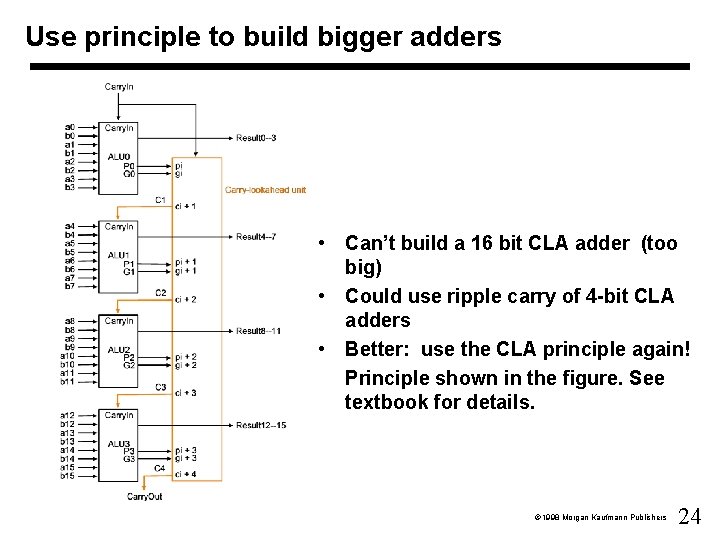
Use principle to build bigger adders • Can’t build a 16 bit CLA adder (too big) • Could use ripple carry of 4 -bit CLA adders • Better: use the CLA principle again! Principle shown in the figure. See textbook for details. 1998 Morgan Kaufmann Publishers 24

Multiplication • More complicated than addition – can be accomplished via shifting and addition • More time and more area • Let's look at 2 versions based on grammar school algorithm 0010 (multiplicand) x_1011 (multiplier) 0010 0000 0010___ 0010110 • Negative numbers: – easy way: convert to positive and multiply – there are better techniques 1998 Morgan Kaufmann Publishers
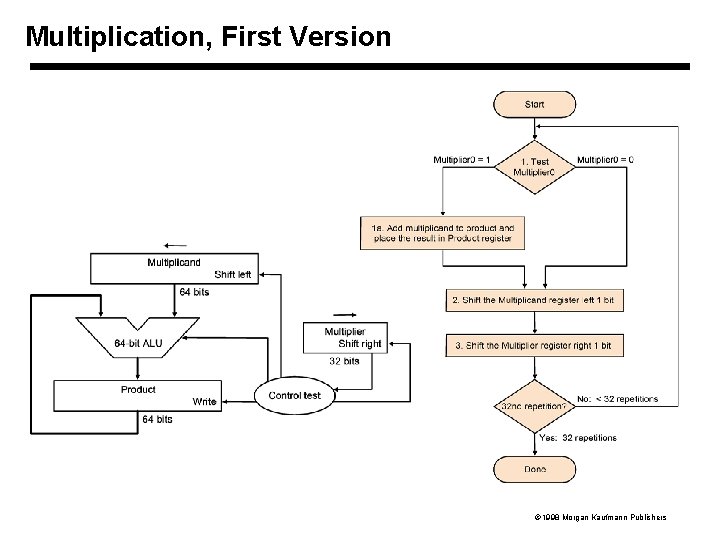
Multiplication, First Version 1998 Morgan Kaufmann Publishers
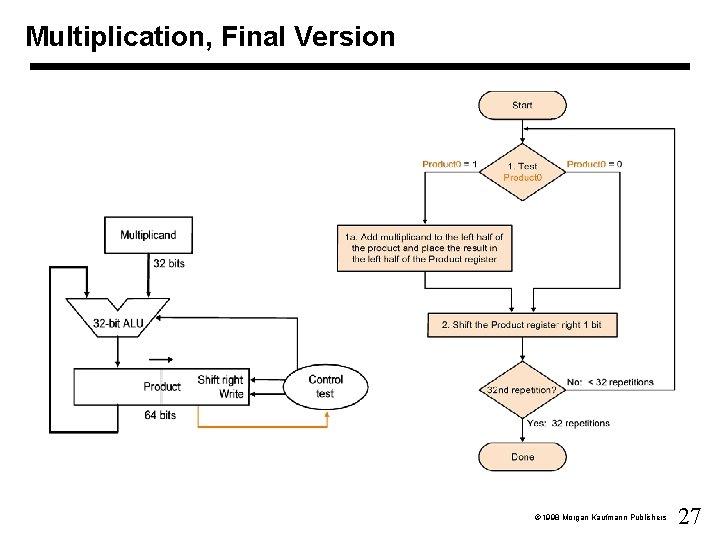
Multiplication, Final Version 1998 Morgan Kaufmann Publishers 27

Booth’s Algorithm • The grammar school method was implemented using addition and shifting • Booth’s algorithm also uses subtraction • Based on two bits of the multiplier either add, subtract or do nothing; always shift • Handles two’s complement numbers 1998 Morgan Kaufmann Publishers

Fast multipliers • Combinational implementations – Conventional multiplier algorithm • partial products with AND gates • adders – Lots of modifications • Sequential implementations – Pipelined multiplier • registers between levels of logic • result delayed • effective speed of multiple multiplications increased 1998 Morgan Kaufmann Publishers

Four-Bit Binary Multiplication Multiplicand Multiplier 1 st partial product 2 nd partial product A 1 B 0 3 rd partial product 4 th partial product Final product + P 7 A 3 B 3 P 6 A 2 B 3 A 3 B 2 P 5 A 2 B 2 A 3 B 1 P 4 B 3 B 2 B 1 B 0 A 3 A 2 A 1 A 0 B 3 A 0 B 2 A 0 B 1 A 0 B 0 A 1 B 3 A 1 B 2 A 1 B 1 A 2 B 1 A 3 B 0 P 3 A 2 B 0 P 2 P 1 P 0 1998 Morgan Kaufmann Publishers
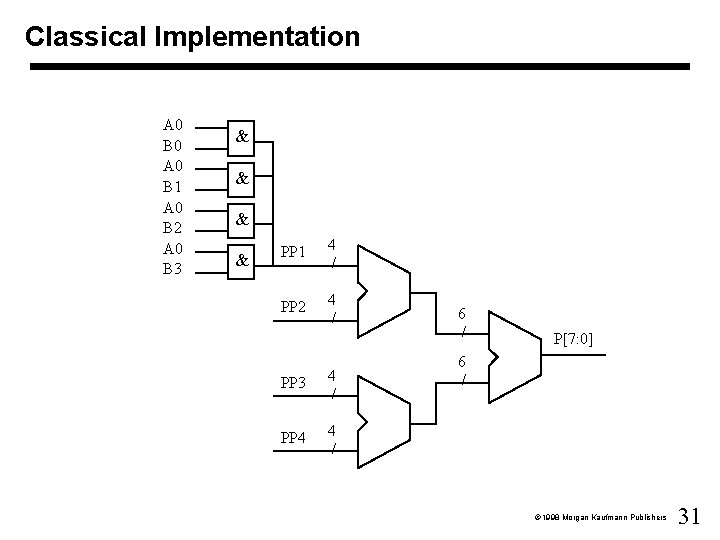
Classical Implementation A 0 B 0 A 0 B 1 A 0 B 2 A 0 B 3 & & PP 1 4 / PP 2 4 / PP 3 4 / PP 4 4 / 6 / P 7: 0 6 / 1998 Morgan Kaufmann Publishers 31
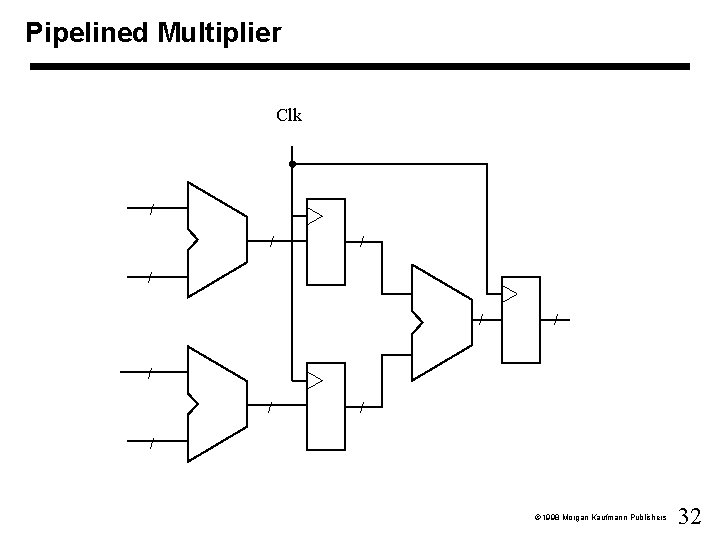
Pipelined Multiplier Clk / / / / / 1998 Morgan Kaufmann Publishers 32

Division • Simple method: – Initialise the remainder with the dividend – Start from most significant end – Subtract divisor from the remainder if possible (quotient bit 1) – Shift divisor to the right and repeat 1998 Morgan Kaufmann Publishers
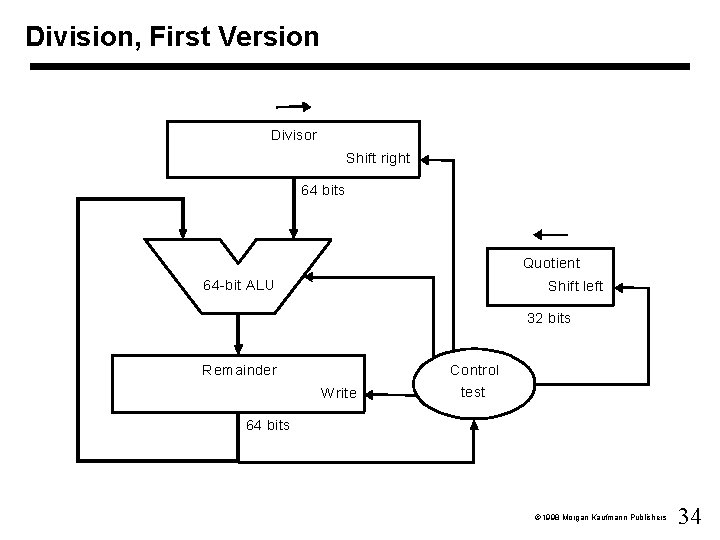
Division, First Version Divisor Shift right 64 bits Quotient 64 -bit ALU Shift left 32 bits Control R emainder Write test 64 bits 1998 Morgan Kaufmann Publishers 34
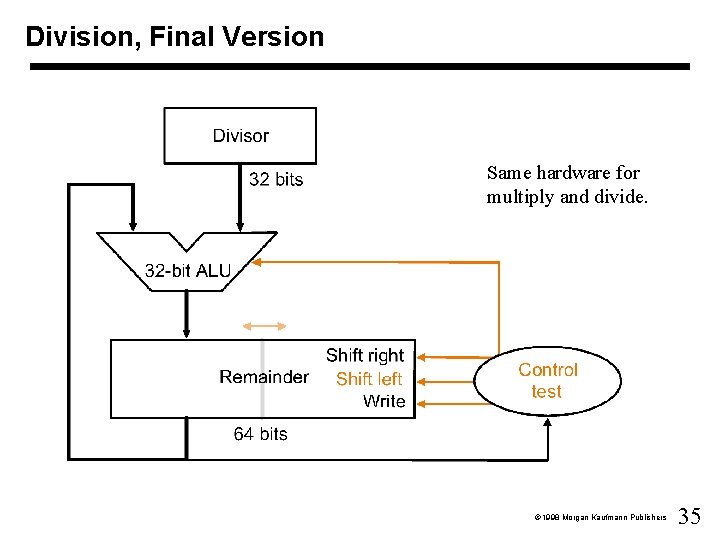
Division, Final Version Same hardware for multiply and divide. 1998 Morgan Kaufmann Publishers 35

Floating Point (a brief look) • We need a way to represent – numbers with fractions, e. g. , 3. 1416 – very small numbers, e. g. , . 00001 – very large numbers, e. g. , 3. 15576 109 • Representation: – sign, exponent, significand: (– 1)sign significand 2 exponent – more bits for significand gives more accuracy – more bits for exponent increases range • IEEE 754 floating point standard: – single precision: 8 bit exponent, 23 bit significand – double precision: 11 bit exponent, 52 bit significand 1998 Morgan Kaufmann Publishers

IEEE 754 floating-point standard • Leading “ 1” bit of significand is implicit • Exponent is “biased” to make sorting easier – all 0 s is smallest exponent all 1 s is largest – bias of 127 for single precision and 1023 for double precision – summary: (– 1)significand) 2 exponent – bias • Example: – – decimal: -. 75 = -3/4 = -3/22 binary: -. 11 = -1. 1 x 2 -1 floating point: exponent = 126 = 01111110 IEEE single precision: 101111110100000000000 1998 Morgan Kaufmann Publishers

Floating-point addition 1. Shift the significand of the number with the lesser exponent right until the exponents match 2. Add the significands 3. Normalise the sum, checking for overflow or underflow 4. Round the sum 1998 Morgan Kaufmann Publishers
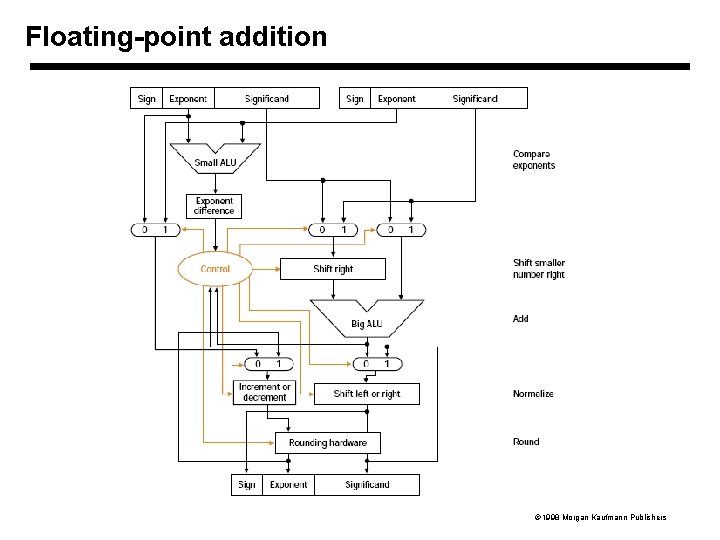
Floating-point addition 1998 Morgan Kaufmann Publishers

Floating-point multiplication 1. 2. 3. 4. 5. Add the exponents Multiply the significands Normalise the product, checking for overflow or underflow Round the product Find out the sign of the product 1998 Morgan Kaufmann Publishers

Floating Point Complexities • Operations are somewhat more complicated (see text) • In addition to overflow we can have “underflow” • Accuracy can be a big problem – IEEE 754 keeps two extra bits during intermediate calculations, guard and round – four rounding modes – positive divided by zero yields “infinity” – zero divide by zero yields “not a number” – other complexities • Implementing the standard can be tricky 1998 Morgan Kaufmann Publishers

Chapter Four Summary • Computer arithmetic is constrained by limited precision • Bit patterns have no inherent meaning but standards do exist – two’s complement – IEEE 754 floating point • Computer instructions determine “meaning” of the bit patterns • Performance and accuracy are important so there are many complexities in real machines (i. e. , algorithms and implementation). • We are ready to move on (and implement the processor) 1998 Morgan Kaufmann Publishers
- Slides: 42