Arithmetic Circuits 2 EE 200 Digital Logic Circuit

Arithmetic Circuits 2 EE 200 Digital Logic Circuit Design Dr. Muhamed Mudawar King Fahd University of Petroleum and Minerals

Presentation Outline v BCD Adder v Magnitude Comparator v Binary Multiplier v Carry-Save Adders in Multipliers Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 2

BCD Addition v We use binary arithmetic to add the BCD digits 1000 + 0101 1101 8 + 5 13 (>9) v If the result is more than 9, it must be corrected to use 2 digits v To correct the digit, add 6 to the digit sum 1000 + 0101 1101 + 0110 1 0011 Arithmetic Circuits 2 Final answer in BCD 8 + 5 13 (>9) + 6 (add 6) 19 (carry + 3) EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 3

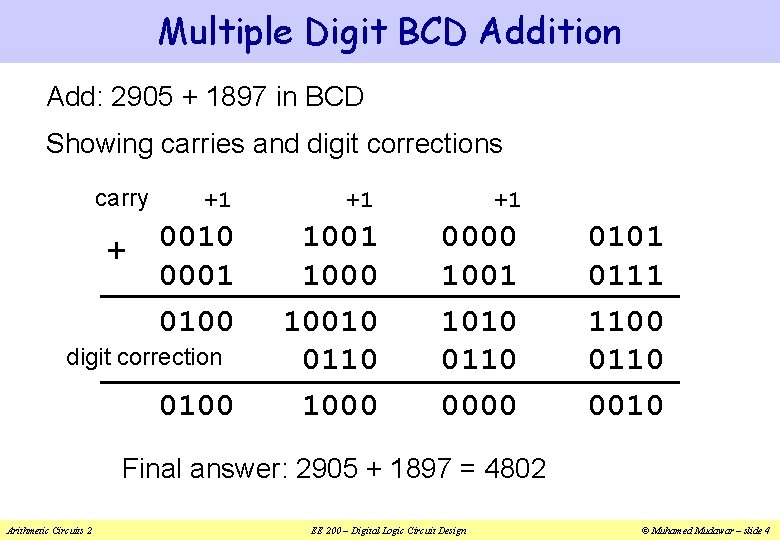
Multiple Digit BCD Addition Add: 2905 + 1897 in BCD Showing carries and digit corrections carry + +1 +1 +1 0010 0001 0100 1001 1000 10010 0110 1000 0000 1001 1010 0110 0000 digit correction 0100 0101 0111 1100 0110 0010 Final answer: 2905 + 1897 = 4802 Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 4

BCD Adder A [3: 0] B [3: 0] 4 Cout Correction is required if: A+B > 9 4 BCD Adder Cin Correction circuit adds 0 or 6 A [3: 0] 4 Detection Circuit S [3: 0] 00 01 11 10 00 B [3: 0] 4 4 4 -bit binary Adder z 3 z 2 z 1 z 0 Cin Cout 01 11 1 10 1 1 1 Correction Circuit Add 0 or 6 FA S 3 Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design S 2 HA HA = Half Adder FA = Full Adder S 1 S 0 © Muhamed Mudawar – slide 5

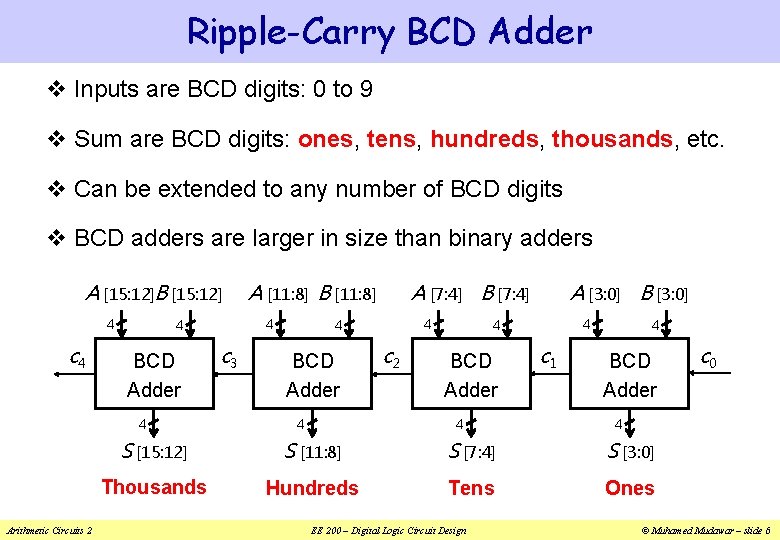
Ripple-Carry BCD Adder v Inputs are BCD digits: 0 to 9 v Sum are BCD digits: ones, tens, hundreds, thousands, etc. v Can be extended to any number of BCD digits v BCD adders are larger in size than binary adders A [15: 12]B [15: 12] 4 c 4 4 Arithmetic Circuits 2 4 4 BCD Adder A [11: 8] B [11: 8] c 3 A [7: 4] B [7: 4] 4 4 BCD Adder 4 c 2 A [3: 0] B [3: 0] 4 4 BCD Adder 4 c 1 4 BCD Adder 4 S [15: 12] S [11: 8] S [7: 4] S [3: 0] Thousands Hundreds Tens Ones EE 200 – Digital Logic Circuit Design c 0 © Muhamed Mudawar – slide 6

Next. . . v BCD Adder v Magnitude Comparator v Binary Multiplier v Carry-Save Adders in Multipliers Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 7

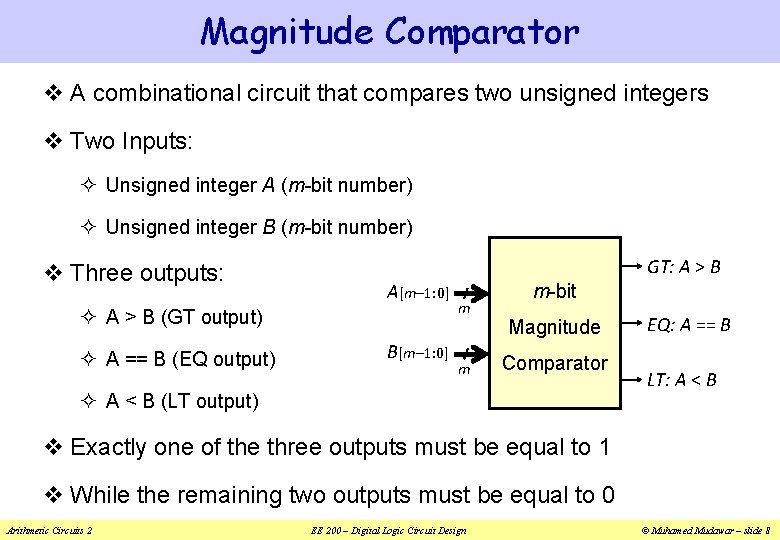
Magnitude Comparator v A combinational circuit that compares two unsigned integers v Two Inputs: ² Unsigned integer A (m-bit number) ² Unsigned integer B (m-bit number) v Three outputs: GT: A > B A[m– 1: 0] ² A > B (GT output) ² A == B (EQ output) B[m– 1: 0] m m m-bit Magnitude Comparator ² A < B (LT output) EQ: A == B LT: A < B v Exactly one of the three outputs must be equal to 1 v While the remaining two outputs must be equal to 0 Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 8

Example: 4 -bit Magnitude Comparator v Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 9

The Greater Than Output v Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 10

The Less Than Output v Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 11

Iterative Magnitude Comparator Design v Cell 3 Arithmetic Circuits 2 Cell 1 EE 200 – Digital Logic Circuit Design Cell 0 © Muhamed Mudawar – slide 12

Cell Implementation v Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 13

Next. . . v BCD Adder v Magnitude Comparator v Binary Multiplier v Carry-Save Adders in Multipliers Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 14

Binary Multiplication v Binary Multiplication is simple: 0× 0=0, 0× 1=0, Multiplicand Multiplier 1× 0=0, × 11002 = 12 11012 = 13 1100 0000 1100 Product 1× 1=1 Binary multiplication 0 × multiplicand = 0 1 × multiplicand = multiplicand 100111002 = 156 v n-bit multiplicand × n-bit multiplier = 2 n-bit product v Accomplished via shifting and addition Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 15

4 -bit × 4 -bit Binary Multiplier v Suppose we want to multiply two numbers A and B ² Example on 4 -bit numbers: A = a 3 a 2 a 1 a 0 and B = b 3 b 2 b 1 b 0 v Step 1: AND (multiply) each bit of A with each bit of B ² Requires n 2 AND gates and produces n 2 product bits ² Position of aibj = (i+j). For example, Position of a 2 b 3 = 2+3 = 5 A×B a 3 b 3 Arithmetic Circuits 2 a 3 b 0 a 2 b 0 a 1 b 0 a 3 b 1 a 2 b 1 a 1 b 1 a 0 b 1 a 3 b 2 a 2 b 2 a 1 b 2 a 0 b 2 a 2 b 3 a 1 b 3 a 0 b 3 EE 200 – Digital Logic Circuit Design a 0 b 0 © Muhamed Mudawar – slide 16

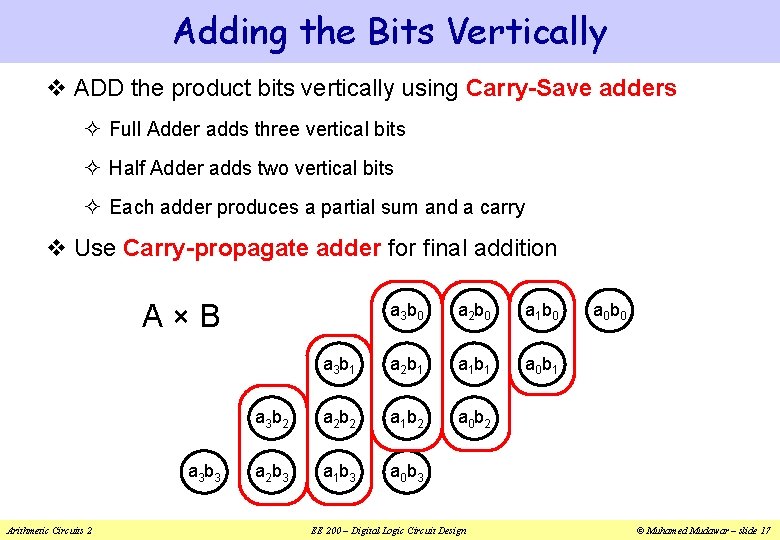
Adding the Bits Vertically v ADD the product bits vertically using Carry-Save adders ² Full Adder adds three vertical bits ² Half Adder adds two vertical bits ² Each adder produces a partial sum and a carry v Use Carry-propagate adder for final addition A×B a 3 b 3 Arithmetic Circuits 2 a 3 b 0 a 2 b 0 a 1 b 0 a 3 b 1 a 2 b 1 a 1 b 1 a 0 b 1 a 3 b 2 a 2 b 2 a 1 b 2 a 0 b 2 a 2 b 3 a 1 b 3 a 0 b 3 EE 200 – Digital Logic Circuit Design a 0 b 0 © Muhamed Mudawar – slide 17

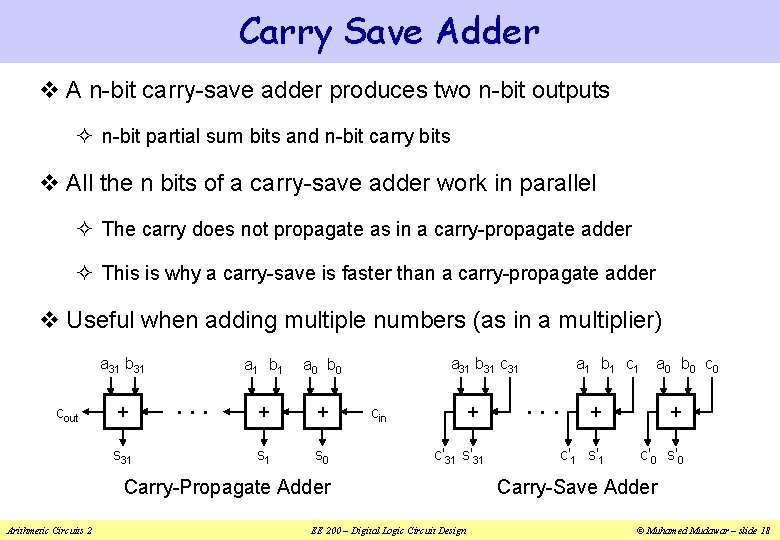
Carry Save Adder v A n-bit carry-save adder produces two n-bit outputs ² n-bit partial sum bits and n-bit carry bits v All the n bits of a carry-save adder work in parallel ² The carry does not propagate as in a carry-propagate adder ² This is why a carry-save is faster than a carry-propagate adder v Useful when adding multiple numbers (as in a multiplier) a 31 b 31 cout + s 31 . . . a 1 b 1 a 0 b 0 + + s 1 s 0 a 31 b 31 c 31 + cin c'31 s'31 Carry-Propagate Adder Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design a 1 b 1 c 1 . . . a 0 b 0 c 0 + + c'1 s'1 c'0 s'0 Carry-Save Adder © Muhamed Mudawar – slide 18

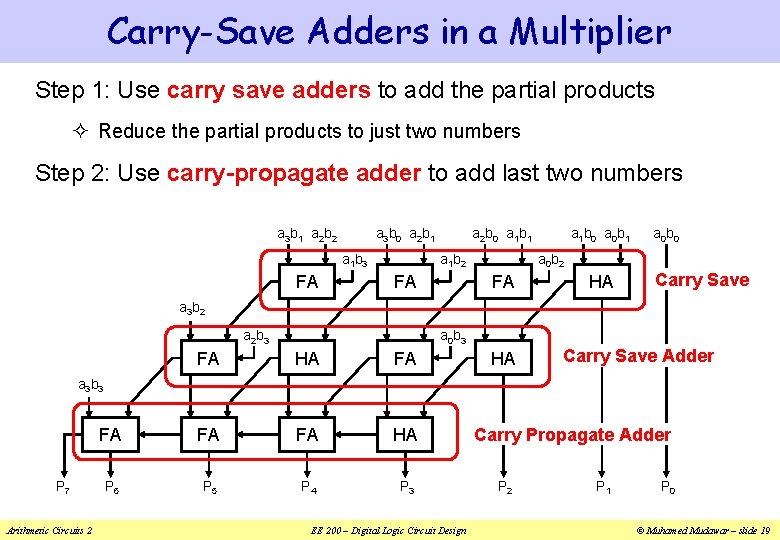
Carry-Save Adders in a Multiplier Step 1: Use carry save adders to add the partial products ² Reduce the partial products to just two numbers Step 2: Use carry-propagate adder to add last two numbers a 3 b 1 a 2 b 2 a 3 b 0 a 2 b 1 a 1 b 3 FA a 2 b 0 a 1 b 1 a 1 b 2 FA a 1 b 0 a 0 b 1 a 0 b 0 a 0 b 2 FA HA Carry Save a 3 b 2 a 2 b 3 a 0 b 3 FA HA FA FA HA P 6 P 5 P 4 P 3 HA Carry Save Adder a 3 b 3 P 7 Arithmetic Circuits 2 EE 200 – Digital Logic Circuit Design Carry Propagate Adder P 2 P 1 P 0 © Muhamed Mudawar – slide 19