Aristotles Solar System Model 350 B C Ptolemys

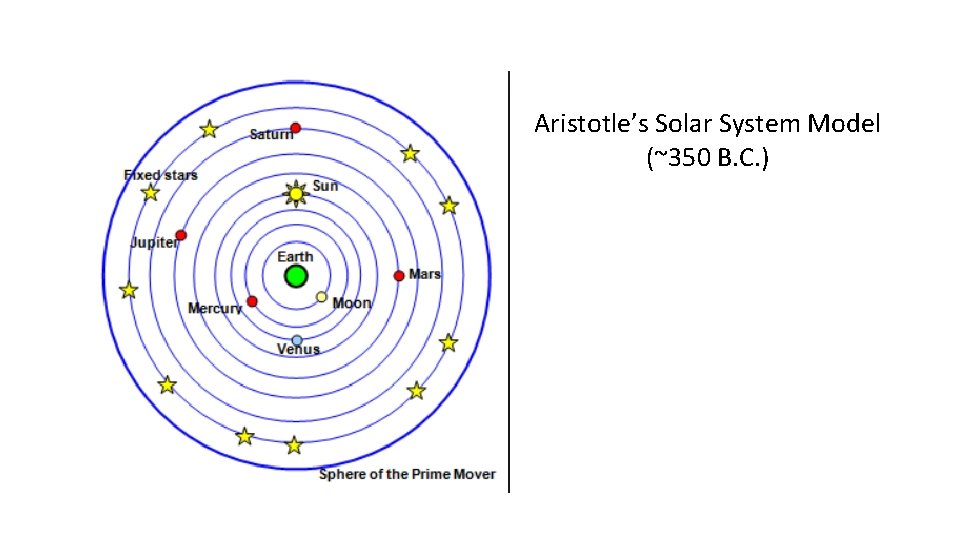
Aristotle’s Solar System Model (~350 B. C. )

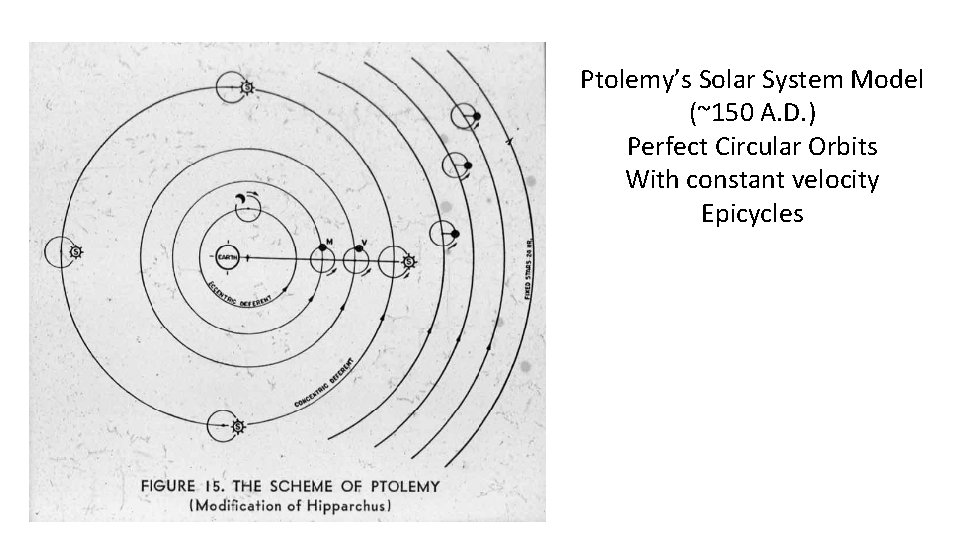
Ptolemy’s Solar System Model (~150 A. D. ) Perfect Circular Orbits With constant velocity Epicycles

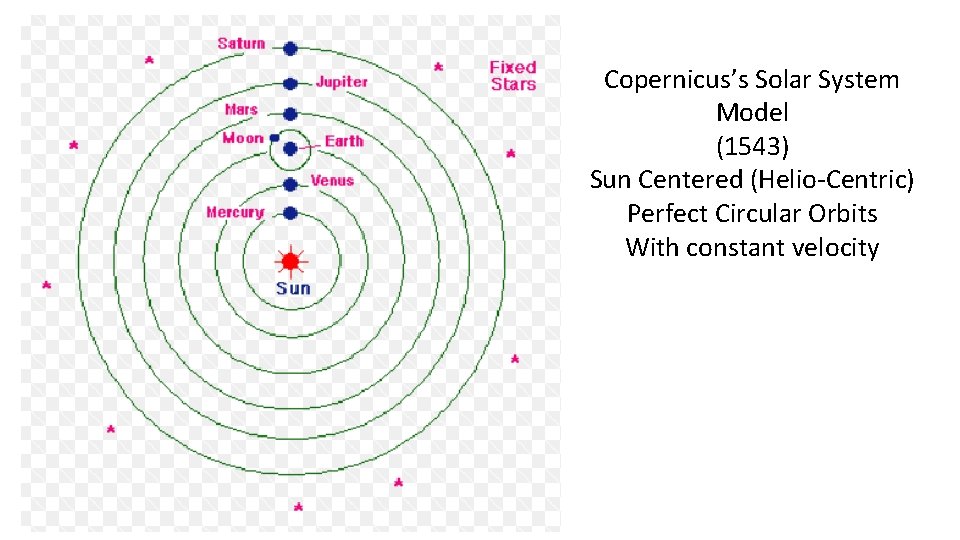
Copernicus’s Solar System Model (1543) Sun Centered (Helio-Centric) Perfect Circular Orbits With constant velocity

Thycho Brahe (born 1546) Carefully recorded planetary positions for 30 years. Generated the BEST set of planetary position data ever.

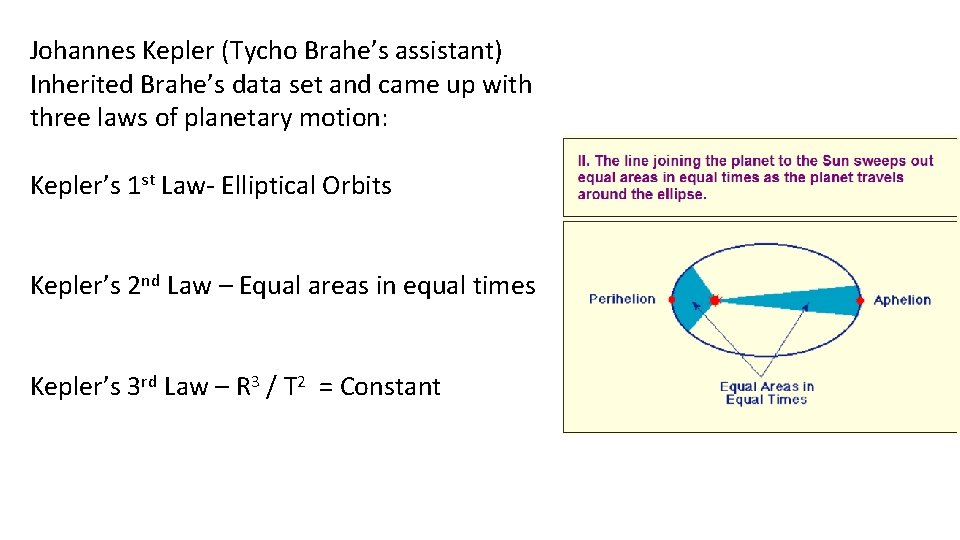
Johannes Kepler (Tycho Brahe’s assistant) Inherited Brahe’s data set and came up with three laws of planetary motion: Kepler’s 1 st Law- Elliptical Orbits Kepler’s 2 nd Law – Equal areas in equal times Kepler’s 3 rd Law – R 3 / T 2 = Constant

Galileo Galilei (~1609) First person to use a telescope to view the planets. He saw: -The moon had mountains and craters and blemishes. -The sun had black spots on it. -Venus went through phases like the moon and appeared larger and smaller. -Jupiter had “moons” that orbited it. -Saturn had “ears”.

Saturn’s Ears & Moon’s craters/mountains Jupiter and its moons

Isaac Newton (~1687) Published Principia, which included his Theory of Universal Gravitation -What if the same force that pulls me toward the ground, also pulls the moon toward the earth? w = mg Weight IS the force of gravity and it is clearly linearly proportional to my mass. (Newton’s third law of motion suggests that the force of gravity should also be proportional to the earth’s mass. ) So, Fg a m 1 m 2 And considering the acceleration of gravity at the surface of earth (9. 8 m/s 2 and the centripetal acceleration of the moon) Newton deduced that Fg a 1/R 2 Fg a m 1 m 2 /R 2 Fg = G m 1 m 2 /R 2

Fg = G m 1 m 2 /R 2 Newton’s Law of Universal Gravitation Henry Cavendish Measured G in 1797 using a torsion balance. He found that G = 6. 67 x 10 -11 Nm 2/kg 2 This was called “weighing the earth”. I’ll explain why… Now, we can use Newton’s Law of Universal Gravitation to: Find g on the surface of different planets. Find the orbital speed of satellites. Find the mass of an object that is being orbited.

Let’s find: The mass of the earth. The mass of the sun. The mass of Jupiter. The acceleration of gravity on mars. The orbital radius of a geosynchronous satellite.

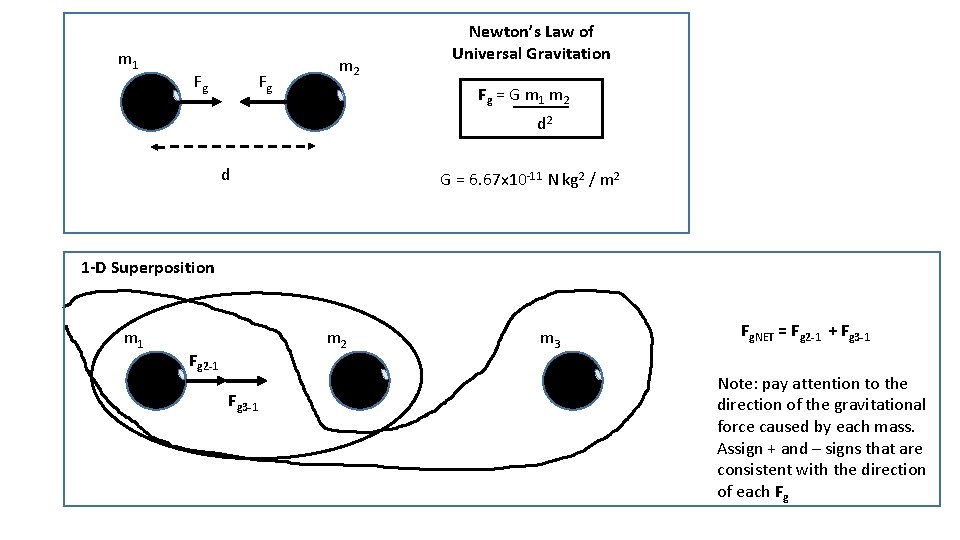
m 1 Fg Fg m 2 Newton’s Law of Universal Gravitation Fg = G m 1 m 2 d G = 6. 67 x 10 -11 N kg 2 / m 2 1 -D Superposition m 1 m 2 Fg 2 -1 Fg 3 -1 m 3 Fg. NET = Fg 2 -1 + Fg 3 -1 Note: pay attention to the direction of the gravitational force caused by each mass. Assign + and – signs that are consistent with the direction of each Fg

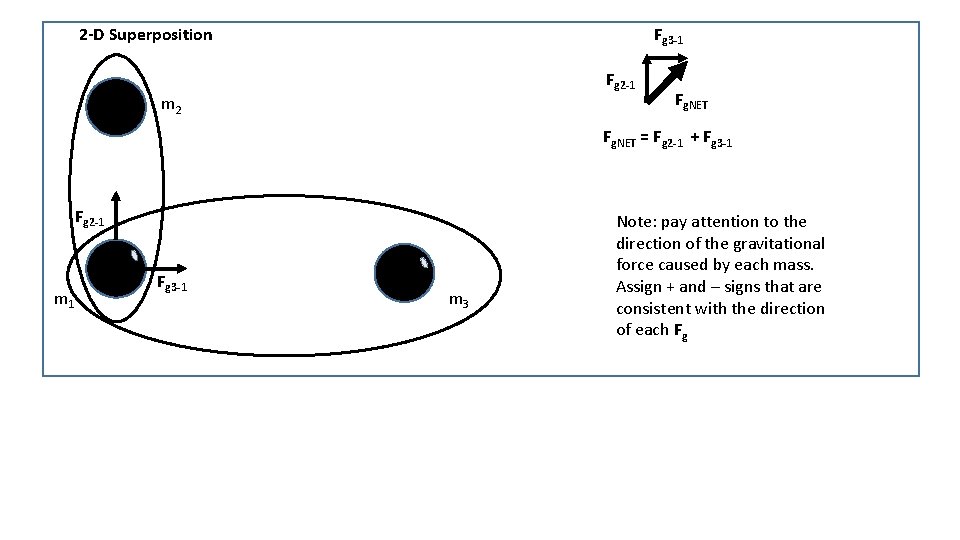
Fg 3 -1 2 -D Superposition Fg 2 -1 m 2 Fg. NET = Fg 2 -1 + Fg 3 -1 Fg 2 -1 m 1 Fg 3 -1 m 3 Note: pay attention to the direction of the gravitational force caused by each mass. Assign + and – signs that are consistent with the direction of each Fg

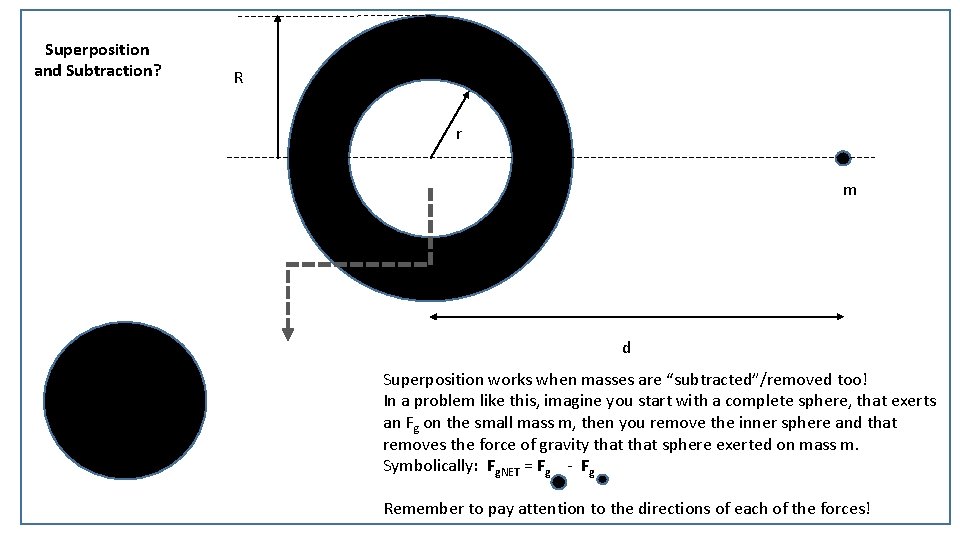
Superposition and Subtraction? R r m d Superposition works when masses are “subtracted”/removed too! In a problem like this, imagine you start with a complete sphere, that exerts an Fg on the small mass m, then you remove the inner sphere and that removes the force of gravity that sphere exerted on mass m. Symbolically: Fg. NET = Fg - Fg Remember to pay attention to the directions of each of the forces!

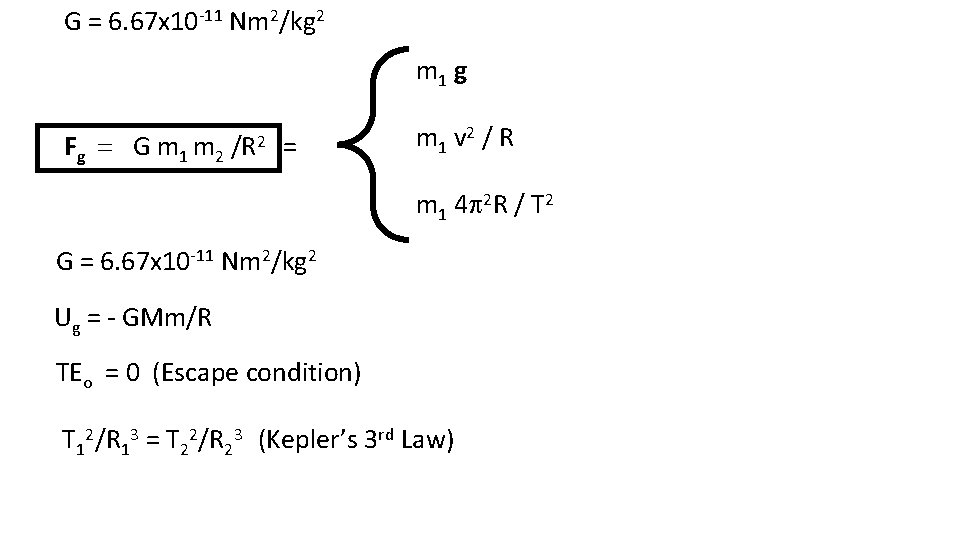
G = 6. 67 x 10 -11 Nm 2/kg 2 m 1 g Fg = G m 1 m 2 /R 2 = m 1 v 2 / R m 1 4 p 2 R / T 2 G = 6. 67 x 10 -11 Nm 2/kg 2 Ug = - GMm/R TEo = 0 (Escape condition) T 12/R 13 = T 22/R 23 (Kepler’s 3 rd Law)