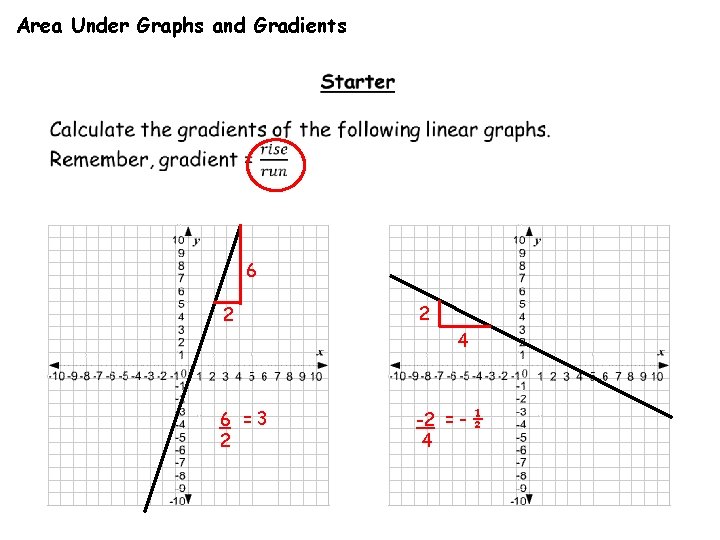
Area Under Graphs and Gradients 6 2 2

Area Under Graphs and Gradients 6 2 2 4 6 =3 2 -2 = - ½ 4

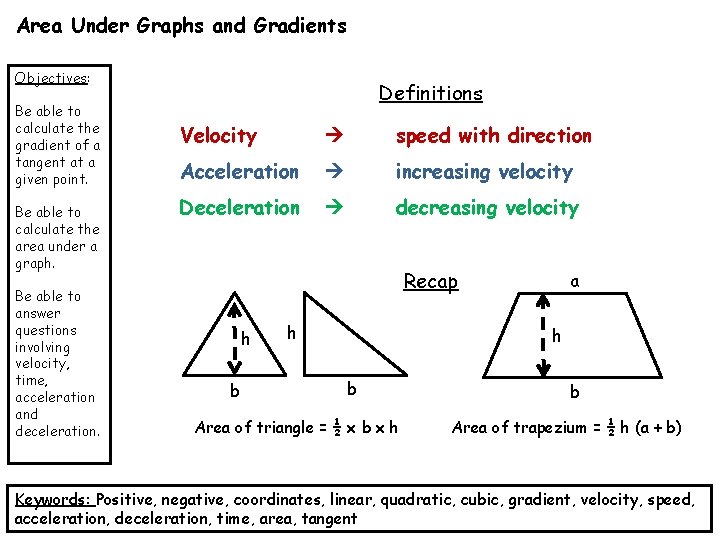
Area Under Graphs and Gradients Objectives: Be able to calculate the gradient of a tangent at a given point. Be able to calculate the area under a graph. Be able to answer questions involving velocity, time, acceleration and deceleration. Definitions Velocity speed with direction Acceleration increasing velocity Deceleration decreasing velocity Recap h b h a h b Area of triangle = ½ x b x h b Area of trapezium = ½ h (a + b) Keywords: Positive, negative, coordinates, linear, quadratic, cubic, gradient, velocity, speed, acceleration, deceleration, time, area, tangent

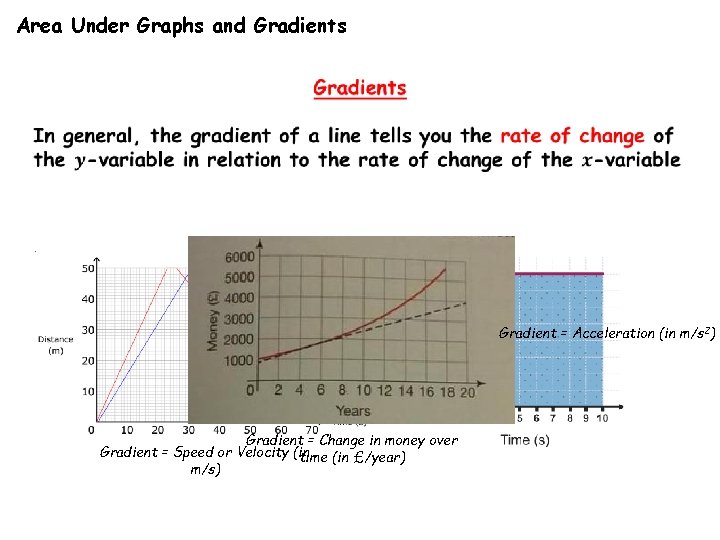
Area Under Graphs and Gradients Gradient = Acceleration (in m/s 2) Gradient = Change in money over Gradient = Speed or Velocity (in time (in £/year) m/s)

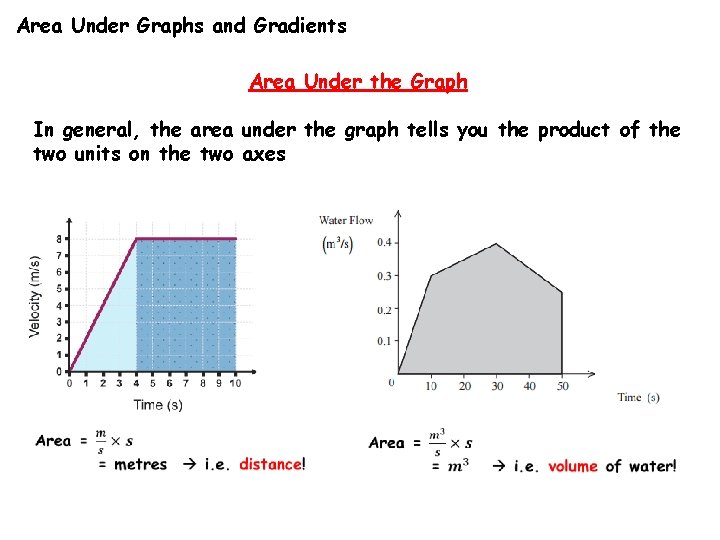
Area Under Graphs and Gradients Area Under the Graph In general, the area under the graph tells you the product of the two units on the two axes

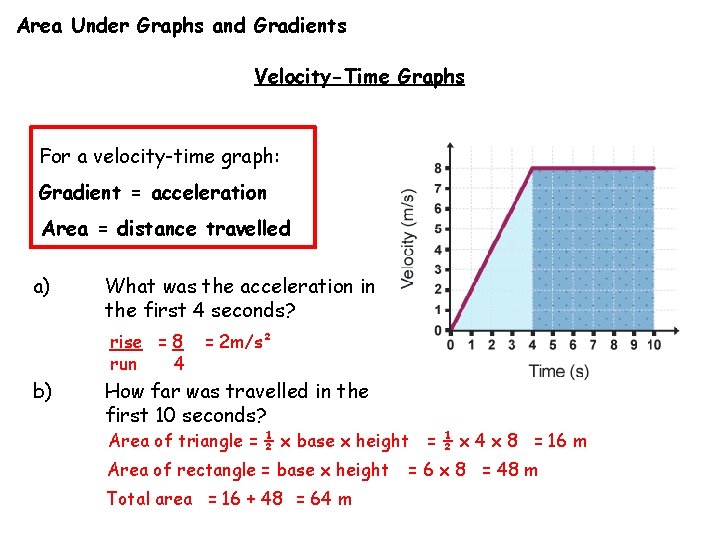
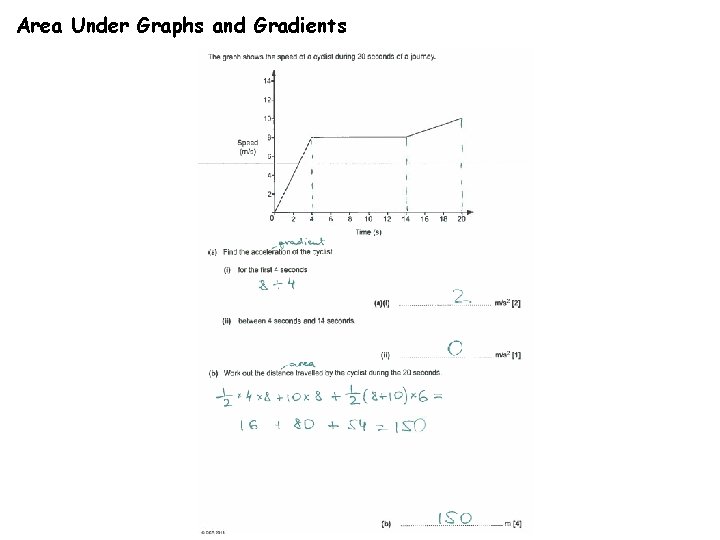
Area Under Graphs and Gradients Velocity-Time Graphs For a velocity-time graph: Gradient = acceleration Area = distance travelled a) What was the acceleration in the first 4 seconds? rise = 8 run 4 b) = 2 m/s² How far was travelled in the first 10 seconds? Area of triangle = ½ x base x height = ½ x 4 x 8 = 16 m Area of rectangle = base x height Total area = 16 + 48 = 64 m = 6 x 8 = 48 m

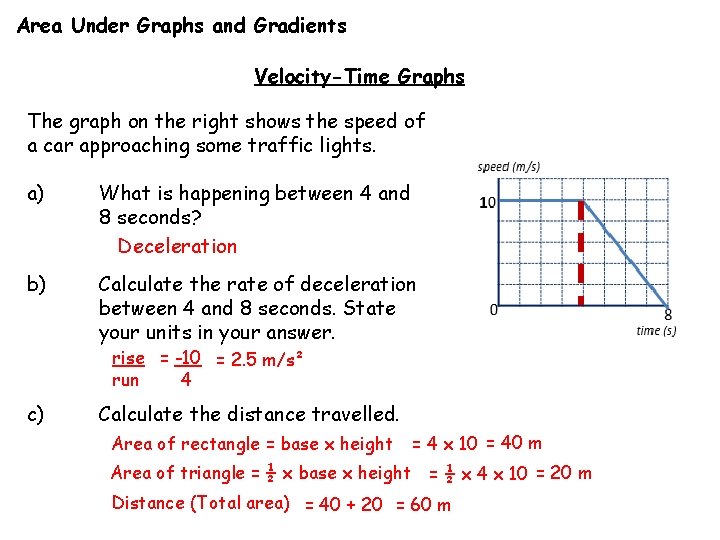
Area Under Graphs and Gradients Velocity-Time Graphs The graph on the right shows the speed of a car approaching some traffic lights. a) What is happening between 4 and 8 seconds? Deceleration b) Calculate the rate of deceleration between 4 and 8 seconds. State your units in your answer. rise = -10 = 2. 5 m/s² run 4 c) Calculate the distance travelled. Area of rectangle = base x height = 4 x 10 = 40 m Area of triangle = ½ x base x height = ½ x 4 x 10 = 20 m Distance (Total area) = 40 + 20 = 60 m

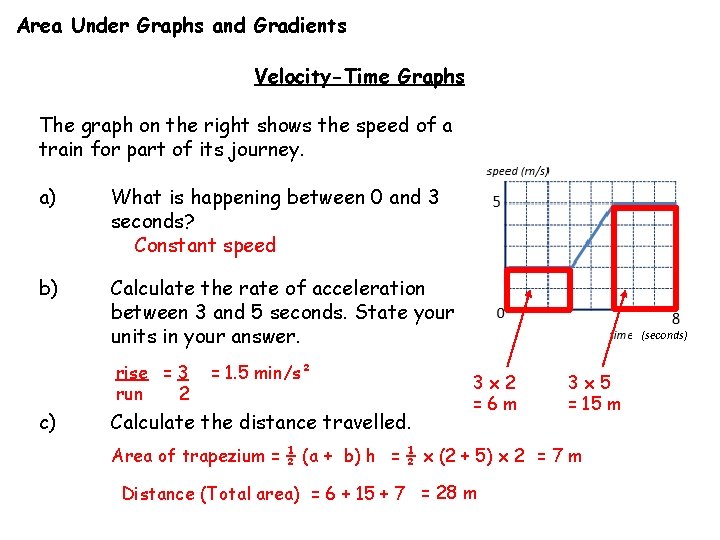
Area Under Graphs and Gradients Velocity-Time Graphs The graph on the right shows the speed of a train for part of its journey. a) What is happening between 0 and 3 seconds? Constant speed b) Calculate the rate of acceleration between 3 and 5 seconds. State your units in your answer. rise = 3 run 2 c) = 1. 5 min/s² Calculate the distance travelled. (seconds) 3 x 2 =6 m 3 x 5 = 15 m Area of trapezium = ½ (a + b) h = ½ x (2 + 5) x 2 = 7 m Distance (Total area) = 6 + 15 + 7 = 28 m

Area Under Graphs and Gradients Click on the link to watch Corbettmaths video clip, then return to the Power. Point presentation https: //www. youtube. com/watch? v=1 AVtsl. Xyt. RA

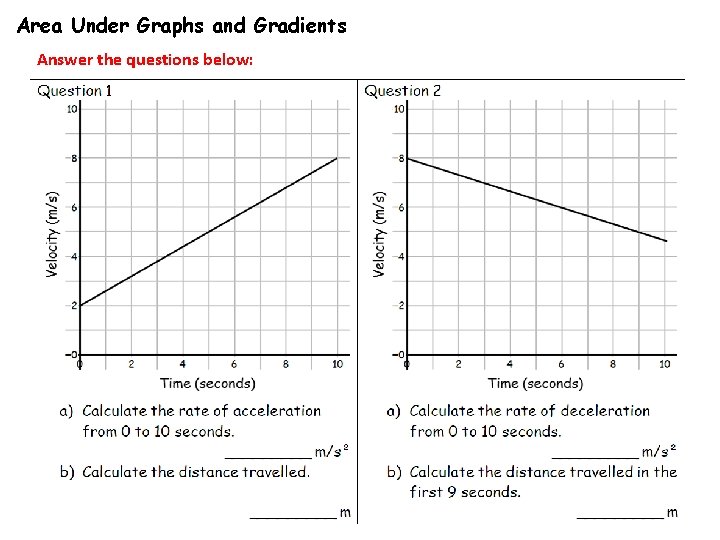
Area Under Graphs and Gradients Answer the questions below:

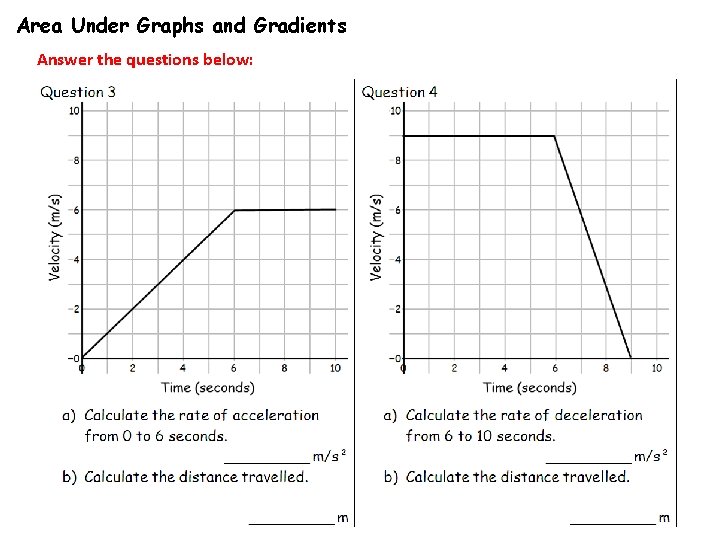
Area Under Graphs and Gradients Answer the questions below:

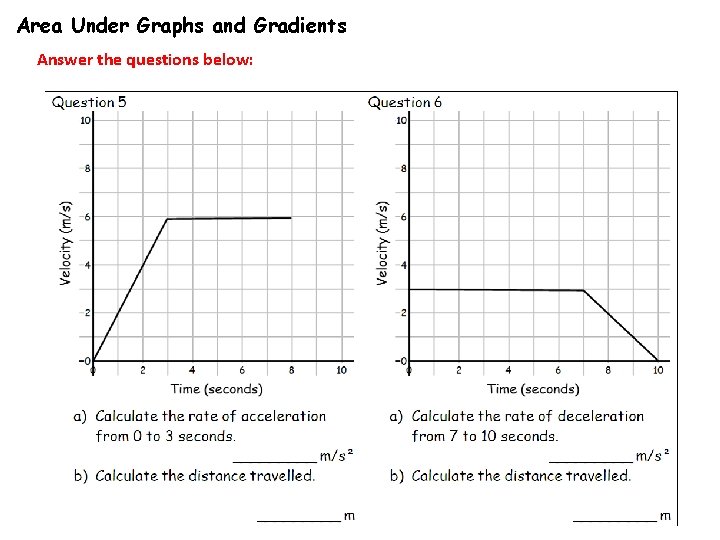
Area Under Graphs and Gradients Answer the questions below:

Area Under Graphs and Gradients Answers 1 a. b. 0. 6 m/s² 50 m 2 a. b. 0. 3 m/s² 58. 5 m 3 a. b. 1 m/s² 42 m 4 a. b. 3 m/s² 67. 5 m 5 a. b. 2 m/s² 39 m 6 a. b. 1 m/s² 25. 5 m

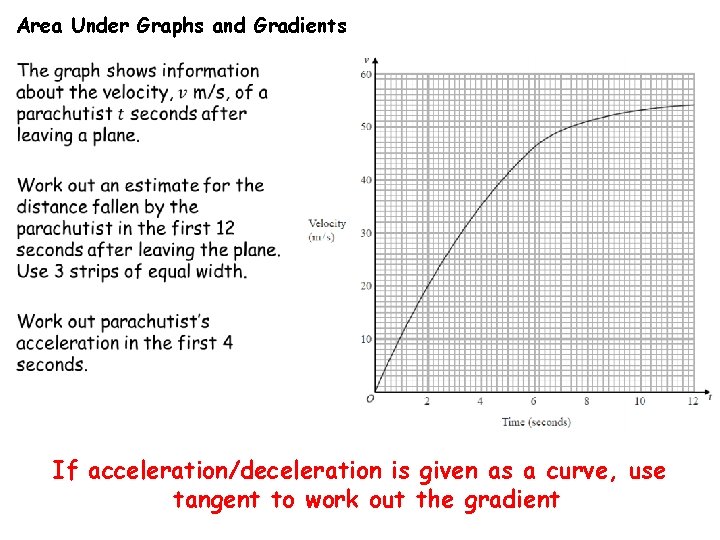
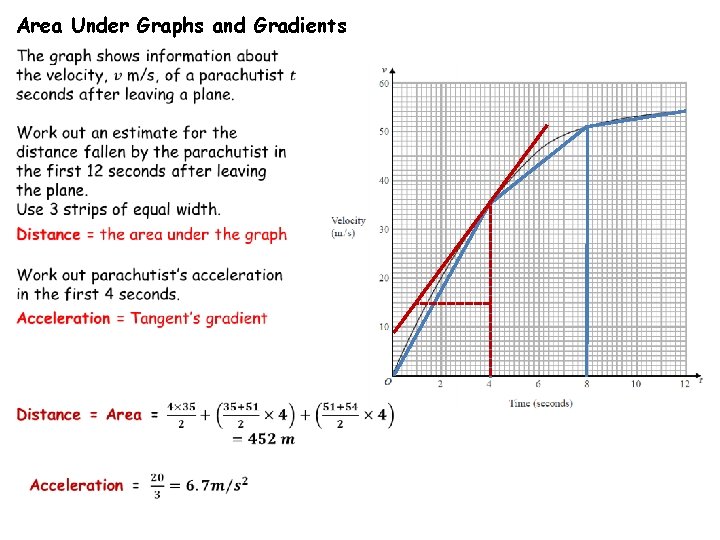
Area Under Graphs and Gradients If acceleration/deceleration is given as a curve, use tangent to work out the gradient

Area Under Graphs and Gradients

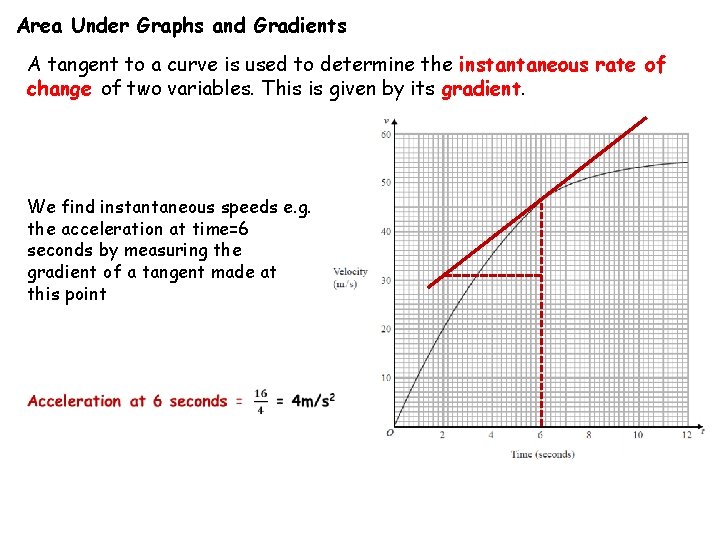
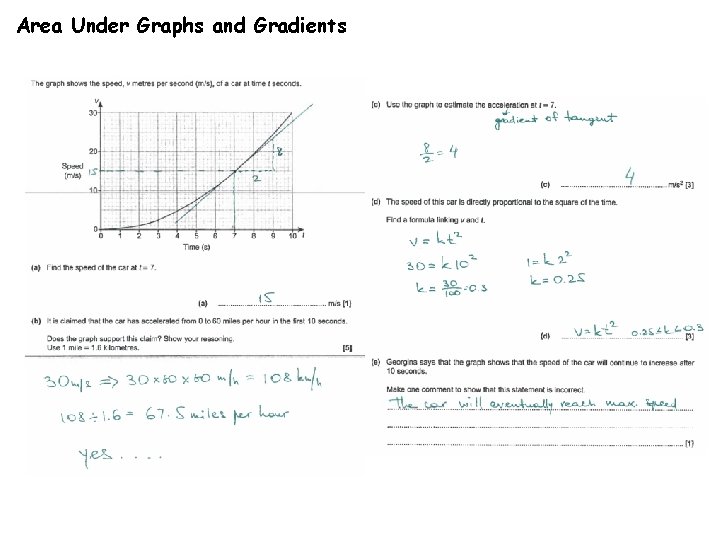
Area Under Graphs and Gradients A tangent to a curve is used to determine the instantaneous rate of change of two variables. This is given by its gradient. We find instantaneous speeds e. g. the acceleration at time=6 seconds by measuring the gradient of a tangent made at this point

Area Under Graphs and Gradients Now watch this clip, then return to the Power. Point presentation https: //www. youtube. com/watch? v=Yf. Dh. Gn 3 NLQw

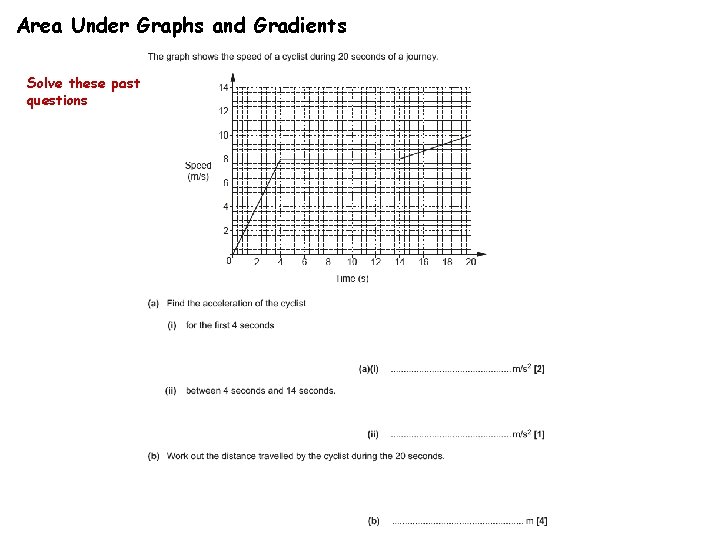
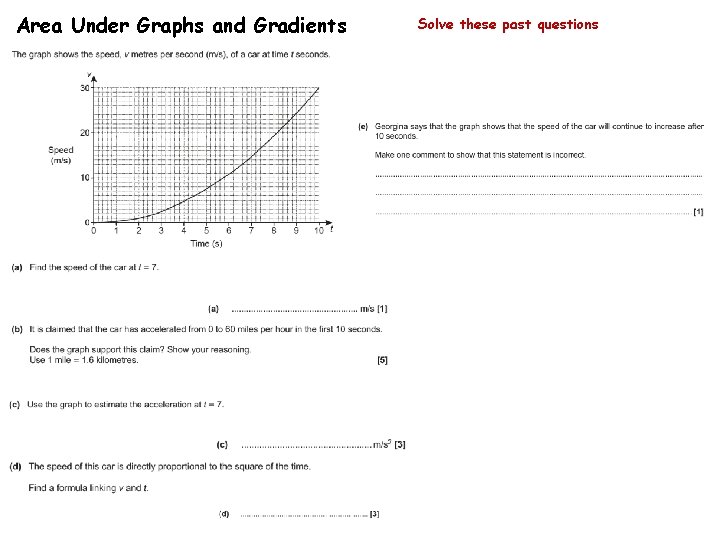
Area Under Graphs and Gradients Solve these past questions

Area Under Graphs and Gradients

Area Under Graphs and Gradients Solve these past questions

Area Under Graphs and Gradients

Area Under Graphs and Gradients For extra practice, please use the sample questions emailed with this presentation