AREA DELLESAGONO REGOLARE AREA DI ALTRI POLIGONI REGOLARI

AREA DELL’ESAGONO REGOLARE AREA DI ALTRI POLIGONI REGOLARI www. renatopatrignani. net

AREA DELL’ESAGONO REGOLARE www. renatopatrignani. net

APOTEMA DELL’ESAGONO REGOLARE a L’esagono regolare si può suddividere in 6 triangoli isosceli uguali, la cui altezza corrisponde all’apotema dell’esagono (cioè al raggio della circonferenza inscritta) www. renatopatrignani. net

RAPPORTO FRA APOTEMA E LATO In ogni esagono c’è sempre lo stesso rapporto fra apotema e lato Per questo motivo a : l = 0, 866 Perciò: Se si conosce il lato, si può calcolare l’apotema: a = l x 0, 866 Se si conosce l’apotema, si può calcolare il lato: l = a : 0, 866 a= 3 cm è il numero fisso dell’esagono X 0, 866 apotema lato l = 3, 464 cm : 0, 866 In questo esagono, a = 3 cm quindi: l = 3 : 0, 866 = 3, 464 www. renatopatrignani. net

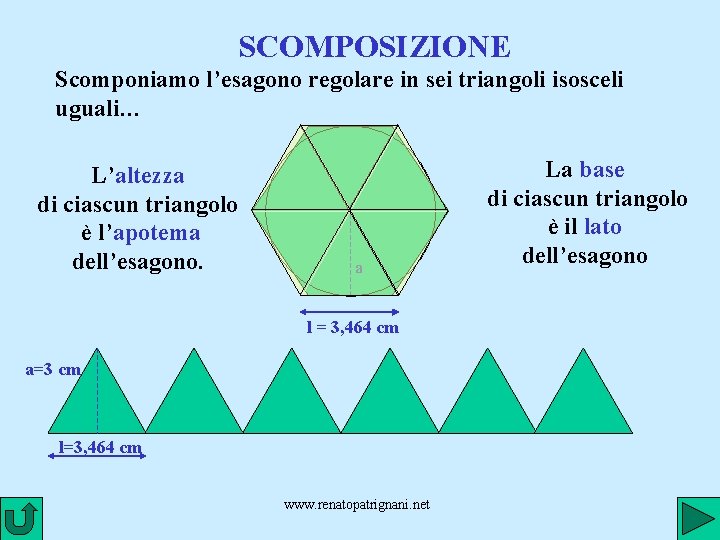
SCOMPOSIZIONE Scomponiamo l’esagono regolare in sei triangoli isosceli uguali… L’altezza di ciascun triangolo è l’apotema dell’esagono. a l = 3, 464 cm a=3 cm l=3, 464 cm www. renatopatrignani. net La base di ciascun triangolo è il lato dell’esagono

CALCOLO Calcoliamo l’area di uno dei triangoli e poi moltiplichiamola per 6 3 cm 4, 464 cm Applichiamo la formula dell’area del triangolo: A=bxh: 2 A = (4, 464 x 3): 2 = 6, 696 cm 2 (Area di uno dei triangoli) 6, 696 x 6 = 40, 176 cm 2 (Area dei sei triangoli e, quindi, dell’esagono) www. renatopatrignani. net

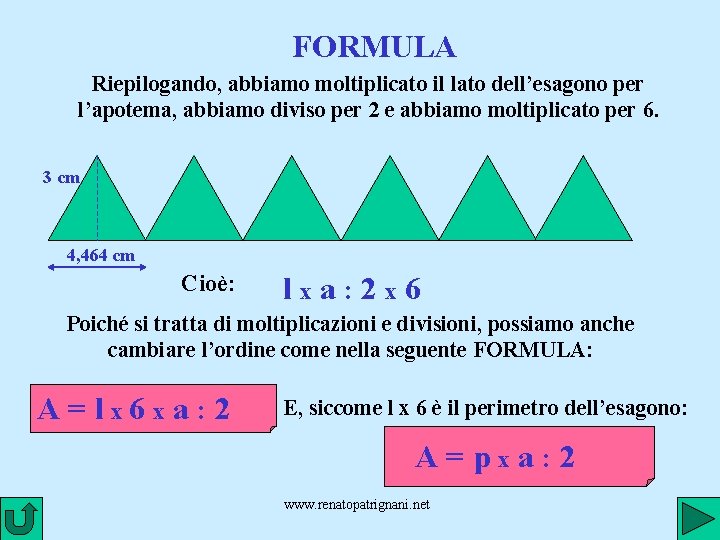
FORMULA Riepilogando, abbiamo moltiplicato il lato dell’esagono per l’apotema, abbiamo diviso per 2 e abbiamo moltiplicato per 6. 3 cm 4, 464 cm Cioè: lxa: 2 x 6 Poiché si tratta di moltiplicazioni e divisioni, possiamo anche cambiare l’ordine come nella seguente FORMULA: A = l x 6 x a : 2 E, siccome l x 6 è il perimetro dell’esagono: A=pxa: 2 www. renatopatrignani. net

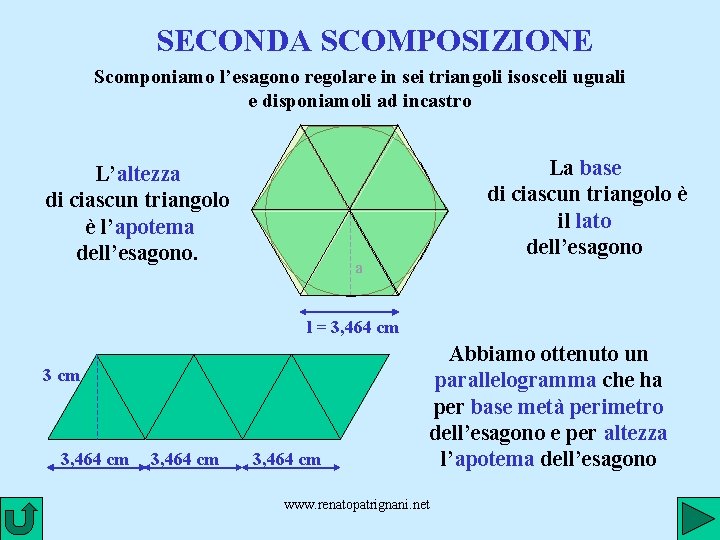
SECONDA SCOMPOSIZIONE Scomponiamo l’esagono regolare in sei triangoli isosceli uguali e disponiamoli ad incastro L’altezza di ciascun triangolo è l’apotema dell’esagono. La base di ciascun triangolo è il lato dell’esagono a l = 3, 464 cm 3, 464 cm Abbiamo ottenuto un parallelogramma che ha per base metà perimetro dell’esagono e per altezza l’apotema dell’esagono www. renatopatrignani. net

FORMULA 3 cm 3, 464 cm Per calcolare l’area del parallelogramma, che è anche area dell’esagono, moltiplichiamo la base (semiperimetro dell’esagono) per l’altezza (apotema dell’esagono). A=p: 2 xa Che è come dire: A=lx 6: 2 xa A = 3, 464 x 6 : 2 x 3 = 40, 196 cm 2 www. renatopatrignani. net

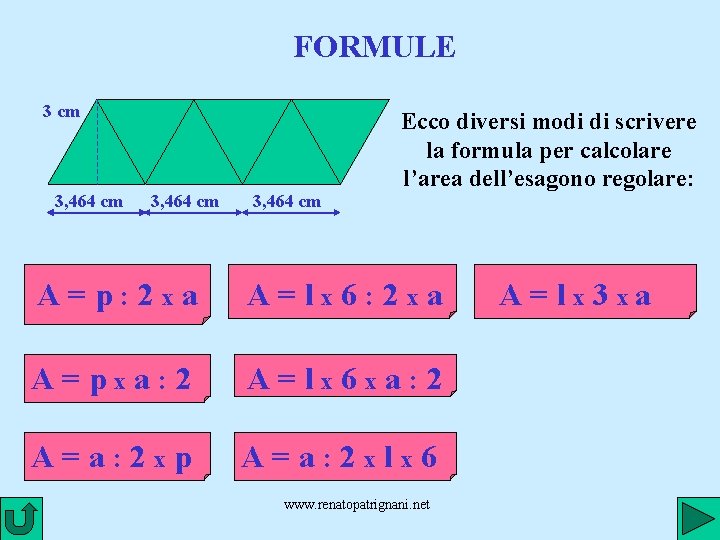
FORMULE 3 cm 3, 464 cm Ecco diversi modi di scrivere la formula per calcolare l’area dell’esagono regolare: A=p: 2 xa A=lx 6: 2 xa A=pxa: 2 A=lx 6 xa: 2 A=a: 2 xp A=a: 2 xlx 6 www. renatopatrignani. net A = l x 3 xa

AREA DI ALTRI POLIGONI REGOLARI www. renatopatrignani. net

SCOMPOSIZIONE DI POLIGONI REGOLARI Pentagono, ettagono, ottagono, ennagono, decagono, come l’esagono, si possono scomporre in tanti triangoli isosceli uguali quanti sono i loro lati. Perciò il modo di calcolare la loro area si differenzia soltanto per il numero dei triangoli in cui si scompongono. Ø PENTAGONO: 5 triangoli Ø ENNAGONO: 9 triangoli Ø ESAGONO; 6 triangoli Ø DECAGONO: 10 triangoli Ø ETTAGONO: 7 triangoli ØUNDECAGONO: 11 triangoli Ø OTTAGONO: 8 triangoli ØDODECAGONO: 12 triangoli E via continuando… www. renatopatrignani. net

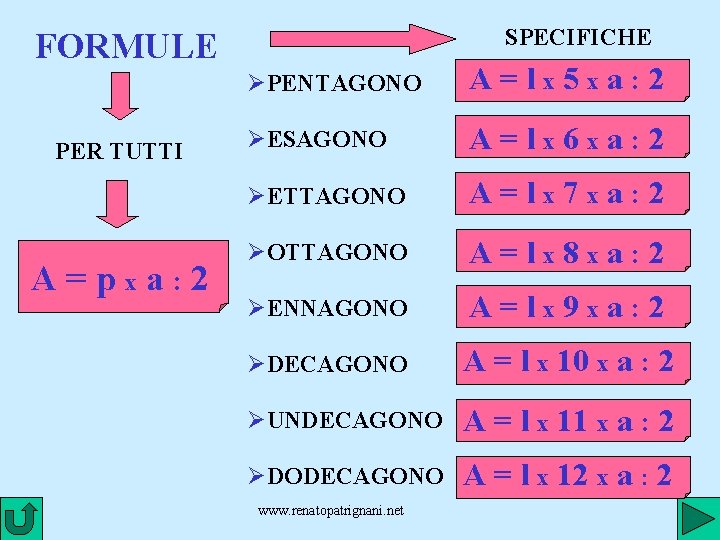
SPECIFICHE FORMULE PER TUTTI A=pxa: 2 ØPENTAGONO A=lx 5 xa: 2 ØESAGONO A=lx 6 xa: 2 ØETTAGONO A=lx 7 xa: 2 ØOTTAGONO A=lx 8 xa: 2 ØENNAGONO A=lx 9 xa: 2 ØDECAGONO A = l x 10 x a : 2 ØUNDECAGONO A = l x 11 x a : 2 ØDODECAGONO A = l x 12 x a : 2 www. renatopatrignani. net

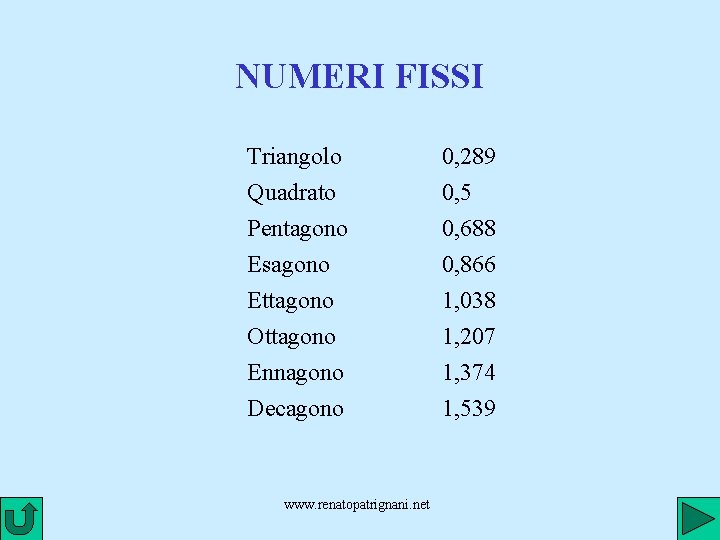
NUMERI FISSI Triangolo Quadrato Pentagono Esagono Ettagono 0, 289 0, 5 0, 688 0, 866 1, 038 Ottagono Ennagono Decagono 1, 207 1, 374 1, 539 www. renatopatrignani. net

F I N E www. renatopatrignani. net