Arcs and Sectors are Fractions of a Circle





- Slides: 14

Arcs and Sectors are Fractions of a Circle

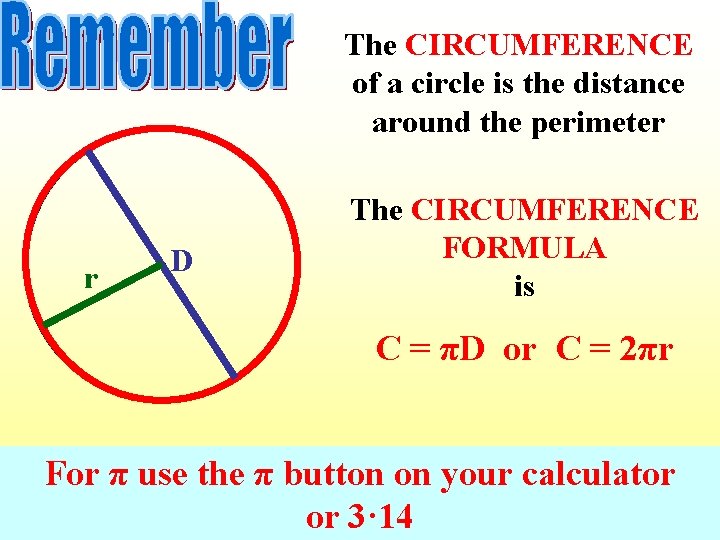
The CIRCUMFERENCE of a circle is the distance around the perimeter r • D The CIRCUMFERENCE FORMULA is C = πD or C = 2πr For π use the π button on your calculator or 3· 14

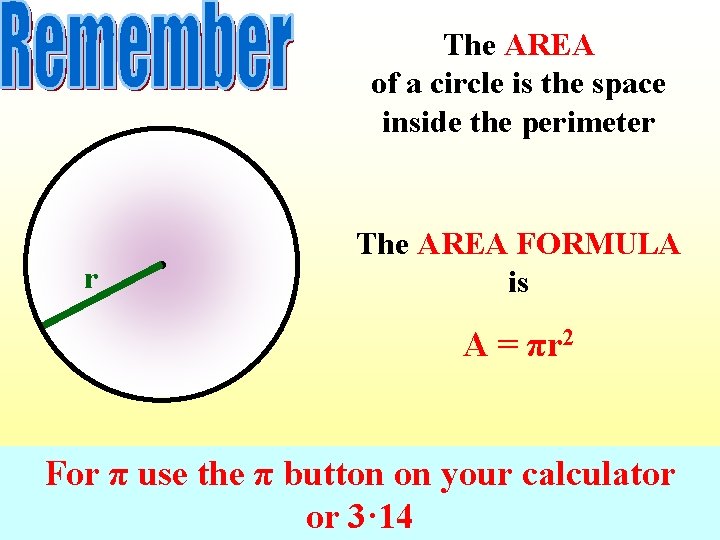
The AREA of a circle is the space inside the perimeter r • The AREA FORMULA is A = πr 2 For π use the π button on your calculator or 3· 14

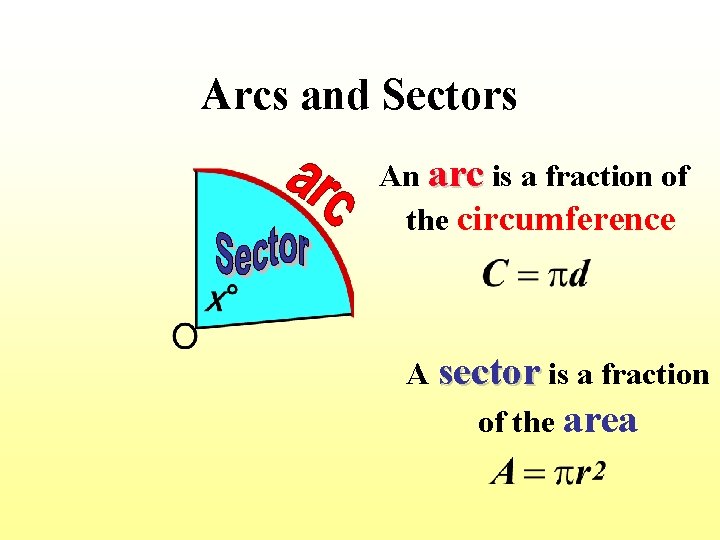
Arcs and Sectors An arc is a fraction of the circumference A sector is a fraction of the area

Finding the Fraction The fraction of the circle is a fraction A of 360° x° O B

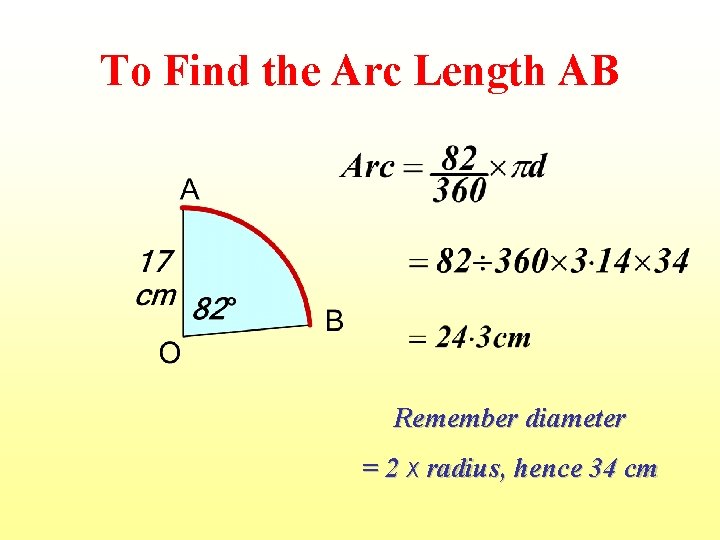
To Find the Arc Length AB Remember diameter = 2 x radius, hence 34 cm

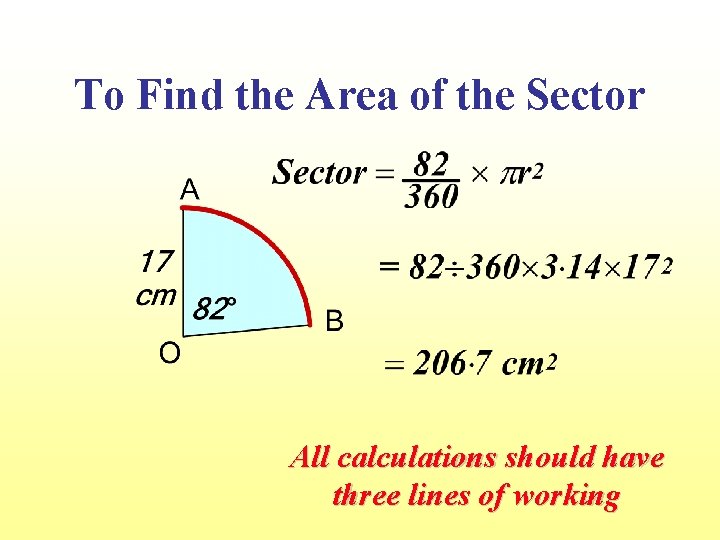
To Find the Area of the Sector All calculations should have three lines of working

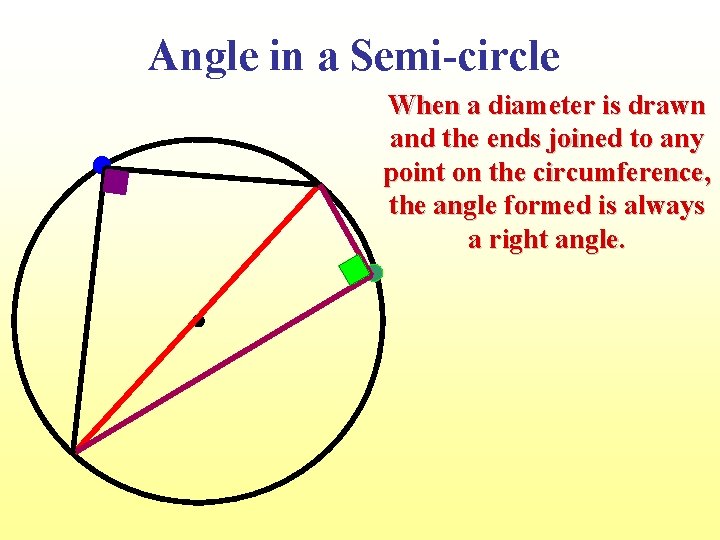
Angle in a Semi-circle When a diameter is drawn and the ends joined to any point on the circumference, the angle formed is always a right angle.

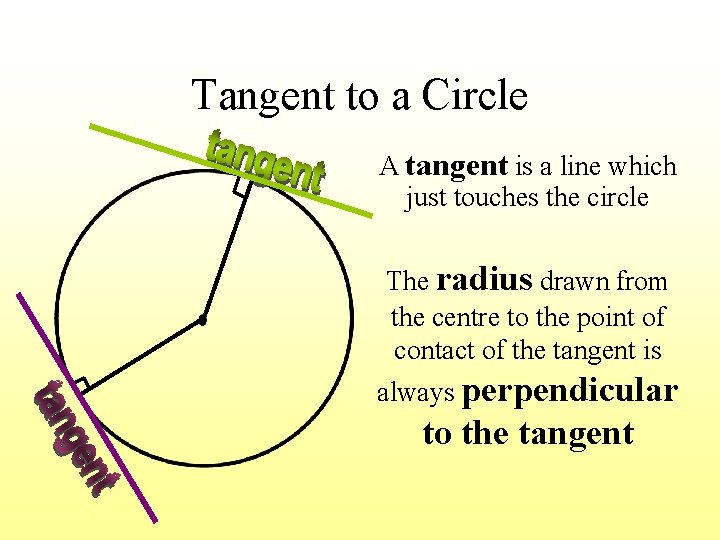
Tangent to a Circle A tangent is a line which just touches the circle The radius drawn from the centre to the point of contact of the tangent is always perpendicular to the tangent

Tangent Radius Problems Tangent radius problems involve right angled triangles: Sum of the angles in a triangle = 180° Pythagoras: a 2 = b 2 + c 2 SOH CAH TOA

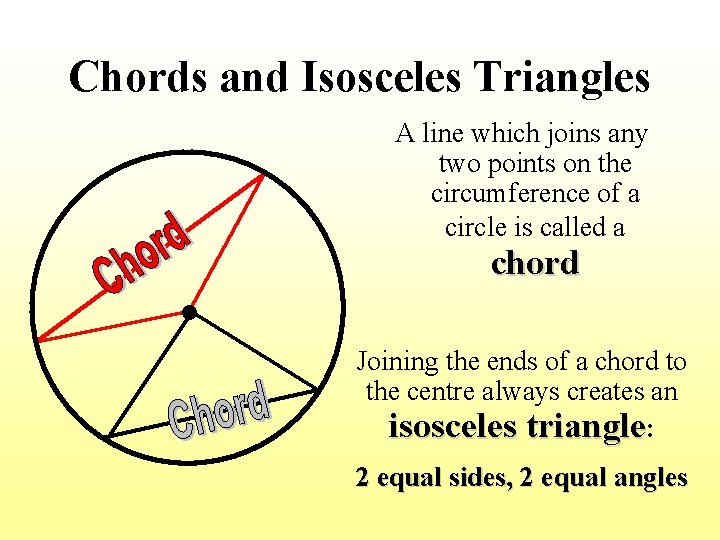
Chords and Isosceles Triangles A line which joins any two points on the circumference of a circle is called a • chord Joining the ends of a chord to the centre always creates an isosceles triangle: 2 equal sides, 2 equal angles

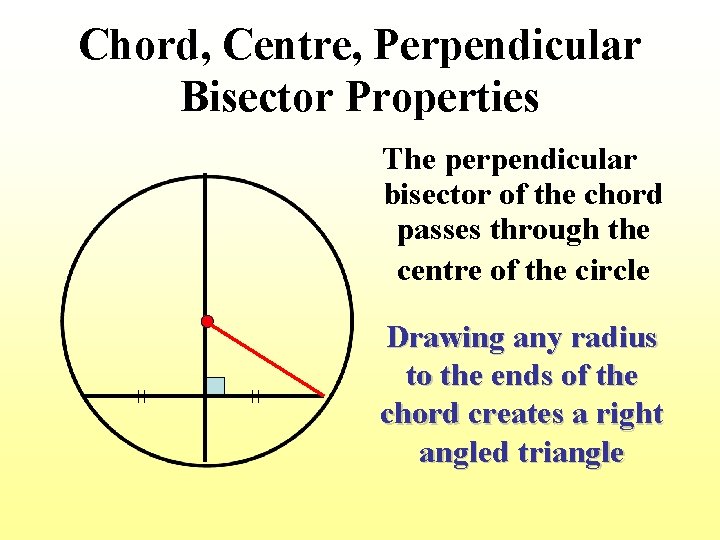
Chord, Centre, Perpendicular Bisector Properties The perpendicular bisector of the chord passes through the centre of the circle Drawing any radius to the ends of the chord creates a right angled triangle

Typical Perpendicular Bisector Problem The diagram shows a water pipe of radius 50 cm. The distance across the surface is 84 cm Calculate the depth of water in the pipe. Draw bisector and use Pythagoras in ∆OSQ to calculate OS O 14 cm P 50 cm S 42 cm R 84 cm Q Since OR is another radius, SR, the depth of water, is 50 - 14 = 36 cm

What I Should Know How to: find the length of an arc of a circle find the area of a sector of a circle How to use the properties of circles: relationship between tangent and radius angle in a semi-circle the interdependence of the centre, bisector of a chord and a perpendicular to a chord