Archimedean Solids By Alena and Wynne History of

Archimedean Solids By: Alena and Wynne

History of Archideas • He lived after Euclid • Worked in Syracuse which is a Mediterranean island of Sicily • 1 has a tetrahedral symmetry • 6 have cub-octahedral symmetry • 6 have icosa-dodecahedral

Types of Archimedean Solids Cuboctahedron • 6 squares • 8 equilateral triangles • 14 faces • 12 vertices • 24 edges

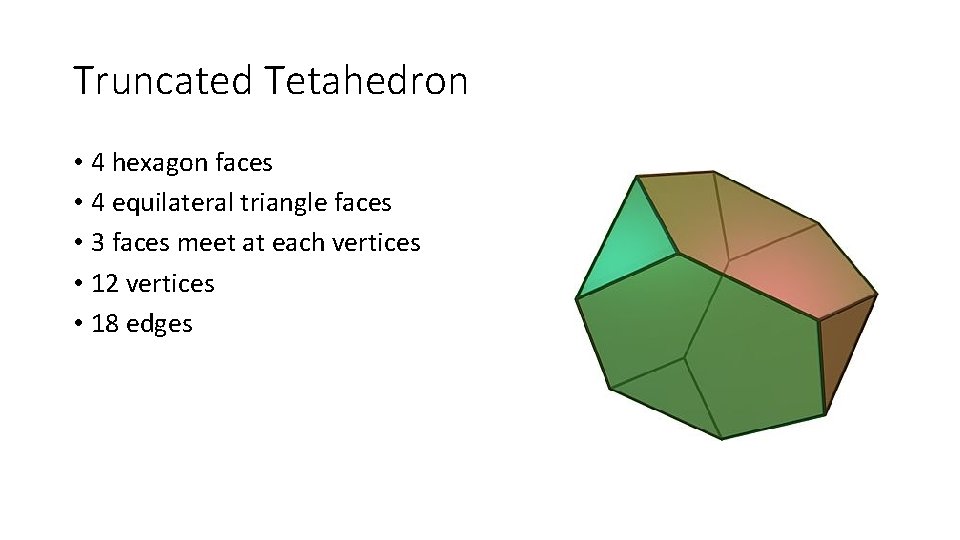
Truncated Tetahedron • 4 hexagon faces • 4 equilateral triangle faces • 3 faces meet at each vertices • 12 vertices • 18 edges

Great rhombicosi dodecahedron • 30 squares • 20 hexagons • 12 decagons • 62 faces • 120 vertices • 180 edges

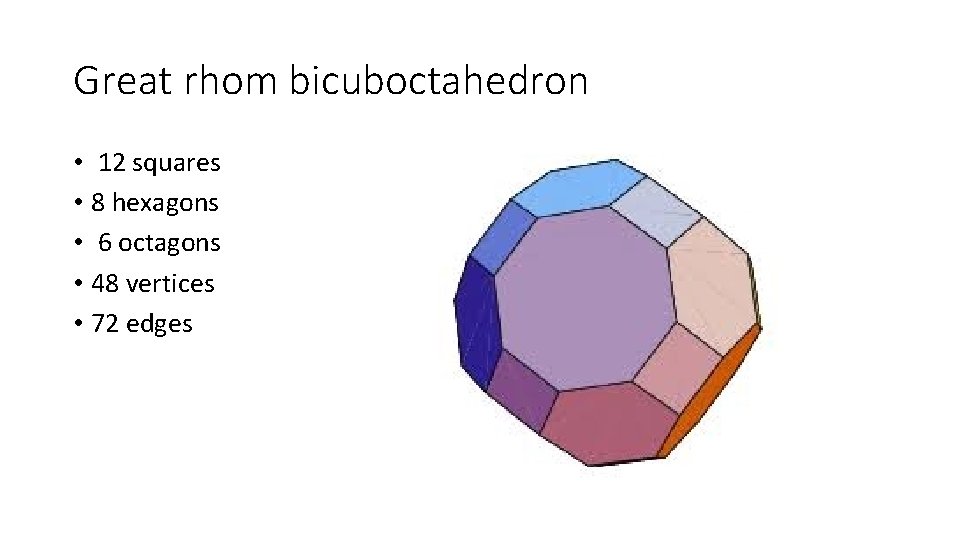
Great rhom bicuboctahedron • 12 squares • 8 hexagons • 6 octagons • 48 vertices • 72 edges

Icosidodecahedron • 20 triangles • 12 pentagons • 32 faces • 60 vertices • 90 edges

Small rhombicosi dodecahedron • 20 triangles • 30 squares • 12 pentagons • 60 vertices • 120 edges

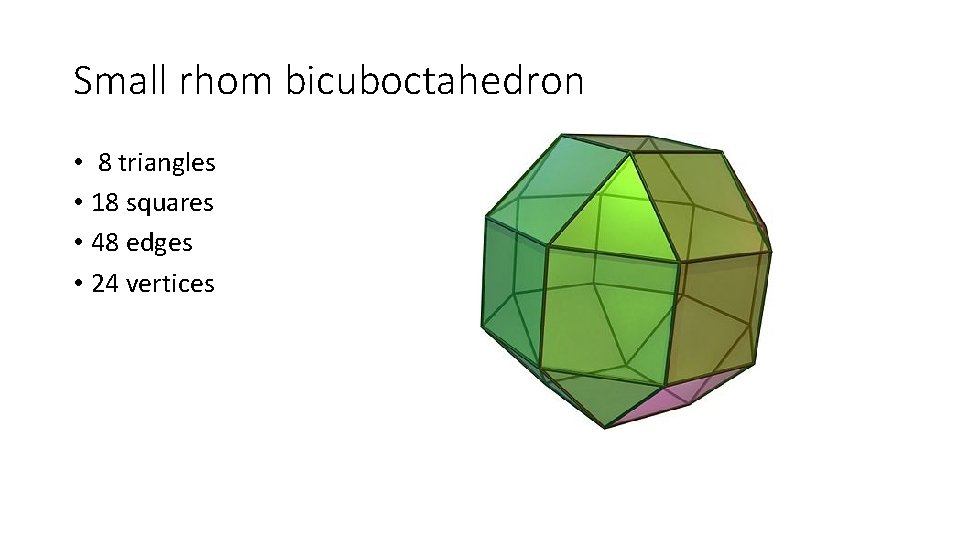
Small rhom bicuboctahedron • 8 triangles • 18 squares • 48 edges • 24 vertices

Snub cube • 32 triangles • 6 squares • 24 vertices • 60 edges • 38 faces

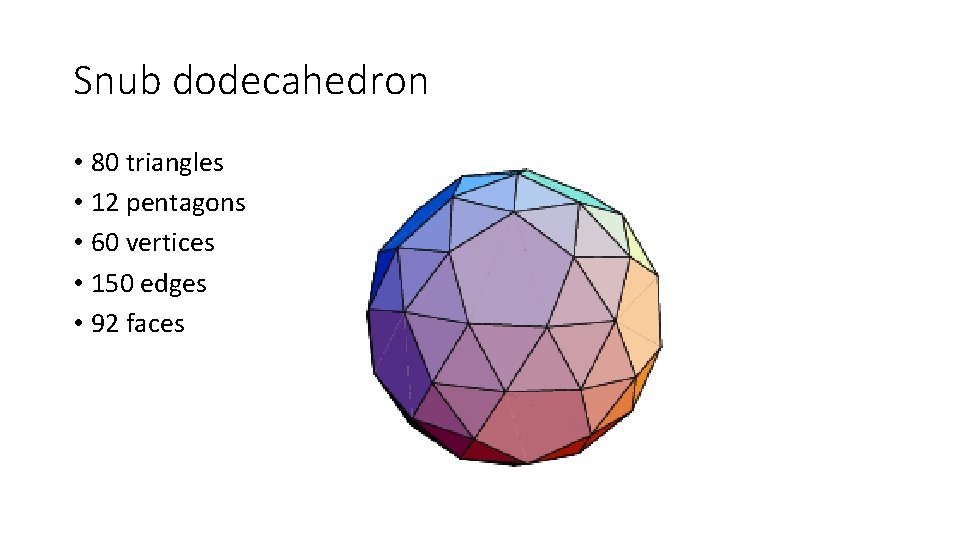
Snub dodecahedron • 80 triangles • 12 pentagons • 60 vertices • 150 edges • 92 faces

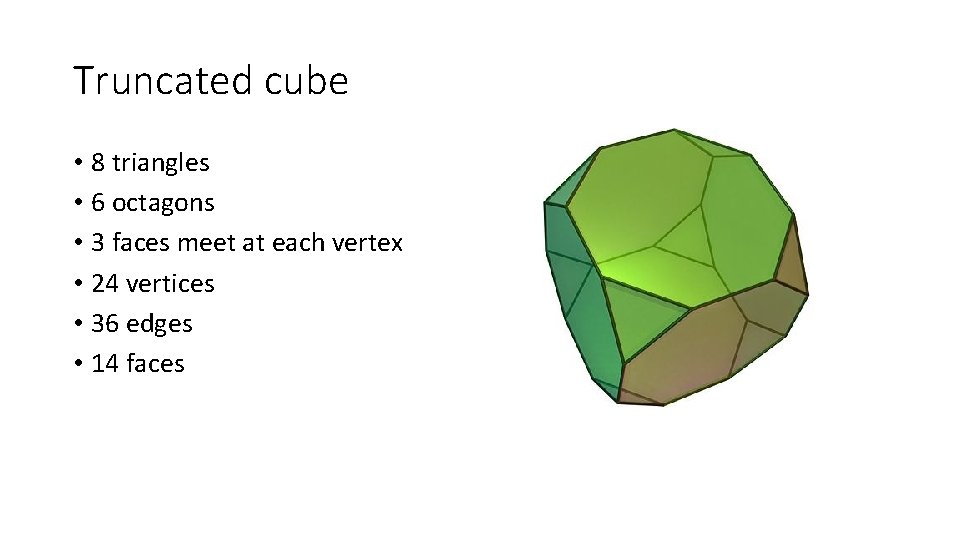
Truncated cube • 8 triangles • 6 octagons • 3 faces meet at each vertex • 24 vertices • 36 edges • 14 faces

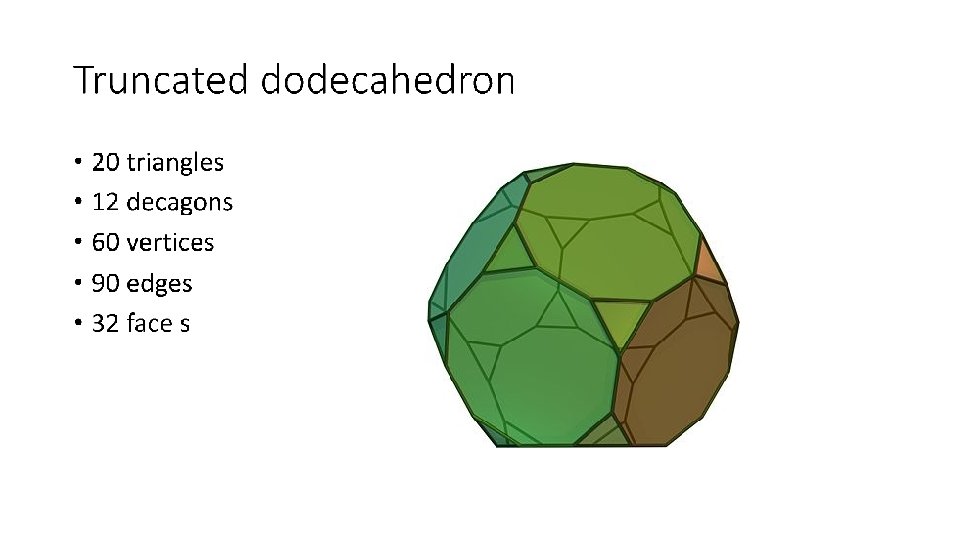
Truncated dodecahedron • 20 triangles • 12 decagons • 60 vertices • 90 edges • 32 face s

Truncated icosahedron • 12 pentagons • 20 hexagons • 60 vertices • 90 edges • 32 faces

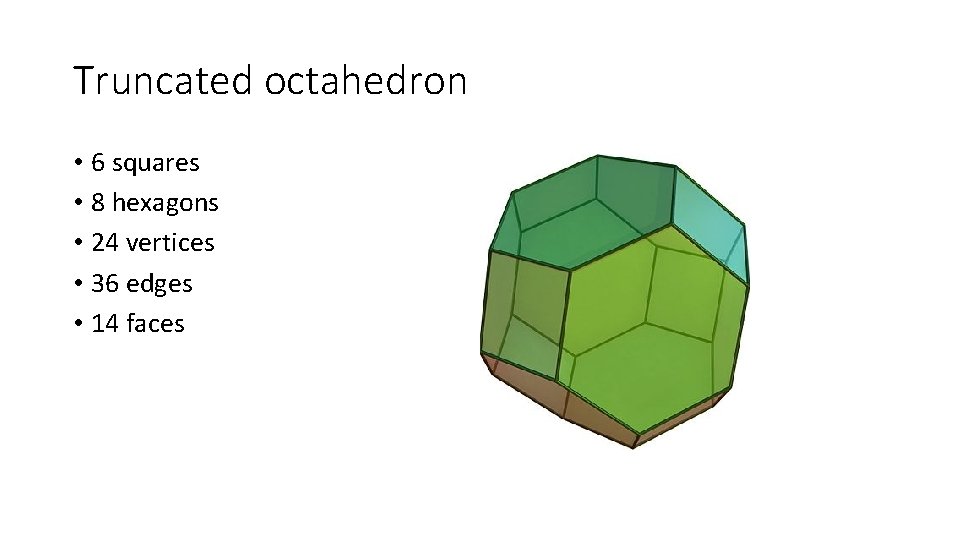
Truncated octahedron • 6 squares • 8 hexagons • 24 vertices • 36 edges • 14 faces

Similarities with each Archimedean solids • All solids have similar agreements of nonintersecting regular convex polygons • There are two or more different arranged shapes in the same way at each vertex with all sides with the same length • They are distinguished by having high symmetry, also called a dihedral group of symmetries and the elongated sqaure gryobicupola • Archimedean solids are referred to as semiregular polyhedral

Specific characteristics of solids • Seven of the thirteen solids can be obtained by truncation of a platonic solid, and they are: Cuboctahedron, Truncated cube, Truncated icosahedron, Truncated dodecahedron, Truncated octahedron, icosidodecahedron, and the truncated tetrahedron • The truncated cuboctahedron and the truncated icosidodecahedron need to be constructed by a different technique of being built from the original platonic solids which is called expansion. The faces need to be separated from the original polyhedron with spherical symmetry until they are linked with new faces which are regular polygons • The sub cube and dodecahedron have two special solids which have two chiral (specular symmetric) variations, and they can be treated as an alternation of another Archimedean solid. They are formed by getting rid of alternated vertices and making new triangles at the deleted vertices.

Connections • Archimedean solids are similar to platonic solids in the way that both forms of solids are formed by regular polygons. Meanwhile some of the Archimedean solids are formed from breaking apart the vertics in the platonic solid. They are both 3 D solids.

Sources • https: //en. wikipedia. org/wiki/Cuboctahedron • https: //en. wikipedia. org/wiki/Truncated_tetrahedron • http: //mathworld. wolfram. com/Great. Rhombicosidodecahedron. html • http: //mathworld. wolfram. com/Great. Rhombicuboctahedron. html • https: //en. wikipedia. org/wiki/Icosidodecahedron • https: //en. wikipedia. org/wiki/Rhombicuboctahedron • http: //mathworld. wolfram. com/Snub. Cube. html • http: //mathworld. wolfram. com/Snub. Dodecahedron. html • https: //en. wikipedia. org/wiki/Truncated_cube • https: //en. wikipedia. org/wiki/Truncated_dodecahedron • http: //mathworld. wolfram. com/Truncated. Icosahedron. html • https: //en. wikipedia. org/wiki/Truncated_octahedron • http: //mathworld. wolfram. com/Archimedean. Solid. html • http: //www. mathematische-basteleien. de/cuboctahedron. htm • https: //www. sacred-geometry. es/? q=en/content/archimedean-solids • http: //www. geom. uiuc. edu/~sudzi/polyhedra/archimedean. html • https: //digitalcommons. unl. edu/cgi/viewcontent. cgi? article=1003&context=mathmidexppap • https: //calculus 7. org/2012/09/06/archimedean-and-catalan-solids-picking-favorites/ • https: //americanhistory. si. edu/collections/object-groups/geometric-models/archimedean-solids-prisms-and-antiprisms

References • Anderson, A. (2008). 13 Archimedean Solids. Unpublished manuscript, University of Nebraska, Lincoln, USA. • Archimedean and Catalan solids: picking favorites. (2012, April 6). Retrieved April 15, 2019, from Calculus VII website: https: //calculus 7. org/2012/09/06/archimedean-and-catalan-solids-picking-favorites/ • Archimedean Solids. (n. d. ). Retrieved April 15, 2019, from Sacred Geometry website: https: //www. sacredgeometry. es/? q=en/content/archimedean-solids • Archimedean Solids, Prisms, and Antiprisms. (n. d. ). Retrieved April 15, 2019, from Smithsonian website: https: //americanhistory. si. edu/collections/object-groups/geometric-models/archimedean-solids-prisms-and-antiprisms • Cuboctahedron. (n. d. ). Retrieved April 15, 2019, from http: //www. mathematische-basteleien. de/cuboctahedron. htm • The 13 Archimedean Solids. (n. d. ). Retrieved April 15, 2019, from http: //www. geom. uiuc. edu/~sudzi/polyhedra/archimedean. html • Timmes, F. (n. d. ). Geometry of Art and Nature. Unpublished manuscript, School of the Art Institute of Chicago, USA. • Weisstein, E. W. (n. d. ). Archimedean Solids. Retrieved April 15, 2019, from Wolfram Math World website: http: //mathworld. wolfram. com/topics/Archimedean. Solids. html