Arc Length Cartesian Parametric and Polar Arc Length











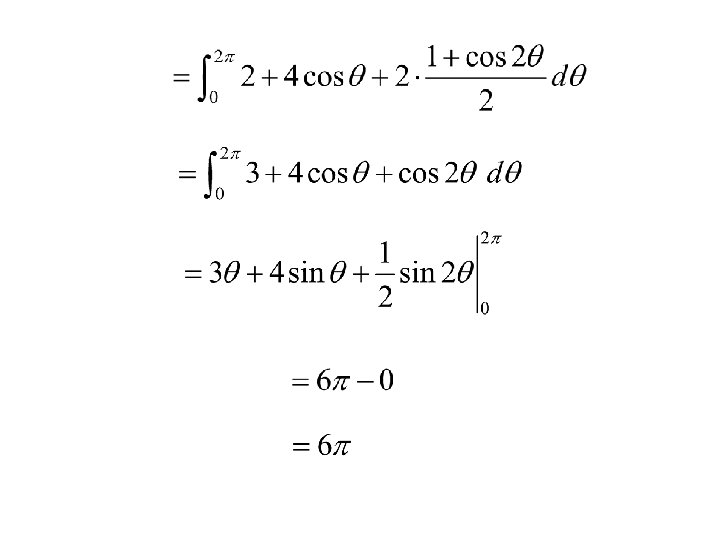

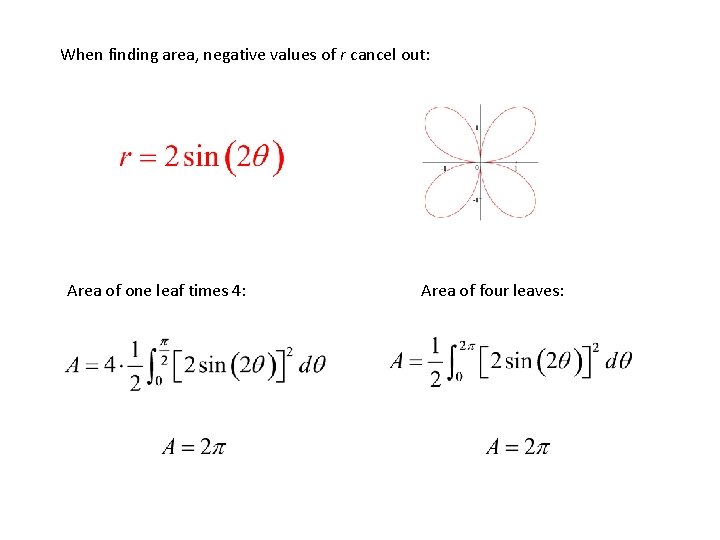


- Slides: 19

Arc Length Cartesian, Parametric, and Polar

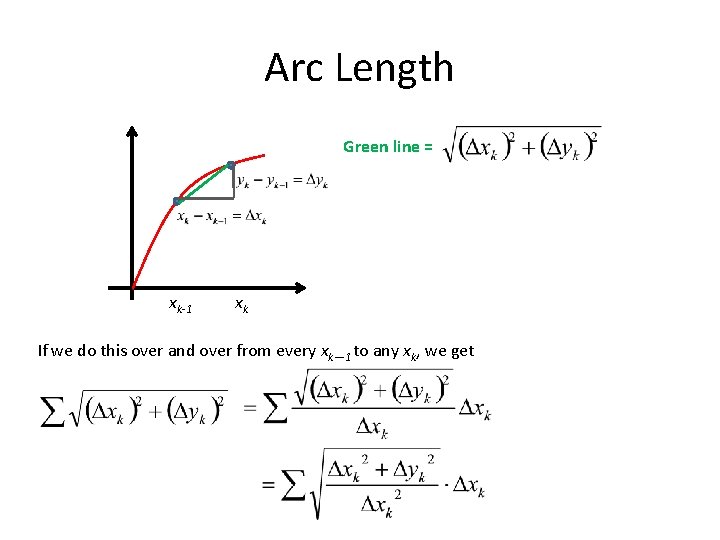
Arc Length Green line = xk-1 xk If we do this over and over from every xk— 1 to any xk, we get

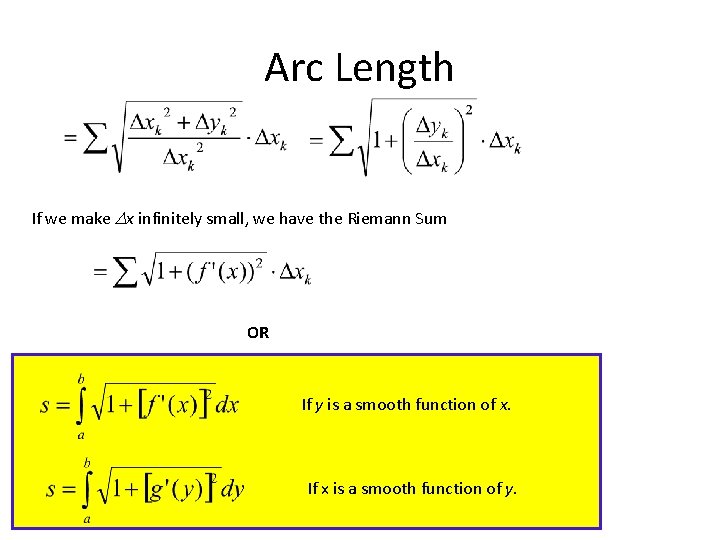
Arc Length If we make x infinitely small, we have the Riemann Sum OR If y is a smooth function of x. If x is a smooth function of y.

Arc Length • Example: Without a calculator, find the arc length of the curve for 0 x 1.

Arc Length • Find the length of the curve x = 8 and x = 8. between Since y is NOT DIFFERENTIABLE between – 8 and 8, we must use x in terms of y. f. Int

Surface Area • The surface area of a solid of revolution depends on the radius (the distance between the graph and the axis of revolution) and the arc length.

Surface Area • Find the area of the surface formed by revolving the graph of on the interval [0, 1] about the x-axis. Use u-sub.

Surface Area • Find the area of the surface formed by revolving the graph of f(x) = x 2 on the interval about the y-axis. In this case, the r(x) is x since the axis of revolution is the y-axis.

The equation for the length of a parametrized curve is similar to our previous “length of curve” equation: (Notice the use of the Pythagorean Theorem. ) (proof on pg. 721)

Parametric Arc Length • A circle of radius 1 rolls around the circumference of a larger circle of radius 4. The epicycloid traced by a point on the circumference of the smaller circle is given by and Find the distance traveled by the point in one complete trip about the larger circle.

Likewise, the equations for the surface area of a parametrized curve are similar to our previous “surface area” equations:

Area Inside a Polar Graph: The length of an arc (in a circle) is given by r. q when q is given in radians. For a very small q, the curve could be approximated by a straight line and the area could be found using the triangle formula:

We can use this to find the area inside a polar graph.

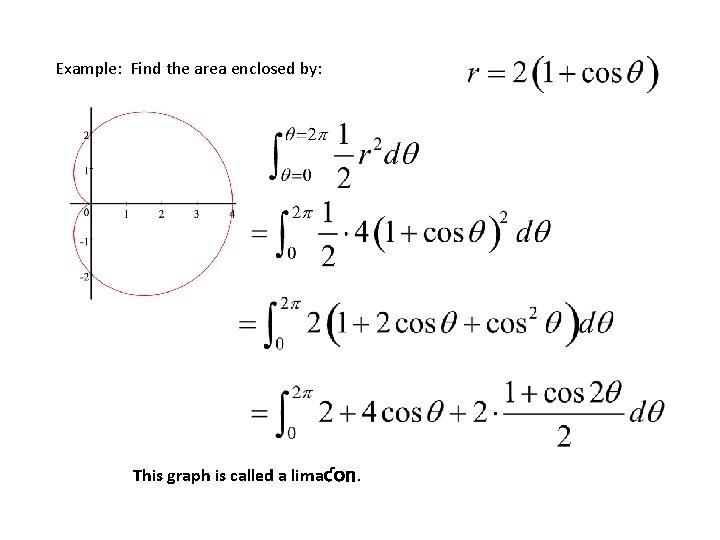
Example: Find the area enclosed by: This graph is called a limaƈon.
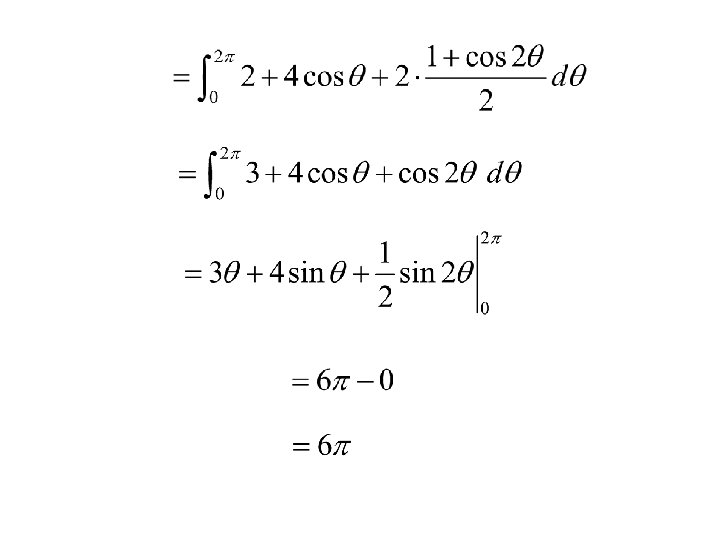

Notes: To find the area between curves, subtract: Just like finding the areas between Cartesian curves, establish limits of integration where the curves cross.
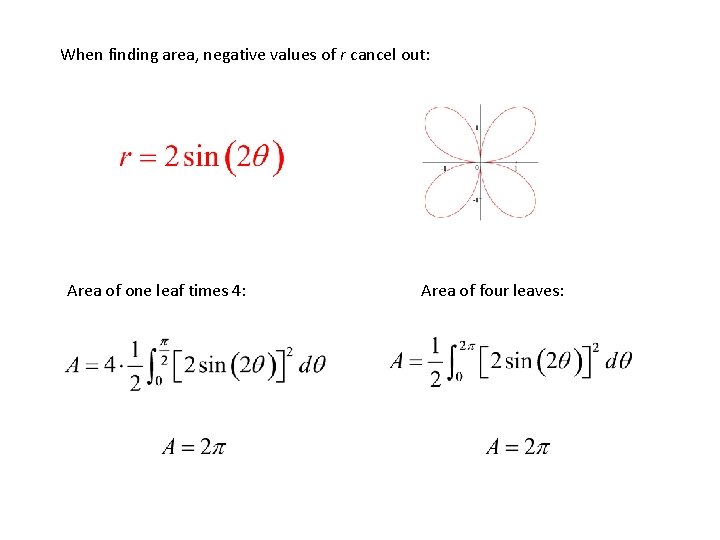
When finding area, negative values of r cancel out: Area of one leaf times 4: Area of four leaves:

To find the length of a curve: Remember: Again, for polar graphs: If we find derivatives and plug them into the formula, we (eventually) get: So:

There is also a surface area equation similar to the others we are already familiar with: When rotated about the x-axis: