Arbre Couvrants de Poids Minimum Coloration de graphes

Arbre Couvrants de Poids Minimum Coloration de graphes Par Francisco-Pierre Puig Slides originaux de Stanislas « Over » Plessia et Aymeric « Bebert » Bernard

Arbre Couvrant de Poids Minimal (Minimum Spanning Tree)

Définition et propriétés Prenons un graphe pondéré: Notre but est de relier tout les sommets, avec un arbre (donc sans aucun cycle) composé a partir d’arêtes du graphe. Cet arbre « couvrant » devant être minimal, l’objectif est de trouver un arbre dont le poids est minimisé par rapport à tout les arbres couvrants possibles.

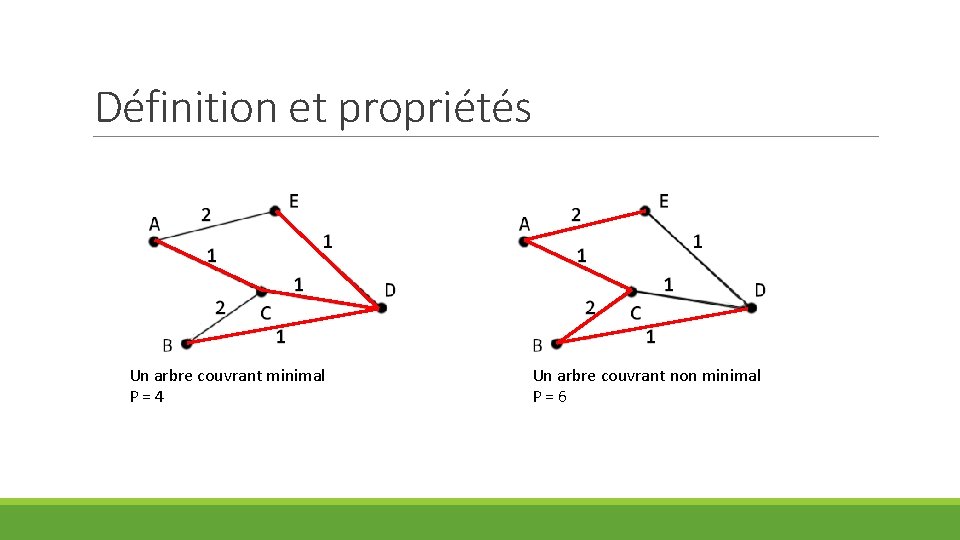
Définition et propriétés Un arbre couvrant minimal P=4 Un arbre couvrant non minimal P=6

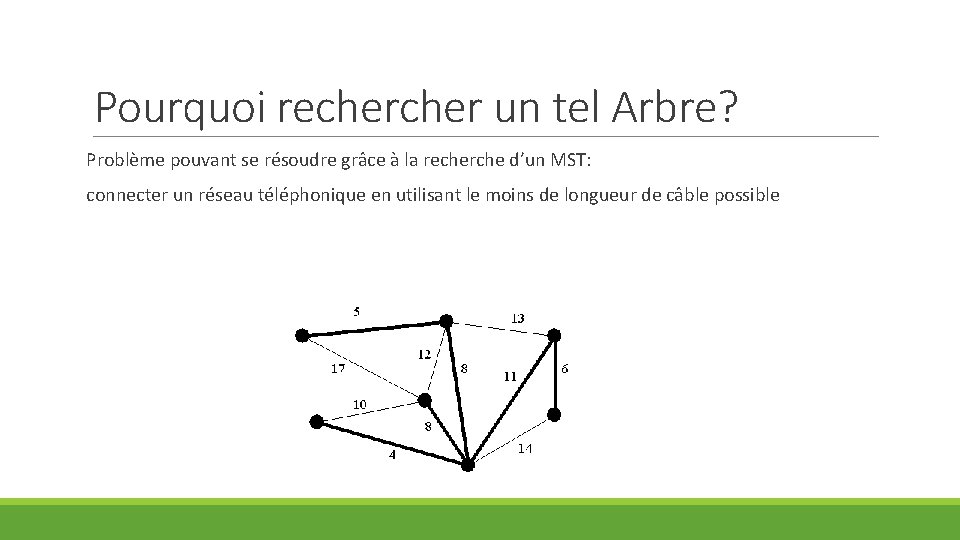
Pourquoi recher un tel Arbre? Problème pouvant se résoudre grâce à la recherche d’un MST: connecter un réseau téléphonique en utilisant le moins de longueur de câble possible

Algorithme de Prim Un premier algorithme pour cher de tels arbres est l’algorithme de Prim du nom de son auteur Robert C. Prim. C’est un algorithme glouton qui garantit de toujours donner une solution optimale (donc un arbre couvrant minimal). Principe: • On choisit un sommet de départ et on l’ajoute dans la liste des sommets atteints • A chaque étape, on ajoute l’arête de plus faible poids connectée à un sommet déjà atteint et qui permet d’atteindre un nouveau sommet • On s’arrête quand on a atteint tous les sommets

Algorithme de Prim Pseudo-Code :

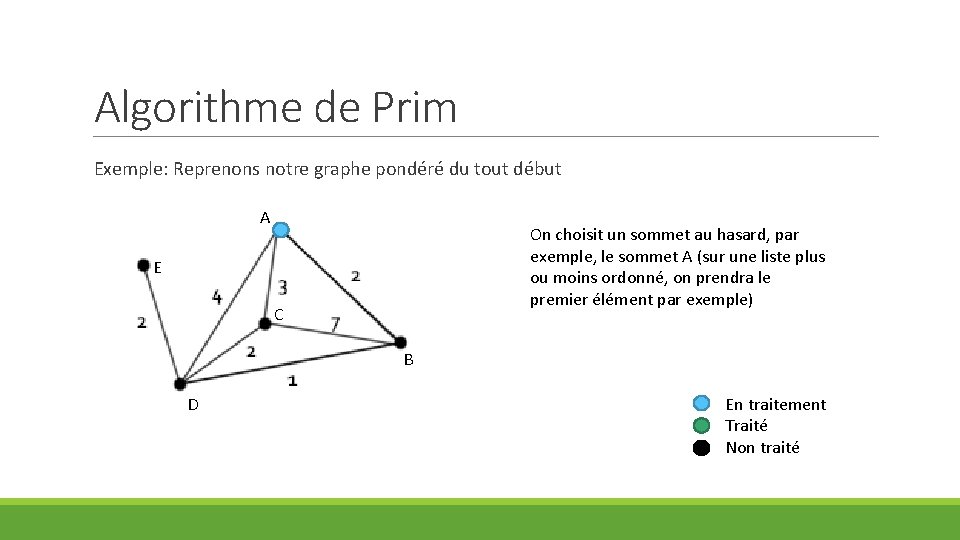
Algorithme de Prim Exemple: Reprenons notre graphe pondéré du tout début A On choisit un sommet au hasard, par exemple, le sommet A (sur une liste plus ou moins ordonné, on prendra le premier élément par exemple) E C B D En traitement Traité Non traité

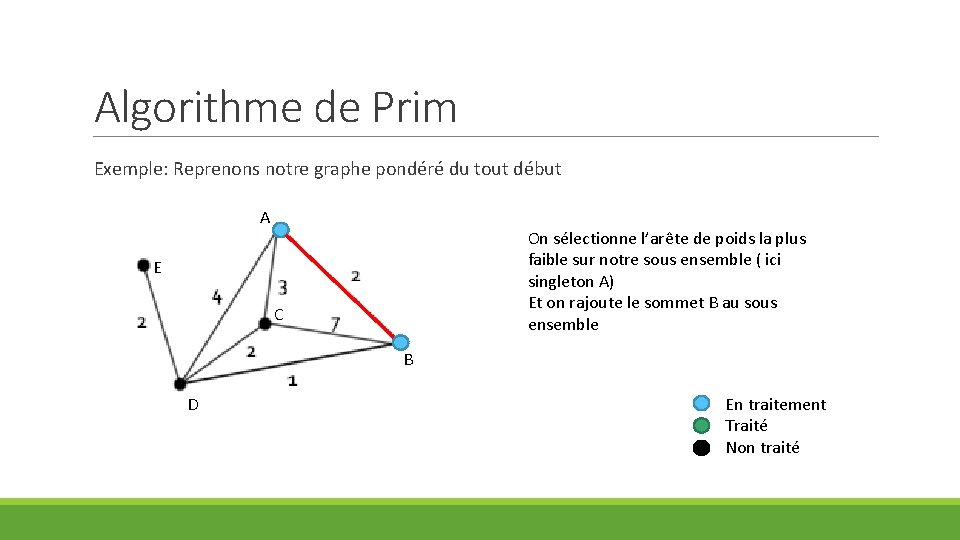
Algorithme de Prim Exemple: Reprenons notre graphe pondéré du tout début A On sélectionne l’arête de poids la plus faible sur notre sous ensemble ( ici singleton A) Et on rajoute le sommet B au sous ensemble E C B D En traitement Traité Non traité

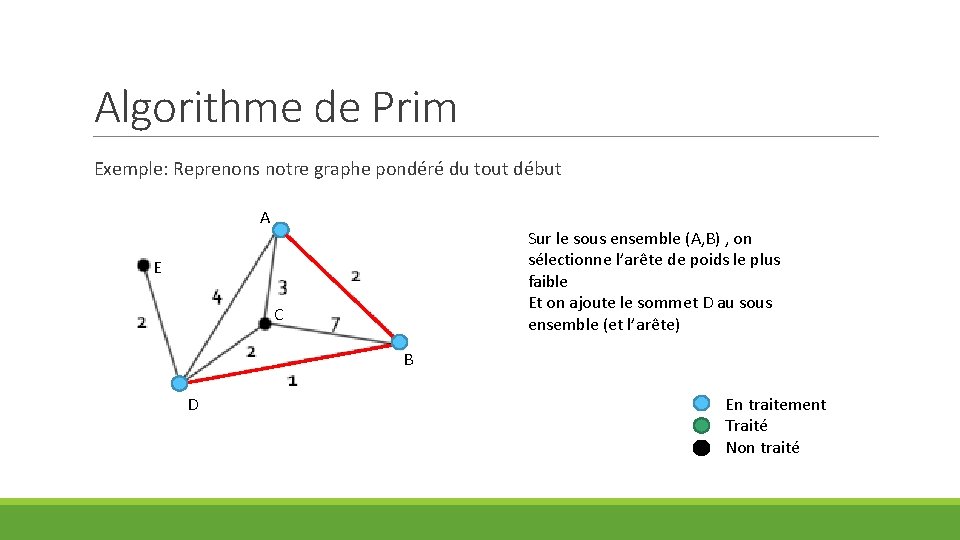
Algorithme de Prim Exemple: Reprenons notre graphe pondéré du tout début A Sur le sous ensemble (A, B) , on sélectionne l’arête de poids le plus faible Et on ajoute le sommet D au sous ensemble (et l’arête) E C B D En traitement Traité Non traité

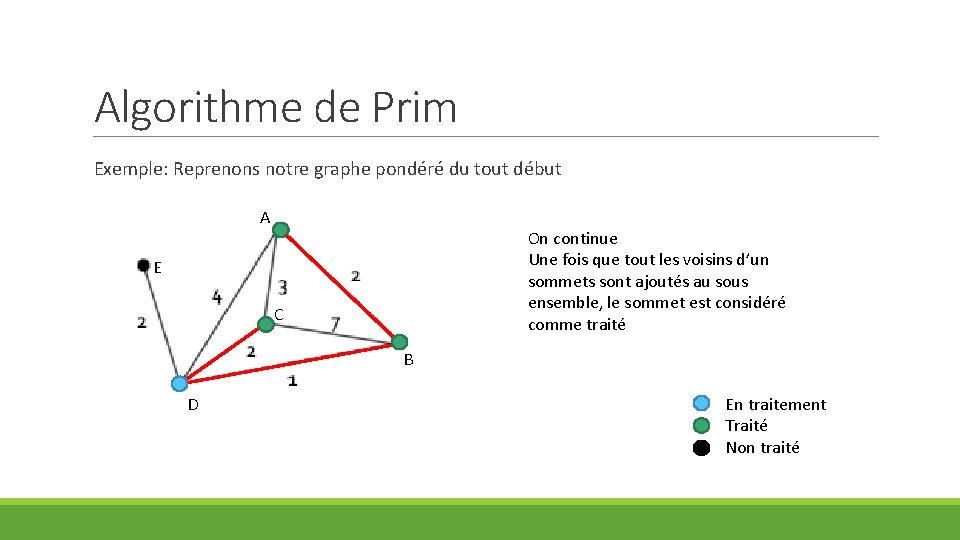
Algorithme de Prim Exemple: Reprenons notre graphe pondéré du tout début A On continue Une fois que tout les voisins d’un sommets sont ajoutés au sous ensemble, le sommet est considéré comme traité E C B D En traitement Traité Non traité

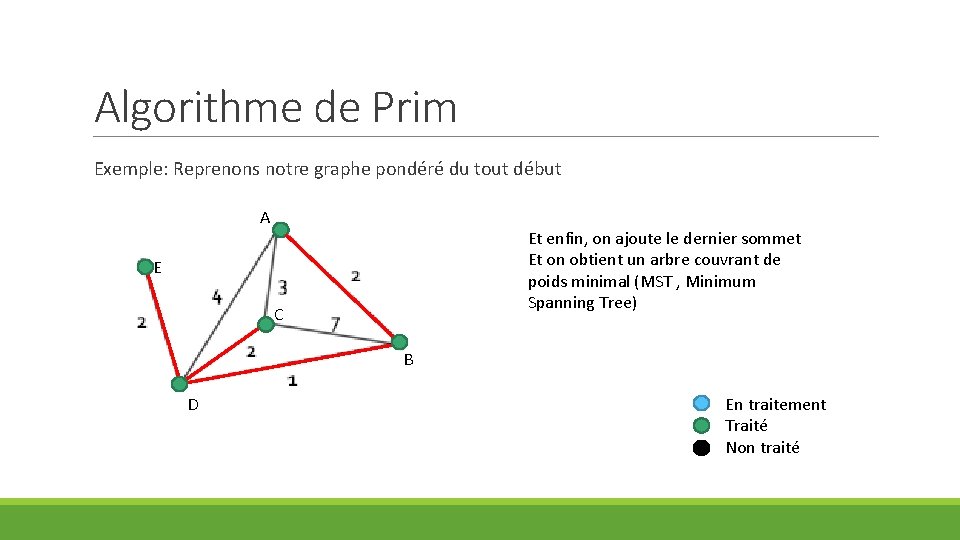
Algorithme de Prim Exemple: Reprenons notre graphe pondéré du tout début A Et enfin, on ajoute le dernier sommet Et on obtient un arbre couvrant de poids minimal (MST , Minimum Spanning Tree) E C B D En traitement Traité Non traité

Algorithme de Kruskal L’algorithme Kruskal est un autre algorithme de recherche d’arbre couvrant minimal mais il utilise une structure de donnée particulière non vue en cours le Union-Find. Principe: • Au début, l’arbre que l’ ne contient aucune arête, chaque sommet est isolé dans une composante connexe où il est seul • A chaque étape, on rajoute l’arête la moins chère qui permet de relier 2 composantes connexes disjointes • On s’arrête quand tous les sommets sont dans la même composante connexe

Algorithme de Kruskal « être dans la même composante connexe » est une relation d’équivalence Les fonctions créer. Ensemble, find et union sont celles de la structure de données Union-Find: • créer. Ensemble(v): ajoute la classe d’équivalence {v} • find(u): renvoie la classe d’équivalence de u • union(u, v): unit les classes d’équivalente de u et de v

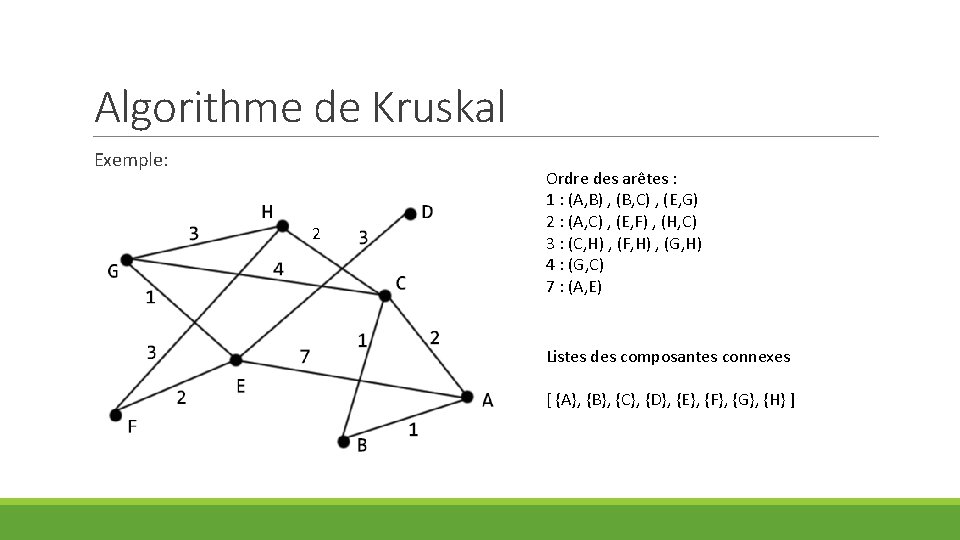
Algorithme de Kruskal Exemple: 2 Ordre des arêtes : 1 : (A, B) , (B, C) , (E, G) 2 : (A, C) , (E, F) , (H, C) 3 : (C, H) , (F, H) , (G, H) 4 : (G, C) 7 : (A, E) Listes des composantes connexes [ {A}, {B}, {C}, {D}, {E}, {F}, {G}, {H} ]

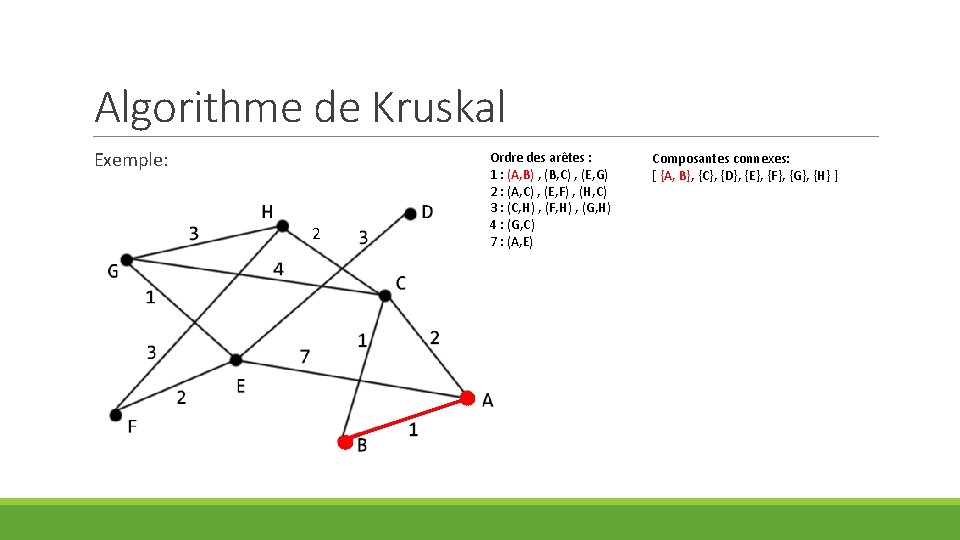
Algorithme de Kruskal Exemple: 2 Ordre des arêtes : 1 : (A, B) , (B, C) , (E, G) 2 : (A, C) , (E, F) , (H, C) 3 : (C, H) , (F, H) , (G, H) 4 : (G, C) 7 : (A, E) Composantes connexes: [ {A, B}, {C}, {D}, {E}, {F}, {G}, {H} ]

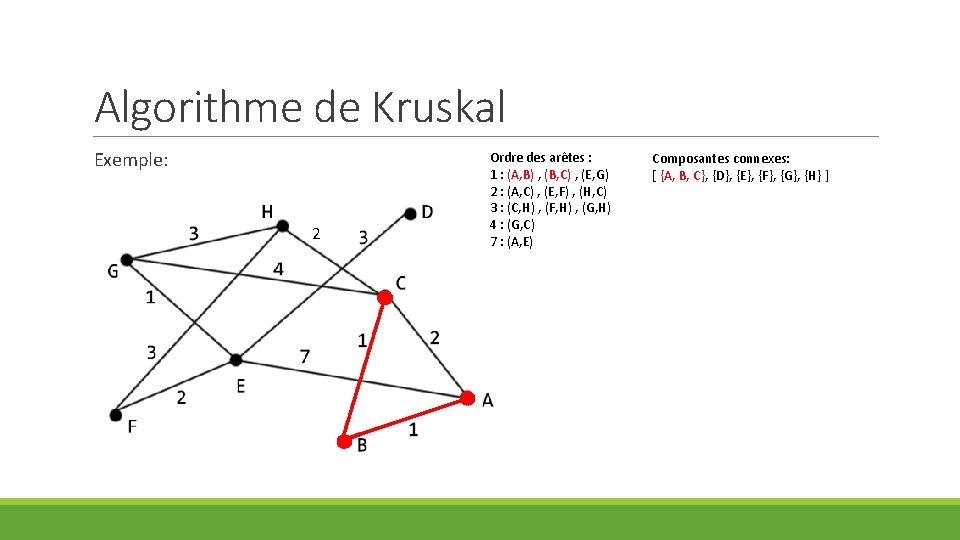
Algorithme de Kruskal Exemple: 2 Ordre des arêtes : 1 : (A, B) , (B, C) , (E, G) 2 : (A, C) , (E, F) , (H, C) 3 : (C, H) , (F, H) , (G, H) 4 : (G, C) 7 : (A, E) Composantes connexes: [ {A, B, C}, {D}, {E}, {F}, {G}, {H} ]

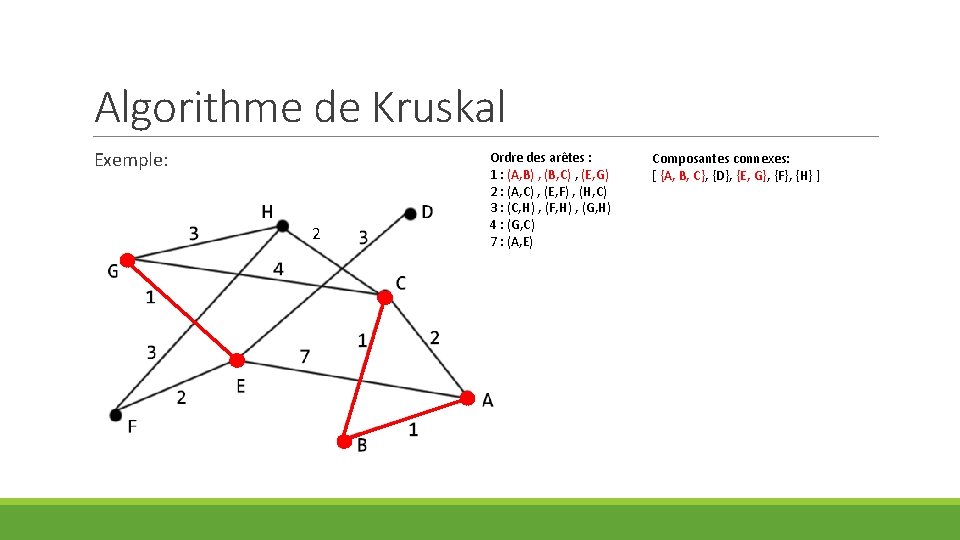
Algorithme de Kruskal Exemple: 2 Ordre des arêtes : 1 : (A, B) , (B, C) , (E, G) 2 : (A, C) , (E, F) , (H, C) 3 : (C, H) , (F, H) , (G, H) 4 : (G, C) 7 : (A, E) Composantes connexes: [ {A, B, C}, {D}, {E, G}, {F}, {H} ]

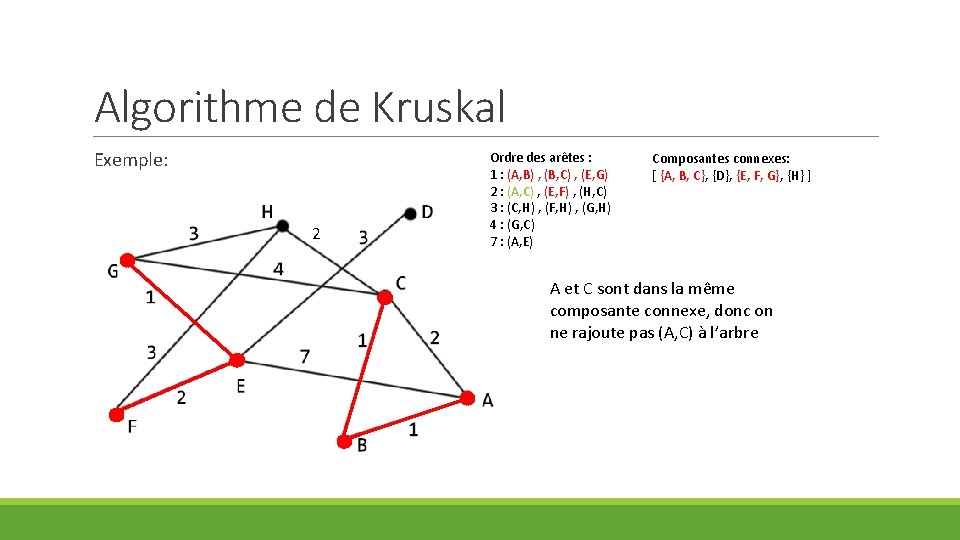
Algorithme de Kruskal Exemple: 2 Ordre des arêtes : 1 : (A, B) , (B, C) , (E, G) 2 : (A, C) , (E, F) , (H, C) 3 : (C, H) , (F, H) , (G, H) 4 : (G, C) 7 : (A, E) Composantes connexes: [ {A, B, C}, {D}, {E, F, G}, {H} ] A et C sont dans la même composante connexe, donc on ne rajoute pas (A, C) à l’arbre

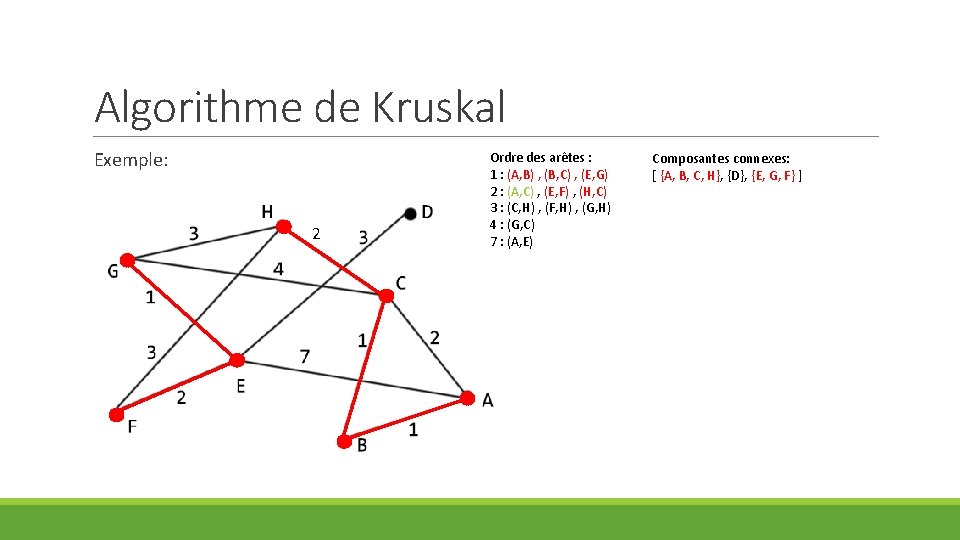
Algorithme de Kruskal Exemple: 2 Ordre des arêtes : 1 : (A, B) , (B, C) , (E, G) 2 : (A, C) , (E, F) , (H, C) 3 : (C, H) , (F, H) , (G, H) 4 : (G, C) 7 : (A, E) Composantes connexes: [ {A, B, C, H}, {D}, {E, G, F} ]

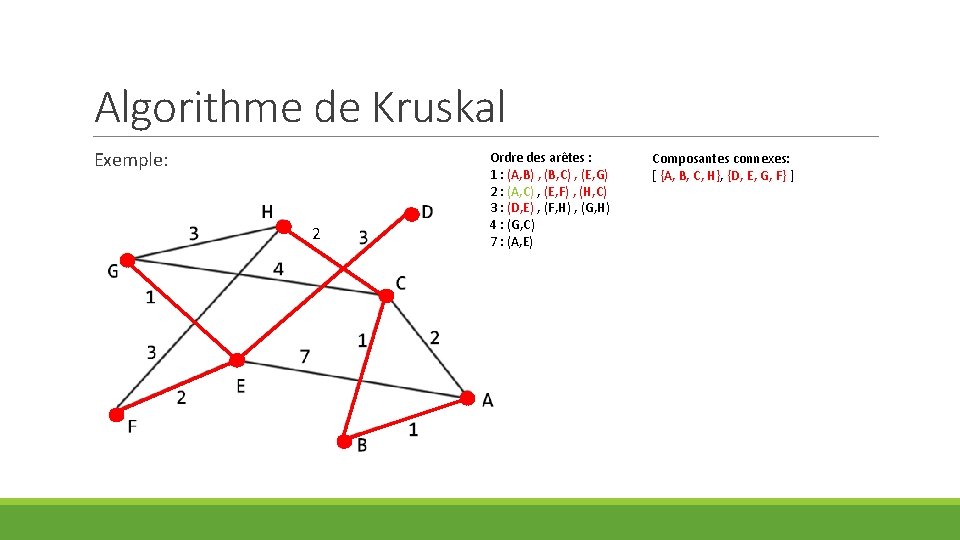
Algorithme de Kruskal Exemple: 2 Ordre des arêtes : 1 : (A, B) , (B, C) , (E, G) 2 : (A, C) , (E, F) , (H, C) 3 : (D, E) , (F, H) , (G, H) 4 : (G, C) 7 : (A, E) Composantes connexes: [ {A, B, C, H}, {D, E, G, F} ]

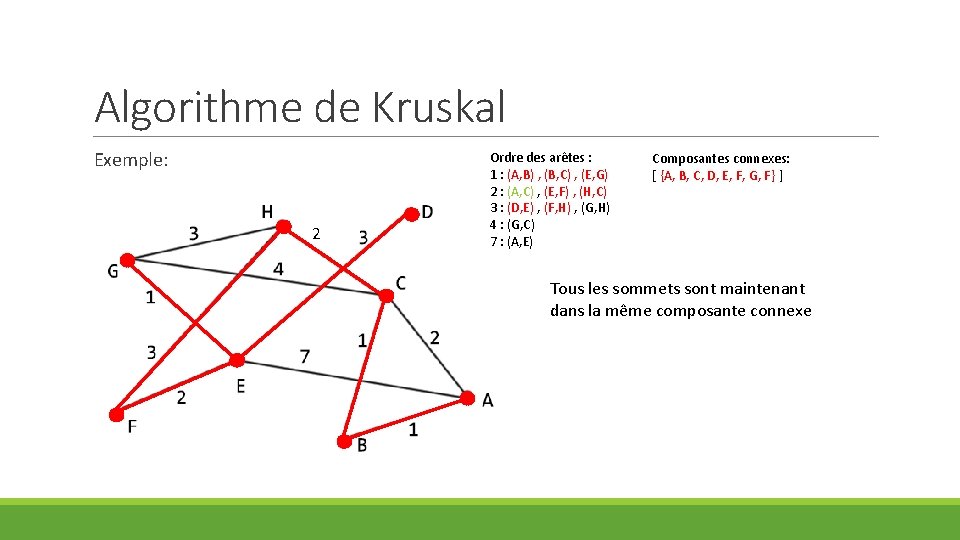
Algorithme de Kruskal Exemple: 2 Ordre des arêtes : 1 : (A, B) , (B, C) , (E, G) 2 : (A, C) , (E, F) , (H, C) 3 : (D, E) , (F, H) , (G, H) 4 : (G, C) 7 : (A, E) Composantes connexes: [ {A, B, C, D, E, F, G, F} ] Tous les sommets sont maintenant dans la même composante connexe

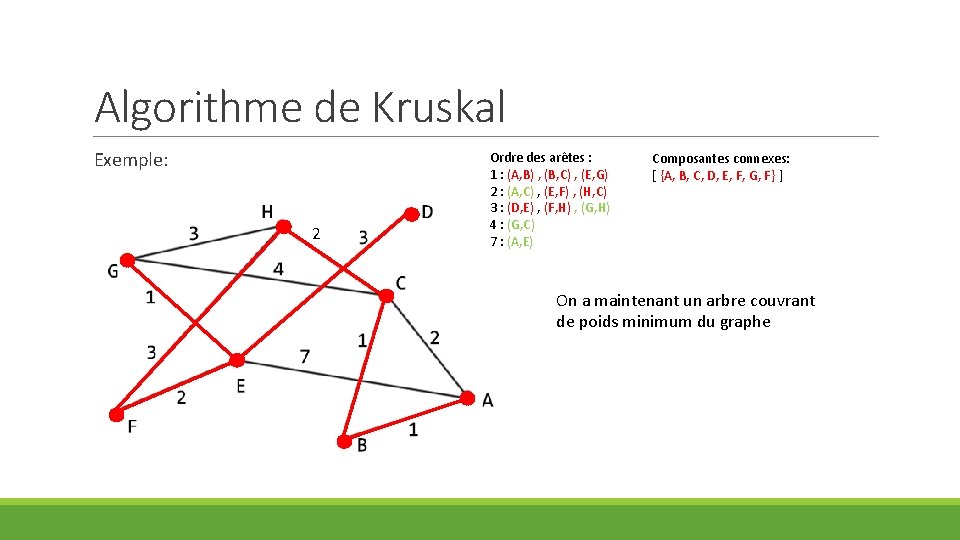
Algorithme de Kruskal Exemple: 2 Ordre des arêtes : 1 : (A, B) , (B, C) , (E, G) 2 : (A, C) , (E, F) , (H, C) 3 : (D, E) , (F, H) , (G, H) 4 : (G, C) 7 : (A, E) Composantes connexes: [ {A, B, C, D, E, F, G, F} ] On a maintenant un arbre couvrant de poids minimum du graphe

Algorithme de Kruskal « être dans la même composante connexe » est une relation d’équivalence Les fonctions créer. Ensemble, find et union sont celles de la structure de données Union-Find: • créer. Ensemble(v): ajoute la classe d’équivalence {v} • find(u): renvoie la classe d’équivalence de u • union(u, v): unit les classes d’équivalente de u et de v

Coloration de graphe

Coloration de graphe : définitions Comment colorer un graphe de telle sorte que deux nœuds adjacents soient de couleurs différentes ? Couleur : nombre entier, généralement entre 0 et n-1 χ(G) : nombre minimal de couleurs pour colorer G

Coloration de graphe : pourquoi ? Exemple de problème: création d’équipes: §Modélisation par un graphe § Nœuds: personnes § Arêtes: (u, v) est une arête du graphe si u et v ne veulent pas être ensemble §Peut-on créer 2 équipes en respectant les rivalités ? §Réponse: oui, si le graphe est biparti

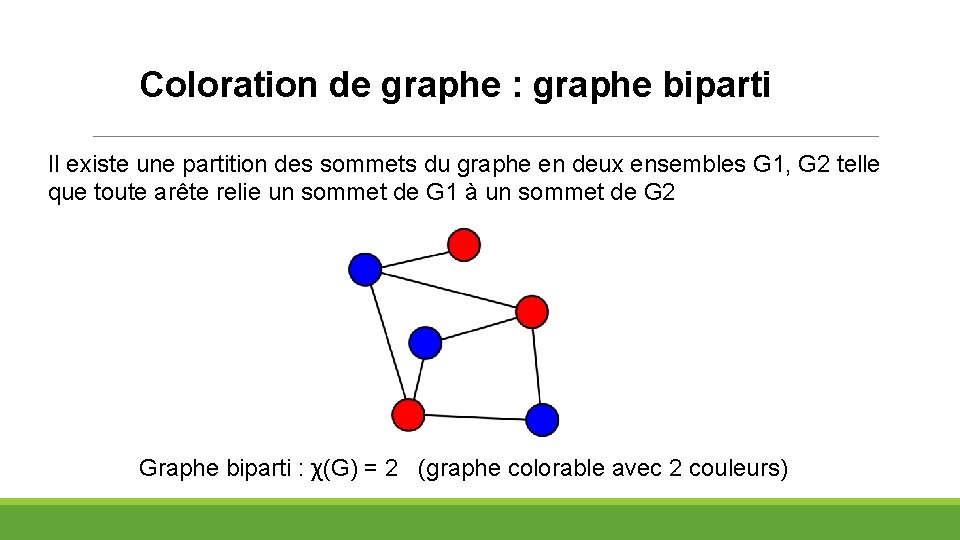
Coloration de graphe : graphe biparti Il existe une partition des sommets du graphe en deux ensembles G 1, G 2 telle que toute arête relie un sommet de G 1 à un sommet de G 2 Graphe biparti : χ(G) = 2 (graphe colorable avec 2 couleurs)

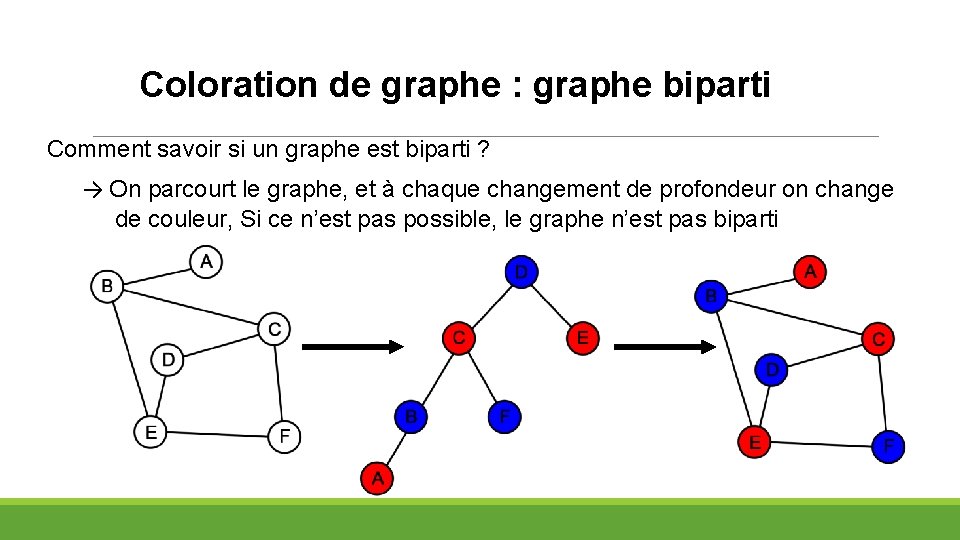
Coloration de graphe : graphe biparti Comment savoir si un graphe est biparti ? → On parcourt le graphe, et à chaque changement de profondeur on change de couleur, Si ce n’est pas possible, le graphe n’est pas biparti

Coloration de graphe : comment faire ? Quel algorithme permet de colorer un graphe ? Quid de l’optimalité ? Deux algorithmes principaux : - Algorithme glouton, naïf, non optimal mais rapide - Backtracking, complexité élevée mais permet d’avoir un résultat optimal

Coloration de graphe : algorithme glouton Algorithme glouton : avance étape par étape, choisit une solution optimale localement, sans souci d’optimalité globale. Principe : on parcourt le graphe (en profondeur, largeur ou autre), et à chaque nœud on assigne la première couleur possible (en fonctions des voisins déjà colorés). Problème : le nombre de couleurs dépend du nœud de départ, de la manière de parcourir le graphe…

Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées :

Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées :

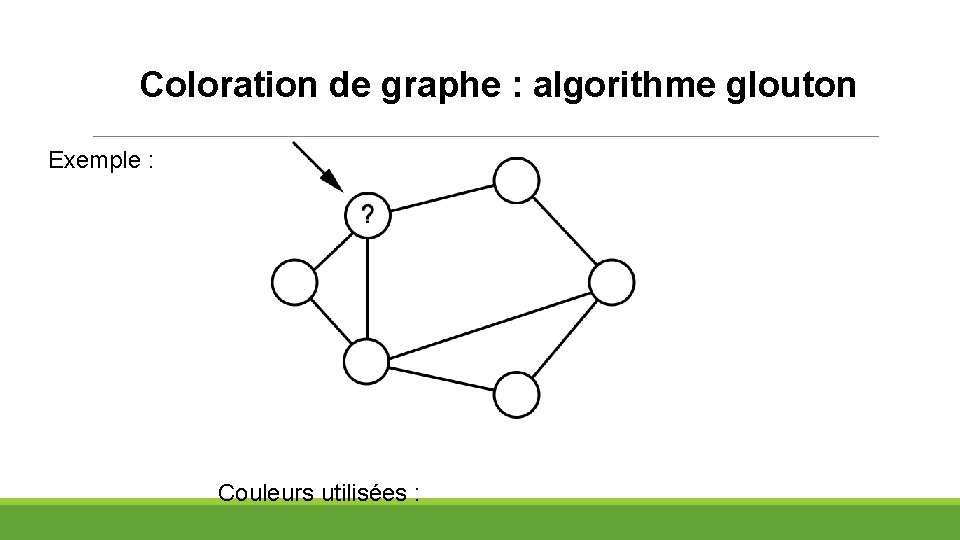
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées :

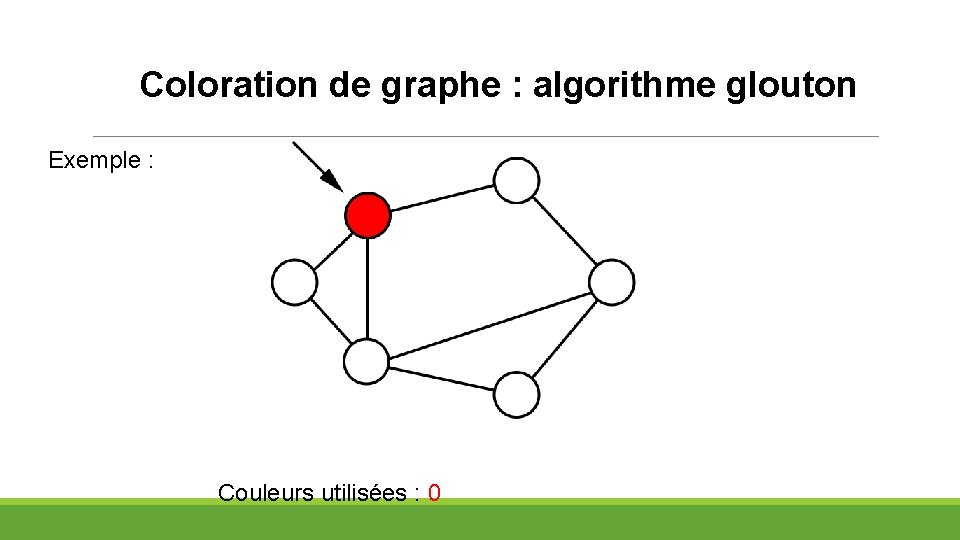
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0

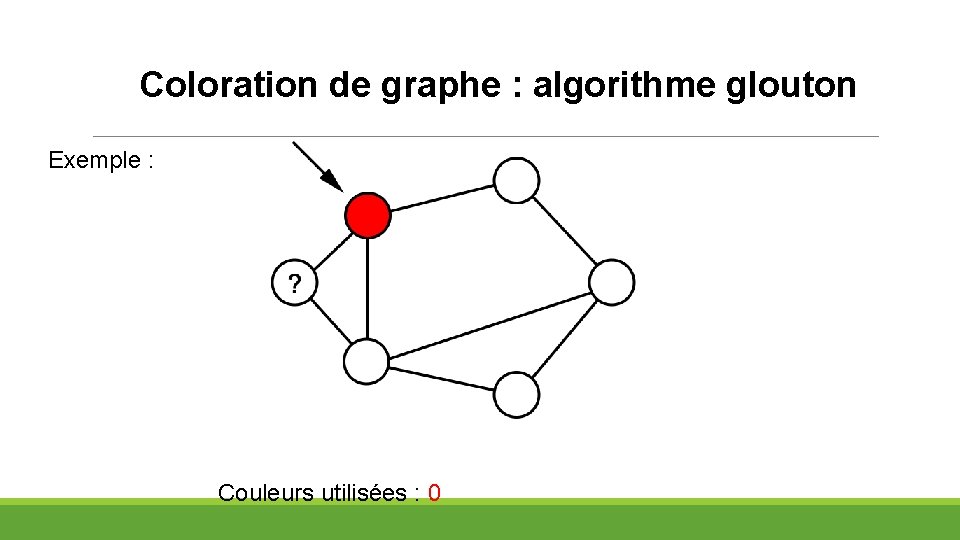
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0

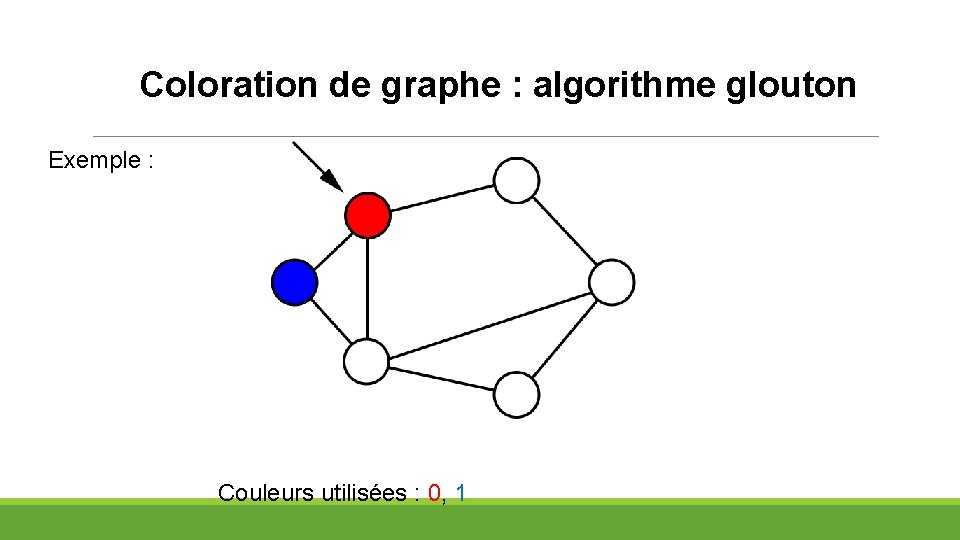
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1

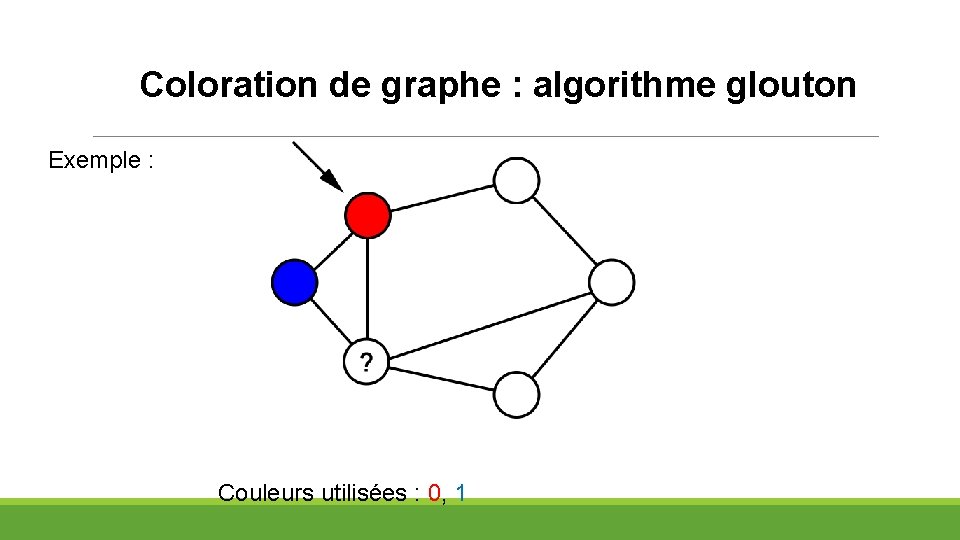
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1

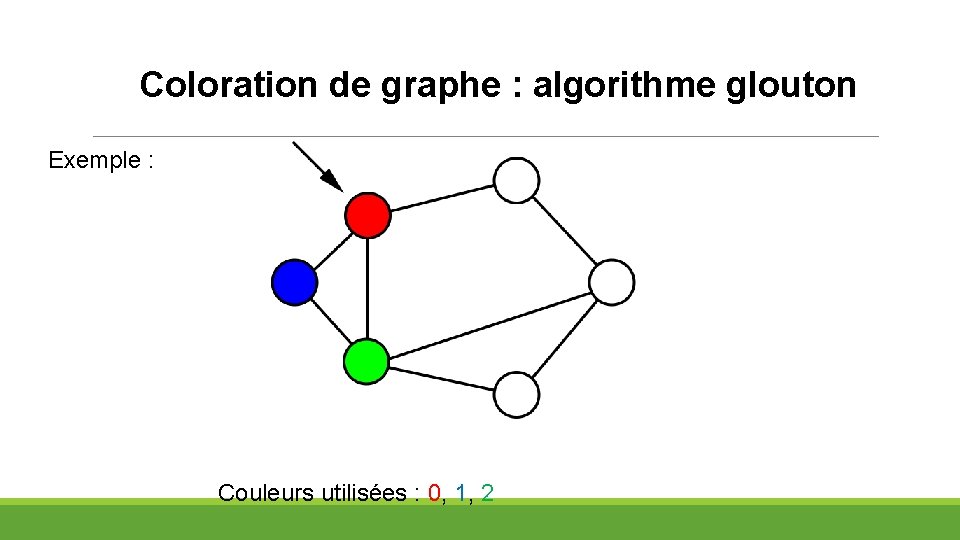
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

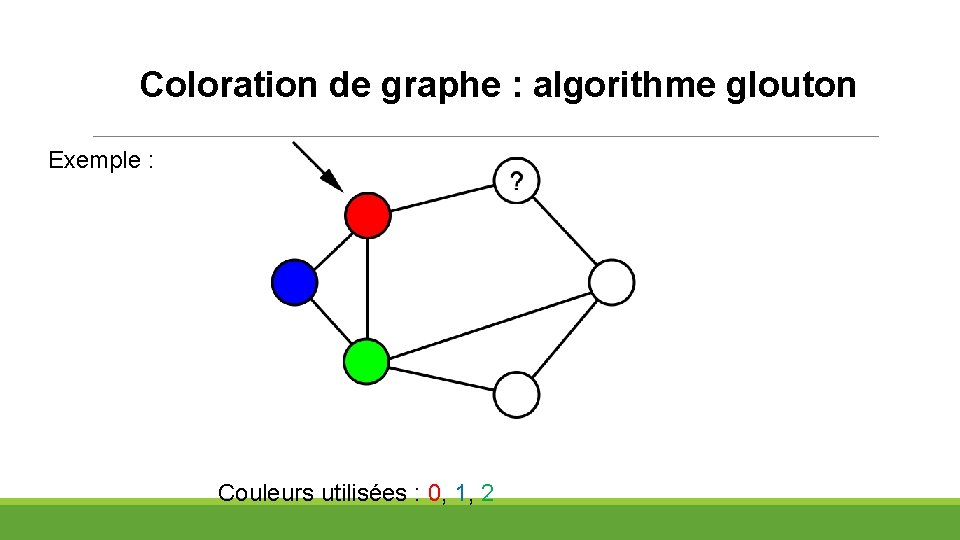
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

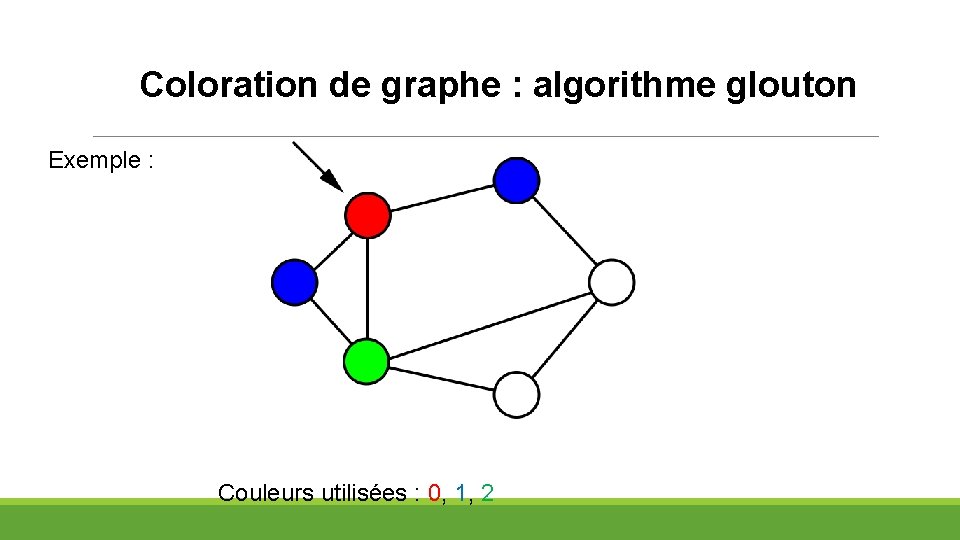
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

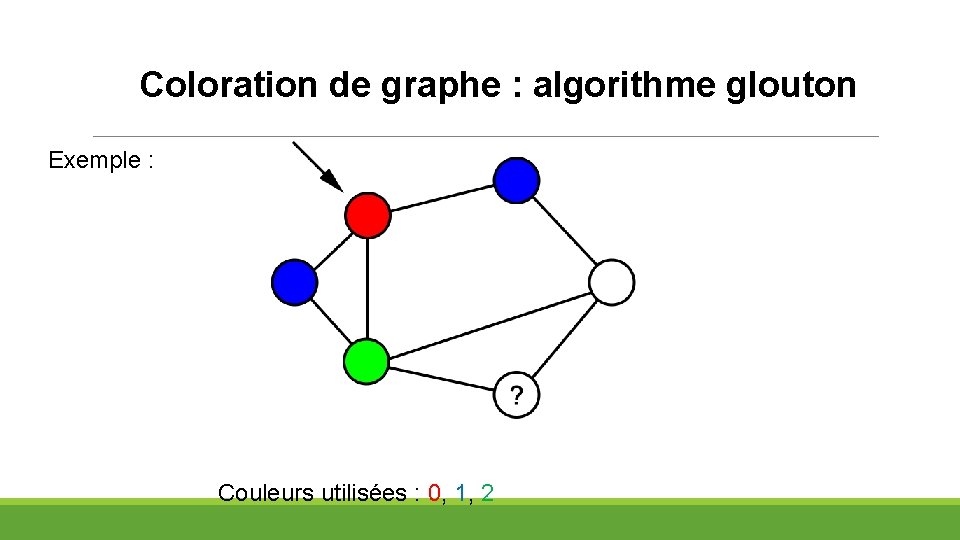
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

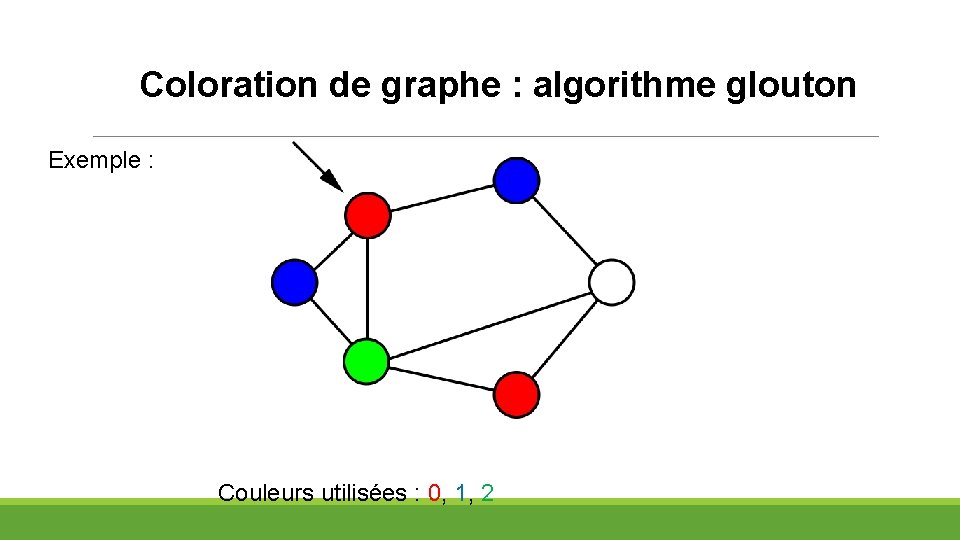
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

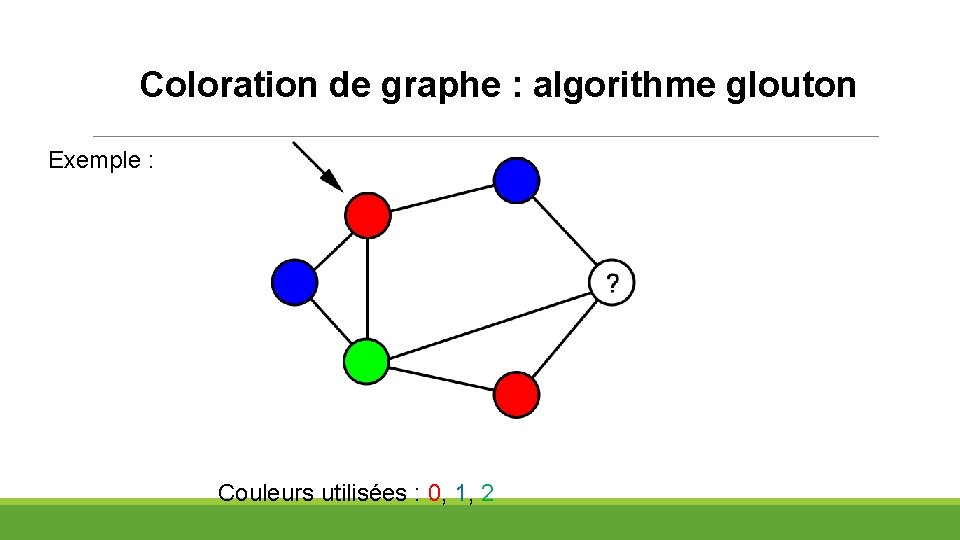
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

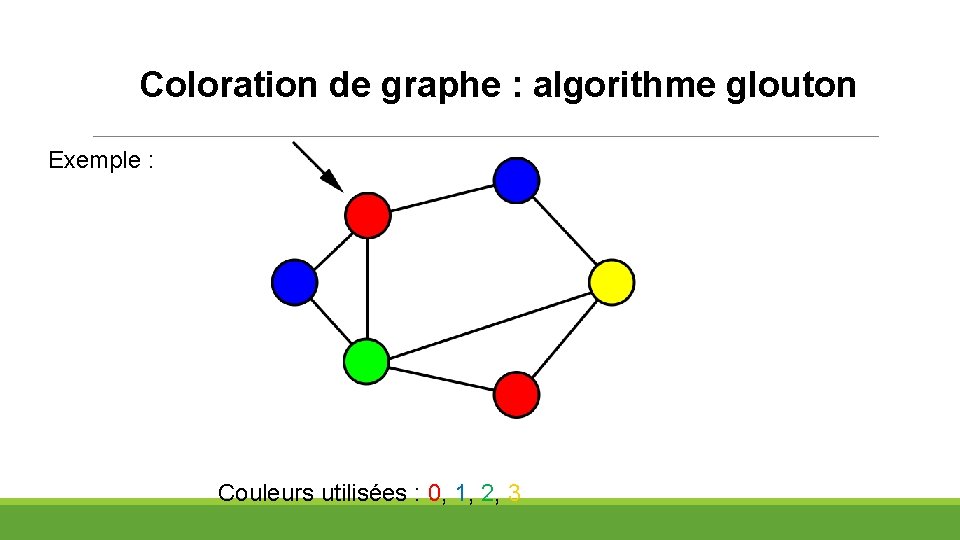
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2, 3

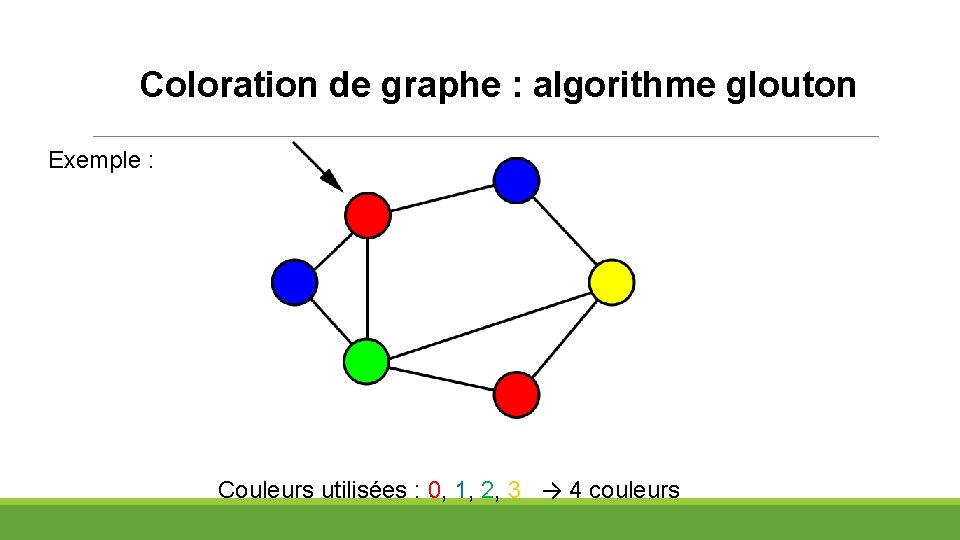
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2, 3 → 4 couleurs

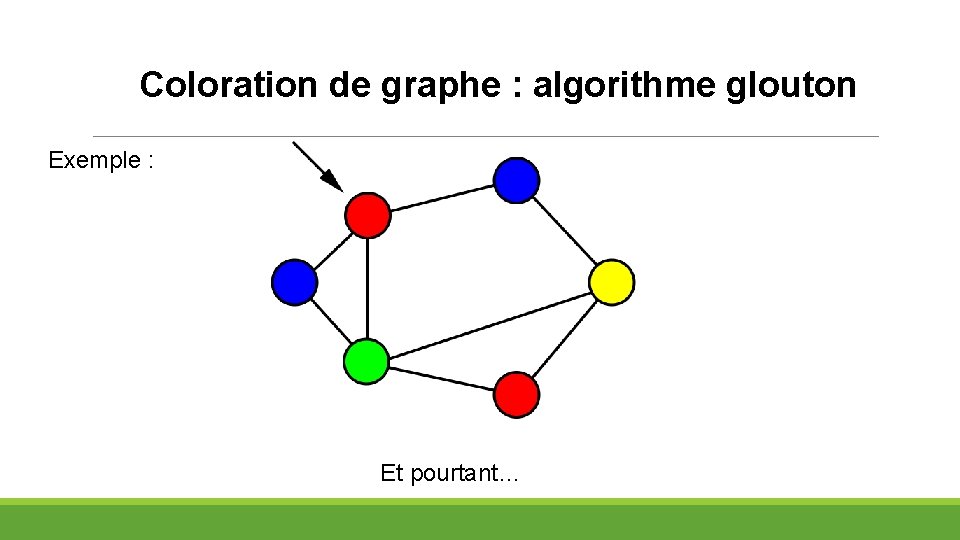
Coloration de graphe : algorithme glouton Exemple : Et pourtant…

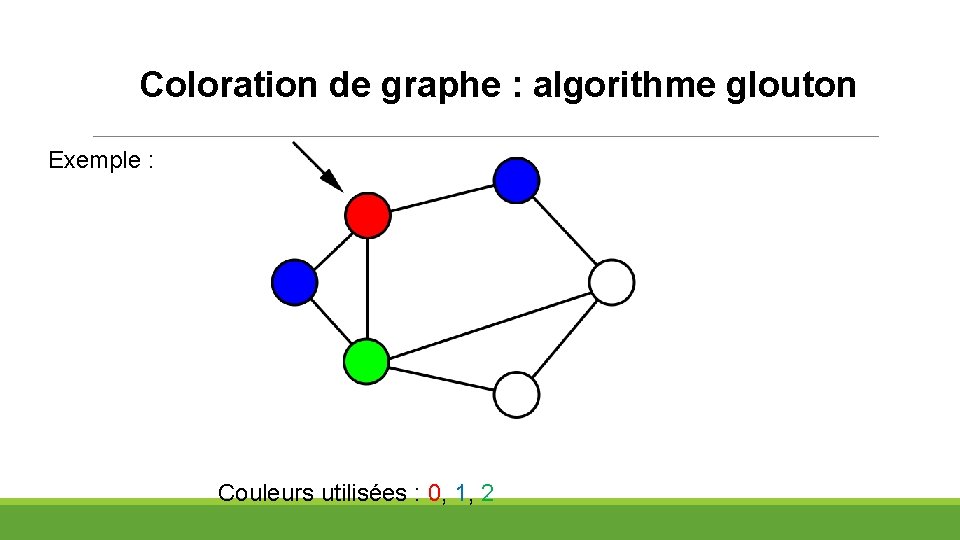
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

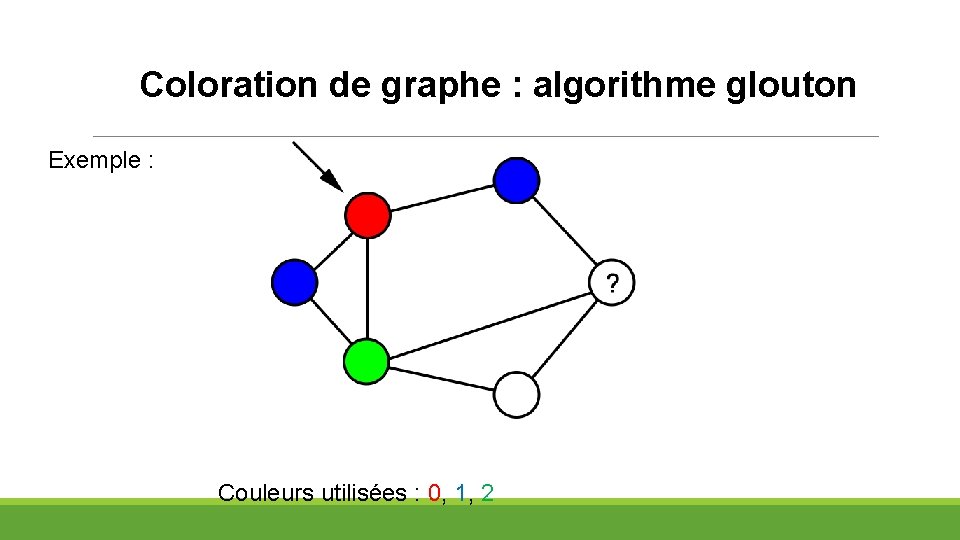
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

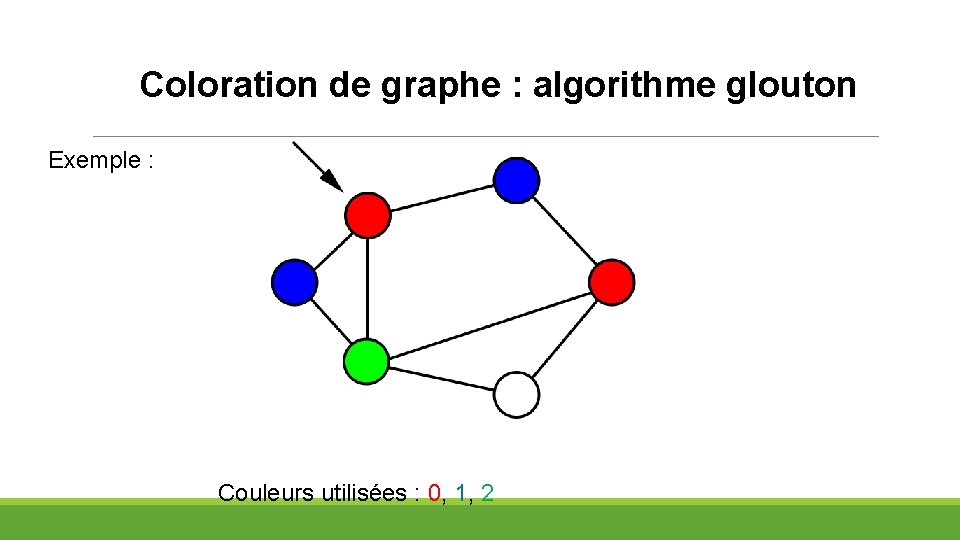
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

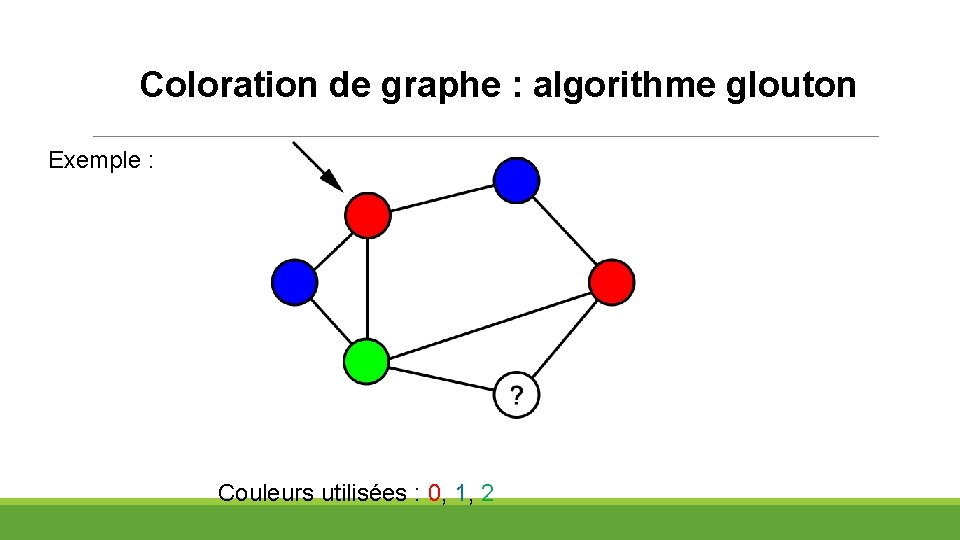
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

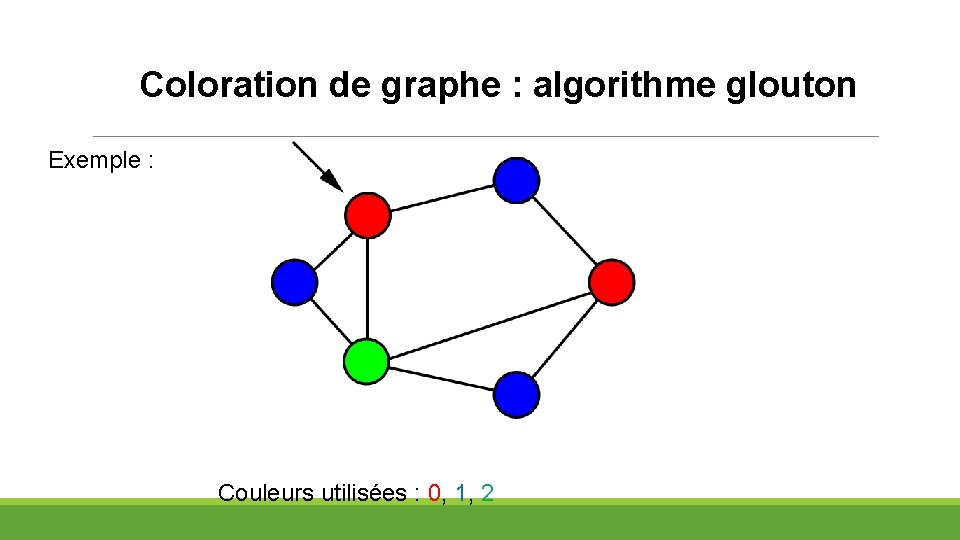
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2

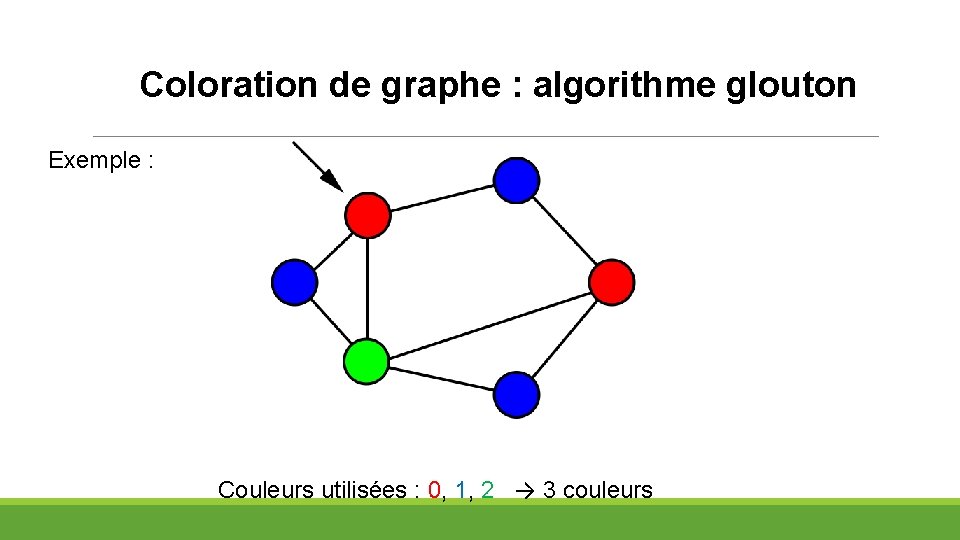
Coloration de graphe : algorithme glouton Exemple : Couleurs utilisées : 0, 1, 2 → 3 couleurs

Coloration de graphe : algorithme glouton

Coloration de graphe : algorithme glouton Le nombre de couleurs utilisé ≤ Δ(G) +1 (Δ(G) = degré de G = nombre maximal d’arêtes partant d’un nœud) Complexité : Θ(|V|+|E|)

Le backtracking (et son application à la coloration de graphe)

Le backtracking : schéma général Principe général : revenir légèrement en arrière sur les décisions prises en cas de blocage Utilisé surtout dans la programmation sous contraintes : - Colorer un graphe - Problème des n dames - Résolution d’une grille de sudoku - Mise en place d’emplois du temps - …

Le backtracking : schéma général On veut créer un algorithme qui renvoie True si une solution à notre problème (avec ses contraintes) existe, et False sinon (variante : stocker une ou toutes les solutions trouvées et les renvoyer). « revenir légèrement en arrière » : par récursivité, on ne crée pas de fonction que revient explicitement sur une étape précédente !

Le backtracking : schéma général Schéma de l’algorithme :

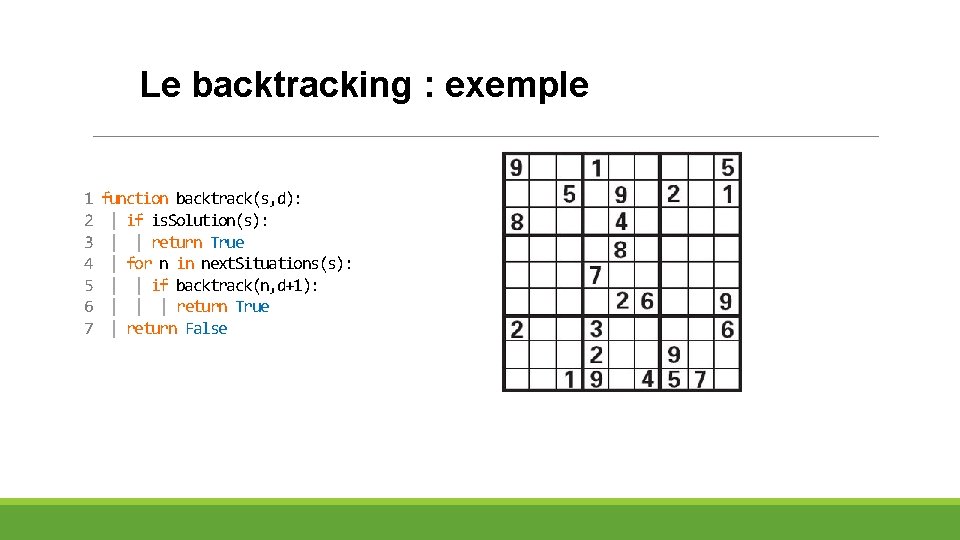
Le backtracking : exemple 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

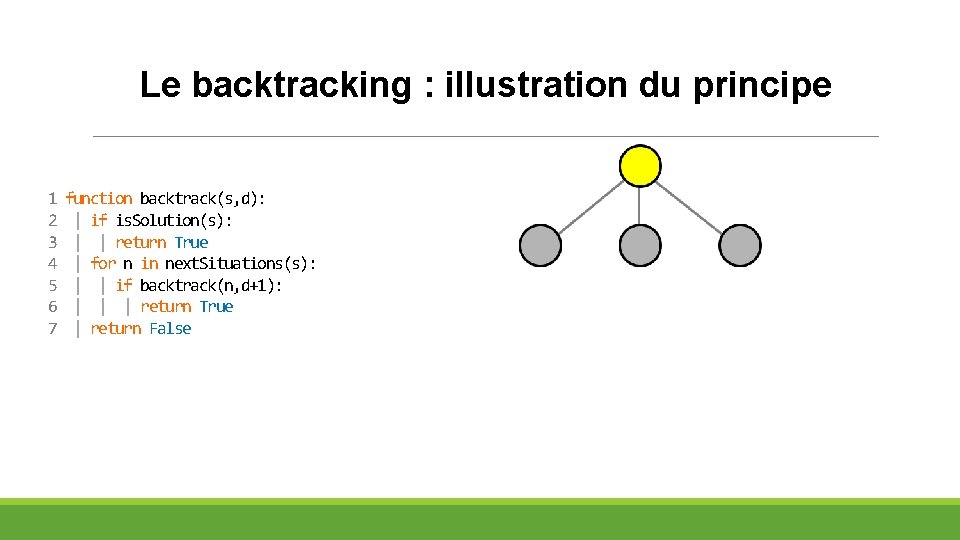
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

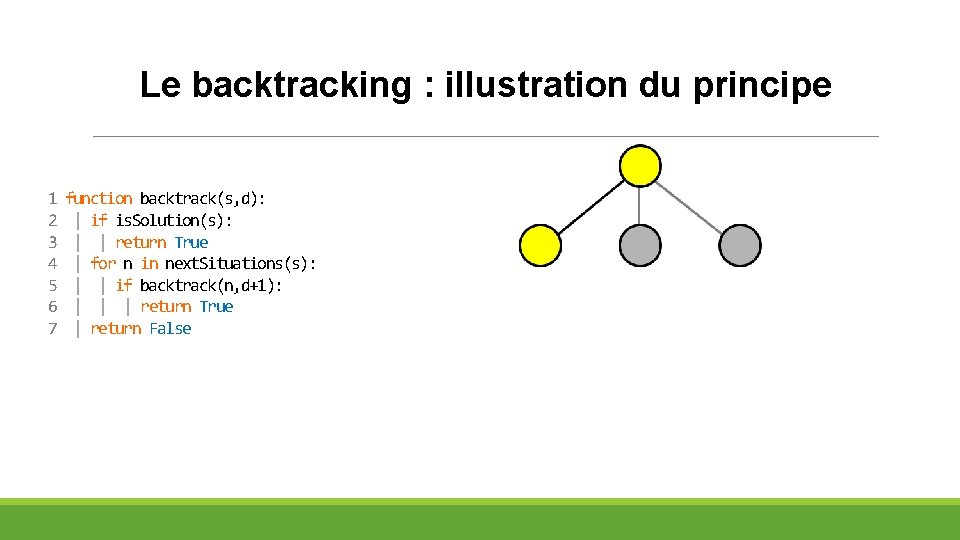
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

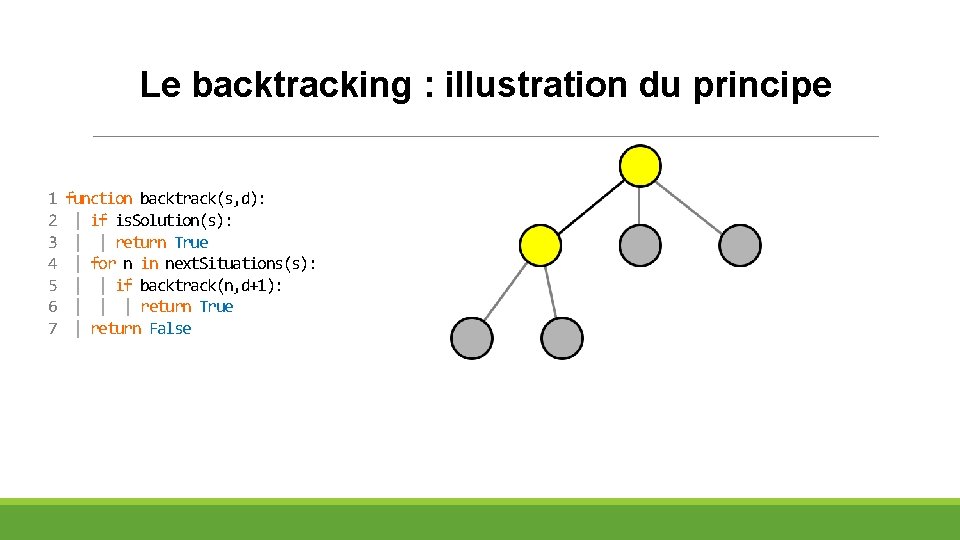
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

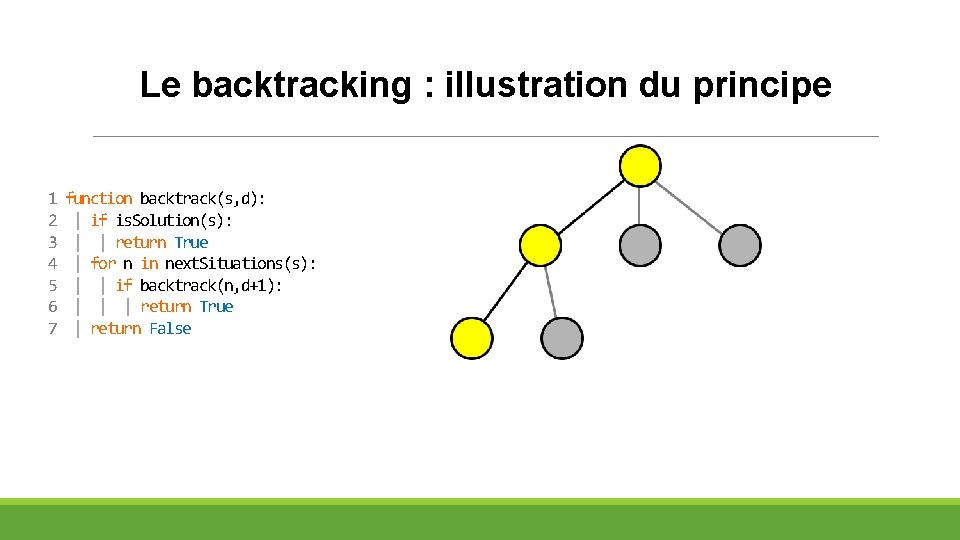
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

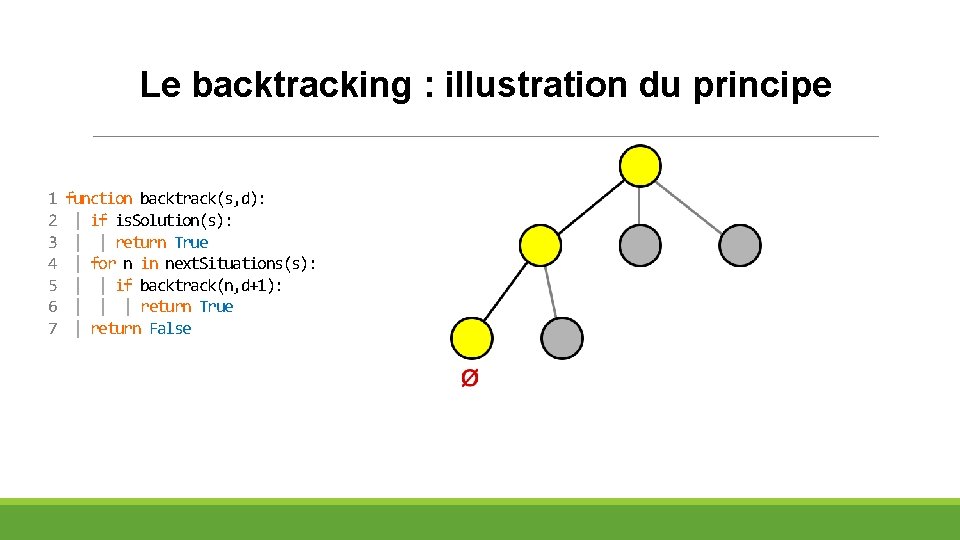
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

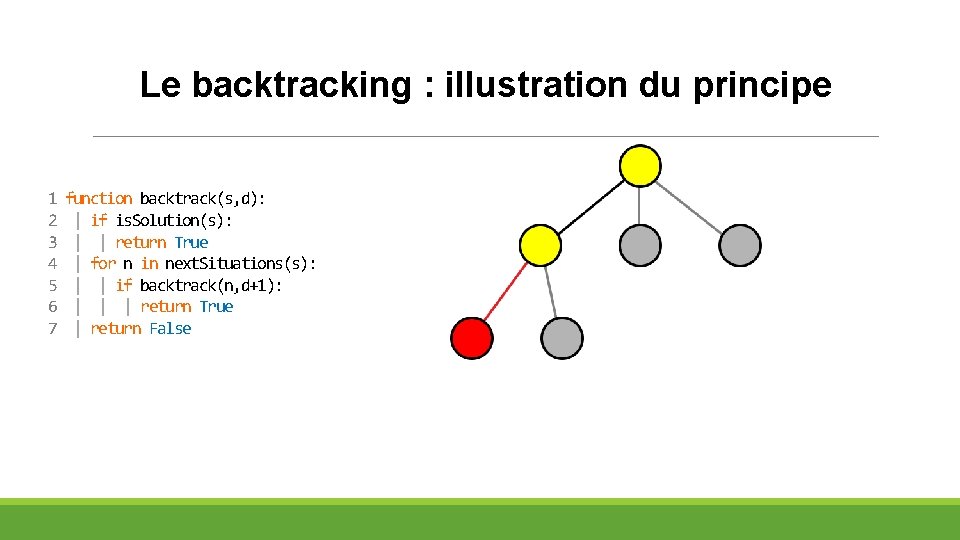
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

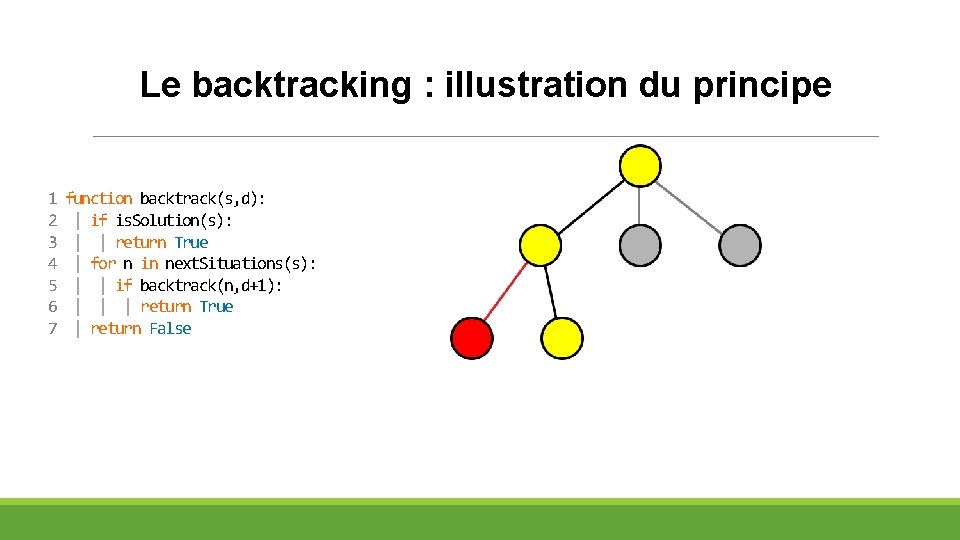
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

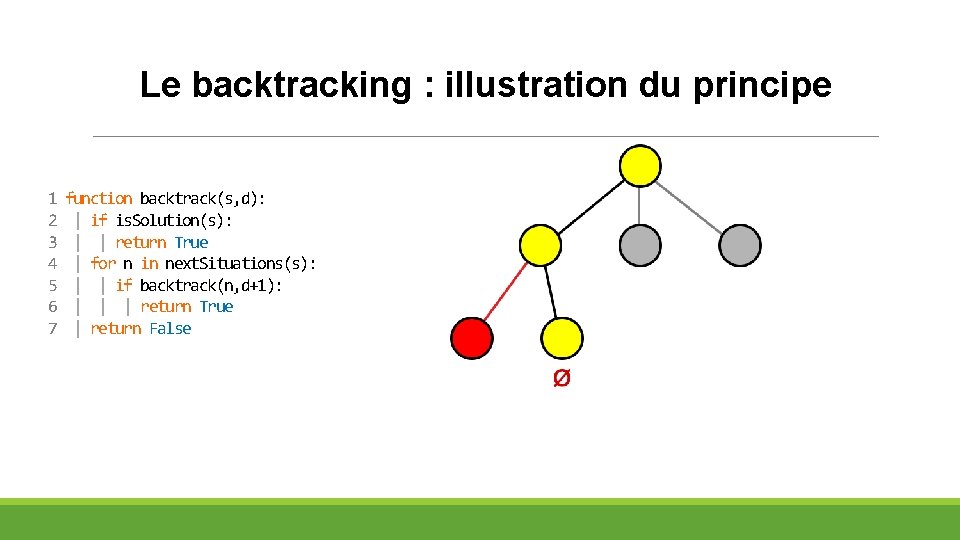
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

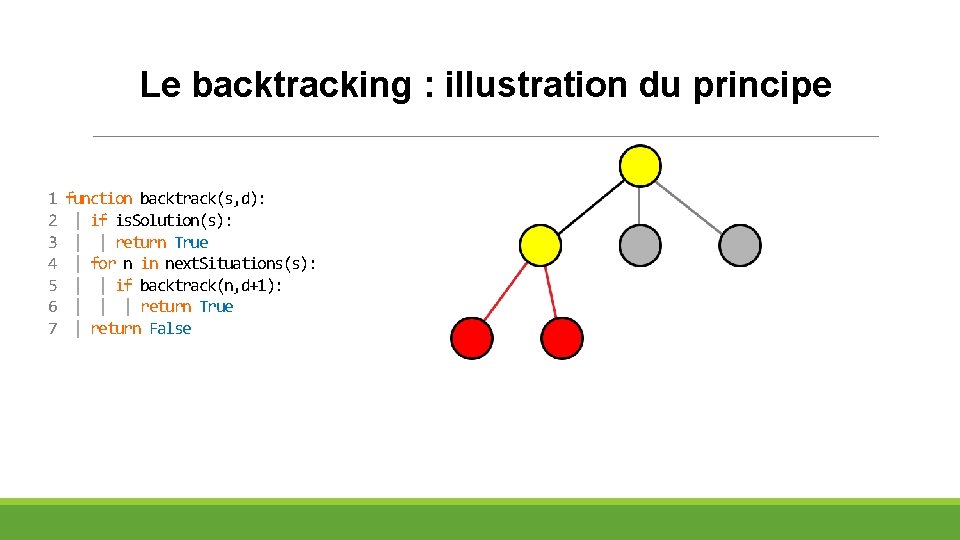
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

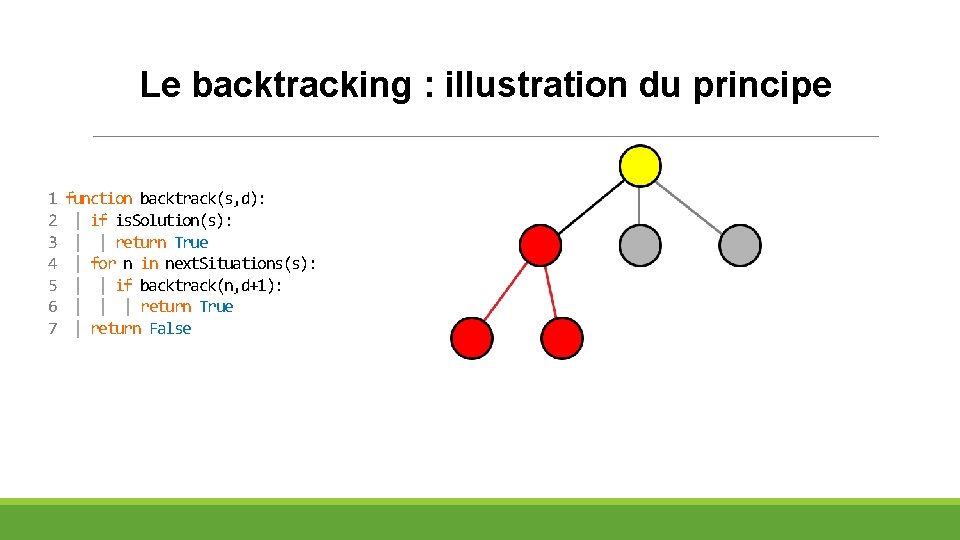
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

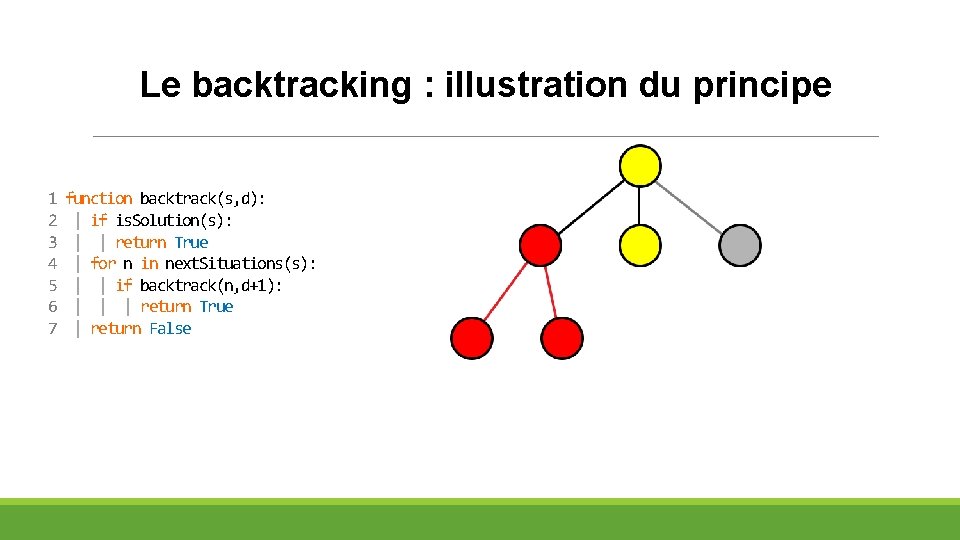
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

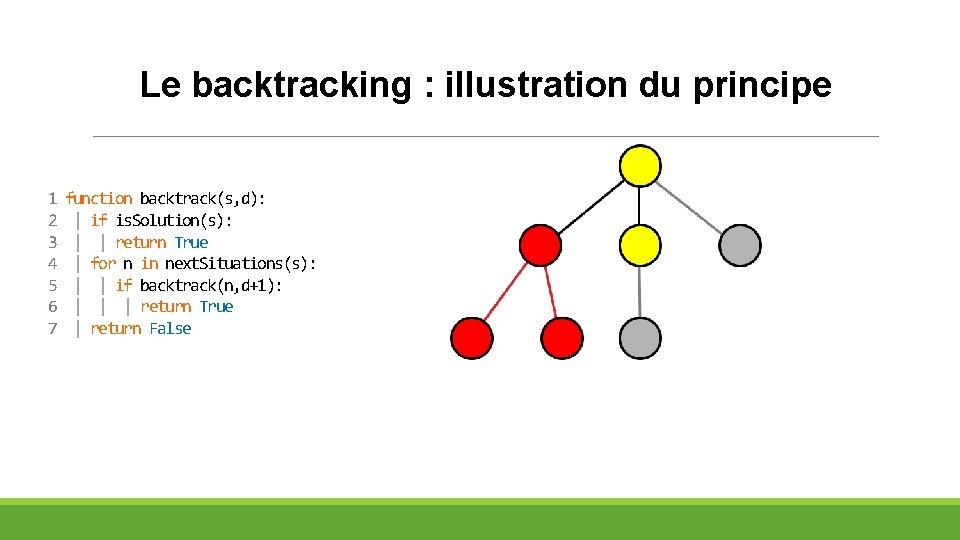
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

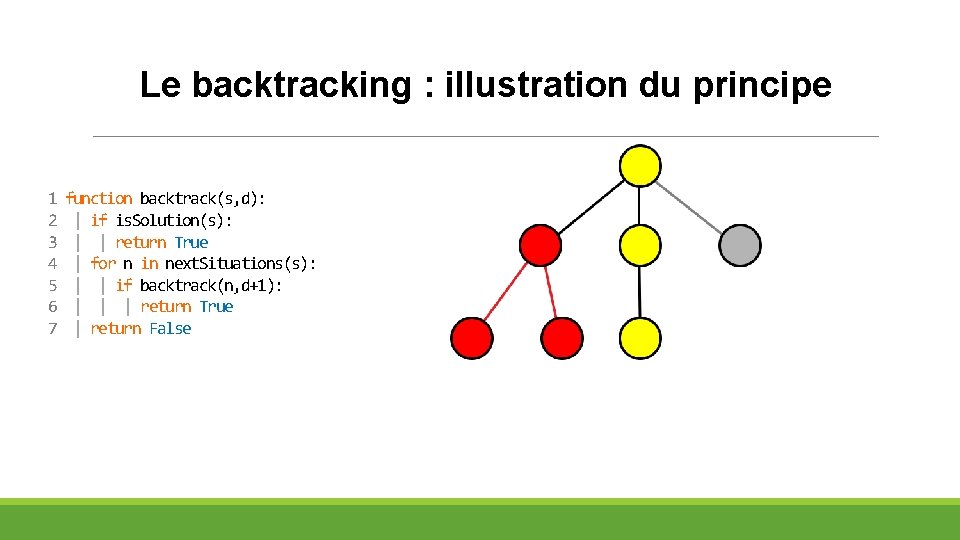
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

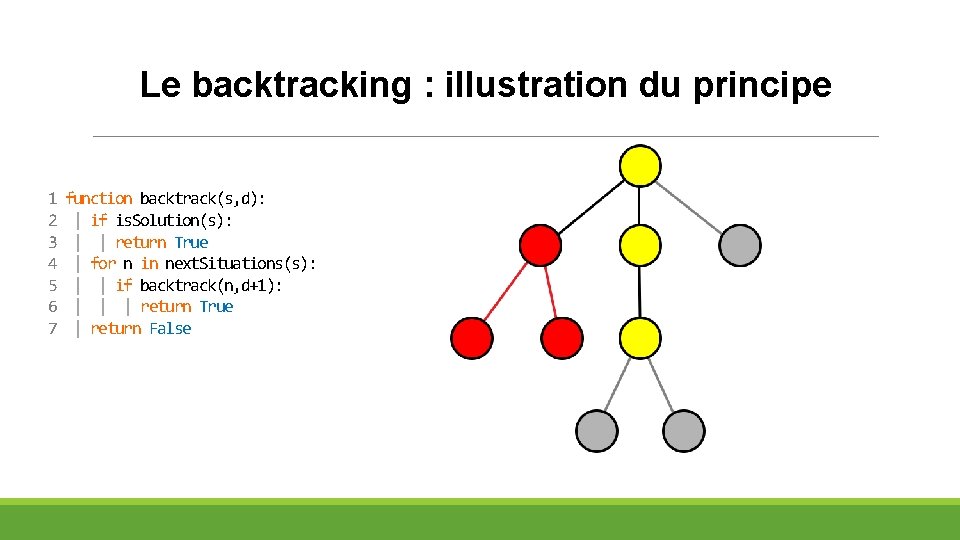
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

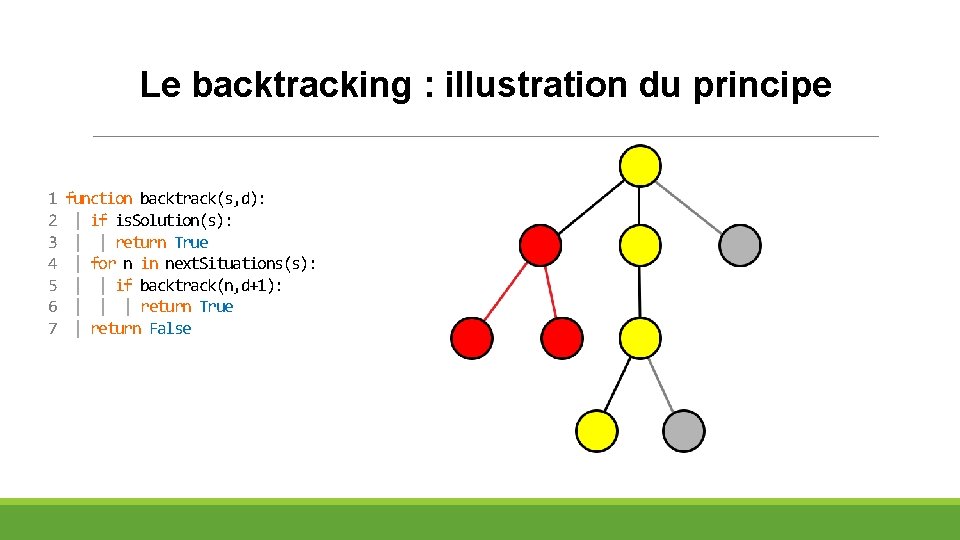
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

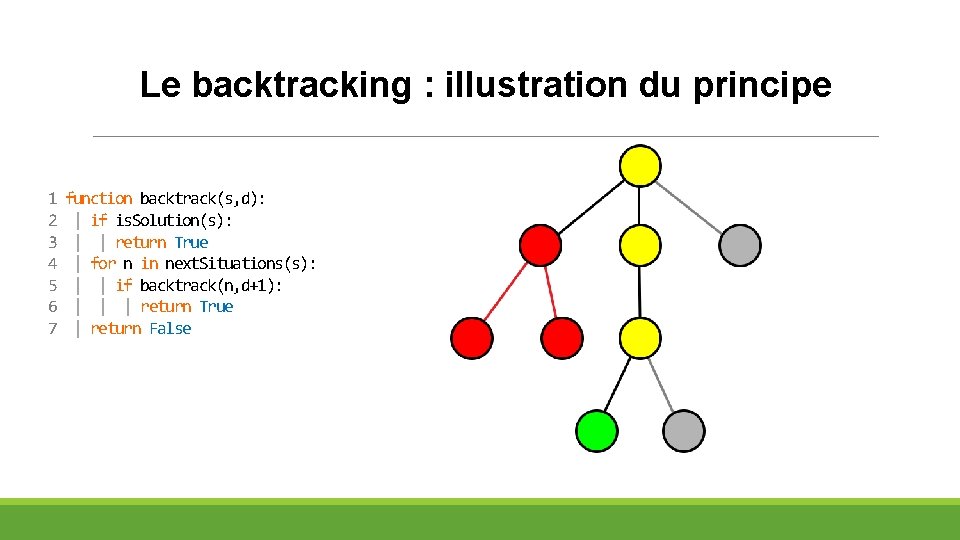
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

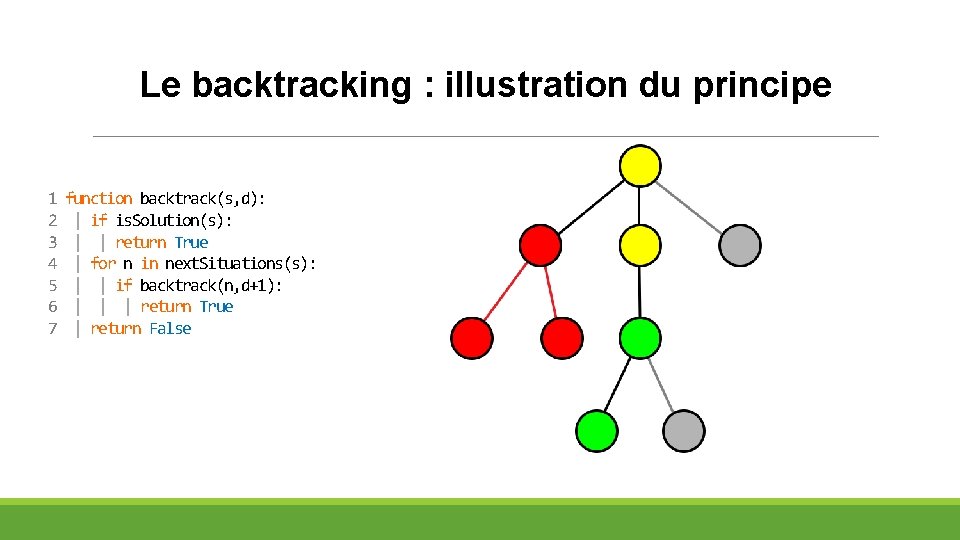
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

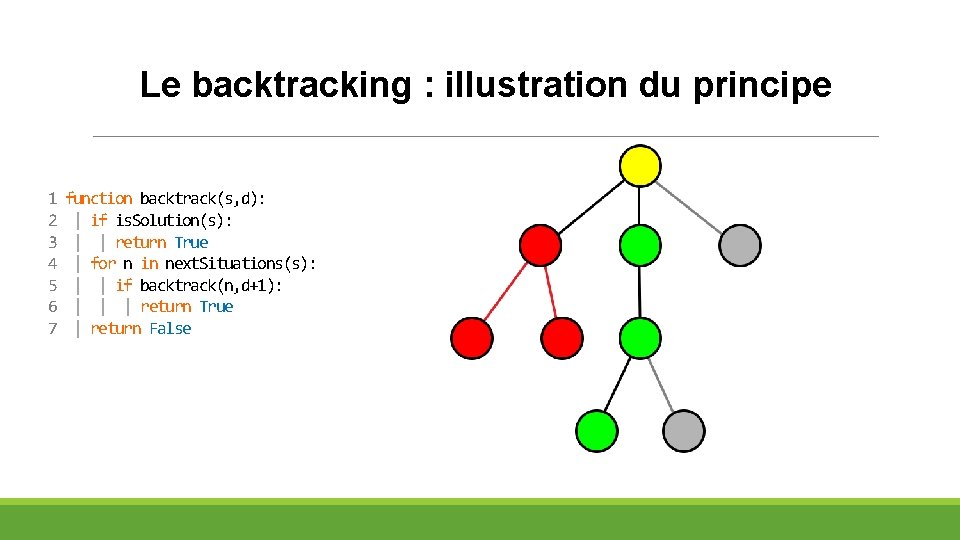
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

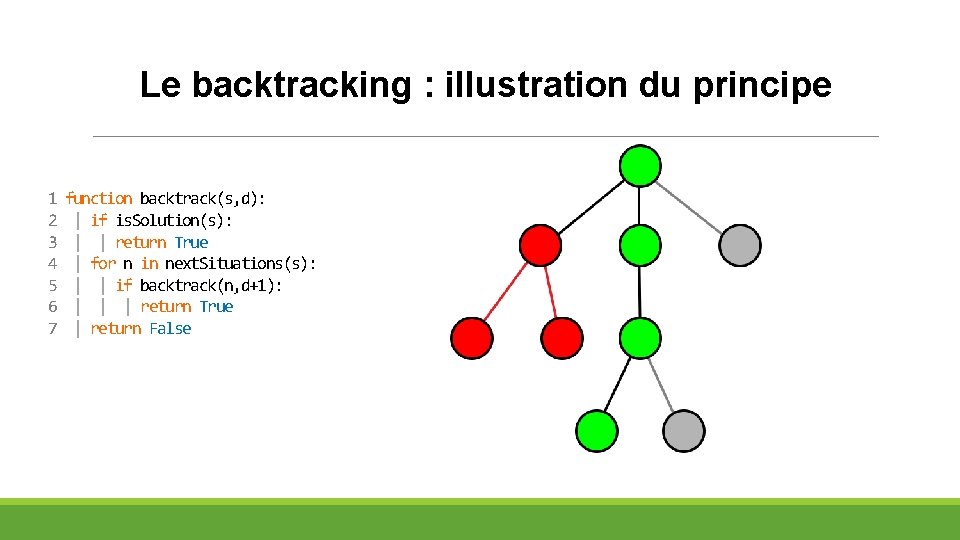
Le backtracking : illustration du principe 1 2 3 4 5 6 7 function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False

Le backtracking : attention Attention: - Soigner la situation d’arrêt (valable pour tout algorithme récursif) - Si le problème peut présenter un cycle (on peut revenir à un état déjà traité), il faut trouver un moyen de repérer les états déjà parcourus (attribut, stockage dans un dictionnaire, …) - La complexité du backtracking est exponentielle, en Θ(bd) avec `b` le facteur de branchement et `d` la profondeur maximale de récursion, car si la solution qui marche est dans la dernière branche parcourue, on a du étudier tous les cas avant de la trouver

Le backtracking : coloration de graphe max. Color = n function backtrack(s, d): | if is. Solution(s): | | return True | for n in next. Situations(s): | | if backtrack(n, d+1): | | | return True | return False function backtrack. Color(G, k): # k : noeud courant | if k = |V(G)|: | | return True | for c ← 0 to max. Color: | | V(G)[k]. color ← c | | if not c in [n. color for n in neighbors(V(G)[k])]: | | | if backtrack. Color(G, k+1): | | return True | V(G)[k]. color ← -1 # décolorer le sommet | return False L’algorithme renvoie True si le graphe est colorable avec max. Color couleurs.

Le backtracking : coloration de graphe optimale En adaptant cet algorithme, il est possible d’obtenir χ(G) en adaptant le code (attention, ce n’est plus vraiment du backtracking) max. Color = n max. Color ← ∞ function backtrack. Color(G, k): | if k = |V(G)|: | | return True | for c ← 0 to max. Color: | | V(G)[k]. color ← c | | if not c in [n. color for n in neighbors(V(G)[k])]: | | | if backtrack. Color(G, k+1): | | return True | V(G)[k]. color ← -1 | return False Attention, function backtrack. Color. Opt(G, k): | if k = |V(G)|: | | max. Color ← min(max. Color, count. Colors(G)) | for c ← 0 to max. Color: | | V(G)[k]. color ← c | | if not c in [n. color for n in neighbors(V(G)[k])]: | | | backtrack. Color. Opt(G, k+1): | V(G)[k]. color ← -1 la complexité est énorme, on calcule toutes les colorations possibles du graphe ! Il faudrait arrêter d’explorer une branche dès qu’on sait qu’elle ne donnera pas une meilleur coloration -> branch and bound.

Branch and bound (séparation et évaluation)

Branch and bound : principe • Branch : séparer l’ensemble des solutions en ensembles plus petits • Bound : évaluer ces sous-ensembles et n’explorer que ceux pouvant contenir une solution meilleure que la meilleure solution courante (par majoration). « solution courante » : on stocke la meilleure solution trouvée jusqu’à présent par l’algorithme. Comme du backtracking, sauf que: • Une fois qu’on a trouvé une solution, on continue de cher une meilleure solution • On ne va pas jusqu’au bout des branches qui ne donneront pas une meilleure solution

Branch and bound : comment s’y prendre ? Comment savoir si un ensemble de solutions ne contient pas de solution optimale ? → Déterminer une borne inférieure pour le coût des solutions de cet ensemble (s'il s'agit d'un problème de minimisation). Si cette borne inférieure est de coût supérieur au coût de la meilleure solution courante, le sous-ensemble ne contient pas d'optimum.

Branch and bound : complexité En théorie la même que celle du backtracking : exponentielle, en Θ(bd) (dans le pire cas, on explore toutes les branches…) En pratique, on peut arriver bien plus vite à une solution optimale (ou acceptable, on peut s’arrêter quand on veut) Utilisations : - Problèmes d’optimisation - IA (échecs, …)

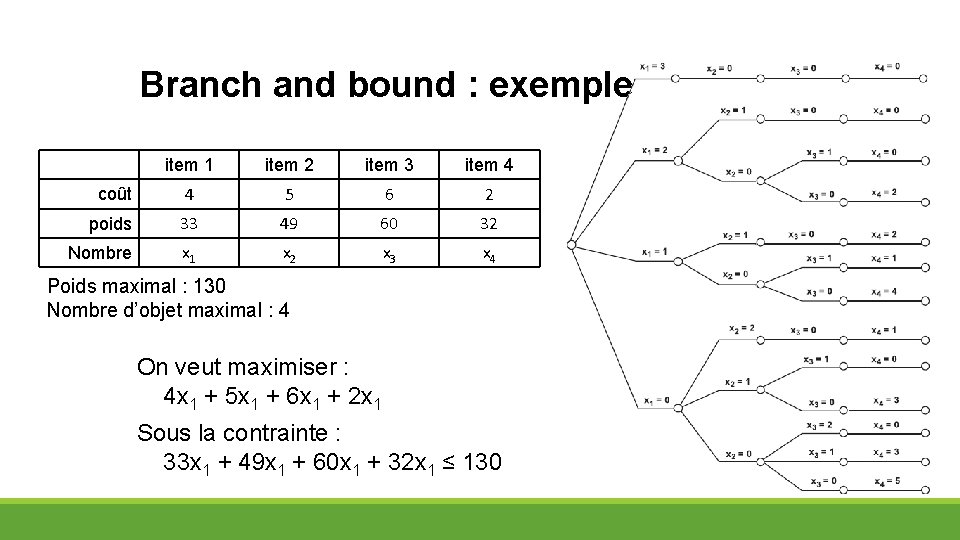
Branch and bound : exemple item 1 item 2 item 3 item 4 coût 4 5 6 2 poids 33 49 60 32 Nombre x 1 x 2 x 3 x 4 Poids maximal : 130 Nombre d’objet maximal : 4 On veut maximiser : 4 x 1 + 5 x 1 + 6 x 1 + 2 x 1 Sous la contrainte : 33 x 1 + 49 x 1 + 60 x 1 + 32 x 1 ≤ 130

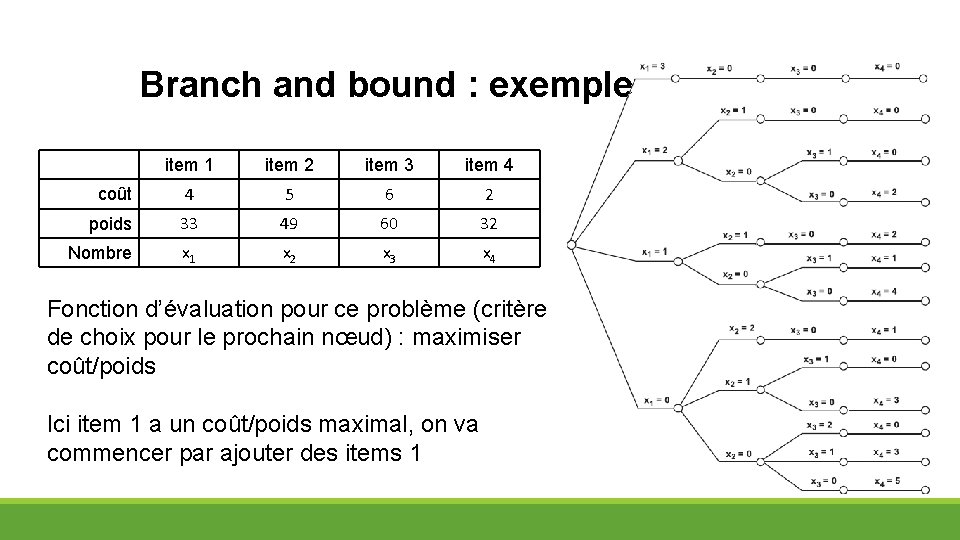
Branch and bound : exemple item 1 item 2 item 3 item 4 coût 4 5 6 2 poids 33 49 60 32 Nombre x 1 x 2 x 3 x 4 Fonction d’évaluation pour ce problème (critère de choix pour le prochain nœud) : maximiser coût/poids Ici item 1 a un coût/poids maximal, on va commencer par ajouter des items 1

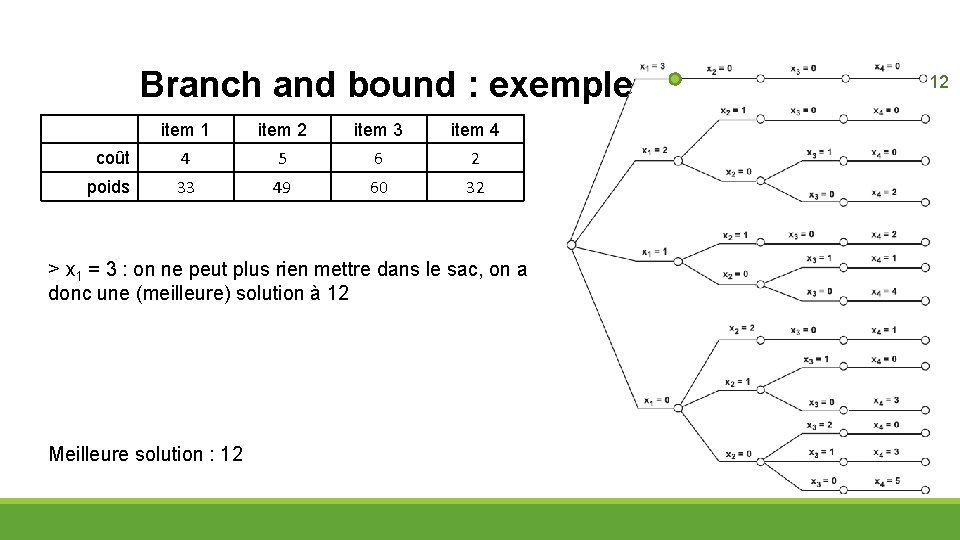
Branch and bound : exemple item 1 item 2 item 3 item 4 coût 4 5 6 2 poids 33 49 60 32 > x 1 = 3 : on ne peut plus rien mettre dans le sac, on a donc une (meilleure) solution à 12 Meilleure solution : 12 12

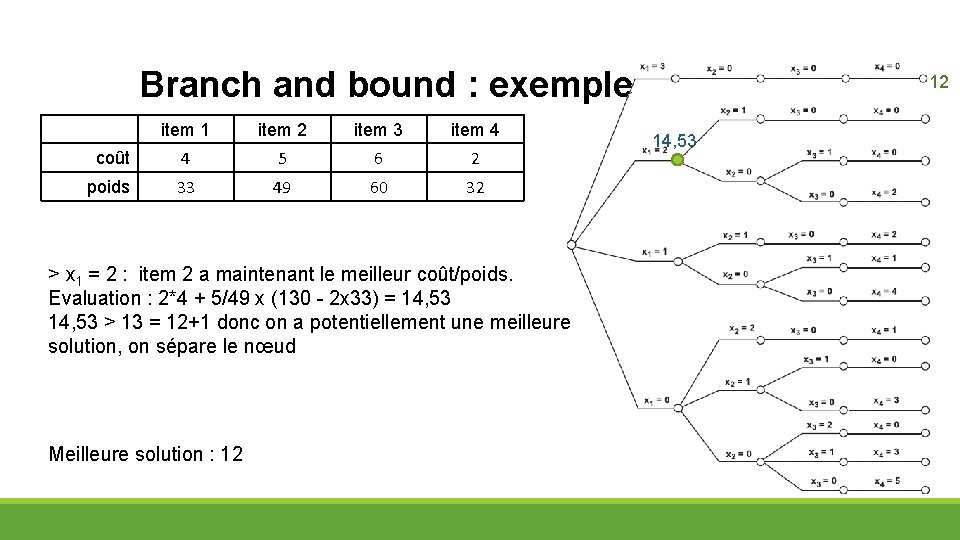
Branch and bound : exemple item 1 item 2 item 3 item 4 coût 4 5 6 2 poids 33 49 60 32 > x 1 = 2 : item 2 a maintenant le meilleur coût/poids. Evaluation : 2*4 + 5/49 x (130 - 2 x 33) = 14, 53 > 13 = 12+1 donc on a potentiellement une meilleure solution, on sépare le nœud Meilleure solution : 12 12 14, 53

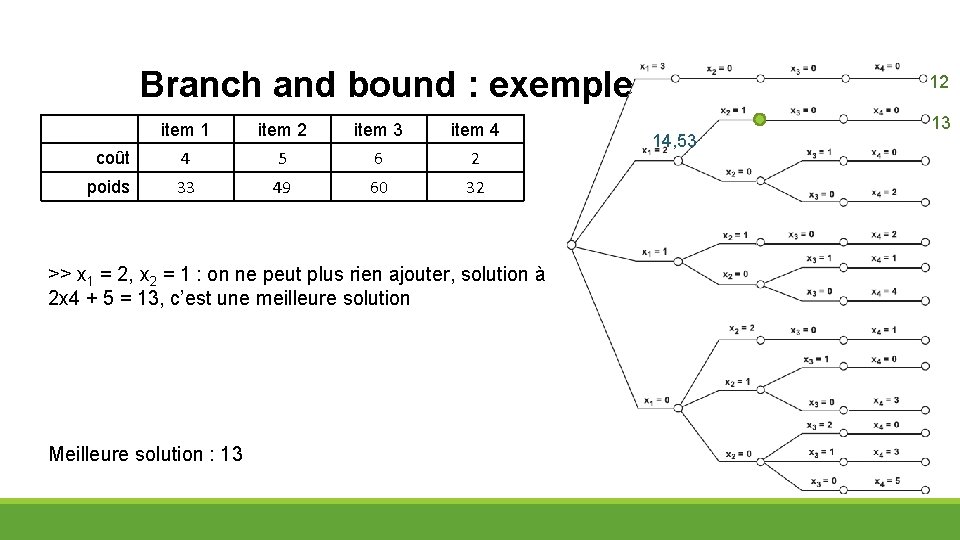
Branch and bound : exemple item 1 item 2 item 3 item 4 coût 4 5 6 2 poids 33 49 60 32 >> x 1 = 2, x 2 = 1 : on ne peut plus rien ajouter, solution à 2 x 4 + 5 = 13, c’est une meilleure solution Meilleure solution : 13 12 14, 53 13

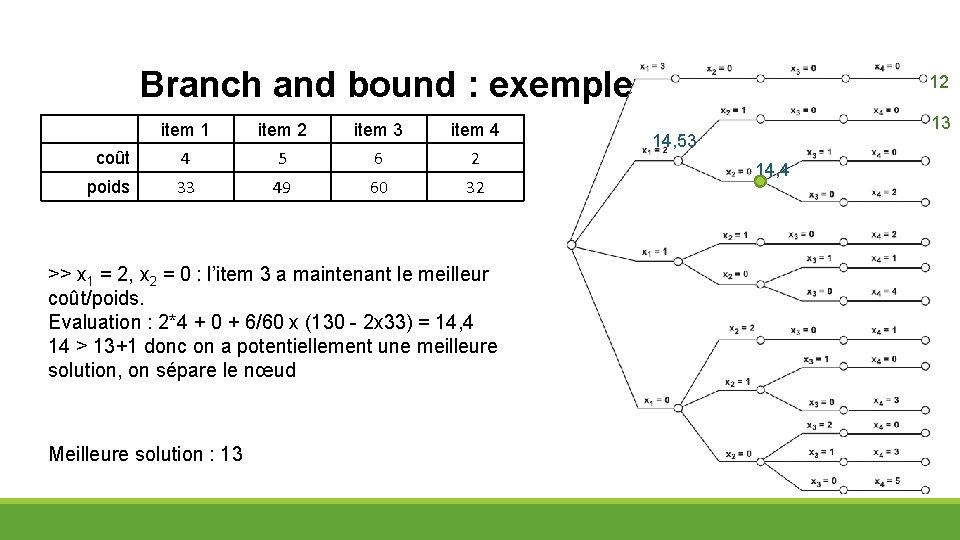
Branch and bound : exemple item 1 item 2 item 3 item 4 coût 4 5 6 2 poids 33 49 60 32 >> x 1 = 2, x 2 = 0 : l’item 3 a maintenant le meilleur coût/poids. Evaluation : 2*4 + 0 + 6/60 x (130 - 2 x 33) = 14, 4 14 > 13+1 donc on a potentiellement une meilleure solution, on sépare le nœud Meilleure solution : 13 12 13 14, 53 14, 4

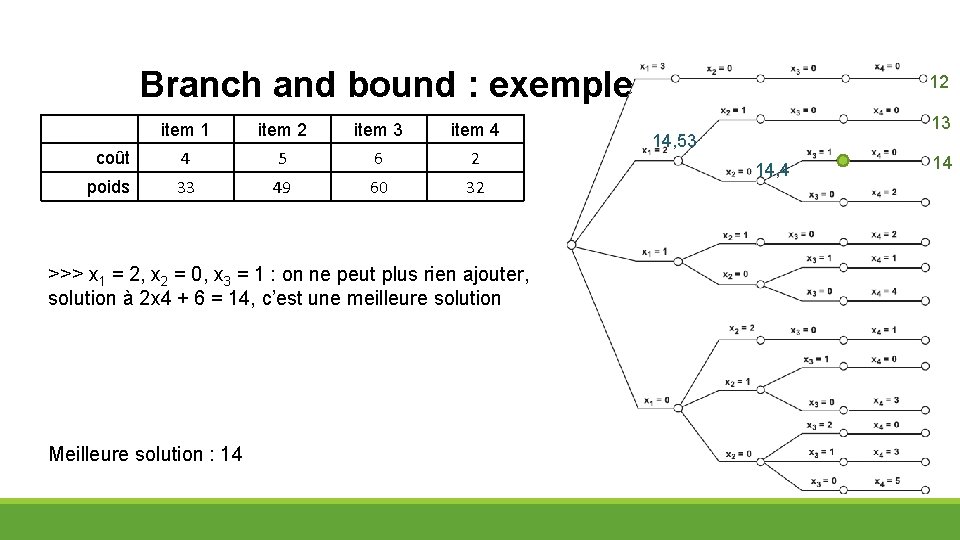
Branch and bound : exemple item 1 item 2 item 3 item 4 coût 4 5 6 2 poids 33 49 60 32 >>> x 1 = 2, x 2 = 0, x 3 = 1 : on ne peut plus rien ajouter, solution à 2 x 4 + 6 = 14, c’est une meilleure solution Meilleure solution : 14 12 13 14, 53 14, 4 14

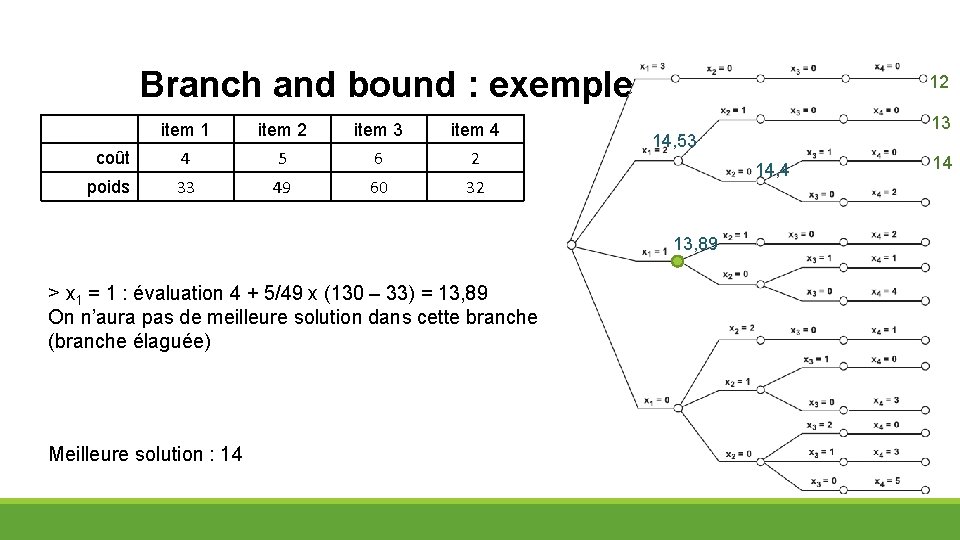
Branch and bound : exemple item 1 item 2 item 3 item 4 coût 4 5 6 2 poids 33 49 60 32 12 14, 53 14, 4 13, 89 > x 1 = 1 : évaluation 4 + 5/49 x (130 – 33) = 13, 89 On n’aura pas de meilleure solution dans cette branche (branche élaguée) Meilleure solution : 14 13 14

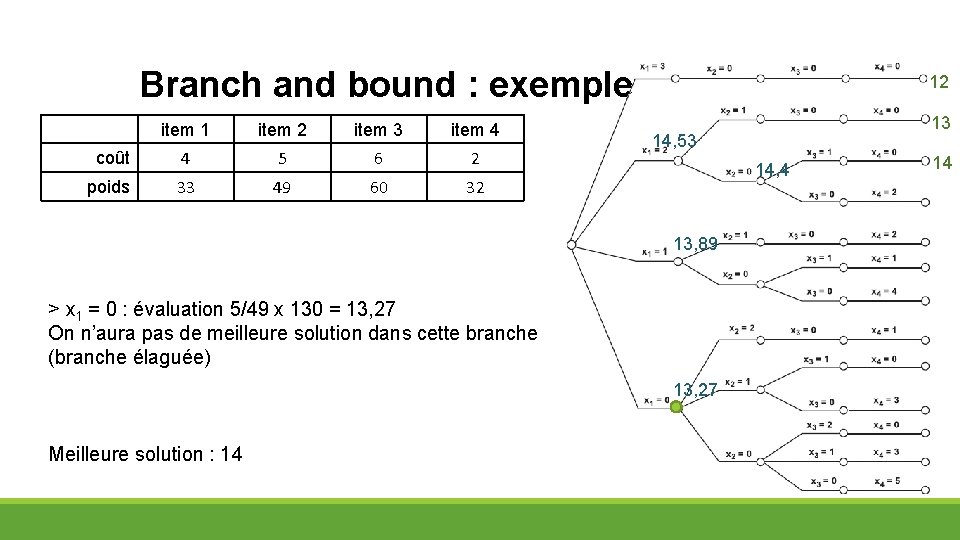
Branch and bound : exemple item 1 item 2 item 3 item 4 coût 4 5 6 2 poids 33 49 60 32 12 14, 53 14, 4 13, 89 > x 1 = 0 : évaluation 5/49 x 130 = 13, 27 On n’aura pas de meilleure solution dans cette branche (branche élaguée) 13, 27 Meilleure solution : 14 13 14

Branch and bound : algorithme function solve. BB(problem): | active. Nodes ← get. Active. Nodes(problem) | best ← -∞ | while active. Nodes != []: | | n = chose. Active. Node(active. Nodes) # à définir | | if est. Solution(n): # si c’est une solution, on met à jour le maximum | | | best ← max(best, n) | | else: | | | children ← split(n) # on récupère les fils du noeud qu’on étudie | | | for f in children: | | e ← eval(f) # à définir | | if e > best: # on explore la branche que si elle peut être meilleure | | | active. Nodes. add(f) | return best