Arbori binari Aplicaii Arbori binari Definiie Un arbore

Arbori binari. Aplicaţii

Arbori binari • Definiţie. Un arbore binar este un arbore orientat cu proprietatea că pentru orice vîrf v, od(v) 2. Dacă od(v)=2, cei doi descendenţi sînt desemnaţi ca descendent stîng (fiu stînga) respectiv descendent drept (fiu dreapta). Pentru vîrfurile cu od(v)=1, unicul descendent este specificat fie ca fiu stînga, fie ca fiu dreapta • Definiţie. Se numeşte arbore strict binar un arbore binar cu poprietatea că pentru orice vîrf v, od(v)≠ 1. • Definiţie. Se numeşte nod terminal (sau frunză) orice vîrf v al arborelui cu od(v)=0. În caz contrar nodul v este neterminal.
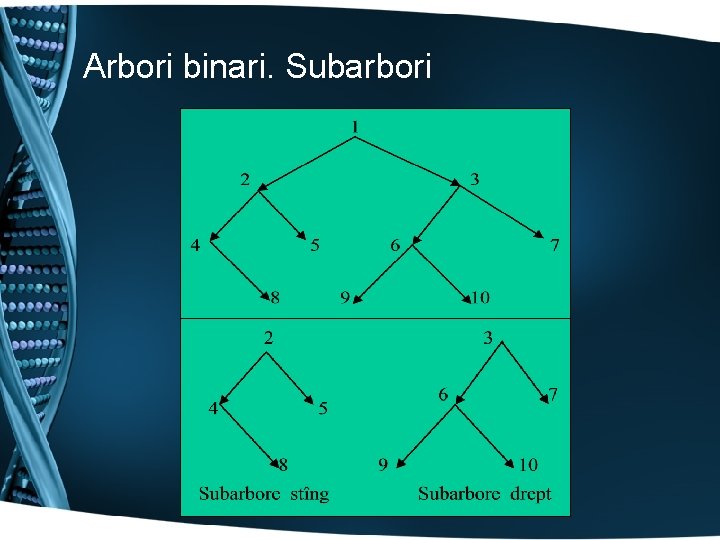
Arbori binari. Subarbori

Arbori binari. Reprezentare. • Reprezentarea Fiu-Frate (N, R, Fiu, Frate, Inf) • Cu structuri dinamice – Structură nod: informaţie, adresă fiu stîng / drept typedef struct nod { int info; struct nod* st, *dr; } TNOD; • Pentru a cunoaşte arborele: rădăcina TNOD* r;

Arbori binari. Parcurgere • În lăţime – Pe niveluri • În adîncime – A-Preordine – A-Postordine – Preordine Postordine Inordine void inordine(TNOD* void preordine(TNOD* r) void r) postordine(TNOD* r) { if(r!=NULL) { inordine(r->st); { //prelucrare r->info { postordine(r->st); //prelucrare r->info preordine(r->st); postordine(r->dr); inordine(r->dr); preordine(r->dr); //prelucrare r->info } } }

Arbori binari. Parcurgere typedef struct nodc void niveluri(TNOD* r) { TNOD* info; { TNODC* c; struct nodc* next; TNOD* p; } TNODC; int er; if(r != NULL) { c = NULL; c = push(c, r); while(c != NULL) { c=pop(c, &p, &er); // prelucrare p->info if(p->st!=NULL) c = push(c, p->st); if(p->dr!=NULL) c = push(c, p->dr); } } }

Arbori binari. Calculul înălţimii int inaltime(TNOD* r) { int i, j, k; if(r == NULL) i = 0; else { j = inaltime(r->st); k = inaltime(r->dr); i = 1 + (j>k ? j : k); } return(i); }

Arbori de sortare (căutare) • Definiţie. Un arbore de sortare este un arbore binar cu următoarele proprietăţi – fiecărui nod i al arborelui îi este ataşată o informaţie INF(i) dintr-o mulţime ordonată de valori; – pentru fiecare nod i, INF(i) este mai mare decît INF(j), pentru toate nodurile j din subarborele stîng al arborelui cu rădăcină i; – pentru fiecare nod i, INF(i) este mai mică decît INF(j), pentru toate nodurile j din subarborele drept al arborelui cu rădăcină i; – pentru orice vîrfuri i şi j daca i j atunci INF(i) INF(j).
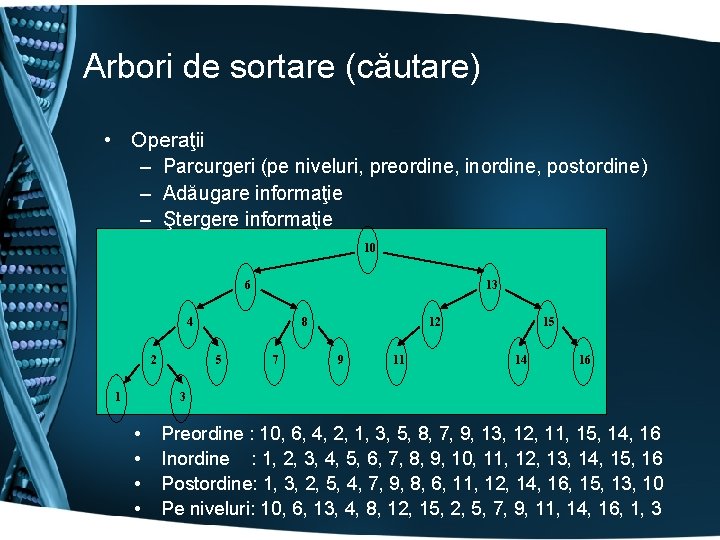
Arbori de sortare (căutare) • Operaţii – Parcurgeri (pe niveluri, preordine, inordine, postordine) – Adăugare informaţie – Ştergere informaţie 10 6 13 4 2 1 12 8 5 7 9 11 15 14 16 3 • • Preordine : 10, 6, 4, 2, 1, 3, 5, 8, 7, 9, 13, 12, 11, 15, 14, 16 Inordine : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 Postordine: 1, 3, 2, 5, 4, 7, 9, 8, 6, 11, 12, 14, 16, 15, 13, 10 Pe niveluri: 10, 6, 13, 4, 8, 12, 15, 2, 5, 7, 9, 11, 14, 16, 1, 3
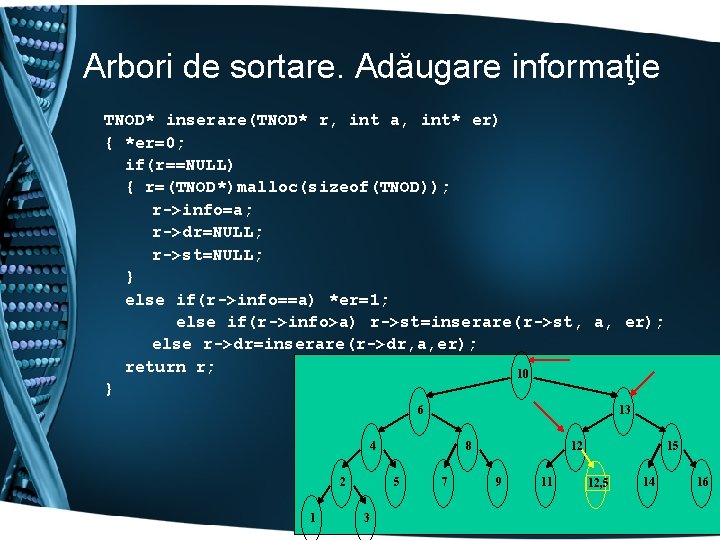
Arbori de sortare. Adăugare informaţie TNOD* inserare(TNOD* r, int a, int* er) { *er=0; if(r==NULL) { r=(TNOD*)malloc(sizeof(TNOD)); r->info=a; r->dr=NULL; r->st=NULL; } else if(r->info==a) *er=1; else if(r->info>a) r->st=inserare(r->st, a, er); else r->dr=inserare(r->dr, a, er); return r; 10 } 6 13 8 4 2 1 5 3 7 12 9 11 15 12, 5 14 16
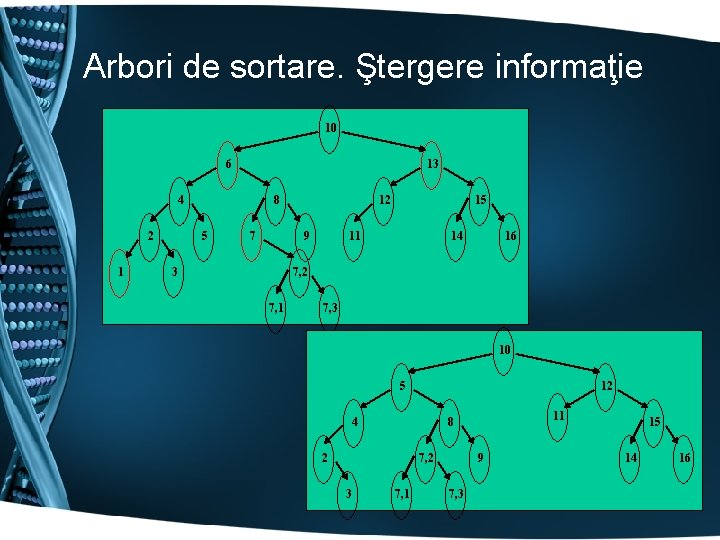
Arbori de sortare. Ştergere informaţie 10 6 13 4 2 1 12 8 5 7 9 3 15 11 14 16 7, 2 7, 1 7, 3 10 5 12 4 2 9 7, 2 3 11 8 7, 1 7, 3 15 14 16

Arbori de sortare. Ştergere informaţie TNOD* sterge(TNOD* r, int a, int*er) { TNOD* p, *q; *er=0; if(r == NULL) *er=1; else if(r->info > a) r->st = sterge(r->st, a, er); else if(r->info < a) r->dr = sterge(r->dr, a, er); else if(r->st == NULL) { p = r; r = r->dr; free(p); } else if(r->st->dr==NULL) { r->info = r->st->info; p = r->st; r->st = r->st; free(p); } else { p = r->st; while(p->dr != NULL) { q = p; p = p->dr; } r->info = p->info; q->dr = p->st; free(p); } return r; }

Arbori de structură • Arbore de structură: arbore strict binar folosit pentru a reprezenta expresiile aritmetice care conţin numai operatori binari. Fiecare nod conţine ca informaţie utilă: – un operand, dacă este nod frunză – un operator, dacă nu e nod frunză • Arborele se construieşte acordînd priorităţi operanzilor şi operatorilor. • Parcurgerea arborelui în preordine => forma poloneză directă a expresiei • Parcurgere arborelui în inordine => refacerea expresiei (cu sau fără paranteze).
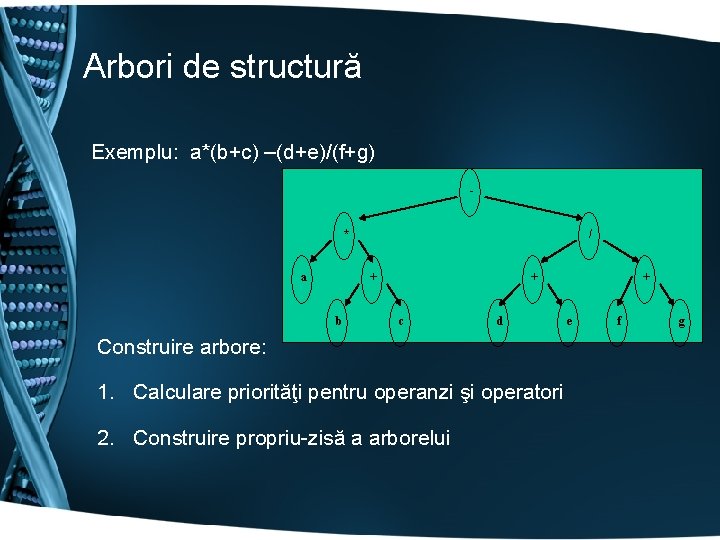
Arbori de structură Exemplu: a*(b+c) –(d+e)/(f+g) - / * + + a b c d Construire arbore: 1. Calculare priorităţi pentru operanzi şi operatori 2. Construire propriu-zisă a arborelui + e f g

Arbori de structură Exemplu: a*(b+c) –(d+e)/(f+g) 1. Calculare priorităţi pentru operanzi şi operatori • operatorii aditivi primesc prioritatea 1 • operatorii multiplicativi primesc prioritatea 10 • prioritatea fiecărui operator se măreşte cu 10 pentru fiecare pereche de paranteze care îl include • fiecare operand primeşte prioritatea maximă (maxint) Priorităţile sînt înscrise într-un vector. • p[i]= prioritatea elementului i din expresie (operator sau operand, în ordinea apariţiei Elemente expr. =( Priorităţi a, *, b, +, c, -, d, +, e, /, f, +, g) =(maxint, 10, maxint, 11, maxint)

Arbori de structură Exemplu: a*(b+c) –(d+e)/(f+g) Elemente expr. =( Priorităţi a, *, b, +, c, -, d, +, e, /, f, +, g) =(maxint, 10, maxint, 11, maxint) Construire arbore: algoritm recursiv. 1. dacă expresia curentă este vidă, subarborele curent este vid (nil) 2. altfel se caută elementul cu prioritate minimă din expresia curentă 3. se creează un nod rădăcină pentru subarborele curent 4. fiul stîng este subarborele obţinut prin reprezentarea subexpresiei din stînga elementului curent 5. fiul drept este subarborele obţinut prin reprezentarea subexpresiei din dreapta elementului curent
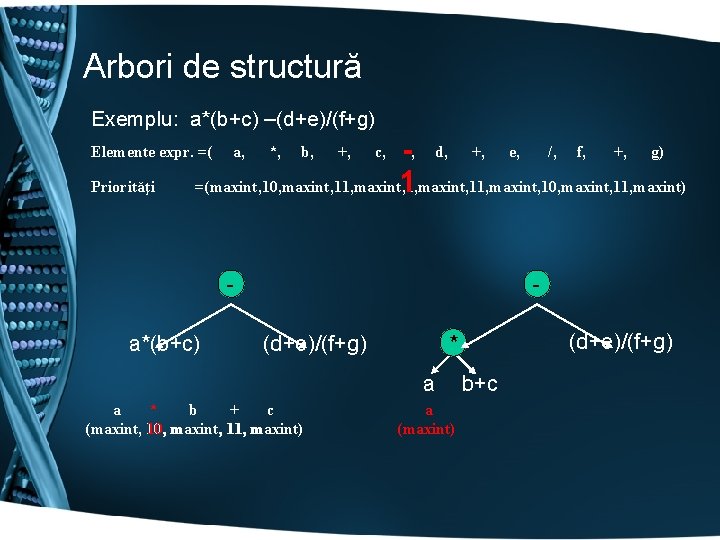
Arbori de structură Exemplu: a*(b+c) –(d+e)/(f+g) --, d, +, e, /, f, +, g) =(maxint, 10, maxint, 11, maxint) 1 Elemente expr. =( Priorităţi a, *, b, +, c, a*(b+c) - a a * b + c (maxint, 10, maxint, 11, maxint) (d+e)/(f+g) * (d+e)/(f+g) a (maxint) b+c
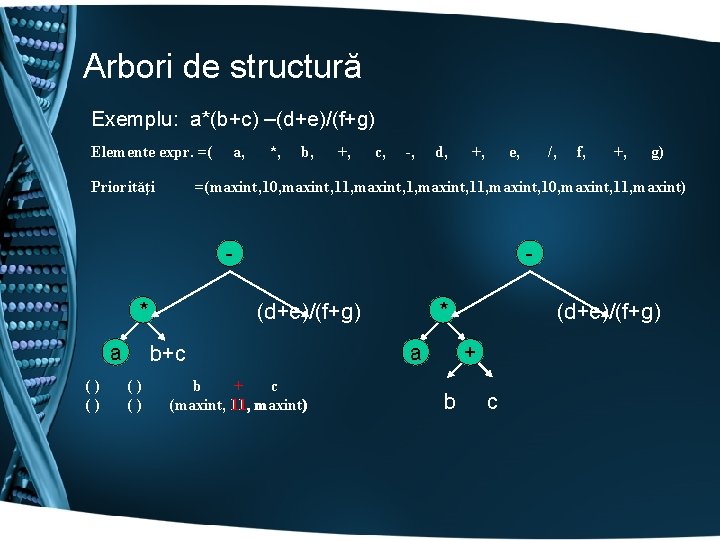
Arbori de structură Exemplu: a*(b+c) –(d+e)/(f+g) Elemente expr. =( Priorităţi a, *, b, +, c, -, d, +, e, * () () +, g) * (d+e)/(f+g) b+c () () f, =(maxint, 10, maxint, 11, maxint) - a /, b + c (maxint, 11, maxint) a (d+e)/(f+g) + b c
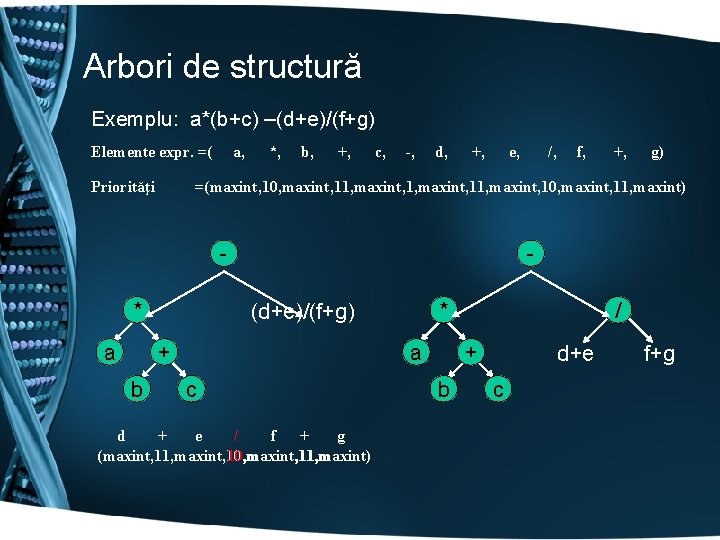
Arbori de structură Exemplu: a*(b+c) –(d+e)/(f+g) Elemente expr. =( Priorităţi a, *, b, +, c, -, d, +, e, * +, g) * (d+e)/(f+g) + b f, =(maxint, 10, maxint, 11, maxint) - a /, + a c d + e / f + g (maxint, 11, maxint, 10, maxint, 11, maxint) / b d+e c f+g

Arbori de structură Parcurgerea arborelui în preordine => forma poloneză directă a expresiei: -*a+bc/+de+fg Parcurgere arborelui în inordine => refacerea expresiei (cu sau fără paranteze – SRD sau (S)R(D) ): a*b+c–d+e/f+g ((a)*((b)+(c)))-(((d)+(e))/((f)+(g)))

Arbori de structură Evaluare expresie: prin parcurgere în postordine. Prelucrarea fiecărui nod r constă în • dacă e nod frunză nu se schimbă nimic • altfel se înlocuieşte informaţia r->inf cu rezultatul expresiei ss r->inf sd unde ss şi sd sînt informaţiile din fiul stîng respectiv drept al nodului curent
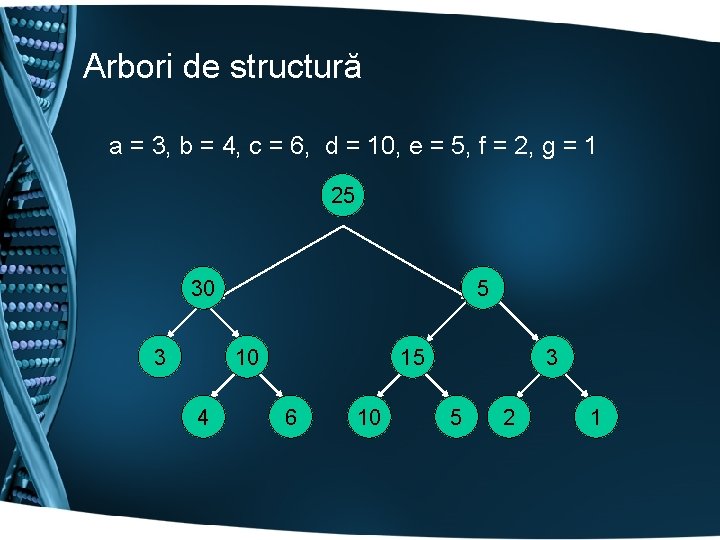
Arbori de structură a = 3, b = 4, c = 6, d = 10, e = 5, f = 2, g = 1 25 - 30 * 3 5/ + 10 4 + 15 6 10 + 3 5 2 1

Arbori de structură - implementare #include <stdio. h> #include <malloc. h> #include <string. h> #include <math. h> #define MAXINT 10000 /* reprezentarea unei expresii prin arbore de structura si evaluarea ei restrictii: - numai operatori aritmetici + - * / - identificatorii operanzilor formati din numai o litera - fara spatii */ typedef struct nod{ char inf; float v; struct nod *s, *d; } TNOD;
![Arbori de structură - implementare char* prioritati(char *s, int p[], int* n) { int Arbori de structură - implementare char* prioritati(char *s, int p[], int* n) { int](http://slidetodoc.com/presentation_image_h/2ede2dafa9e09376c7d46667a5dcab29/image-24.jpg)
Arbori de structură - implementare char* prioritati(char *s, int p[], int* n) { int i, j, crt, l; char* r; //i - caracterul curent //j - proritatea curenta //crt - elementul curent //r - expresia fara paranteze //calcul prioritati l = strlen(s); for(i=j=crt=0; i<l; i++) switch(s[i]) { case ')': j-=10; break; case '(': j+=10; break; case '+': ; case '-': p[crt]=j+1; crt++; break; case '*': ; case '/': p[crt]=j+10; crt++; break; default : p[crt++]=MAXINT; }
![Arbori de structură - implementare //eliminare paranteze r=(char*)malloc(strlen(s)); strcpy(r, s); i=0; while(i<l) if( (r[i]==')') Arbori de structură - implementare //eliminare paranteze r=(char*)malloc(strlen(s)); strcpy(r, s); i=0; while(i<l) if( (r[i]==')')](http://slidetodoc.com/presentation_image_h/2ede2dafa9e09376c7d46667a5dcab29/image-25.jpg)
Arbori de structură - implementare //eliminare paranteze r=(char*)malloc(strlen(s)); strcpy(r, s); i=0; while(i<l) if( (r[i]==')') || (r[i]=='(') ) { for(j=i+1; j<l; j++) r[j-1]=r[j]; r[l]='�'; l--; } else i++; *n=crt; return r; }
![Arbori de structură - implementare TNOD* construire_arbore(int p, int u, char *r, int pr[]) Arbori de structură - implementare TNOD* construire_arbore(int p, int u, char *r, int pr[])](http://slidetodoc.com/presentation_image_h/2ede2dafa9e09376c7d46667a5dcab29/image-26.jpg)
Arbori de structură - implementare TNOD* construire_arbore(int p, int u, char *r, int pr[]) { TNOD *a; int min, poz; min = pr[p]; poz = p; for(int i=p+1; i<=u; i++) if(min >= pr[i]) { min=pr[i]; poz=i; } a=(TNOD*)malloc(sizeof(TNOD)); a->inf = r[poz]; if(p == u) a->s = a->d = NULL; else { a->s = construire_arbore(p, poz-1, r, pr); a->d = construire_arbore(poz+1, u, r, pr); } return a; }

Arbori de structură - implementare void forma_poloneza(TNOD* rad, char* exp) { int l; if(rad) { l = strlen(exp); exp[l] = rad->inf; exp[l+1] = '�'; forma_poloneza(rad->s, exp); forma_poloneza(rad->d, exp); } }

Arbori de structură - implementare float evaluare(TNOD* rad) { if(rad) if(rad->s) switch (rad->inf) { case '+': rad->v = break; case '-': rad->v = break; case '*': rad->v = break; case '/': rad->v = } return rad->v; } evaluare(rad->s) + evaluare(rad->d); evaluare(rad->s) - evaluare(rad->d); evaluare(rad->s) * evaluare(rad->d); evaluare(rad->s) / evaluare(rad->d);

Arbori de structură - implementare void citire_valori_operanzi(TNOD* rad) { if(rad) if(rad->s == NULL) { printf("%c=", rad->inf); scanf("%f", &(rad->v)); } else { citire_valori_operanzi(rad->s); citire_valori_operanzi(rad->d); } }
![Arbori de structură - implementare void main() { char expresie[100], *efp, *fpd; int p[100], Arbori de structură - implementare void main() { char expresie[100], *efp, *fpd; int p[100],](http://slidetodoc.com/presentation_image_h/2ede2dafa9e09376c7d46667a5dcab29/image-30.jpg)
Arbori de structură - implementare void main() { char expresie[100], *efp, *fpd; int p[100], n; TNOD* radacina_arbore_structura; printf("n. Expresia de analizat (corecta, conform restrictiilor): n"); gets(expresie); radacina_arbore_structura=NULL; //calcul prioritati efp=prioritati(expresie, p, &n); //construire arbore radacina_arbore_structura=construire_arbore(0, n-1, efp, p); //determinarea formei poloneze a expresiei fpd=(char*)malloc(strlen(efp)); fpd[0]='�'; forma_poloneza(radacina_arbore_structura, fpd); printf("n. Forma poloneza directa: %s", fpd); //evaluare expresie printf("n. Valorile operanzilor: n"); citire_valori_operanzi(radacina_arbore_structura); evaluare(radacina_arbore_structura); printf("n. Valoare expresiei este: %7. 3 fn", radacina_arbore_structura>v); }

Arbori de structură - implementare • Atenţie: – Dacă mai multe elemente au aceeaşi prioritate minimă, se alege ultimul pentru a fi rădăcină – Exemplu: – a-b*c+d – a=100, b=2, c=5, d=10 • Probleme de rezolvat – Eliminarea spaţiilor – Utilizarea altor operatori – Utilizarea de identificatori mai lungi
- Slides: 31