Aqueous Equilibria Followup Titration Curves To identify weak

Aqueous Equilibria Follow-up

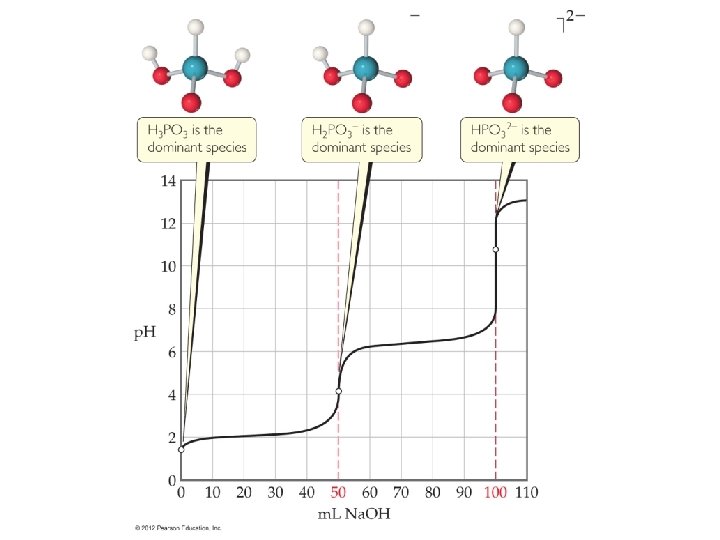
Titration Curves • To identify weak acids we can use p. Ka which can be determined from the graph. • Ka = [H 3 O+][A-] [HA] • We can get Ka = [H 3 O+] if we measure when the [A -] = [HA] • At that point the p. Ka = p. H • Strong base will remove the stoichiometric equivalent of acid, so the equivalence point will be where the amount of base added is equal to the amount of acid at the start.

p. Ka • The point at which the [A-] = [HA] is when we have reacted half the acid with the strong base. • So this is half way to the equivalence point. • So if you get the p. H when half of the volume of base is added that was necessary to get to the equivalence point, that is equal to the p. Ka. • To find the equivalence point on the graph you can find the inflection point (2 nd derivative) to see where the graph changes is direction of the curve. • The second inflection point is going to require the same volume of base that the first inflection point required.

Common Ion Problem • Calculate the p. H of a solution that is 0. 60 M HF and 1. 00 M KF. • Ka = 7. 2 x 10 -4 for HF.

Solution • Major species: HF, K+, F-. There will be very little H+ since HF is weak. • The reaction is HF + H 2 O ↔ H 3 O+ + FHF H 3 O+ F- I 0. 60 0 1. 00 C -x +x +x E 0. 60 -x +x 1. 00+x • 7. 2 x 10 -4 = (1+x)(x)/(0. 60 -x) • Assume both x’s are small in reference to the 0. 60 M and 1. 00 M.

Completion of Problem • So 7. 2 x 10 -4 = 1 x/0. 60 • x = 4. 3 x 10 -4 = [H 3 O+] • p. H = -log [H 3 O+] = 3. 37

You try! • What is the p. H of a solution made by adding 0. 30 mol of acetic acid and 0. 20 mol of sodium acetate to enough water to make 1. 0 L of solution? • Ka for acetic acid = 1. 8 x 10 -5 p. H = 4. 56

Buffers • Buffered solutions can be made in 2 ways. • 1) Adding a salt that has the common conjugate ion to the weak acid or base. • 2) Adding a strong acid/base to the weak base/acid solution to create the common ion. • The buffer capacity is related to how much can be added to the solution before the p. H is effected. • The capacity is increased as the concentration is increased, and increases as the ratio of the conjugates gets closer to 1.

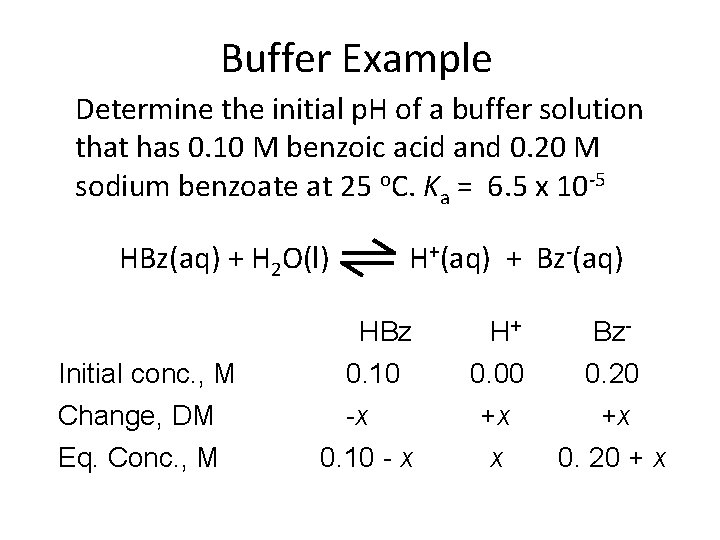
Buffer Example Determine the initial p. H of a buffer solution that has 0. 10 M benzoic acid and 0. 20 M sodium benzoate at 25 o. C. Ka = 6. 5 x 10 -5 HBz(aq) + H 2 O(l) H+(aq) + Bz-(aq) HBz Initial conc. , M 0. 10 Change, DM -x Eq. Conc. , M 0. 10 - x H+ Bz- 0. 00 0. 20 +x +x x 0. 20 + x

Buffer Example Solve the equilibrium equation in terms of x Ka = 6. 5 x x 10 -5 x (0. 20 + x) = 0. 10 - x = (6. 5 x 10 -5 )(0. 10) / (0. 20) (assuming x<<0. 10) = 3. 2 x 10 -5 M H+ p. H = - log (3. 2 x 10 -5 M) = 4. 5 initial p. H

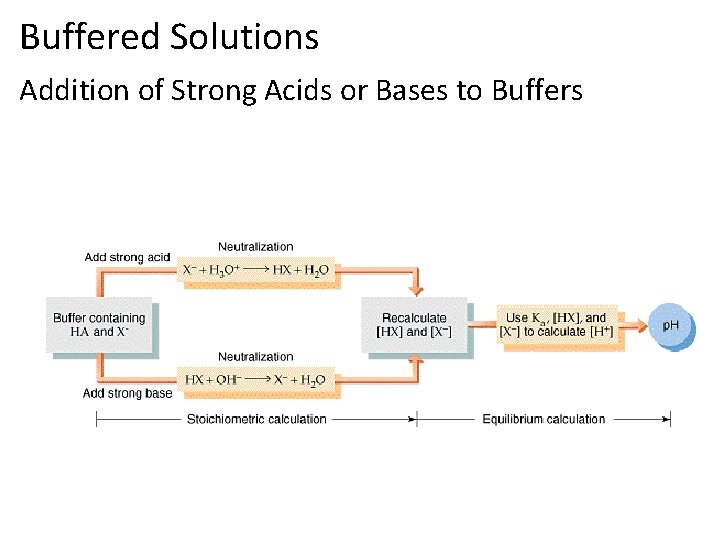
Buffered Solutions Addition of Strong Acids or Bases to Buffers

Buffer Example Determine the p. H of a buffer solution that has 0. 10 M benzoic acid and 0. 20 M sodium benzoate at 25 o. C after 0. 05 moles of HCl is added. Total volume of solution is 1 L. First, find the concentrations of the HBz and Bz- after HCl is added. Initial conc. , M Change, DM Eq. Conc. , M HBz 0. 15 -x 0. 15 - x x H+ Bz 0. 00 0. 15 +x +x 0. 15 + x The 0. 05 mol HCl reacts completely with 0. 05 mol Bz-(aq) to form 0. 05 mol HBz(aq) Then equilibrium will be re-established based on the new initial concentrations of 0. 15 M HBz(aq) and 0. 15 M Bz-(aq).

Buffer Example Solve the equilibrium equation in terms of x x (0. 15 + x) -5 Ka = 6. 5 x 10 = 0. 15 - x x = (6. 5 x 10 -5 )(0. 15) / (0. 15) (assuming x<<0. 15) = 6. 5 x 10 -5 M H+ p. H = - log (6. 5 x 10 -5 M) = 4. 2 after 0. 05 mole HCl added

Buffer Example Determine the p. H of a buffer solution that has 0. 10 M benzoic acid and 0. 20 M sodium benzoate at 25 o. C after 0. 05 moles of Na. OH is added.

Solution • First, find the concentrations of HBz and Bz- after Na. OH is added. • The 0. 05 mol Na. OH reacts completely with 0. 05 mol HBz(aq) to form 0. 05 mol Bz-(aq) • Then equilibrium will be re-established based on the new initial concentrations of 0. 05 M HBz(aq) and 0. 25 M Bz-(aq). HBz H+ Bz- I 0. 05 0. 00 0. 25 C -x +x +x E 0. 05 - x x 0. 25 + x

Buffer Example Solve the equilibrium equation in terms of x Ka = 6. 5 x 10 -5 = x (0. 25 + x) 0. 05 - x x = (6. 5 x 10 -5 )(0. 05) / (0. 25) (assuming x<<0. 05) = 1. 3 x 10 -5 M H+ p. H = - log (1. 3 x 10 -5 M) = 4. 9 after 0. 05 mole Na. OH added

Making a Buffer Calculations You want to prepare 500. 0 m. L of a buffer with a p. H = 10. 00, with both the acid and conjugate base having molarities between 0. 10 M to 1. 00 M. You may choose from any of the acids listed below: You must select an acid with a Ka value close to 10 assigned p. H. The only two options are ammonium or the hydrogen carbonate ions.

Making a Buffer Calculations Lets use concentrated NH 3 which is 14. 8 M and ammonium chloride.

Finish • Place ~250 m. L of distilled water in a 500 m. L volumetric flask. Add 2. 68 g NH 4 Cl and dissolve. Then mix in 18. 9 m. L of 14. 8 M NH 3. Fill with distilled water to the 500 m. L mark on the flask.

Making a Buffer Calculations If there is no concentrated NH 3 available, the NH 3 can be produced by neutralizing additional NH 4 Cl with 1. 00 M Na. OH.

Solution Dissolve 17. 66 g NH 4 Cl (2. 68 g + 14. 98 g) in 280. m. L of 1. 00 M Na. OH. Then dilute with distilled water and fill to the 500 m. L mark on the flask.

Making a Buffer Calculations If there is no NH 4 Cl available, the NH 4+ can be produced by neutralizing additional NH 3 with 1. 00 M HCl.

Solution Place ~250 m. L distilled water in volumetric flask. Add 50. 0 m. L of 1. 00 M HCl and mix. Then add 22. 3 m. L of concentrated NH 3 (18. 9 m. L + 3. 4 m. L). Mix and fill with distilled water to the 500 m. L mark on the flask.

Making a Buffer Calculations Prepare 500. m. L of the buffer that has [CO 32 -] = 0. 100 M and [HCO 31 -] = 0. 179 M.

Making a Buffer Calculations Place ~250 m. L distilled water in a 500 m. L volumetric flask. Add 5. 30 g Na 2 CO 3 and 7. 52 g Na. HCO 3 and dissolve. Fill with distilled water to the 500 m. L mark on the flask.

Acetic Acid/Acetate Ion Buffer Lab For this experiment, you will prepare a buffer that contains acetic acid and its conjugate base, the acetate ions. The equilibrium equation for the reaction is shown below: HC 2 H 3 O 2(aq) + H 2 O(l) <=> H+ (aq)+ C 2 H 3 O 2 - (aq) The equilibrium expression for this reaction, Ka, has a value of 1. 8 x 10 -5 at 25ºC.

Acetic Acid/Acetate Ion Buffer Lab · The ratio between the molarity of the acetate ions to the molarity of the acetic acid in your buffer must equal the ratio between the Ka value and 10 - assigned p. H. · This ratio should be reduced , so that either the [HC 2 H 3 O 2] or [C 2 H 3 O 2 - ] has a concentration of 0. 10 M, and the concentration of the other component must fall within a range from 0. 10 M to 1. 00 M. · Complete the calculations only that are needed to prepare 100. 0 m. L of your assigned buffer solution that has these specific concentrations. Can you predict the final p. H when a strong acid or base is added to the buffer solution?

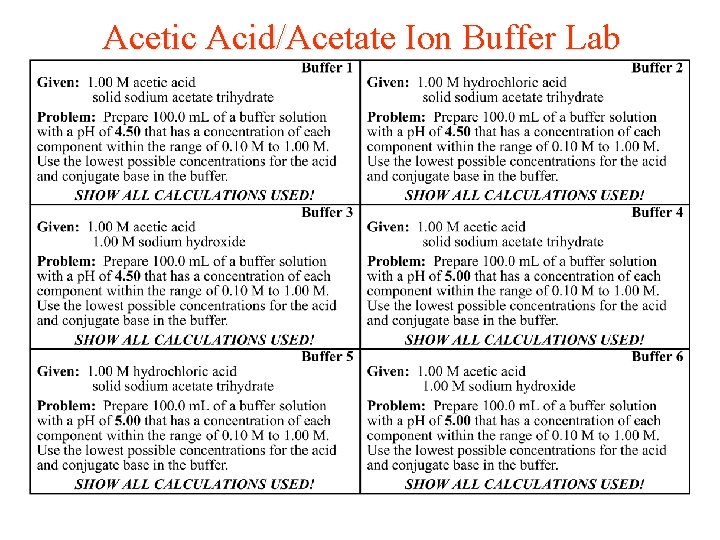
Acetic Acid/Acetate Ion Buffer Lab

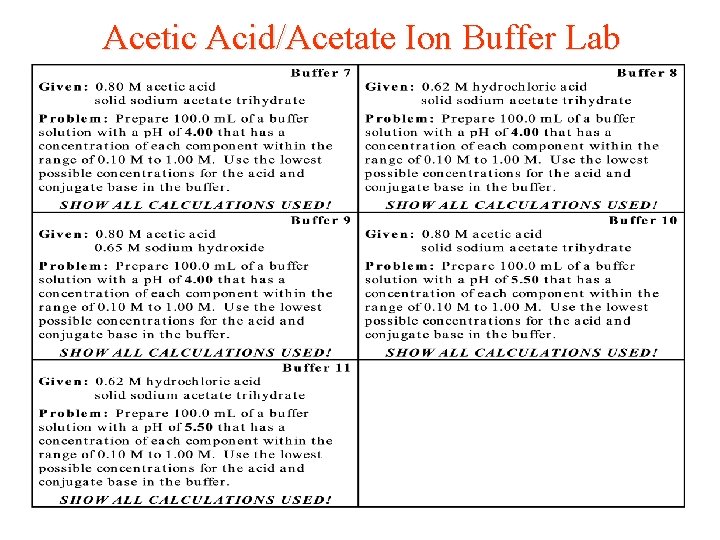
Acetic Acid/Acetate Ion Buffer Lab

Buffer Answers 1 -6 • • • 1) 1. 36 g Na. C 2 H 3 O 2 and 17 m. L of HC 2 H 3 O 2 2) 3. 76 g HC 2 H 3 O 2 and 17 m. L of HCl 3) 27. 0 m. L HC 2 H 3 O 2 and 10 m. L Na. OH 4) 2. 45 g Na. C 2 H 3 O 2 and 10 m. L HC 2 H 3 O 2 5) 3. 81 g Na. C 2 H 3 O 2 and 10 m. L HCl 6) 28 m. L HC 2 H 3 O 2 and 18 m. L Na. OH

Buffer Answers 7 -11 • • • 7) 2. 45 g Na. C 2 H 3 O 2 and 70. 0 m. L HC 2 H 3 O 2 8) 10. 07 g Na. C 2 H 3 O 2 and 90. 3 m. L HCl 9) 82. 5 m. L HC 2 H 3 O 2 and 15. 4 m. L Na. OH 10) 7. 89 g Na. C 2 H 3 O 2 and 12. 5 m. L HC 2 H 3 O 2 11) 9. 25 g Na. C 2 H 3 O 2 and 16. 1 m. L HCl

Ksp • The equilibrium is established when the solution is saturated. • The only way to know when the solution is saturated is to observe solid in the bottom of the beaker. • Calculate the silver ion concentrations in saturated solutions of silver chloride (Ksp = 1. 8 x 1010) and silver sulfate (K = 1. 5 x 10 -5) sp

Answers • 1. 8 x 10 -10 = [x][x] • [Ag+] = 1. 34 x 10 -5 M • 1. 5 x 10 -5 = [2 x]2[x] • [Ag+] = 0. 311 M

Common Ion Ksp Problem • What is the concentration of silver ions and chromate ions in a solution with solid silver chromate is added to a container with 0. 1 M silver nitrate? Ksp = 9 x 10 -12

Answer Ag 2 Cr. O 4(s) 2 Ag+1 + Cr. O 4 -2 I 0. 1 0 C +2 x +x E 0. 1 + 2 x x Ksp = 9. 0 x 10 -12 = [Ag+1]2 • [Cr. O 4 -2] = 9. 0 x 10 -12 = [. 1 +2 x]2 • [x] 9. 0 x 10 -12 = 0. 12 • x [Cr. O 4 -2] = x = 9. 0 x 10 -10 M [Ag+1] =. 1 + 2 x =. 1 M [Ag 2 Cr. O 4] = 9. 0 x 10 -10

A solution prepared by adding 750 m. L of 4. 00 x 10 -3 M Ce(NO 3)3 to 300. 0 m. L of 2. 00 x 10 -2 M KIO 3. Will Ce(IO 3)3 precipitate? (Ksp = 1. 9 x 10 -10) • Step one: Calculate the concentration of Ce+3 and IO 3 -1 before a reaction occurs [Ce+3]0 = (750. 0 m. L)(4. 00 x 10 -3 M) = 2. 86 x 10 -3 M (750. + 300. m. L) [IO 3 -1]0 = (300. 0 m. L)(2. 00 x 10 -3 M) = 5. 71 x 10 -3 M (750. + 300. m. L) Q = (2. 86 x 10 -3 M) x (5. 71 x 10 -3 M)3 = 5. 32 x 10 -10 Q > Ksp therefore the precipitation reaction will occur

Precipitation and Separation of Ions • At any instant in time, Q = [Ba 2+][SO 42 -]. – If Q < Ksp, precipitation occurs until Q = Ksp. – If Q = Ksp, equilibrium exists. – If Q > Ksp, solid dissolves until Q = Ksp. • Based on solubilities, ions can be selectively removed from solutions. • Consider a mixture of Zn 2+(aq) and Cu 2+(aq). Cu. S (Ksp= 6 10 -37) is less soluble than Zn. S(Ksp=2 10 -25), Cu. S will be removed from solution before Zn. S.

Precipitation and Separation of Ions • As H 2 S is added to the green solution, black Cu. S forms in a colorless solution of Zn 2+(aq). • When more H 2 S is added, a second precipitate of white Zn. S forms. Selective Precipitation of Ions • Ions can be separated from each other based on their salt solubilities. • Example: if HCl is added to a solution containing Ag+ and Cu 2+, the silver precipitates(Ksp for Ag. Cl is 1. 8 10 -10) while the Cu 2+ remains in solution, since Cu. Cl 2. • Removal of one metal ion from a solution is called selective precipitation.

Factors that Affect Solubility • • Presence of a common ion. p. H Formation of complex ions Amphoterism