Apsidal Angles Precession Brief Discussion Particle undergoing bounded

Apsidal Angles & Precession • Brief Discussion! • Particle undergoing bounded, non-circular motion in a central force field Always have r 1 < r 2 • V(r) vs r curve Only 2 apsidal distances exist for bounded, noncircular motion.

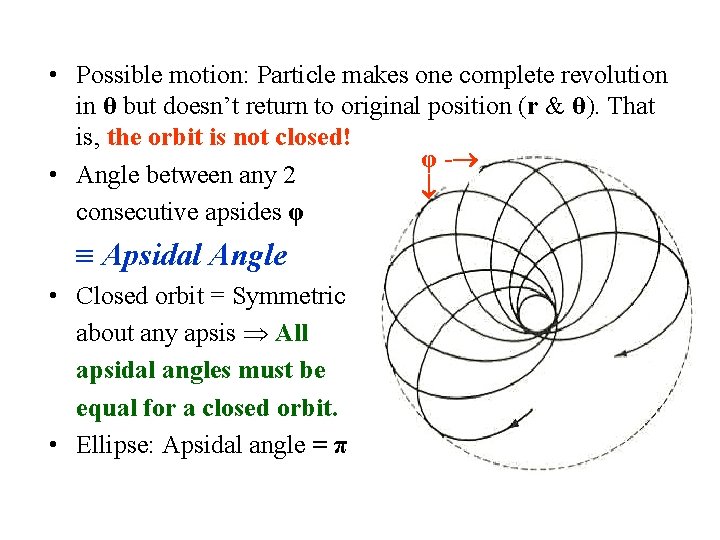
• Possible motion: Particle makes one complete revolution in θ but doesn’t return to original position (r & θ). That is, the orbit is not closed! φ - • Angle between any 2 consecutive apsides φ Apsidal Angle • Closed orbit = Symmetric about any apsis All apsidal angles must be equal for a closed orbit. • Ellipse: Apsidal angle = π

• If the orbit is not closed The mass gets to apsidal distances at different θ in each revolution Apsidal angle is not a rational fraction of 2π. • If the orbit is almost closed Apsides Precess Rotate Slowly in the plane of motion. • 1/r 2 force All elliptic orbits must be EXACTLY closed! The apsides must stay fixed in space for all time. • If the apsides move with time, no matter how slowly Force law is not exactly the inverse square law! Newton: “Advance or regression of a planet’s perihelion would require deviation of the force from 1/r 2. ” A sensitive test of Newton’s Law of Gravitation!

Precession • FACT: Planetary motion: Total force experienced by a planet deviates from 1/r 2 (r measured from sun), because of perturbations due to gravitational attractions to other planets, etc. For most planets, this effect is very small. Celestial (classical) dynamics calculations: Account for this (very accurately!) by perturbation theory. • Largest effect is for Mercury: Observed perihelion advances 574 of arc length PER CENTURY! • Accurate classical dynamics calculations using perturbation theory, as mentioned, predict 531 of arc length per century! 1° = 60´ = 3600´´ 574´´ 0. 159° 531´´ 0. 1475°

• Discrepancy between observation & classical dynamics calculations: 574 - 531 = 43 ( 0. 01194°) of arc length per century! Neither calculational nor observational uncertainties can account for this difference! Until early 1900’s this was the major outstanding difficulty with Newtonian Theory! • Einstein in early 1900’s: Showed that General Relativity (GR) accounts (VERY WELL) for this difference! A major triumph of GR! • Instead of doing GR, we can approximately account for this by (in ad-hoc manner) by inserting GR (plus Special Relativity) effects into Newtonian equations.

• Back a few lectures: General central force f(r): Differential eqtn which for orbit u(θ) 1/r(θ) (replacing mass μ with the planetary mass m): (d 2 u/dθ 2) + u = - (m/ 2)u-2 f(1/u) (1) Alternatively: (d 2[1/r]/dθ 2) + (1/r) = - (m/ 2)r 2 F(r) Put the universal gravitation law into this: fg(r) = -(GMm)/(r 2) & get: (d 2 u/dθ 2) + u = (Gm 2 M)/( 2) (2) • GR (+ SR) modification of (2) (lowest order in 1/c 2, c = speed of light): Add additional force to Fg(r) varying as (1/r 4) = u 4 : FGR(r) = -(3 GMm 2)/(c 2 r 4) = -(3 GMm 2)u 4/(c 2) • Put Fg(r) + FGR(r) into (1):

(2) is replaced by: (d 2 u/dθ 2) + u = (Gm 2 M)/( 2) + (3 GM)u 2/(c 2) (3) • Let: (1/α) (Gm 2 M)/( 2), δ (3 GM)/(c 2) (3) becomes: (d 2 u/dθ 2) + u = (1/α) + δu 2 (4) • Now some math to get an approximate soln to (4): (Like a nonlinear harmonic oscillator eqtn!) • Note: The nonlinear term δu 2 is very small, since δ (1/c 2) Use perturbation theory as outlined on pages 319320 of Marion (handed out in class!)

• After a lot of work (!), find the apsidal angle (perihelion precession) of θ = (2π)/[1 -(δ/α)] (2π)[1+(δ/α)] Effect of the GR term is to displace the perihelion in each revolution by Δ 2π(δ/α) = 6π[(Gm. M)/(c )]2 (5) • Results for elliptic orbit (μ = m): e = eccentricity, 2 = mka(1 - e 2); k = GMm, a = semimajor axis (5) becomes: Δ [6πGM]/[ac 2(1 - e 2)] (6)

• Prediction for an elliptic orbit, e = eccentricity, a = semimajor axis Δ [6πGM]/[ac 2(1 - e 2)] (6) • (6) An enhanced Δ for small semimajor axis & large eccentricity. Earlier table: Mercury (e = 0. 2056, a = 0. 3871 AU) should have the largest effect! Get: Mercury: Calc. : Δ 43. 03 /century. Obs. : Δ 43. 11 /century!