Aproximaciones y errores de redondeo Programacin numrica Cifras

Aproximaciones y errores de redondeo Programación numérica

Cifras significativas Las cifras significativas de un número son aquellas que pueden utilizarse en forma confiable. Se tratan del número de dígitos que se ofrecen con certeza más uno estimado. Los métodos numéricos dan resultados aproximados. Los números representados en las computadoras tienen un número finito de cifras significativas. A la omisión del resto de cifras significativas se le conoce como error de redondeo.

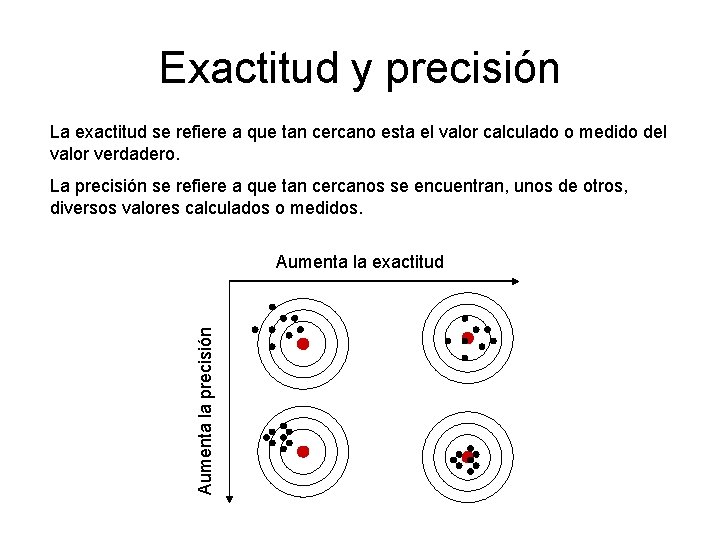
Exactitud y precisión La exactitud se refiere a que tan cercano esta el valor calculado o medido del valor verdadero. La precisión se refiere a que tan cercanos se encuentran, unos de otros, diversos valores calculados o medidos. Aumenta la precisión Aumenta la exactitud

Los métodos numéricos deben ser lo suficientemente exactos, o sin sesgo para satisfacer los requerimientos de un problema particular de ingeniería. También deben ser lo suficientemente precisos para ser adecuados en el diseño de ingeniería. En el curso usaremos el término error para representar tanto la inexactitud como la imprecisión en las predicciones.

Definición de error Los errores numéricos se pueden clasificar como Errores de truncamiento: resultan del empleo de aproximaciones con cálculos exactos. Errores de redondeo: por utilizar números que tienen un límite de cifras significativas. Error verdadero = Et = valor verdadero – valor aproximado Esta definición no toma en cuenta la magnitud de las cantidades involucradas. Error relativo fraccional verdadero = error verdadero / valor verdadero El error relativo porcentual verdadero se define como e t = error verdadero / valor verdadero x 100% El error aproximado se utiliza cuando no se conoce el valor verdadero. Se define por e a = error aproximado / valor aproximado x 100% El error en los métodos iterativos con las aproximaciones actual y anterior. e a = (aproximación actual – aproximación anterior) / aproximación actual x 100%

Ejemplo Se mide un puente y un remache, y se obtienen 9999 y 9 cm, respectivamente. Si los valores verdaderos son 10000 y 10 a) encontrar el error verdadero y b) el error relativo porcentual verdadero en cada caso. a) Puente: Et = 10000 – 9999 = 1 cm Remache: Et = 10 – 9 = 1 cm b) Puente: et = 1/10000 x 100% = 0. 01 % Remache: et = 1/10 x 100% = 10 %

Tarea a) Evalúe el polinomio y = x 3 – 7 x 2 + 8 x + 0. 35 En x = 1. 37, utilizando aritmética de 3 dígitos con truncamiento (corte). Evalúe el error relativo porcentual. b) Repita a) con y calculada con y = ((x – 7)x + 8)x + 0. 35 Evalúe el error y compárelo con el de a)

Tarea Escriba un programa en C que imprima una tabla con valores calculados de ex, para x = 0. 5 utilizando la expansión siguiente Imprima el número de términos (comenzando en 1), el resultado de la suma y el error relativo porcentual. Termine el proceso cuando el error relativo porcentual sea menor a 0. 004 %. El valor exacto determínelo con la función exp() de C.

/* Programa para evaluar la función exponencial en 0. 5 usando la serie de Taylor. */ #include <iostream> #include <math. h> int main(){ float x = 0. 5, suma = 1, pi = 3. 1415926535, error, fact = 1, pot = 1; int iter = 1; cout << "No. t. Sumat. Error" << “n”; do{ error = (suma-exp(x))/exp(x)*100. 0; std: : cout << iter << "t" << suma << "t" << error << "t" << “n”; pot *= x; //siguiente potencia de x fact *= iter; //siguiente factorial suma += pot/fact; //siguiente valor de la suma iter++; }while(fabs(error)>0. 004); system("PAUSE"); return 0; }

No. Suma Error 1 1 -39. 3469 2 1. 5 -9. 0204 3 1. 625 -1. 43877 4 1. 64583 -0. 17516 5 1. 64844 -0. 0172116 6 1. 6487 -0. 00141312 Presione una tecla para continuar. . .

Ejemplo La serie: Converge al valor f(n) = p 4/90, conforme n tiende a infinito. Escriba un programa de precisión sencilla para calcular para n =10000 por medio de calcular la suma desde i = 1 hasta 10000. Después repita el cálculo pero en sentido inverso, es decir, desde i = 10000 a 1, con incrementos de -1. En cada caso, calcule el error relativo porcentual verdadero. PI = 3. 141592653589793238

Error en el método de bisección Para el método de bisección se sabe que la raíz esta dentro del intervalo, la raíz debe situarse dentro de Dx / 2, donde Dx = xb – xa. La solución en este caso es igual al punto medio del intervalo xr = (xb + xa) / 2 Deberá expresarse por xr = (xb + xa) / 2 Dx / 2