Appunti di analisi matematica Integrale Definito Il concetto

Appunti di analisi matematica: Integrale Definito Il concetto d’integrale nasce per risolvere due classi di problemi: Integrale Indefinito Integrale Definito • Problema inverso del calcolo della derivata: nota la derivata di una funzione calcolare la funzione stessa. • Applicato ad esempio alle equazioni differenziali • Calcolo delle aree di fig. delimitate da curve • Calcolo di volumi • Calcolo del lavoro di una forza • Calcolo dello spazio percorso …. .

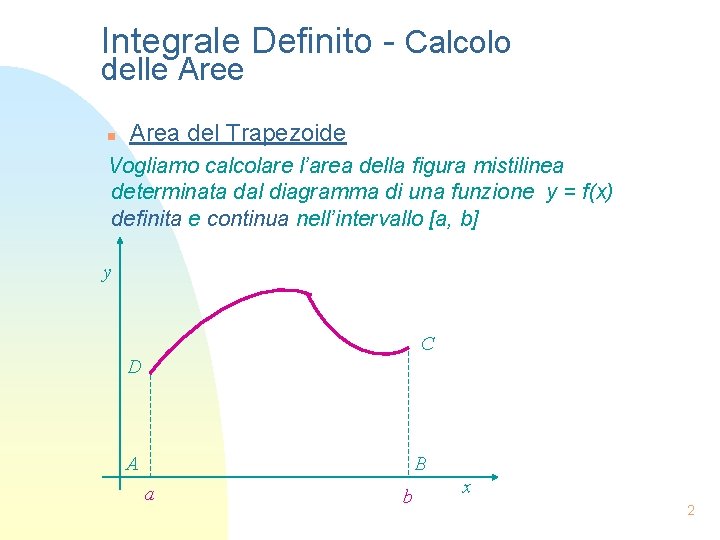
Integrale Definito - Calcolo delle Aree n Area del Trapezoide Vogliamo calcolare l’area della figura mistilinea determinata dal diagramma di una funzione y = f(x) definita e continua nell’intervallo [a, b] y C D A B a b x 2

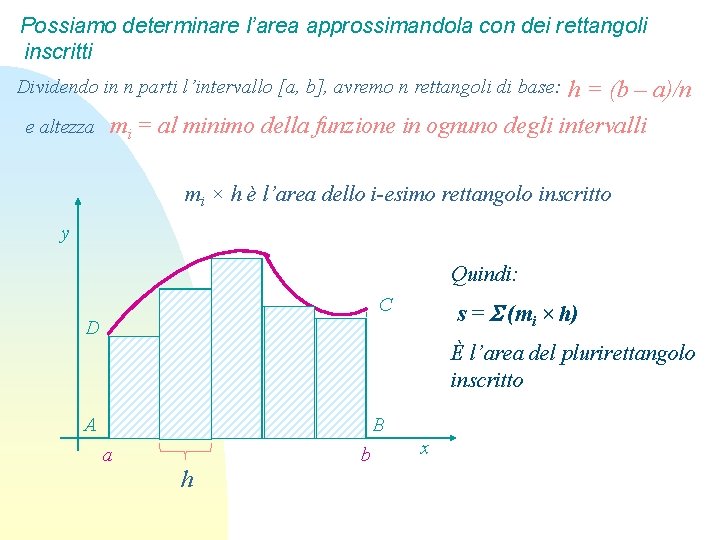
Possiamo determinare l’area approssimandola con dei rettangoli inscritti Dividendo in n parti l’intervallo [a, b], avremo n rettangoli di base: e altezza h = (b – a)/n mi = al minimo della funzione in ognuno degli intervalli mi × h è l’area dello i-esimo rettangolo inscritto y Quindi: C s = (mi × h) D È l’area del plurirettangolo inscritto mi A B a b h x

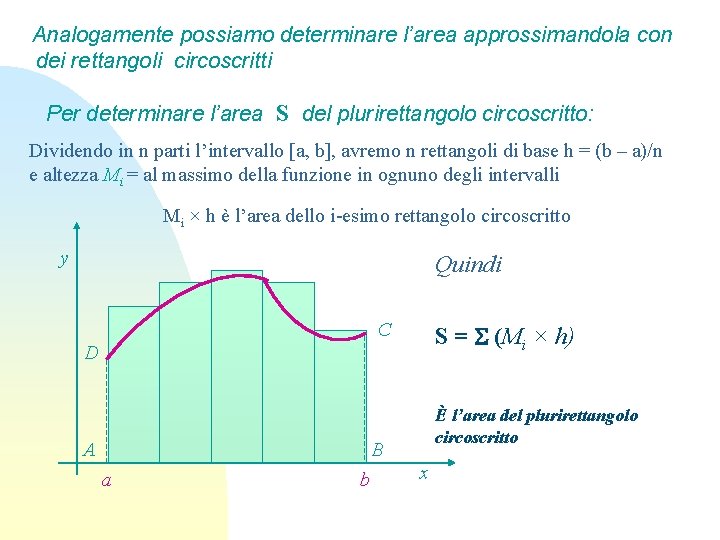
Analogamente possiamo determinare l’area approssimandola con dei rettangoli circoscritti Per determinare l’area S del plurirettangolo circoscritto: Dividendo in n parti l’intervallo [a, b], avremo n rettangoli di base h = (b – a)/n e altezza Mi = al massimo della funzione in ognuno degli intervalli Mi × h è l’area dello i-esimo rettangolo circoscritto y Quindi C S = (Mi × h) D A È l’area del plurirettangolo circoscritto B a b x

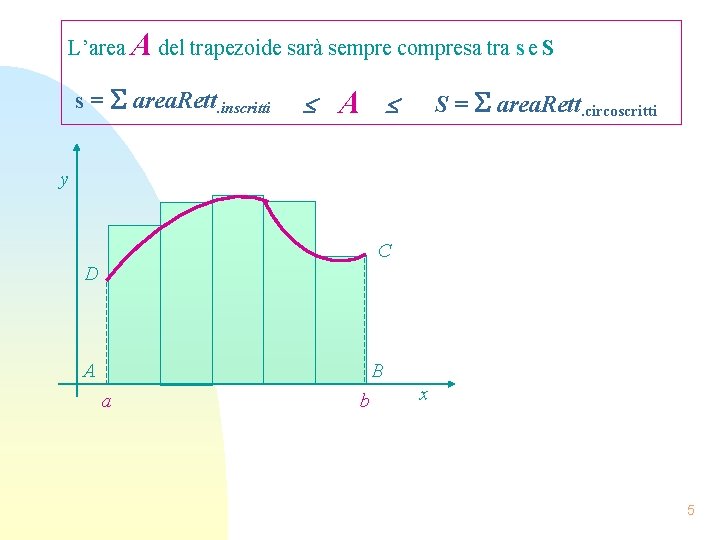
L’area A del trapezoide sarà sempre compresa tra s e S s = area. Rett. inscritti A S = area. Rett. circoscritti y C D A B a b x 5

Aumentando il numero dei rettangoli l’approssimazione di S sarà sempre più precisa. Considerando un numero di rettangolini via crescente avremo due successioni di aree: Ø plurirettangoli inscritti s 1, s 2, … sn, … Ø plurirettangoli circoscritti S 1, S 2, …Sn, … che convergono all’area del trapezoide ABCD Teorema. Se y = f(x) è continua e positiva in [a, b], allora le successioni delle aree s 1, s 2, … sn … e S 1, S 2, …Sn, … convergono allo stesso limite S uguale all’area del trapezoide ABCD

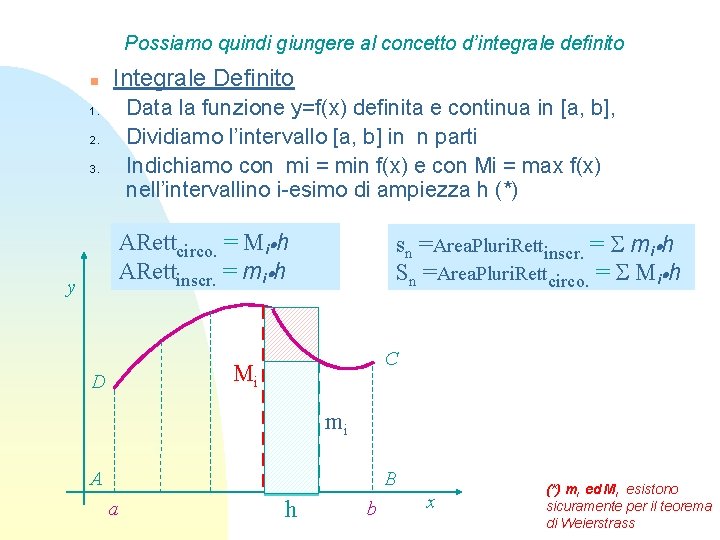
Possiamo quindi giungere al concetto d’integrale definito n Integrale Definito Data la funzione y=f(x) definita e continua in [a, b], Dividiamo l’intervallo [a, b] in n parti Indichiamo con mi = min f(x) e con Mi = max f(x) nell’intervallino i-esimo di ampiezza h (*) 1. 2. 3. ARettcirco. = Mi h ARettinscr. = mi h y sn =Area. Pluri. Rettinscr. = mi h Sn =Area. Pluri. Rettcirco. = Mi h C Mi D mi A a i h B b x (*) mi ed Mi esistono sicuramente per il teorema di Weierstrass

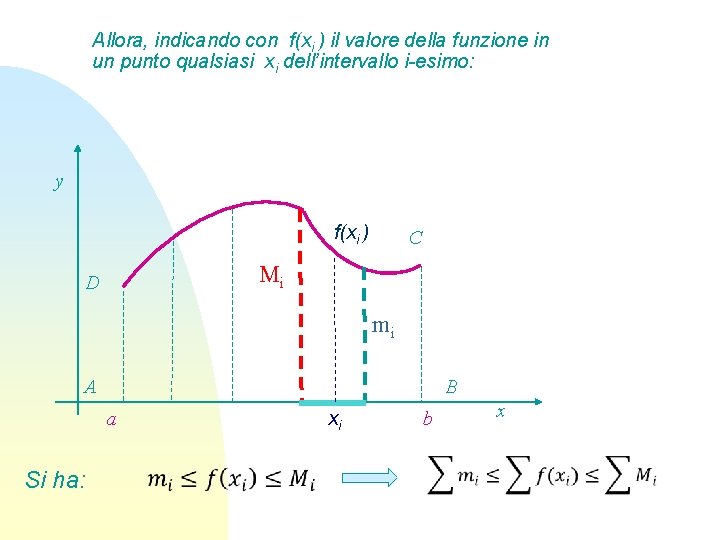
Allora, indicando con f(xi ) il valore della funzione in un punto qualsiasi xi dell’intervallo i-esimo: y f(xi ) C Mi D mi A B xi a Si ha: b x

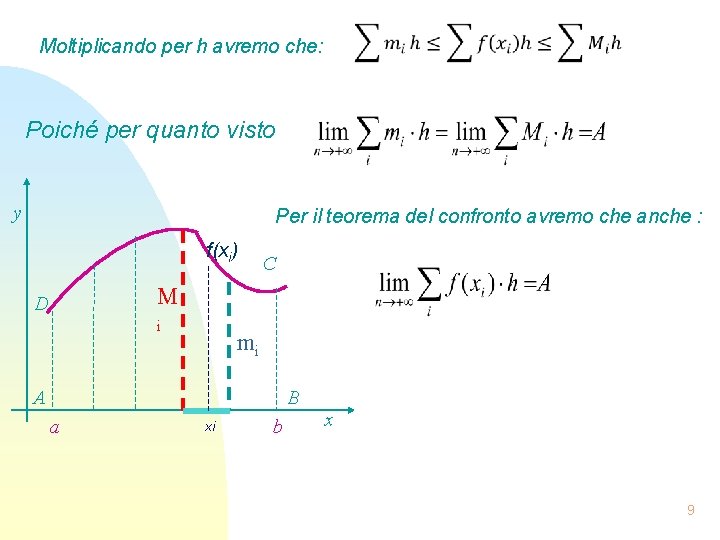
Moltiplicando per h avremo che: Poiché per quanto visto y Per il teorema del confronto avremo che anche : f(xi) C M D i mi A B a xi b x 9

Allora, possiamo dare la seguente definizione: Data la funzione y=f(x) continua in [a, b], si dice Integrale definito di f(x) relativo all’intervallo [a, b] il limite e si indica con

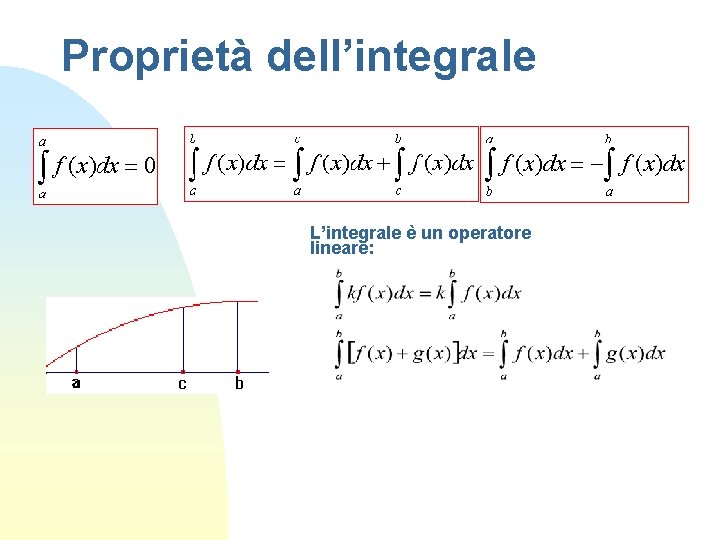
Proprietà dell’integrale L’integrale è un operatore lineare:

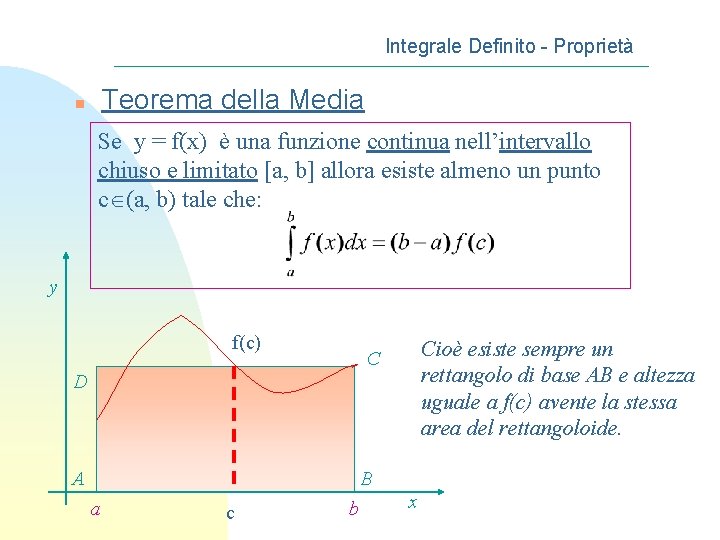
Integrale Definito - Proprietà Teorema della Media n Se y = f(x) è una funzione continua nell’intervallo chiuso e limitato [a, b] allora esiste almeno un punto c (a, b) tale che: y f(c) Cioè esiste sempre un rettangolo di base AB e altezza uguale a f(c) avente la stessa area del rettangoloide. C D A B a c b x

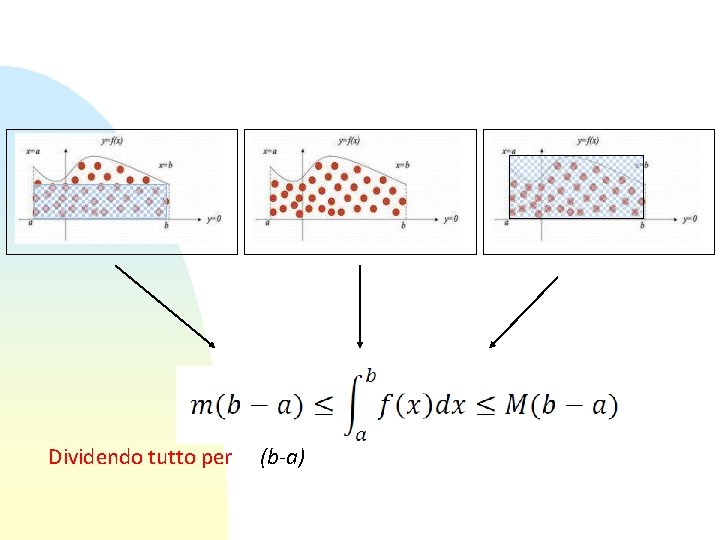
Dividendo tutto per (b-a)

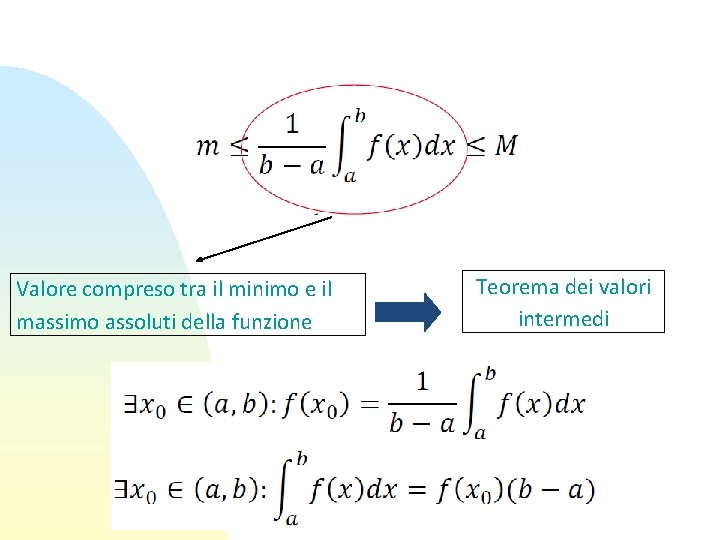
Valore compreso tra il minimo e il massimo assoluti della funzione Teorema dei valori intermedi

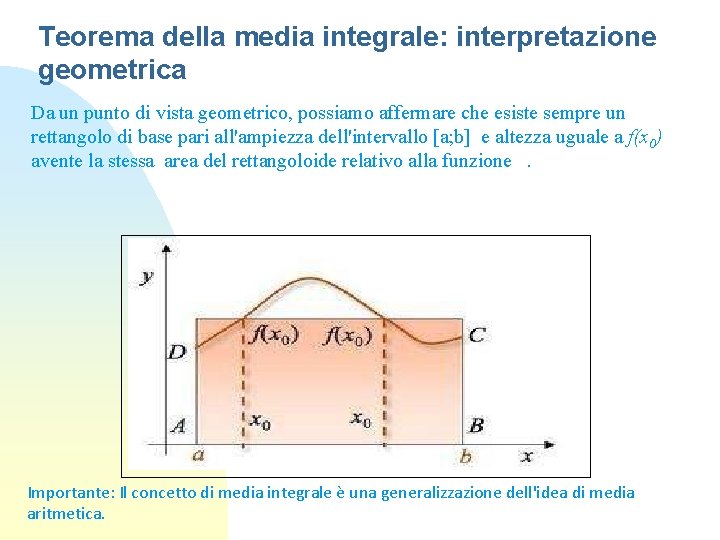
Teorema della media integrale: interpretazione geometrica Da un punto di vista geometrico, possiamo affermare che esiste sempre un rettangolo di base pari all'ampiezza dell'intervallo [a; b] e altezza uguale a f(x 0) avente la stessa area del rettangoloide relativo alla funzione . Importante: Il concetto di media integrale è una generalizzazione dell'idea di media aritmetica.

n Funzione Primitiva Il calcolo dell’integrale come limite delle somme indicate, ancorchè possibile può essere (e nella maggior parte dei casi lo è) estremamente complesso e per nulla conveniente, occorre allora trovare un altro sistema per calcolarlo. 16

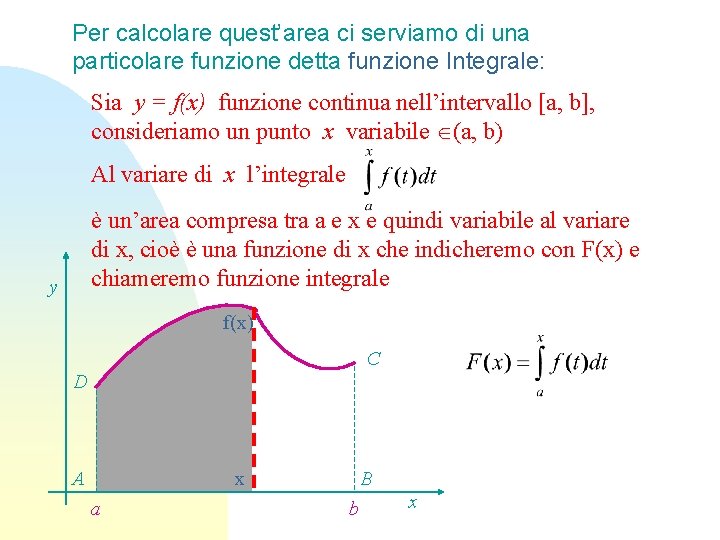
Per calcolare quest’area ci serviamo di una particolare funzione detta funzione Integrale: Sia y = f(x) funzione continua nell’intervallo [a, b], consideriamo un punto x variabile (a, b) Al variare di x l’integrale è un’area compresa tra a e x e quindi variabile al variare di x, cioè è una funzione di x che indicheremo con F(x) e chiameremo funzione integrale y f(x) C D A x a B b x

In particolare Se x = a se x = b La funzione integrale è caratterizzata dal seguente teorema fondamentale che ci fornirà il metodo per il calcolo dell’area: Teorema di Torricelli- Barrow Se y = f(x) è continua in [a, b] allora la funzione integrale è derivabile e risulta: F’(x) = f(x); cioè F(x) è una primitiva di f(x), cioè della funzione integrale calcolata nell’estremo superiore.

n Dim Consideriamo l’intervallino [x, x+h]: avremo y C D A B a x x + h b x L’incremento di F(x) (area del rettangoloide di base x, x+h) è:

semplificando Per il teorema della media esiste c nell’intervallo [x , x+h] tale che: Dividendo i termini per h: e, passando al limite per h 0,

Perché è proprio ? Non dimentichiamo che x < c < x+h per cui se h 0 c x Cioè la derivata di F(x) = f(x) 21

Ricordiamo che una funzione ammette infinite primitive che differiscono per una costante reale e costituiscono una famiglia di infinite curve ottenibili per traslazione secondo l’asse y. Se F(x) è una primitiva di f(x) allora anche G(x) = F(x) + c c R è una primitiva di f(x) e quindi se F(x) e G(x) sono primitive di f(x) allora: G(x) - F(x) = c 22

Integrale Definito - Proprietà n Calcolo dell’Integrale Definito Formula di Newton-Leibniz Finalmente possiamo calcolare l’integrale definito Considerando la funzione integrale avremo: e per x = a Da cui c = G(a) e per x = b

Integrale Definito - Proprietà n Teorema fondamentale del calcolo integrale L’integrale definito di una funzione continua y=f(x), calcolato nell’intervallo [a, b], è uguale alla differenza tra i valori che una qualunque primitiva di f(x) assume agli estremi superiore e inferiore dell’intervallo d’integrazione. 24