Approximations of points and polygonal chains Approximation of

Approximations of points and polygonal chains • Approximation of points by a line: find a line l (if one exists) such that all points are within distance ε from l, under some distance metric. • Other definitions possible: find line l that minimizes the maximum distance from the points to l.

Distance Metrics • Uniform metric (prev. slide). – yi-f(xi) ≤ ε • Euclidean metric. • L 1 and L∞ metrics. • Other measures possible (will be introduced latter).

Approx. of points by line • Each vertical line segment maps to a parallel strip in a dual point/line space (duality transform, to be explained shortly). • Can define the strip as intersection of two halfplanes. • Then solve a 2 -D linear programming (LP) problem, which takes O(n) time.

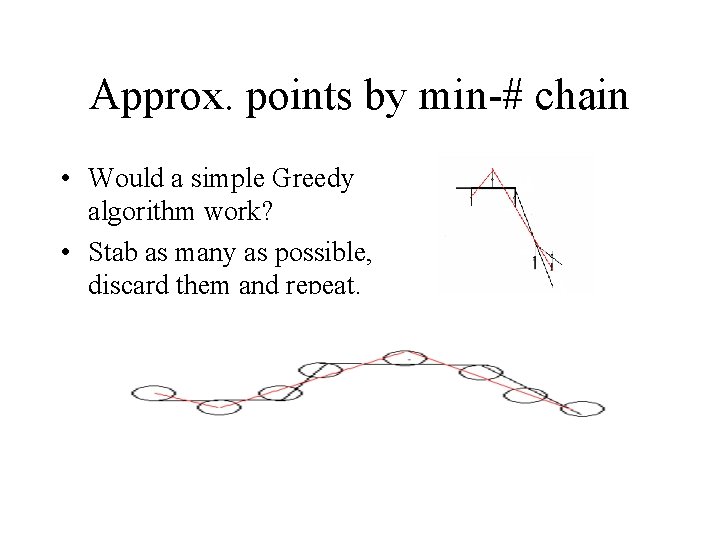
Approx. points by min-# chain • Would a simple Greedy algorithm work? • Stab as many as possible, discard them and repeat.

Greedy vs. Dynamic Programming • If objects are convex and disjoint, O(n) time greedy algorithm is possible (vertices are unrestricted, that is, can lie anywhere). • For intersecting objects, dynamic programming gives O(n 2) and O(n 2 log n) time, depending on how visiting order of objects is defined.

Min-# vs. Min-ε • Min-#: given some error bound, minimize number of vertices of approximating path. • Min-ε: minimize the error of an approximating path that has at most a specified number of vertices, m (m < n). – If finite set of possible approximation errors, and if set can be computed in reasonable time, then can use min-# to solve min-ε.

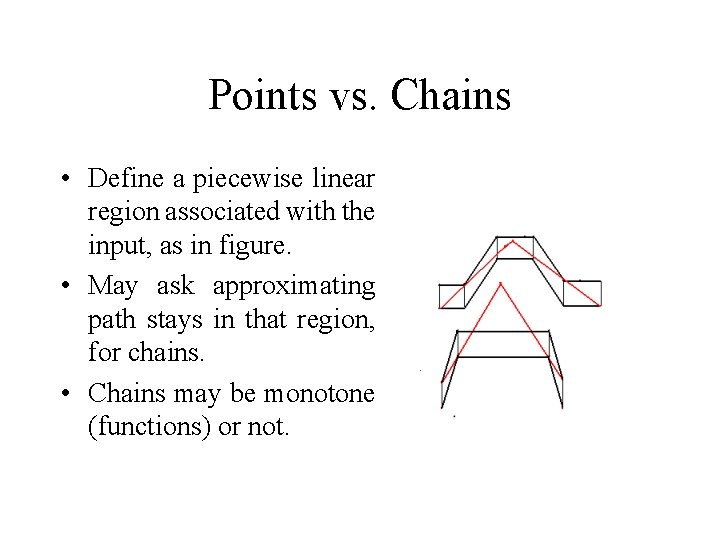
Points vs. Chains • Define a piecewise linear region associated with the input, as in figure. • May ask approximating path stays in that region, for chains. • Chains may be monotone (functions) or not.

Min-# for Piecewise Linear Function • Approximation must stay in error region. • Approximation sought: monotone polygonal line with min-# of vertices. • Use “edge visibility” concept. – A point u of polygon P is visible from edge e, if there is point v on e such that line segment uv is contained in P. – An edge e’ is visible from e if there is a point of e’ visible from e. – Visibility polygon VP(P, e): points of P visible from e.

Visibility: VP(P, e) • VP(P, e) splits the polygon in a few connected regions: – Visible region/polygon; – Invisible polygons. • Consider the invisible polygon P’ that contains end point of chain. – Common boundary of P and P’ is a line segment called “window”. • Use “convex hull” algorithm to find windows. • Results in O(n) time algorithm.

Error criteria for chains • E 1: Tolerance zone. • E 2: Parallel-strip (also called “infinite beam”). • E 3: Parallel rectangle: half of min. width of rectangle containing pk, i≤ k≤ j, with parallel sides orthogonal on line segment pipj. • E 4: Rectangle: required only contain pk, i≤ k ≤j.

General Approach Using Graphs • Given: C=p 1 p 2…pn, polygonal chain. • Directed graph G(C): – Vertex vi corresponds to point pi. – Edge (vi, vj) has weight = error of segment pipj. • For given error bound ε: G(C, ε): – Subgraph of G with edge weights ≤ ε. – A path in G(C, ε): corresponds to approximating curve with error at most ε. • Approximating curve for min-#: – Shortest path from v 1 to vn in G(C, ε) (length is # arcs). – Use BFS to find it. • Min-ε: minimize ε such that in G(C, ε) there is path with at most a specified # of vertices.

Complexity • If G(C) can be computed in f(n) time: – Min-# can be solved in O(f(n)+n 2) time. – Min-ε can be solved in O(f(n)+n 2 log n) time. • If G(C, ε) can be computed in g(n) time: – Min-# can be solved in O(g(n)+n 2) time. • Most of known solutions use this approach (see solution on handout paper for some exceptions). • The “closed” min-# and min-ε problems can eventually be solved by solving n “open” problems (better in some cases; depends on restrictions).

Complexities • Under error criteria discussed: – e 1: O(n 2) and O(n 2 log n) time, O(n) space. • Constructs G(C, ε). • Makes use of binary search with less space. – e 2: O(n 2 log n) time, O(n) and O(n 2) space. • Constructs G(C). • O(n 2) possible if some condition holds. • Even o(n 2) possible if that condition holds. – e 3: O(n 2 log n) time, O(n 2) space (O(n) space possible? !). • Constructs G(C). – e 4: O(n log n) time, O(mn log (n/m)) space.

Min-# under E 4 • • Property: In G(C, ε), if (vi, vj) є G, then (vk, vl) є G, i ≤ k < l ≤ j. Algorithm 1: 1. v=1; i(1)=1; 2. i(v+1)=max{j | (vi, vj) є G(c, ε)}; 3. if i(v+1)==n then done; else v=v+1; return to 2. • The algorithm is greedy.

E 4 (cont. ) • There is a rectangle of width w that covers a set V of points such that it contains an edge of CH(V). • W(i, j): min. width of rectangle covering V. • For e є CH(V): – Antipodal point: point v of CH(V) farthest from line containing e. – d(e): distance from v to line containing e. • W(i, j)=min{d(e) | e is on CH(i, j)}. • Given CH(V), can find antipodal points of all edges in O(|V|) time.

E 4 (cont. ) • Algorithm 1’: 1. v=1; i(1)=1; 2. i(v+1)=max{j | i(v) < j ≤ n, W(i(v), j) ≤ w}; 3. if i(v+1)==n then done; else v=v+1; go to step 2. • Step 2 is main step. • Will show for v=1 van be executed in O(i* log i*) where i*=i(2).

E 4 (cont. ) • W(1, j) nondecreasing in j: use doubling binary search to find i*. • Find m, l such that W(1, m) ≤ w, W(1, l) > w and m < l ≤ min{2 m, n} – Start with m=1, l=2; double each until holds. • i* lies between m and l-1. • Again binary search to find i*:

E 4 (cont. ) • Algorithm 2: 1. k=m; l=l-1; Construct and keep CH(1, k); 2. h=(k+l)/2; Construct CH(k+1, h); Construct CH(1, h) from CH(1, k), CH(k+1, h); Compute wh=W(1, h); 3. If wh ≤ w then k=h; else l=h-1; If k==l then i*=k and done; else keep CH(1, k) and go to step 2.

E 4 (cont. ) • • Algorithm 1’+2 takes O(n log n). Compute W(1, 2 g), g=1, 2, . . , M+1, M=log m. W(1, j) can be found in O(j log j). O(Σ 2 glog 2 g)=O(i*logi*). – Note that m=O(i*). • Step 2 in Alg. 2 takes O(i*logi*) – CH(1, h): O(h) (from CH(1, k) and CH(k+1, h); – W(1, h): O(h) time; – In g-th iteration CH(k+1, h) is on at most m 2 -g=2 M-g points: O(2 M-glog 2 M-g) time. • Executed at most M times (g=1, …M): O(Σ 2 M-glog. M-g)=O(i*logi*).

Min-ε under E 4 • • O(mn(log n)(log n/m) time. (output sensitive). Algorithm 3 (compute min. width w*). 1. 2. M’=m; i=1; w=0; Find j, by doubling binary search, such that 1. 2. 3. 1. i < j ≤ n, pi, …, pn cannot be covered by m’ or fewer rectangles with width less than W(i, j), pi, …, pn can be covered by m’ or fewer rectangles with width less than W(i, j+1). i=j; m’=m-1; w=max{w, W(i, j)}; If i=n done; else go to step 2. Note: in a sequence of rectangles with width w* found by min-#, the first rectangle cover points p 1, …, pj, where j is found in first execution of step 2 above (then induction).