Approximation of Functions Approximation problems divided into five

Approximation of Functions Approximation problems divided into five parts: ü Least square approximation of discrete functions or Regression ü Least square approximation of continuous function using various basis polynomials ü Orthogonal basis functions ü Approximation of periodic functions ü Interpolation

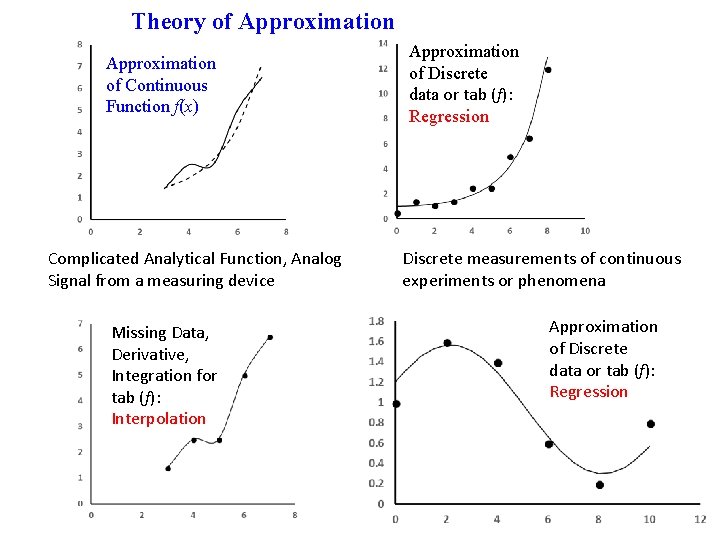
Theory of Approximation of Continuous Function f(x) Complicated Analytical Function, Analog Signal from a measuring device Missing Data, Derivative, Integration for tab (f): Interpolation Approximation of Discrete data or tab (f): Regression Discrete measurements of continuous experiments or phenomena Approximation of Discrete data or tab (f): Regression

Approximation of Functions •

Approximation of Functions When not to use polynomial basis? ü If the functional form or the model is known ü Sharp front ü Periodic function

Function Space vs. Vector Space •

Norm and Seminorm •

Inner Product •

Basis Functions: Linear Independence •

Orthogonal Functions •

Least Square Problem •

Schematic of Least Square Solution f(x)

Least Square Solution: Proof •

Least Square Solution: Proof •

Least Square Solution: Normal Equations •

Least Square Solution: Normal Equations •

Least Square Solution: Existence and Uniqueness •

Least Square Solution: Existence and Uniqueness •

Least Square Solution: Example (Continuous) •

Least Square Solution: Example (Continuous) •