Approximation and Idealization Why the Difference Matters John

Approximation and Idealization Why the Difference Matters John D. Norton Department of History and Philosophy of Science Center for Philosophy of Science University of Pittsburgh Rotman Institute of Philosophy March 15, 2013 1

This Talk 1 Stipulate that: “Approximations” are inexact descriptions of a target system. “Idealizations” are novel systems whose properties provide inexact descriptions of a target system. 3 2 Infinite limit systems can have quite unexpected behaviors and fail to provide idealizations. Extended example: Thermodynamic and other limits of statistical mechanics. Infinite idealizations are often only limiting property approximations. Fruitless debates over reduction and reduction emergence in phase transitions derive from unnoticed differences in the notion of level. emergence theory scale 2

Characterizing Approximation and Idealization 3

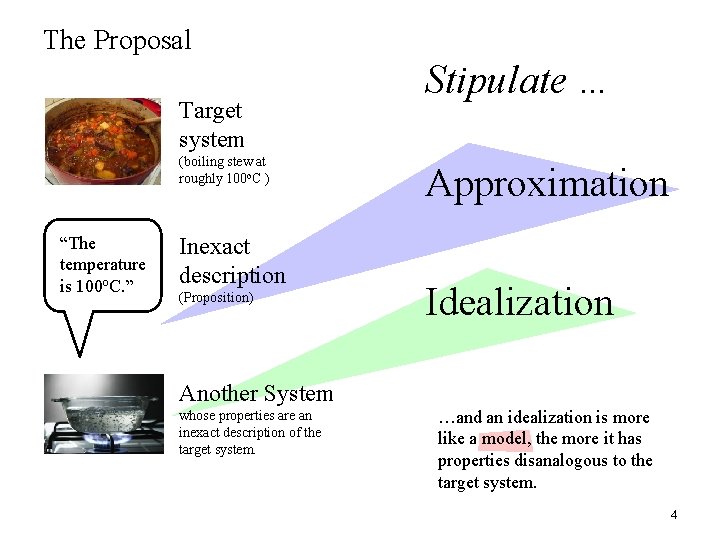
The Proposal Target system (boiling stew at roughly 100 o. C ) “The temperature is 100 o. C. ” Inexact description (Proposition) Stipulate … Approximation Idealization Another System whose properties are an inexact description of the target system. …and an idealization is more like a model, the more it has properties disanalogous to the target system. 4

A Well-Behaved Idealization Target: Body in free fall dv/dt = g – kv v(t) = (g/k)(1 – exp(-kt)) = gt - gkt 2/2 + gk 2 t 3/6 - … Body in free fall in a vacuum v = gt Exact description v = gt Idealization for Inexact description for the first moments of fall (t is small). first moments of fall. Approximation 5

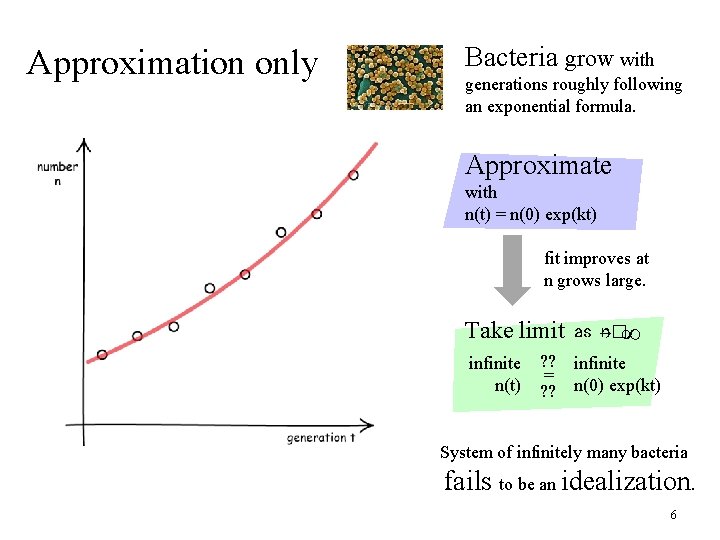
Approximation only Bacteria grow with generations roughly following an exponential formula. Approximate with n(t) = n(0) exp(kt) fit improves at n grows large. Take limit infinite n(t) ? ? = ? ? as n�∞ infinite n(0) exp(kt) System of infinitely many bacteria fails to be an idealization. 6

Using infinite Limits to form idealizations 7

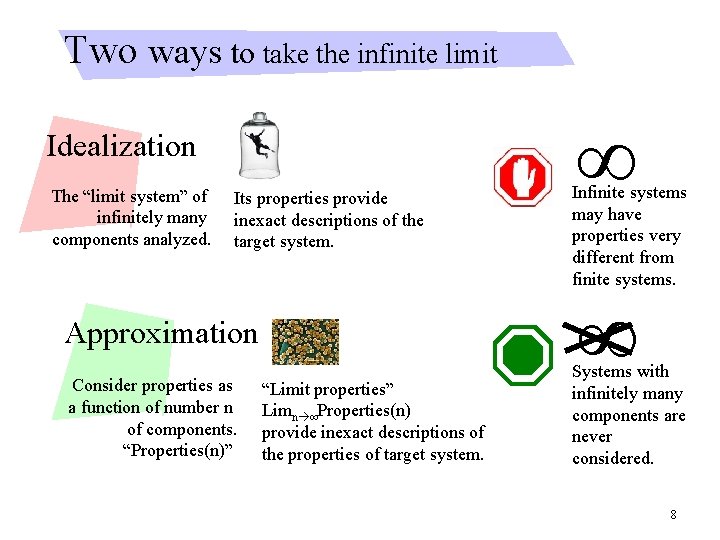
Two ways to take the infinite limit Idealization The “limit system” of infinitely many components analyzed. Its properties provide inexact descriptions of the target system. Approximation Consider properties as a function of number n of components. “Properties(n)” “Limit properties” Limn ∞Properties(n) provide inexact descriptions of the properties of target system. ∞ Infinite systems may have properties very different from finite systems. ∞ Systems with infinitely many components are never considered. 8

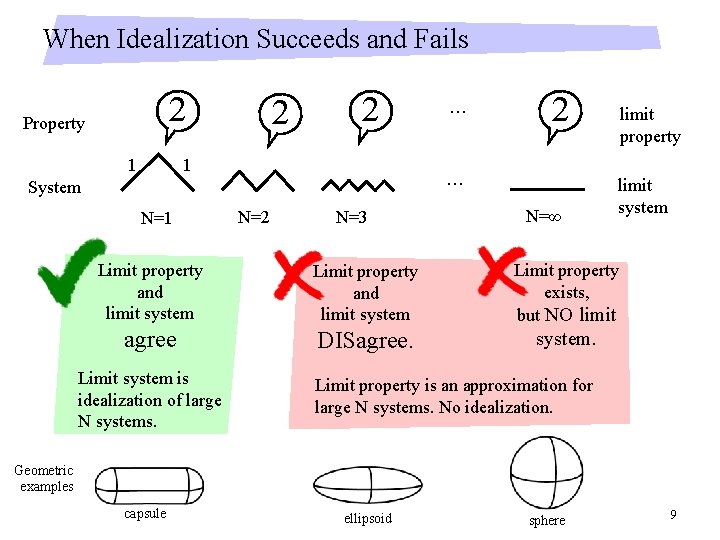
When Idealization Succeeds and Fails 2 Property 1 2 2 1 2 … System N=1 … N=2 N=3 N=∞ limit property limit system Limit property and limit system agree Limit property exists, but NO limit DISagree. system. Limit system is idealization of large N systems. Limit property is an approximation for large N systems. No idealization. Geometric examples capsule ellipsoid sphere 9

Continuum limit as an approximation 10

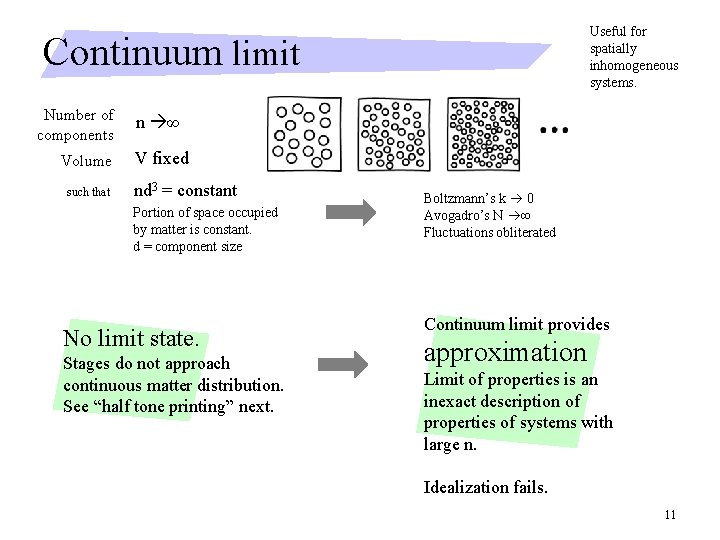
Useful for spatially inhomogeneous systems. Continuum limit Number of components Volume such that n ∞ V fixed nd 3 = constant Portion of space occupied by matter is constant. d = component size No limit state. Stages do not approach continuous matter distribution. See “half tone printing” next. Boltzmann’s k 0 Avogadro’s N ∞ Fluctuations obliterated Continuum limit provides approximation Limit of properties is an inexact description of properties of systems with large n. Idealization fails. 11

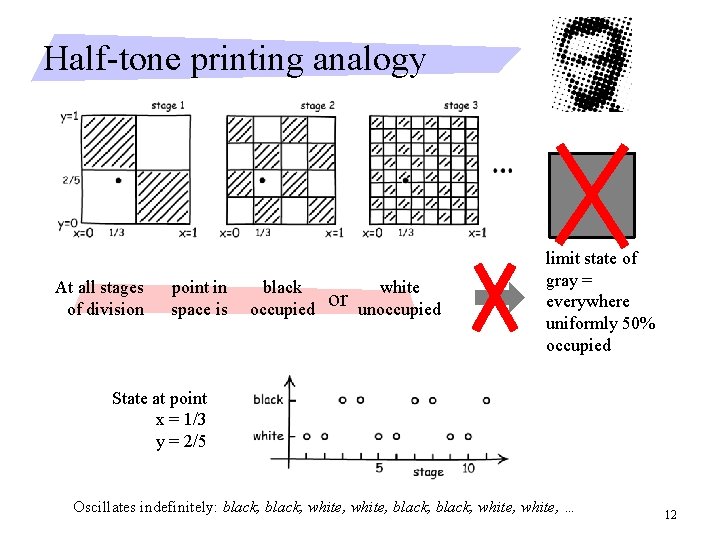
Half-tone printing analogy At all stages of division point in space is black occupied or white unoccupied limit state of gray = everywhere uniformly 50% occupied State at point x = 1/3 y = 2/5 Oscillates indefinitely: black, white, … 12

Thermodynamic limit as an idealization 13

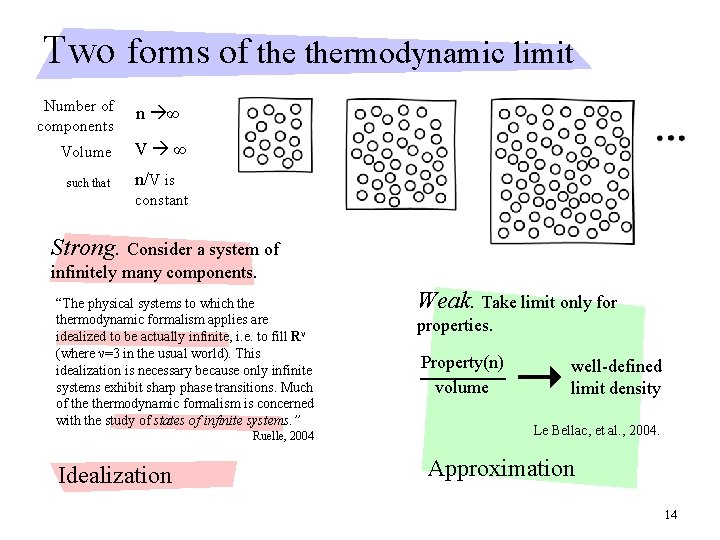
Two forms of thermodynamic limit Number of components Volume such that n ∞ V ∞ n/V is constant Strong. Consider a system of infinitely many components. “The physical systems to which thermodynamic formalism applies are idealized to be actually infinite, i. e. to fill Rν (where ν=3 in the usual world). This idealization is necessary because only infinite systems exhibit sharp phase transitions. Much of thermodynamic formalism is concerned with the study of states of infinite systems. ” Ruelle, 2004 Idealization Weak. Take limit only for properties. Property(n) volume well-defined limit density Le Bellac, et al. , 2004. Approximation 14

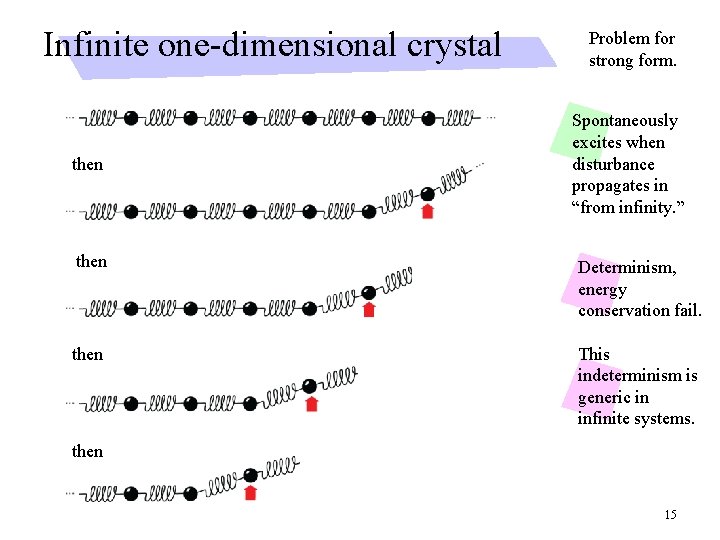
Infinite one-dimensional crystal then Problem for strong form. Spontaneously excites when disturbance propagates in “from infinity. ” then Determinism, energy conservation fail. then This indeterminism is generic in infinite systems. then 15

Strong Form: Must Prove Determinism Simplest one dimensional system of interacting particles. Clause bars monsters not arising in finite case. 16

Inessential complications…? ? “We emphasize that we are not considering theory of infinite systems for its own sake so much as for the fact that this is the only precise way of removing inessential complications due to boundary effects, etc. , …” But now extra conditions have to be added by hand to reproduce the essential functions of the boundary conditions. Lanford, 1975, p. 17 Another case: Boltzmann-Grad limit. Limit system and limit properties disagree. Limit system becomes indeterministic. Molecular collisions can no longer be resolved uniquely. 17

Renormalization Group Methods 18

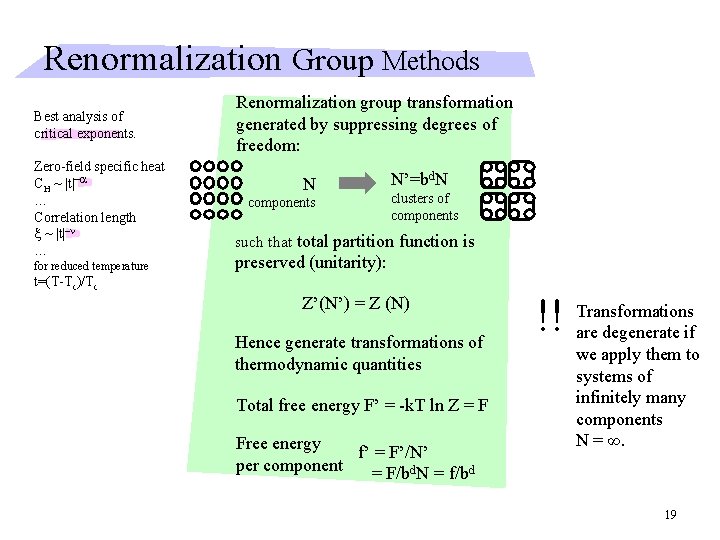
Renormalization Group Methods Best analysis of critical exponents. Zero-field specific heat CH ~ |t|-a … Correlation length x ~ |t|-n … for reduced temperature Renormalization group transformation generated by suppressing degrees of freedom: N components N’=bd. N clusters of components such that total partition function is preserved (unitarity): t=(T-Tc)/Tc Z’(N’) = Z (N) Hence generate transformations of thermodynamic quantities Total free energy F’ = -k. T ln Z = F Free energy f’ = F’/N’ per component = F/bd. N = f/bd !! Transformations are degenerate if we apply them to systems of infinitely many components N = ∞. 19

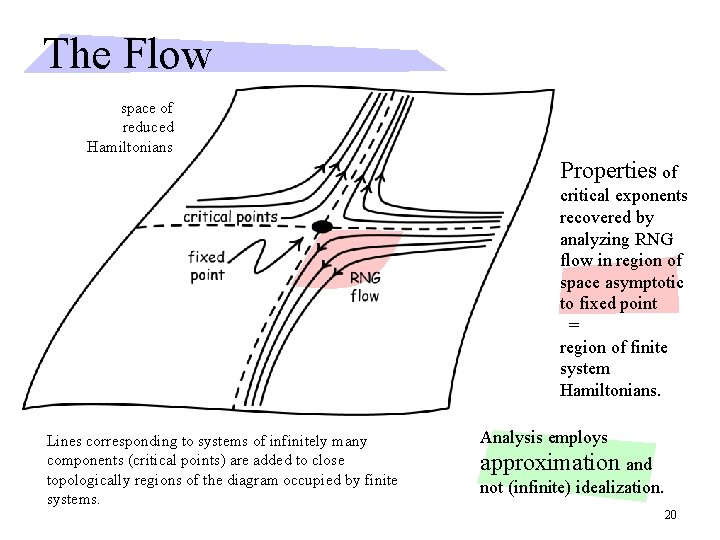
The Flow space of reduced Hamiltonians Properties of critical exponents recovered by analyzing RNG flow in region of space asymptotic to fixed point = region of finite system Hamiltonians. Lines corresponding to systems of infinitely many components (critical points) are added to close topologically regions of the diagram occupied by finite systems. Analysis employs approximation and not (infinite) idealization. 20

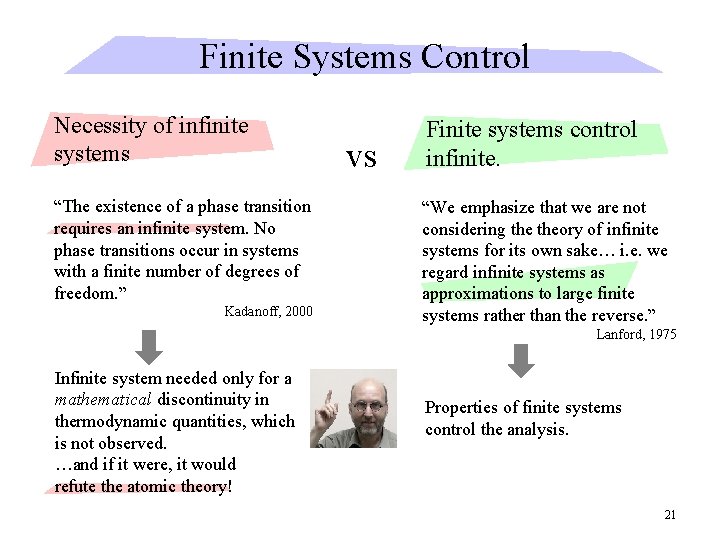
Finite Systems Control Necessity of infinite systems “The existence of a phase transition requires an infinite system. No phase transitions occur in systems with a finite number of degrees of freedom. ” Kadanoff, 2000 vs Finite systems control infinite. “We emphasize that we are not considering theory of infinite systems for its own sake… i. e. we regard infinite systems as approximations to large finite systems rather than the reverse. ” Lanford, 1975 Infinite system needed only for a mathematical discontinuity in thermodynamic quantities, which is not observed. …and if it were, it would refute the atomic theory! Properties of finite systems control the analysis. 21

Reduction? Emergence? 22

Phase transitions are… Norton, Butterfield … a success of the reduction of thermodynamics by statistical mechanics. … a clear example of non-reductive emergence. Who is right? BOTH!. . and no one is more right. 23

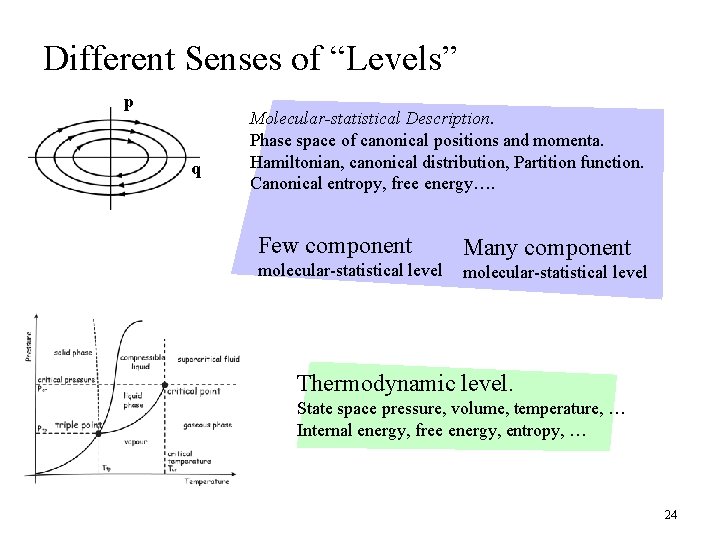
Different Senses of “Levels” p q Molecular-statistical Description. Phase space of canonical positions and momenta. Hamiltonian, canonical distribution, Partition function. Canonical entropy, free energy…. Few component molecular-statistical level Many component molecular-statistical level Thermodynamic level. State space pressure, volume, temperature, … Internal energy, free energy, entropy, … 24

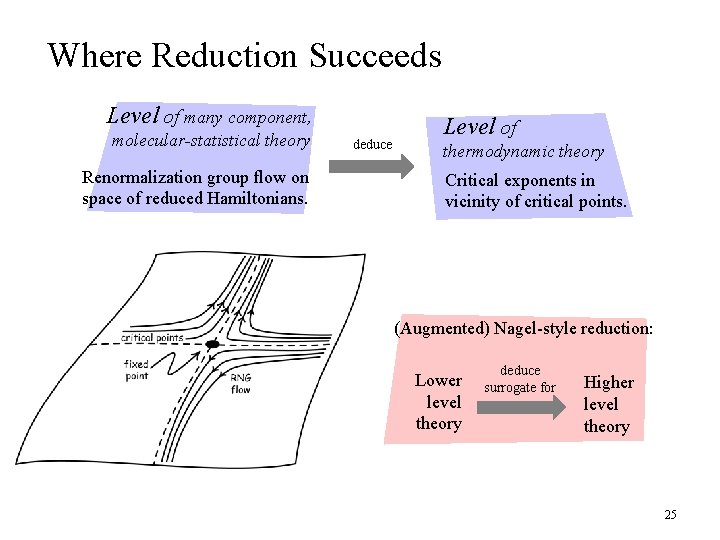
Where Reduction Succeeds Level of many component, molecular-statistical theory Renormalization group flow on space of reduced Hamiltonians. deduce Level of thermodynamic theory Critical exponents in vicinity of critical points. (Augmented) Nagel-style reduction: Lower level theory deduce surrogate for Higher level theory 25

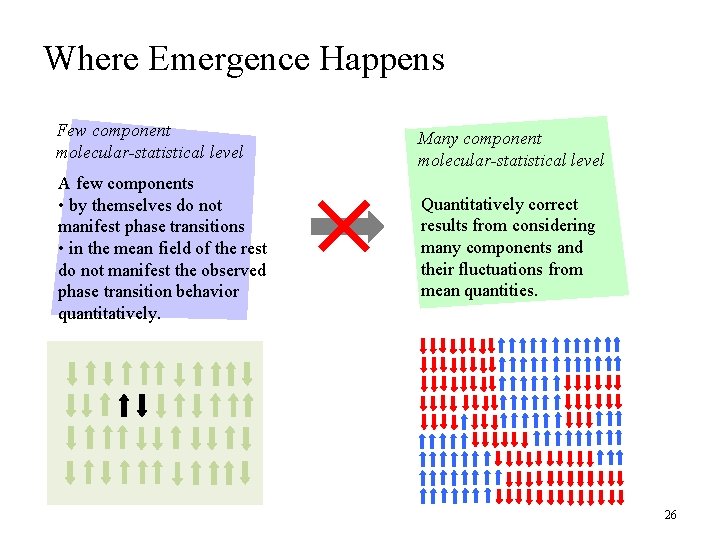
Where Emergence Happens Few component molecular-statistical level Many component molecular-statistical level A few components • by themselves do not manifest phase transitions • in the mean field of the rest do not manifest the observed phase transition behavior quantitatively. Quantitatively correct results from considering many components and their fluctuations from mean quantities. 26

“More is Different…” P. W. Anderson, Science, 1972. "The constructionist hypothesis [ability to start from fundamental laws and reconstruct the universe] breaks down when confronted with the twin difficulties of scale and complexity. The behavior of large and complex aggregates of elementary particles, it turns out, is not to be understood in terms of a simple extrapolation of the properties of a few particles. Instead, at each level of complexity, entirely new properties appear. . . ” few atoms--symmetry N H H H invert H H H many atoms—broken symmetry N Leo Kadanoff "More is the Same…. " Journal of Statistical Physics, 137 (December 2009) do not invert Phase transitions are “a prime example of Anderson’s thesis. ” 27

A conjecture… Philosophers tend to divide by theory. … but n ot philosop he suspicio rs us o theories f as units. Theory = deductive closure of a few apt propositions. Physicists tend to divide by scale. Condensed matter physics deals with systems of many components. Solids, liquids, condensates, … Level = theory Level = processes at same scale Reduction/emergence between selfcontained theories of thermodynamic and statistical mechanics. Reduction/emergence between systems of few components and many components. Cannot mix results from different theories in one level. (deductive closure) Draw whichever results needed from any applicable theory. Few-many distinction is within one theory. Mean field theory is an Few-many distinction divides condensed matter physics from atomic and particle physics. approximation, not a level. 28

Conclusion 29

This Talk 1 Stipulate that: “Approximations” are inexact descriptions of a target system. “Idealizations” are novel systems whose properties provide inexact descriptions of a target system. 3 2 Infinite limit systems can have quite unexpected behaviors and fail to provide idealizations. Extended example: Thermodynamic and other limits of statistical mechanics. Infinite idealizations are often only limiting property approximations. Fruitless debates over reduction and reduction emergence in phase transitions derive from unnoticed differences in the notion of level. emergence theory scale 30

Read 31

http: //www. pitt. edu/~jdnorton 32

33

34

35

The End 36

Commercial 37

38

39

Appendices 40

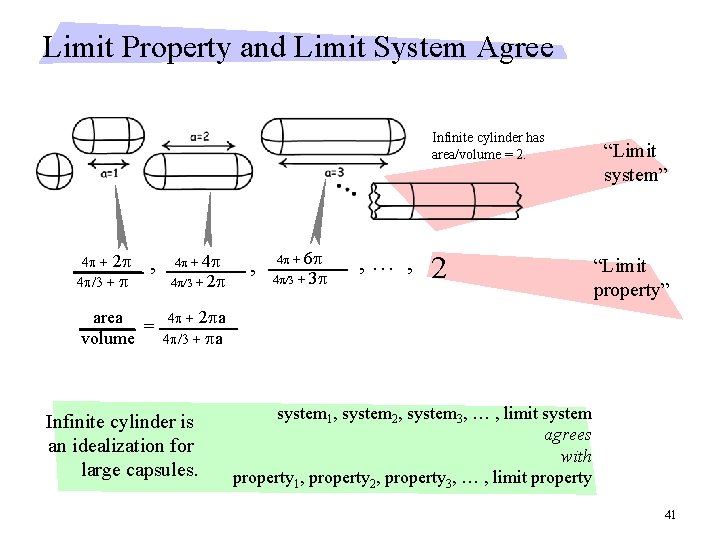
Limit Property and Limit System Agree Infinite cylinder has area/volume = 2. , 4 p 4 p/3 + 2 p area = volume 4 p + 2 pa 4 p/3 + pa 4 p + 2 p 4 p/3 + p 4 p + Infinite cylinder is an idealization for large capsules. , 6 p 4 p/3 + 3 p 4 p + , … , 2 “Limit system” “Limit property” system 1, system 2, system 3, … , limit system agrees with property 1, property 2, property 3, … , limit property 41

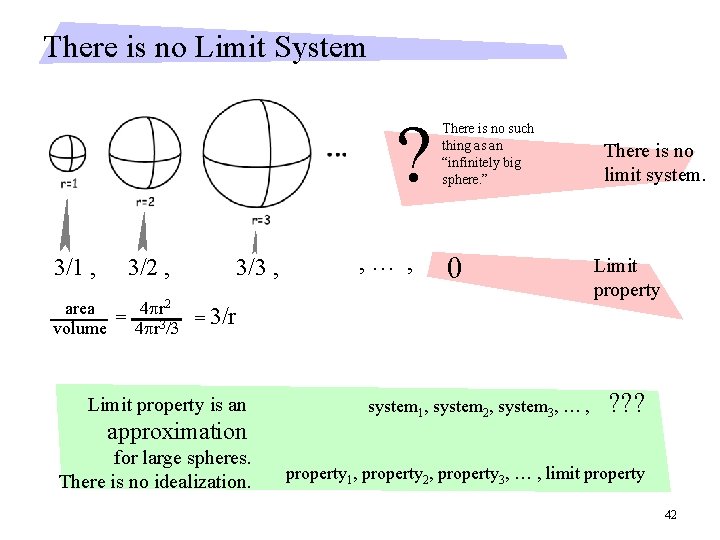
There is no Limit System ? 3/1 , 3/2 , 3/3 , , … , There is no such thing as an “infinitely big sphere. ” 0 area = 4 pr 2 = 3/r volume 4 pr 3/3 Limit property is an approximation for large spheres. There is no idealization. system 1, system 2, system 3, … , There is no limit system. Limit property ? ? ? property 1, property 2, property 3, … , limit property 42

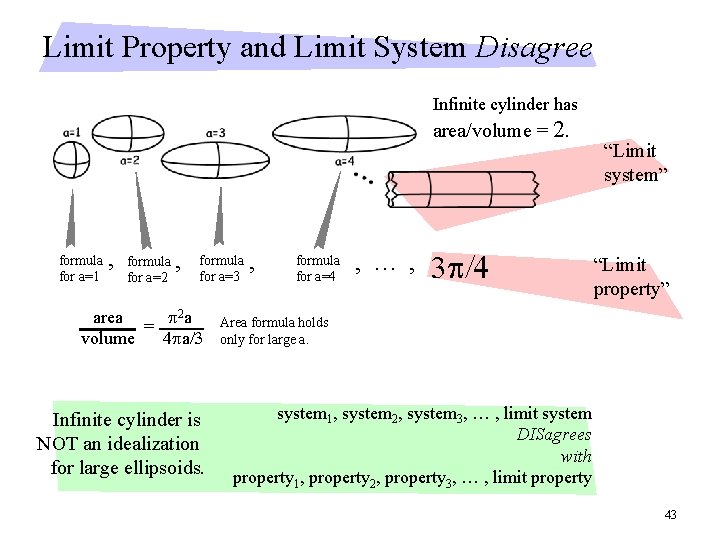
Limit Property and Limit System Disagree Infinite cylinder has area/volume = 2. formula for a=1 , formula for a=2 , formula for a=3 area = p 2 a volume 4 pa/3 Infinite cylinder is NOT an idealization for large ellipsoids. , formula for a=4 , … , 3 p/4 “Limit system” “Limit property” Area formula holds only for large a. system 1, system 2, system 3, … , limit system DISagrees with property 1, property 2, property 3, … , limit property 43

Limits in Statistical Physics 44

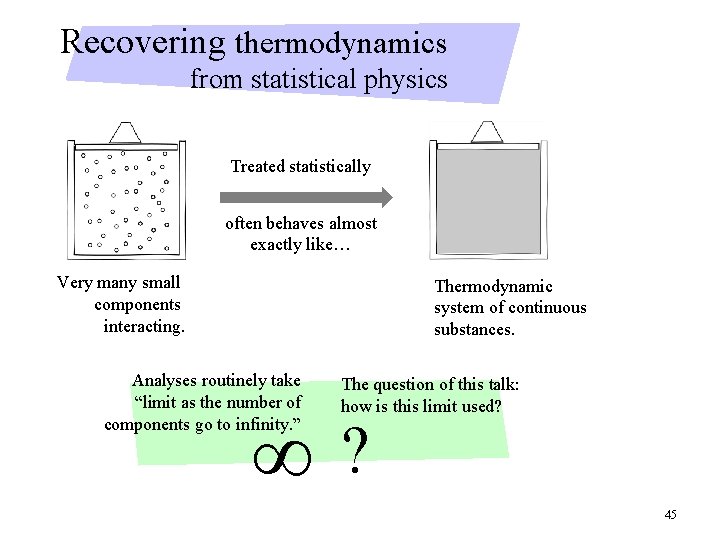
Recovering thermodynamics from statistical physics Treated statistically often behaves almost exactly like… Very many small components interacting. Thermodynamic system of continuous substances. Analyses routinely take “limit as the number of components go to infinity. ” ∞ The question of this talk: how is this limit used? ? 45

Boltzmann-Grad limit as an approximation 46

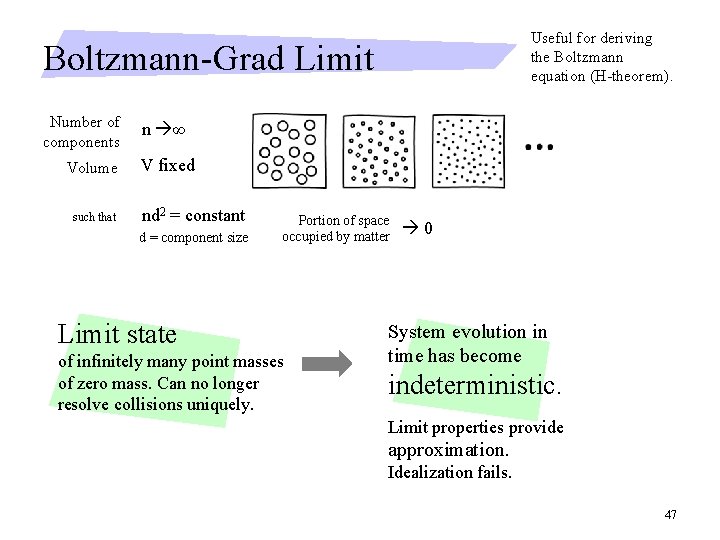
Useful for deriving the Boltzmann equation (H-theorem). Boltzmann-Grad Limit Number of components Volume such that n ∞ V fixed nd 2 = constant d = component size Portion of space occupied by matter Limit state of infinitely many point masses of zero mass. Can no longer resolve collisions uniquely. 0 System evolution in time has become indeterministic. Limit properties provide approximation. Idealization fails. 47

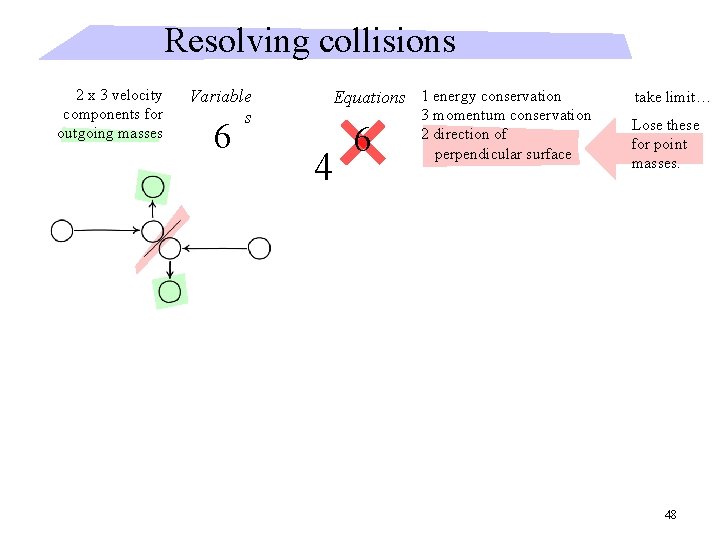
Resolving collisions 2 x 3 velocity components for outgoing masses Variable s 6 Equations 1 energy conservation 4 6 3 momentum conservation 2 direction of perpendicular surface take limit… Lose these for point masses. 48