Approximation Algorithms Introduction In general computer cannot solve

Approximation Algorithms Introduction • In general, computer cannot solve NPC problem efficiently • But, many NPC problems are too important to abandon • If a problem is an NPC problem, you may try to – find a pseudo polynomial time algorithm if it is not NPC in the strong sense – solve restricted problems – find approximation algorithms (also known as heuristics; usually a simple & fast algorithm) Young CS 530 Ad. Algo. D&A Approximation Algorithms 1

• Let’s consider optimization problems only • An algorithm A is an approximation for a problem L : if given any valid instance I, it finds a solution A(I) for L and A(I) is “close” to optimal solution OPT(I). [sometime, it will be nice to also include - If I is an invalid instance (with no solution) then it should return “no solution”]. Young CS 530 Ad. Algo. D&A Approximation Algorithms 2

• Approximation ration (or bound) of approximation algorithm A for problem L A(I)/OPT(I) ; if L is a minimization problem and A(I) OPT(I) > 0 OPT(I)/A(I) ; if L is a maximization problem and OPT(I) A(I) > 0 • When you provide an algorithm (pseudopolynomial/heuristic), you need to prove that it works correctly (of course, sometime the proof is obvious) Young CS 530 Ad. Algo. D&A Approximation Algorithms 3

• For heuristic, we also need to prove the performance of the algorithm. • You don’t want to give a bad approximation algorithm that sometime gives poor performance. Also, you don’t want to give a good approximation algorithm but show that a loose bound (i. e. not a tight bound) Young CS 530 Ad. Algo. D&A Approximation Algorithms 4

Maximum Programs Stored (PS) Problem • Optimization PS Problem: Given a set of n program and two storage devices. Let si be the amount of storage needed to store the ith program. Let L be the storage capacity of each disk. Determine the maximum number of these n programs that can be stores on the two disks (without splitting a program over the disks). Young CS 530 Ad. Algo. D&A Approximation Algorithms 5

• The decision PS problem is NPC PARTITION PS (you should try this!) • Approximation PS Algorithm // assume programs are sorted in nondecreasing order of program size, // i. e. s 1 s 2 … sn. // Put as many programs as you can in the 1 st disk, then go to the 2 nd disk. i = 0; c=0; // c count the number of stored program for j = 1 to 2 { sum = 0 while ( sum + si L ) { store ith program into jth device sum += si i++; c++ if i > n return } } Young CS 530 Ad. Algo. D&A Approximation Algorithms 6

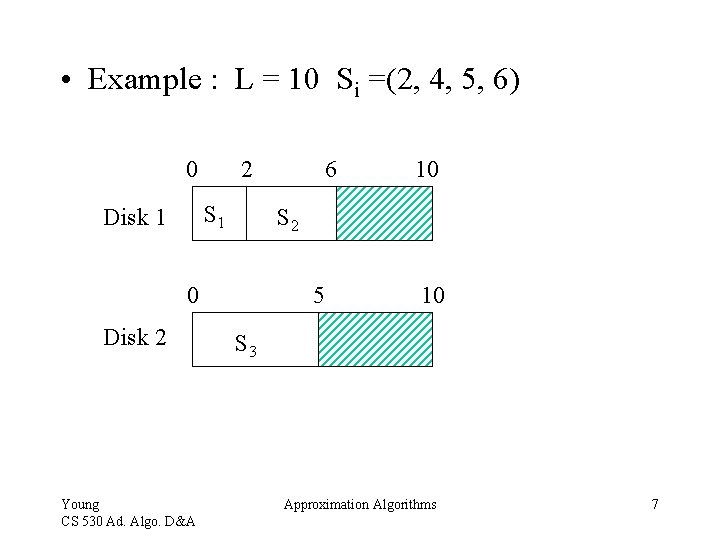
• Example : L = 10 Si =(2, 4, 5, 6) 0 2 S 1 Disk 1 Young CS 530 Ad. Algo. D&A 10 S 2 0 Disk 2 6 5 10 S 3 Approximation Algorithms 7

• Let C* be the optimal (maximum) number of programs that can be stores on the two disks. The above approximation PS algorithm gives very good performance ratio. C* <= (C + 1) OR C* C <= 1 + 1/C i. e. the given program stores at most 1 program less than the optimal solution Young CS 530 Ad. Algo. D&A Approximation Algorithms 8

Theorem The above approximation PS algorithm returns a number C such that C* (C + 1) where C* is the optimal value. Young CS 530 Ad. Algo. D&A Approximation Algorithms 9

• Theorem : The above approximation PS algorithm returns a number C such that C* (C + 1) where C* is the optimal value. a) It is easy to show that {s 1, s 2, …, sn} and L such that C* = (C + 1) The previous example gave C* = (C + 1) Young CS 530 Ad. Algo. D&A Approximation Algorithms 10

b) {s 1, s 2, …, sn} and L, C* (C + 1) Let’s consider only one disk with capacity 2 L. It is obvious that we can store maximum number of programs into the disk by considering programs in the order of s 1 s 2 … sn Let be the maximum number of programs that are stored in the disk Young CS 530 Ad. Algo. D&A Approximation Algorithms 11

Clearly C* and s 1 + s 2 + … + s 2 L Let j be an index such that (s 1 + s 2 + … + sj) L and (s 1 + s 2 + … + sj+1) > L (i) (ii) Obviously j and j programs are stored in the 1 st disk by the above approximation algorithm By (i) & (ii), (sj+2 + sj+3 + … + s ) L à (sj+1 + sj+2 + … + s -1) L at least (j+1)th program, (j+2)th program, …, ( -1)th program are stored in 2 nd disk by the above approximation alg. Done! Young CS 530 Ad. Algo. D&A Approximation Algorithms 12