Approximation algorithms for the TSP with a Parameterized









































- Slides: 52

Approximation algorithms for the TSP with a Parameterized Triangle Inequality Rotem Golan Alon Furman Department of Computer Science Ben-Gurion University

Outline 2

The Problem �An instance of the problem is a weighted graph G consisting on n vertices (representing cities). Distances between vertices satisfy the Δτ-inequality and the length of an optimal TSP tour is denoted OPT. �Δτ-inequality: dist(x, z) ≤ τ(dist(x, y) + dist(y, z)) �The objective of the problem is to find (in polynomial time) a tour having length at most f(τ)*OPT, where f(τ) is a slowly-growing function of τ. 3

�We observe two well known approximation algorithms for the TSP: �Double-Tree Algorithm 1. Find a minimum spanning tree T for G. 2. Create a multigraph by duplicating each edge in the MST. 3. Find an Eulerian tour. 4. Shortcut over nodes to obtain a Hamiltonian cycle. 4

�The above algorithm yields a 2 -approximation. 5



�Notice that step 4 in both algorithms obtains a Hamiltonian cycle by shortcutting the Eulerian tour. �In the TSP (satisfying the triangle inequality) the above step will always result in a shorter path, however, this is not the case for the Δτ-TSP! 50 x 10 15 y τ = 2 z dist(x, y) ≤ τ(dist(x, z) + dist(z, y)) ≤ 2 (15+10) ≤ 50 8


Outline 10

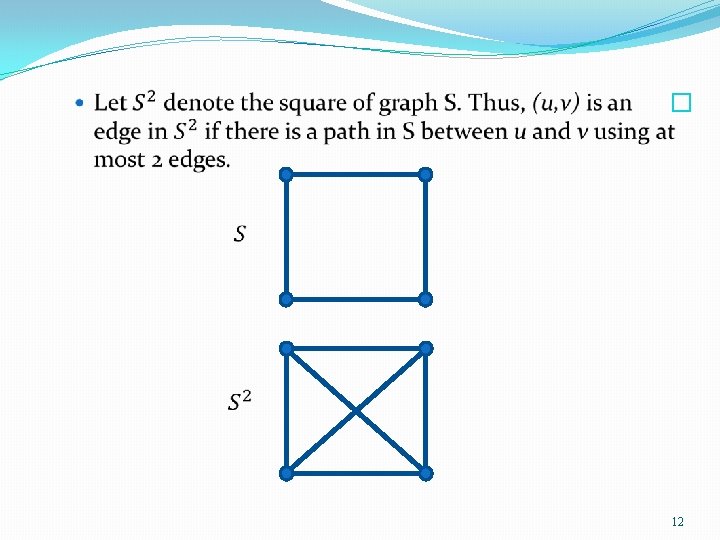
TSP-Approx �Definitions: �A graph S is 2 node connected if the deletion of any node from S leaves it connected. 11


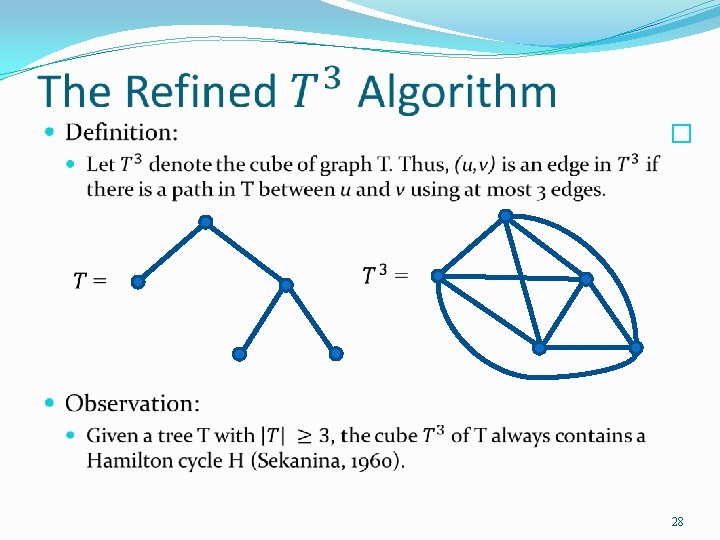
�Observations: 1. Any Hamiltonian cycle is 2 -node connected. Thus, the minimum weight 2 -node connected subgraph is a lower bound on OPT. 2. It is NP hard to find the minimum weight 2 -node connected subgraph. However, 2 approximation can be computed in polynomial time (Khuller & Raghavachari 1996, Penn & Shasha-Krupnik 1995). 3. The square of 2 -node connected graph contains a Hamilton cycle, which can be found in polynomial time (Fleischner 1970 , Lau 1980). 13

TSP-Approx Algorithm � 14



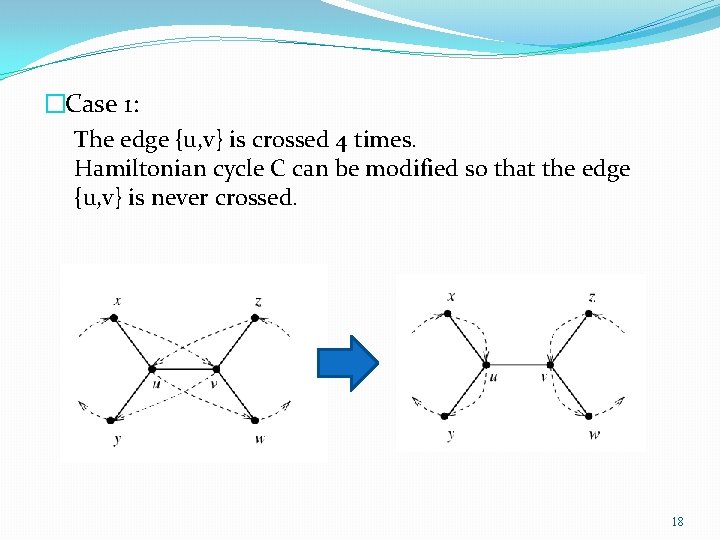
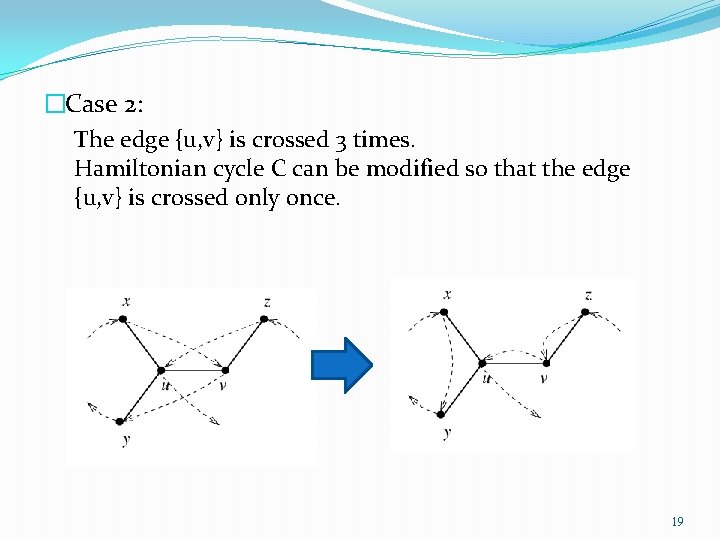
�Theorem 1: Algorithm TSP-Approx is a 4τ approximation algorithm. �We obtain a 4τ approximation by finding a new Hamiltonian cycle C’ that crosses every edge in S at most twice. �We obtain C’ by adjusting overlapping edges, there are 2 cases. 17

�Case 1: The edge {u, v} is crossed 4 times. Hamiltonian cycle C can be modified so that the edge {u, v} is never crossed. 18

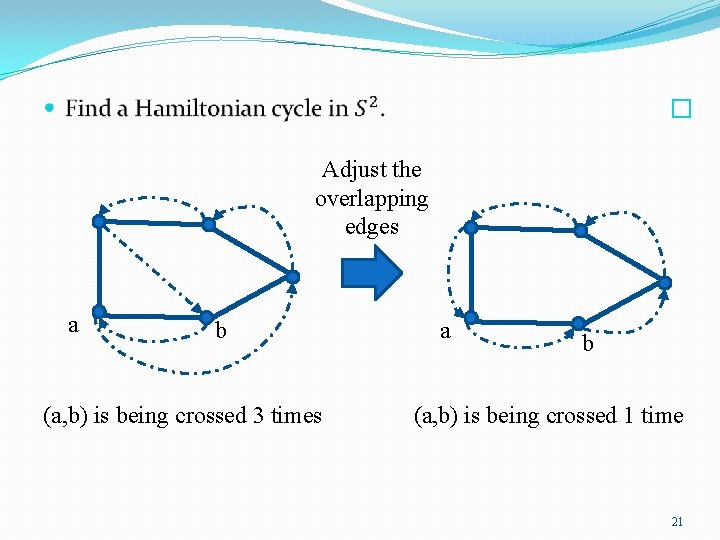
�Case 2: The edge {u, v} is crossed 3 times. Hamiltonian cycle C can be modified so that the edge {u, v} is crossed only once. 19

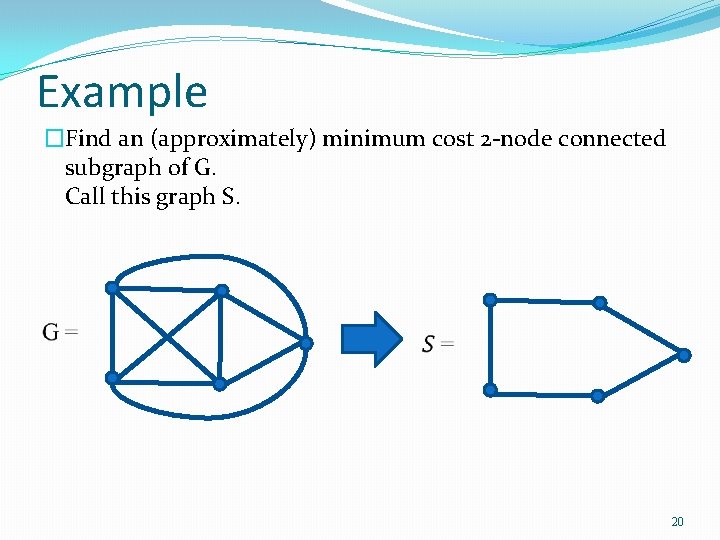
Example �Find an (approximately) minimum cost 2 -node connected subgraph of G. Call this graph S. 20

� Adjust the overlapping edges a b (a, b) is being crossed 3 times a b (a, b) is being crossed 1 time 21

Conclusions � 22

Outline 23



Conclusions � 26

Outline 27


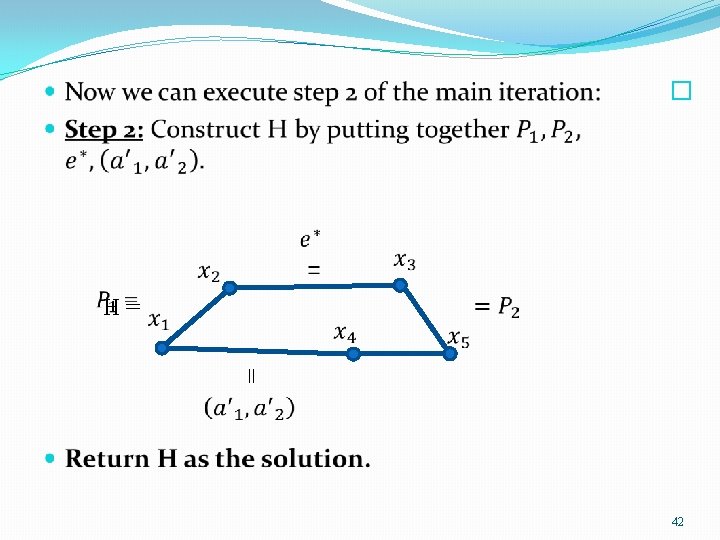
The Algorithm � 29




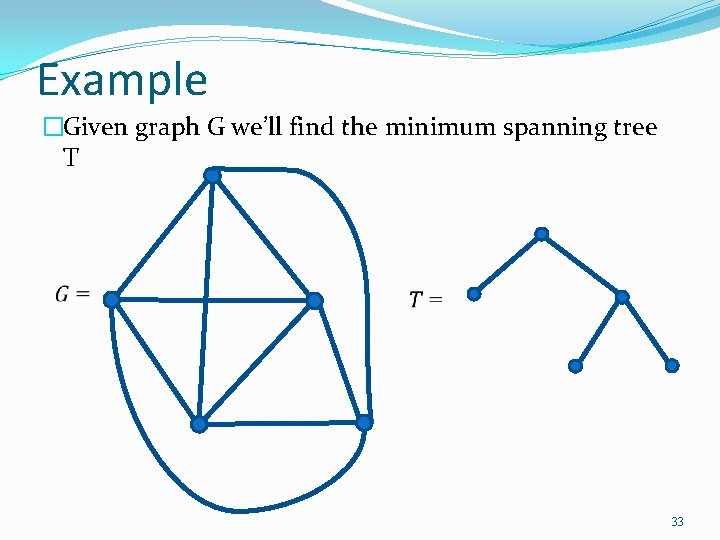
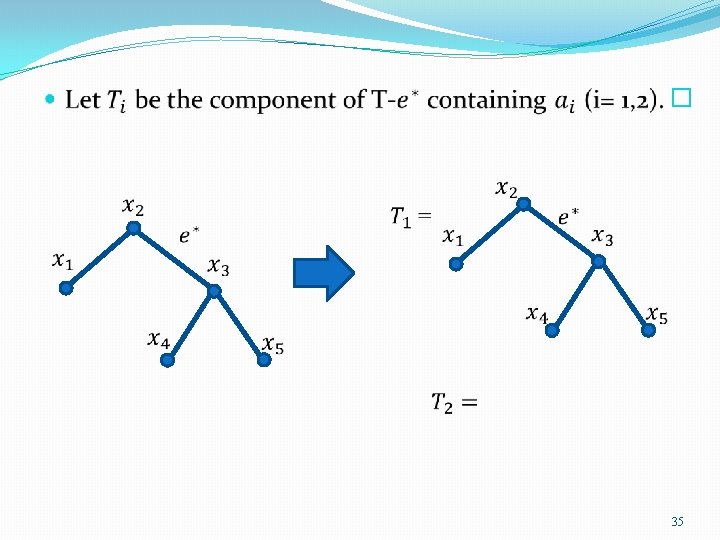
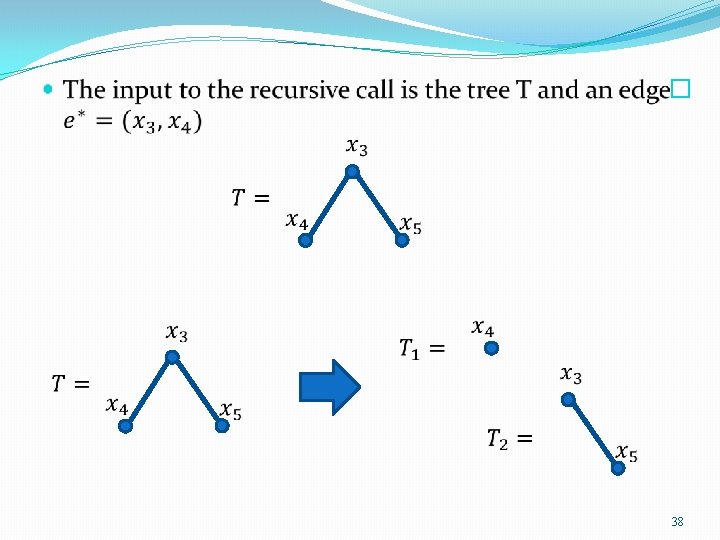
Example �Given graph G we’ll find the minimum spanning tree T 33

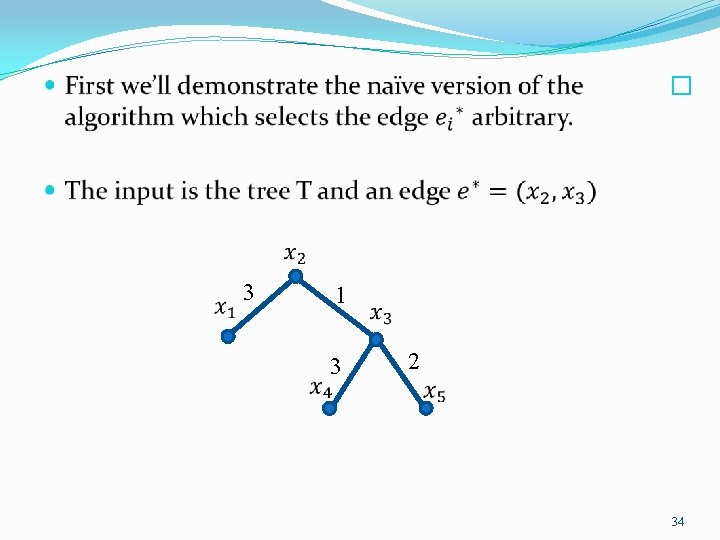
� 3 1 3 2 34










Outline 44

6 -approximation algorithm � 45

Why Euclidean TSP does not work in this case? � 46






Conclusion � 52