Approximation Algorithms for the Traveling Salesman Problem Shayan

Approximation Algorithms for the Traveling Salesman Problem Shayan Oveis Gharan

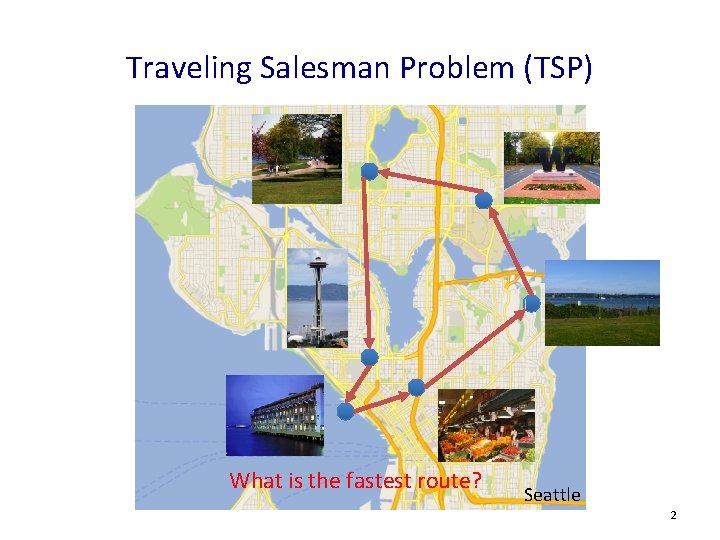
Traveling Salesman Problem (TSP) What is the fastest route? Seattle 2

Problem Formulation • May represent time, gas usage, … 3

Applications 4

Methods of Attack • Naïve Approach: Try all permutations! …. . #permutations of 75 cities >> #atoms in the universe 5

Methods of Attack • Naïve Approach: Try all permutations! • Optimistic Approach: Practical instances are easy TSP on the 2, 000 cities in the whole world 6

Methods of Attack • Naïve Approach: Try all permutations! • Optimistic Approach: Practical instances are easy Theory of Computing Approach: Find good solutions efficiently in the worst case. Bad scenarios happen in practice! 7

NP Completeness • 8

Approximation Algorithms • Run in time n or n 2 or n 3 9

Motivations for Worst case Approximation • 10

Approximation Algorithms for TSP 11

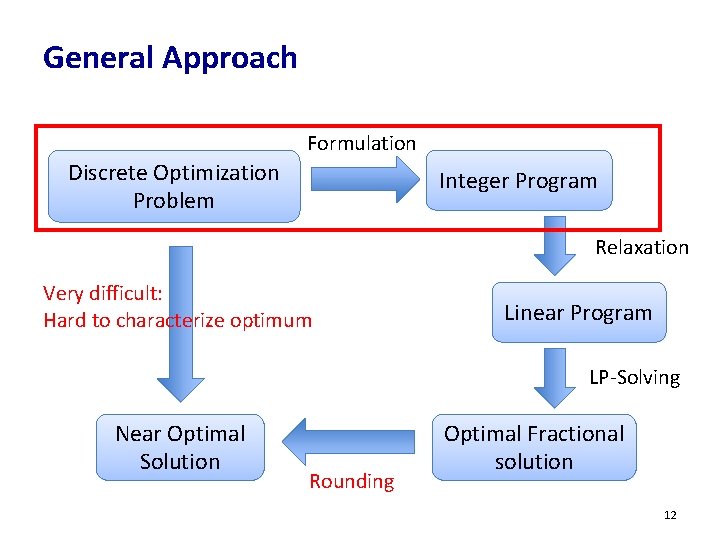
General Approach Formulation Discrete Optimization Problem Integer Program Relaxation Very difficult: Hard to characterize optimum Linear Program LP-Solving Near Optimal Solution Rounding Optimal Fractional solution 12

Formulation of the Optimum • 13

Integer Program • Cost of the solution Exit whenever Enter every subset of vertices Hard to solve Optimally 14

General Approach Formulation Discrete Optimization Problem Integer Program Relaxation Very difficult: Hard to characterize optimum Linear Program LP-Solving Near Optimal Solution Rounding Optimal Fractional solution 15

LP Relaxation Proposed by Dantzig, Fulkerson, Johnson 1954 and Held, Karp 1972. ! e l b i eas f s n i a m e mr u m i t Op 16

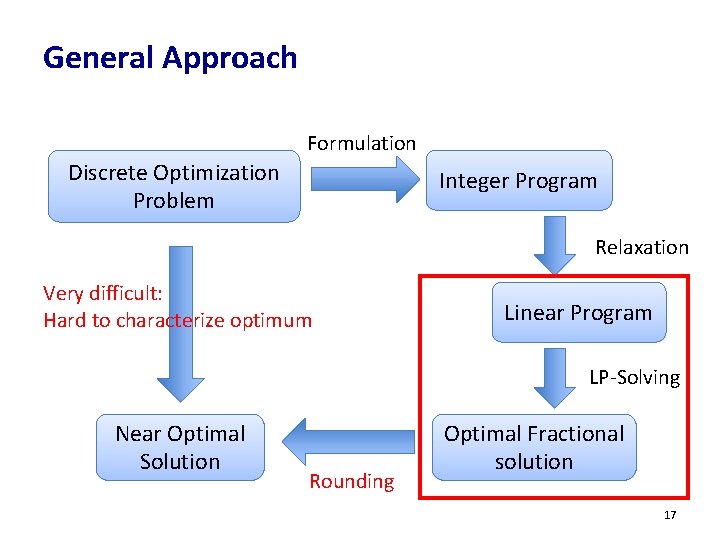
General Approach Formulation Discrete Optimization Problem Integer Program Relaxation Very difficult: Hard to characterize optimum Linear Program LP-Solving Near Optimal Solution Rounding Optimal Fractional solution 17

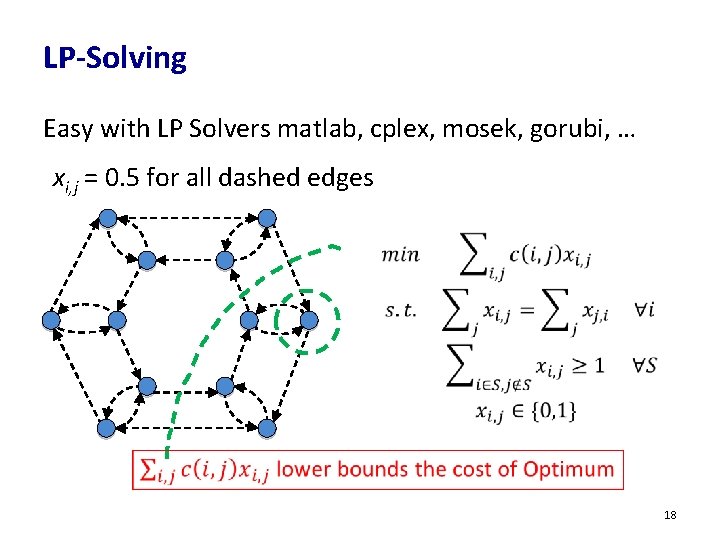
LP-Solving Easy with LP Solvers matlab, cplex, mosek, gorubi, … xi, j = 0. 5 for all dashed edges 18

General Approach Formulation Discrete Optimization Problem Integer Program Relaxation Very difficult: Hard to characterize optimum Linear Program LP-Solving Near Optimal Solution Rounding Optimal Fractional solution 19

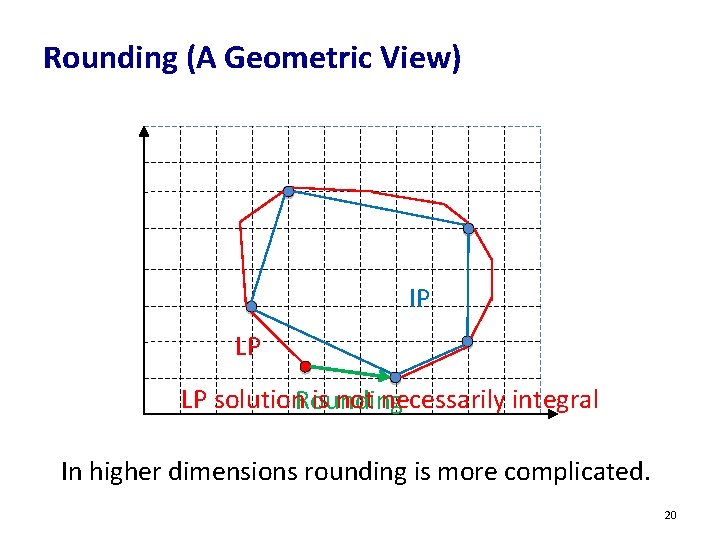
Rounding (A Geometric View) IP LP LP solution. Rounding is not necessarily integral In higher dimensions rounding is more complicated. 20

Rounding Can be quite complicated in the worst case. Easy in typical instances, because frac sols are sparse. 21

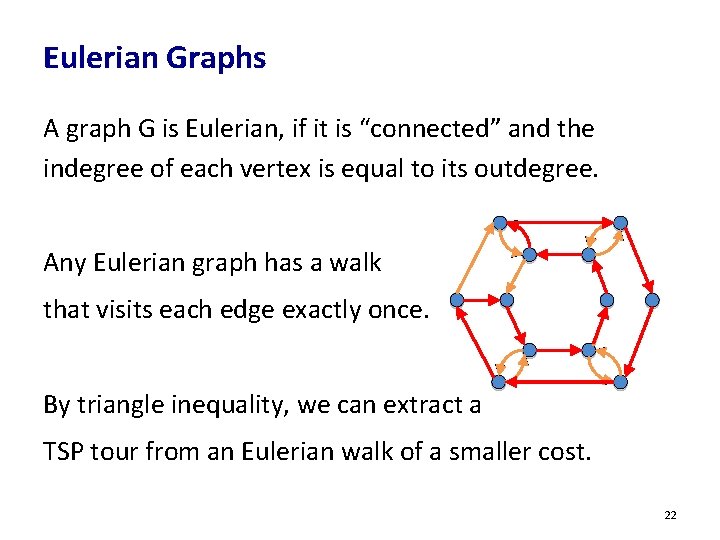
Eulerian Graphs A graph G is Eulerian, if it is “connected” and the indegree of each vertex is equal to its outdegree. Any Eulerian graph has a walk that visits each edge exactly once. By triangle inequality, we can extract a TSP tour from an Eulerian walk of a smaller cost. 22

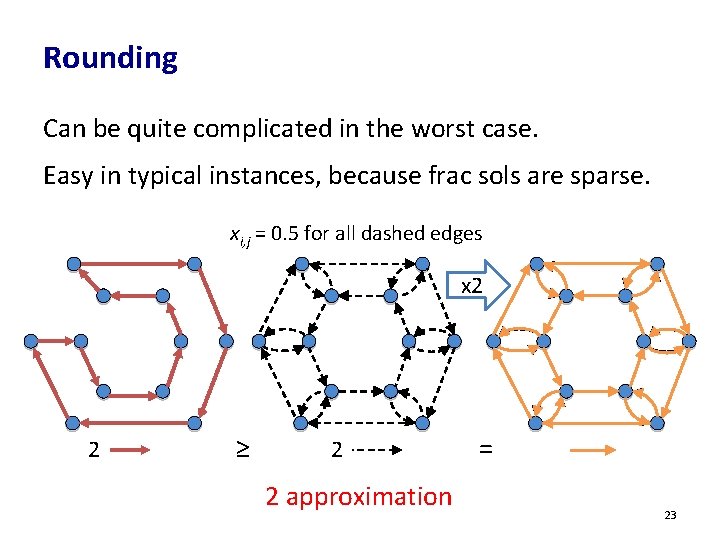
Rounding Can be quite complicated in the worst case. Easy in typical instances, because frac sols are sparse. xi, j = 0. 5 for all dashed edges x 2 2 ≥ 2 2 approximation = 23

Our Contribution Approximation Factor ] [FGM S] O M [AG us 10 00 90 82 Time 24

Conclusion • 25