Approximation Algorithms for Graph Routing Problems Julia Chuzhoy

Approximation Algorithms for Graph Routing Problems Julia Chuzhoy Toyota Technological Institute at Chicago

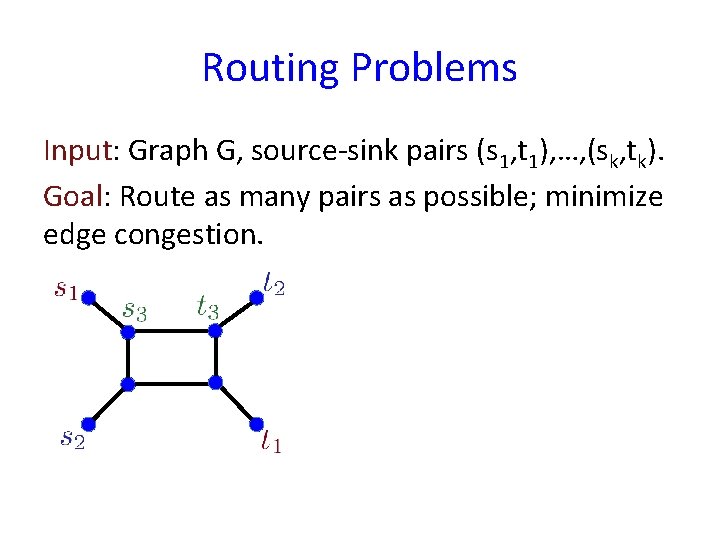
Routing Problems Input: Graph G, source-sink pairs (s 1, t 1), …, (sk, tk). Goal: Route as many pairs as possible; minimize edge congestion.

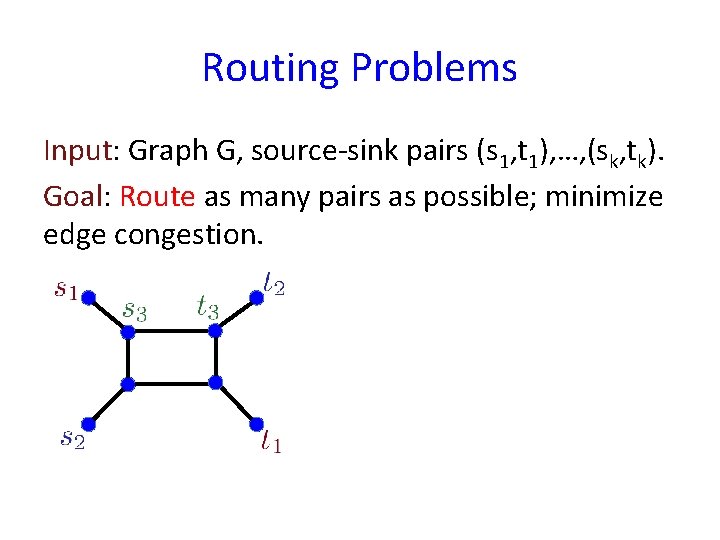
Routing Problems Input: Graph G, source-sink pairs (s 1, t 1), …, (sk, tk). Goal: Route as many pairs as possible; minimize edge congestion. Edge congestion: 2

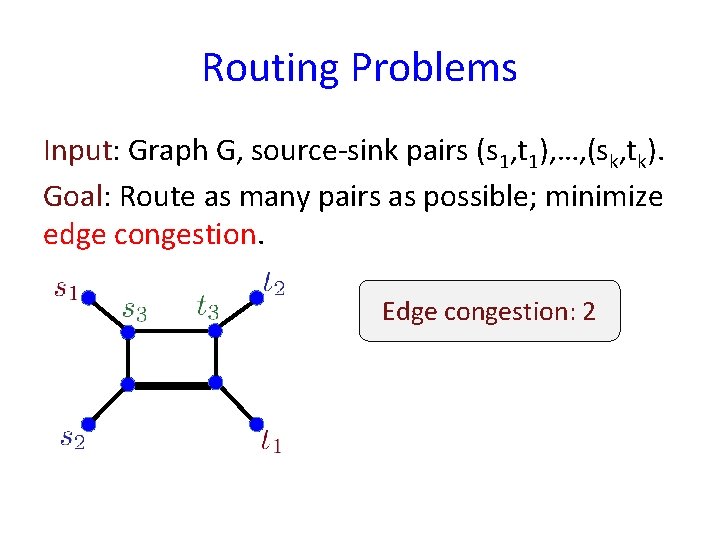
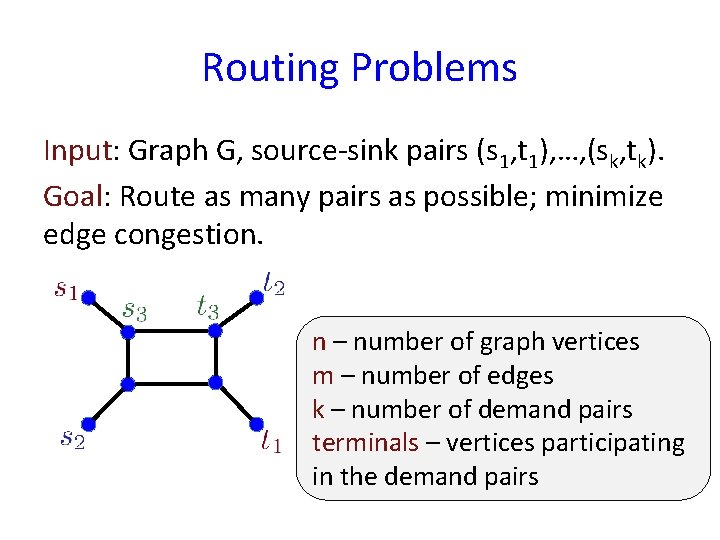
Routing Problems Input: Graph G, source-sink pairs (s 1, t 1), …, (sk, tk). Goal: Route as many pairs as possible; minimize edge congestion. n – number of graph vertices m – number of edges k – number of demand pairs terminals – vertices participating in the demand pairs

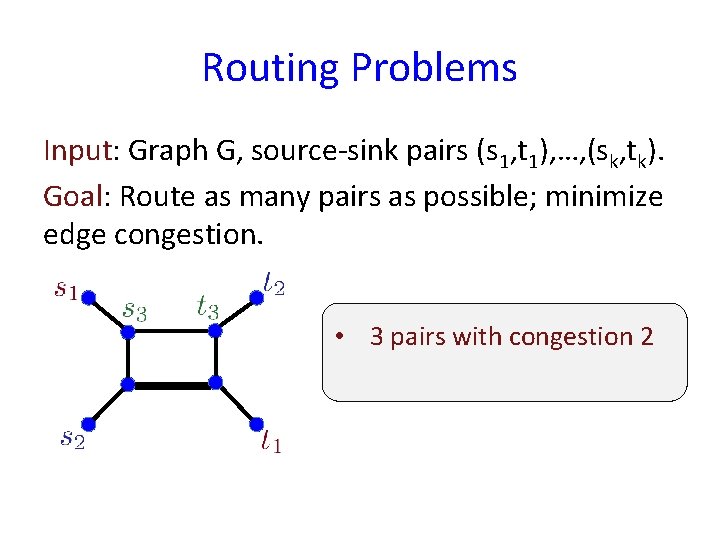
Routing Problems Input: Graph G, source-sink pairs (s 1, t 1), …, (sk, tk). Goal: Route as many pairs as possible; minimize edge congestion. • 3 pairs with congestion 2

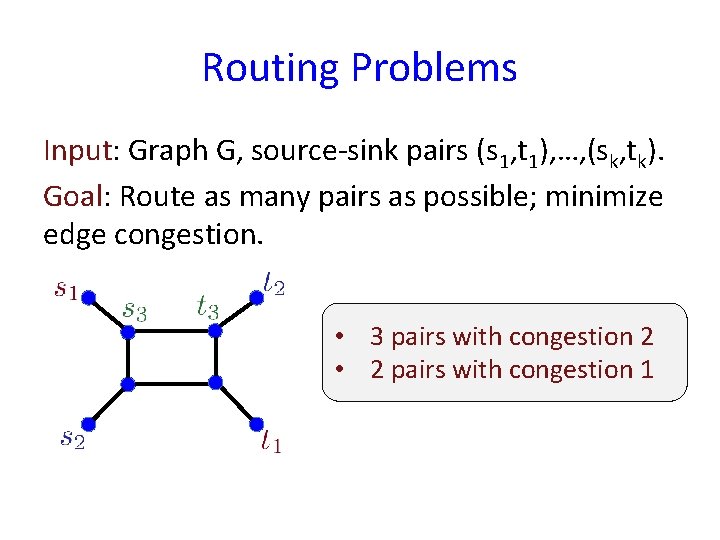
Routing Problems Input: Graph G, source-sink pairs (s 1, t 1), …, (sk, tk). Goal: Route as many pairs as possible; minimize edge congestion. • 3 pairs with congestion 2 • 2 pairs with congestion 1

Congestion Minimization

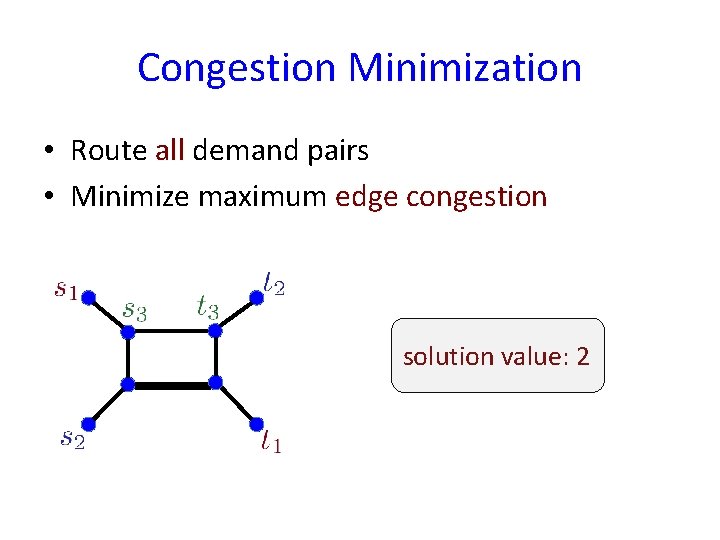
Congestion Minimization • Route all demand pairs • Minimize maximum edge congestion solution value: 2

LP-relaxation Rounding Algorithm [Raghavan, Thompson ‘ 87] • Every pair (si, ti) chooses a path P w. probability f(P) • Max edge congestion O(c log n/log n) w. h. p.

Congestion Minimization • Thompson ‘ 87] -approximation [Raghavan, • Directed graphs: -hard to approximate [Andrews, Zhang ‘ 06], [C, Guruswami, Khanna, Talwar ‘ 07] • Undirected graphs: -hard to approximate [Andrews, Zhang ‘ 07]

Open Problem 1 Can we close the gap for undirected graphs? • What is the integrality gap of the LP? • What if we only need to connect a constant fraction of the demand pairs?

Edge-Disjoint Paths Problem • No congestion allowed • Route maximum number of the demand pairs Solution value: 2

Edge Disjoint Paths (EDP) • For directed graphs NP-hard even with only two demand pairs [Fortune, Hopcroft, Wyllie '80] • When k is constant, can be solved efficiently in undirected graphs [Robertson, Seymour ‘ 90] • NP-hard when k is part of input [Karp ’ 72]

LP-relaxation

Rounding Algorithm [Kolliopoulos, Stein ‘ 98] • Find shortest path P with non-zero flow, connecting any demand pair. • Add P to the solution and delete all flow that uses edges of P. -approximation Analysis • If the length of P is less than flow is deleted. • If the length of P is more than flow remains. – at most

Can We Do Better? Directed graphs: EDP is -hard to approximate for any [Guruswami, Khanna, Rajaraman, Shepherd, Yannakakis ‘ 99] Undirected graphs: -approximation algorithm [Chekuri, Khanna, Shepherd ’ 06]. • -hardness of approximation for any[Andrews, Zhang ‘ 05], [Andrews, C, Guruswami, Khanna, • Talwar, Zhang ’ 10] • LP integrality gap: ‘ 93] [Garg, Vazirani, Yannakakis

Integrality Gap Example [Garg, Vazirani, Yannakakis ‘ 93] t 1 t 2 … tk s 1 s 2 … sk • fractional: k/2 • integral: 1 • k=

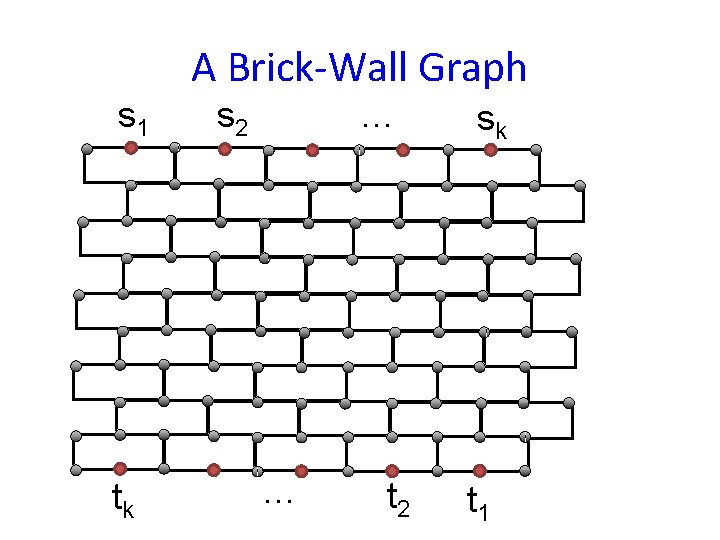
A Brick-Wall Graph s 1 tk … s 2 … t 2 sk t 1

Open Problem 2 Close the gap for undirected EDP • planar graphs? – constant-factor approximation with congestion 2 [Chekuri, Khanna, Shepherd ‘ 04], [Chekuri, Khanna, Shepherd ‘ 06], [Seguin-Charbonneau, Shepherd ‘ 11] – O(log n)-approximation for Eulerian or 4 -edge connected planar graphs [Kawarabayashi, Kobayashi ’ 10] – constant approximation for grid-like graphs [Kleinberg, Tardos ’ 95]

Open Problem 2 Close the gap for undirected EDP • planar graphs? • better algorithms for brick-wall graphs?

Positive Results Moderately connected graphs: If global min-cut is Ω(log 5 n), there is a polylog-approximation [Rao, Zhou ‘ 10] Expander graphs In a strong enough constant-degree expander, any demand set on vertices can be routed on edge-disjoint paths [Frieze ‘ 00] …

Edge Disjoint Paths (EDP) Congestion Minimization Route maximum number of pairs on edge-disjoint paths Route all pairs; minimize congestion • -approximation • matching integrality gap • • -hardness • -approximation -hardness EDP with Congestion (EDPw. C) A factor- approximation algorithm with congestion c routes. demand pairs with congestion at most c. optimum number of pairs with no congestion allowed

EDPw. C • Congestion O(log n/log n): constant approximation [Raghavan, Thompson ’ 87] • -approximation with congestion c [Azar, Regev ’ 01], [Baveja, Srinivasan ’ 00], [Kolliopoulos, Stein ‘ 04] Directed graphs: -hardness for any congestion c [C, Guruswami, Khanna, Talwar ’ 06]

EDPw. C • Congestion O(log n/log n): constant approximation [Raghavan, Thompson ’ 87] • -approximation with congestion c [Azar, Regev ’ 01], [Baveja, Srinivasan ’ 00], [Kolliopoulos, Stein ‘ 04] • polylog(n)-approximation with congestion poly(log n) [Andrews ‘ 10] • Congestion 2: -approximation [Kawarabayashi, Kobayashi ’ 11] • polylog(k)-approximation with congestion 14 [C, ‘ 11] • polylog(k)-approximation with congestion 2 [C, Li, ‘ 12]

Integrality Gaps for EDPw. C • Congestion 1: integrality gap [Garg, Vazirani, Yannakakis ‘ 93] • Congestion c: integrality gap [Andrews, C, Guruswami, Khanna, Talwar, Zhang ‘ 10] • -hard to approximate with t 1 congestion c for any t 2 … tk s 1 s 2 … sk

Edge Disjoint Paths (EDP) Congestion Minimization Route maximum number of pairs on edge-disjoint paths Route all pairs; minimize congestion • -approximation • matching integrality gap • -hardness • • -approximation -hardness EDP with Congestion (EDPw. C) • polylog(k)-approximation with congestion 2 • -hardness with congestion c

Another View: Reducing Congestion • Suppose we have a “bad” solution, where X pairs are routed with congestion C. • Then we can route X/(C polylog k) pairs with congestion 2! • But if we want congestion 1, may only be able to route pairs, even if C=2.

A Polylogarithmic Approximation with Constant Congestion

Well-Linkedness [Robertson, Seymour], [Chekuri, Khanna, Shepherd], [Raecke] Graph G is well-linked for the set T of terminals, iff for any partition (A, B) of V(G),

Pre-Processing Input: Graph G, source-sink pairs (s 1, t 1), …, (sk, tk). Theorem [Chekuri, Khanna Shepherd ‘ 04] Can efficiently partition G into disjoint subgraphs G 1, …, to. Gsolve that: “Enough” the problem on wellr, such linked instances. Gi the terminals • For each induced sub-problem are well-linked • Total fractional solution value for all induced sub-problems is

High-Level Plan [CKS ‘ 04] 1. Embed an expander on a subset of terminals into G. Crossbar – expander vertices – expander edges terminals paths in G 2. Route a subset of the demand pairs in the Embedding congestion: max load on any edge of G expander

$Goal Embed an expander over a subset of terminals into G. • Include polylog(k)-fraction$

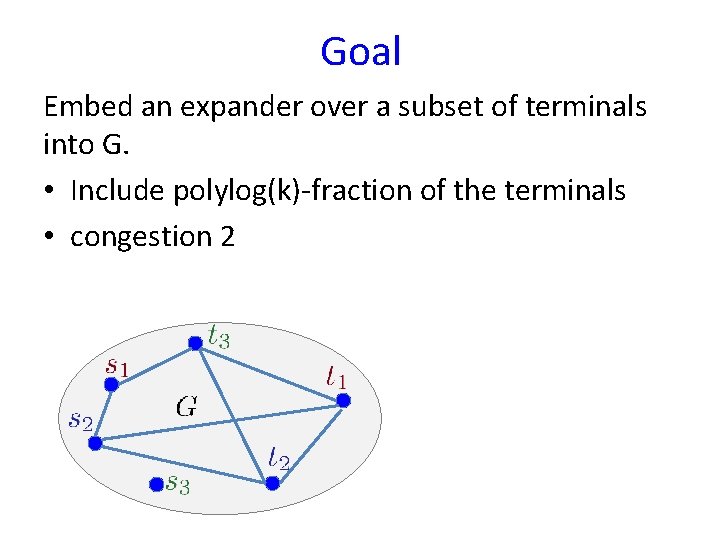
Goal Embed an expander over a subset of terminals into G. • Include polylog(k)-fraction of the terminals • congestion 2

Cut-Matching Game [Khandekar, Rao, Vazirani ’ 06] Cut Player: wants to build an expander Matching Player: wants to delay its construction There is a strategy for cut player, s. t. after O(log 2 n) iterations, we get an expander!

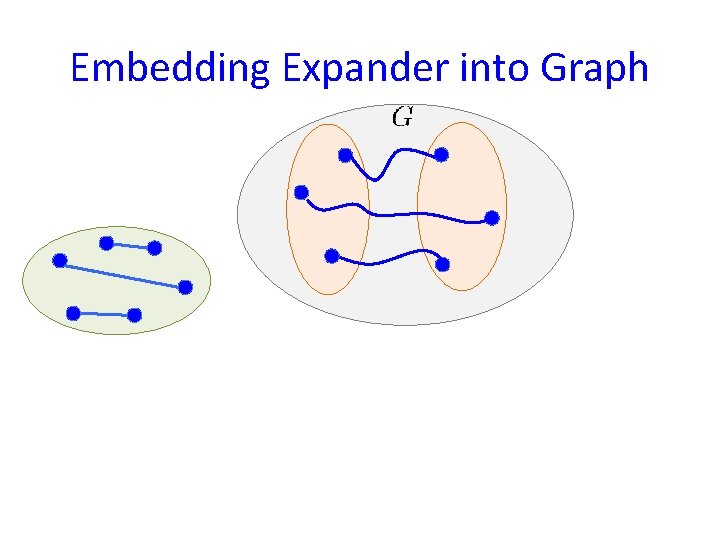
Embedding Expander into Graph

Embedding Expander into Graph After O(log 2 k) iterations, we get an expander embedded into G. Problem: congestion Ω(log 2 k)

Solution? Idea [Rao Zhou ‘ 06]: • Split G into graphs G 1, …, Gh using algorithm of [Karger ’ 93] – – V(Gi)=V(G) for all i Every edge of G belongs to at most one Gi Each Gi well-linked for the terminals h=O(log 2 k) • Run the cut-matching game. Use Gi to route flow in iteration i. Problem: Can only do it if min-cut in G is Ω(log 5 n) • [Andrews ‘ 10] adapted this to general graphs, with congestion poly(log n)

Getting a Constant Congestion

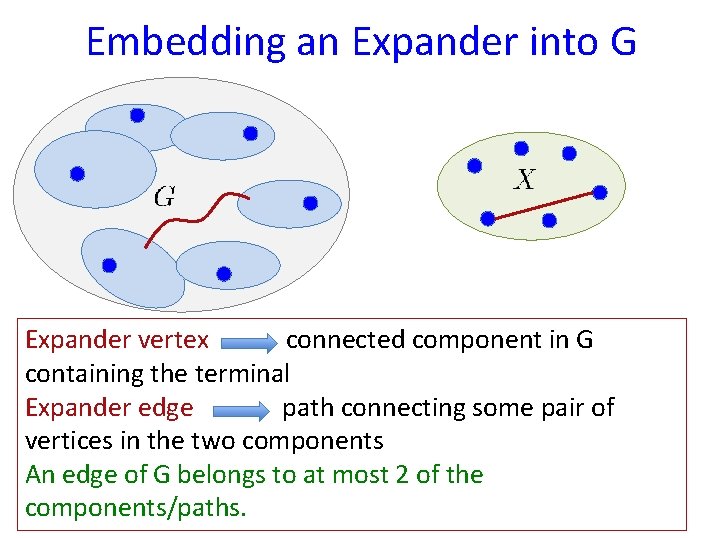
Embedding an Expander into G Expander vertex connected component in G containing the terminal Expander edge path connecting some pair of vertices in the two components An edge of G belongs to at most 2 of the components/paths.

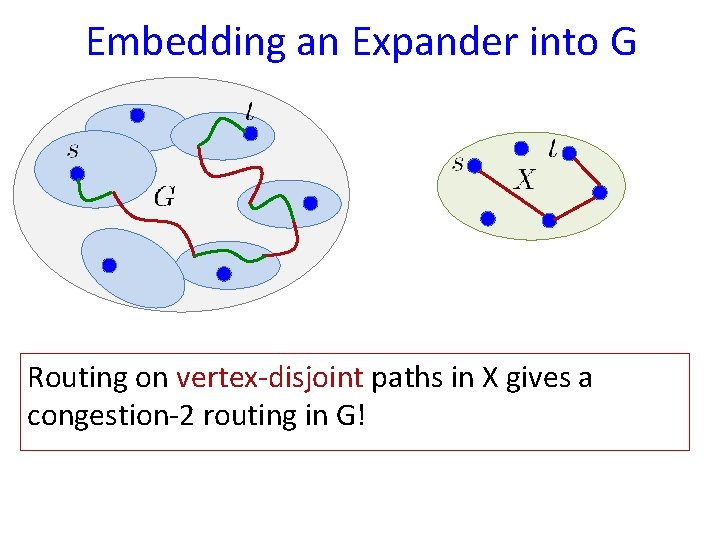
Embedding an Expander into G Routing on vertex-disjoint paths in X gives a congestion-2 routing in G!

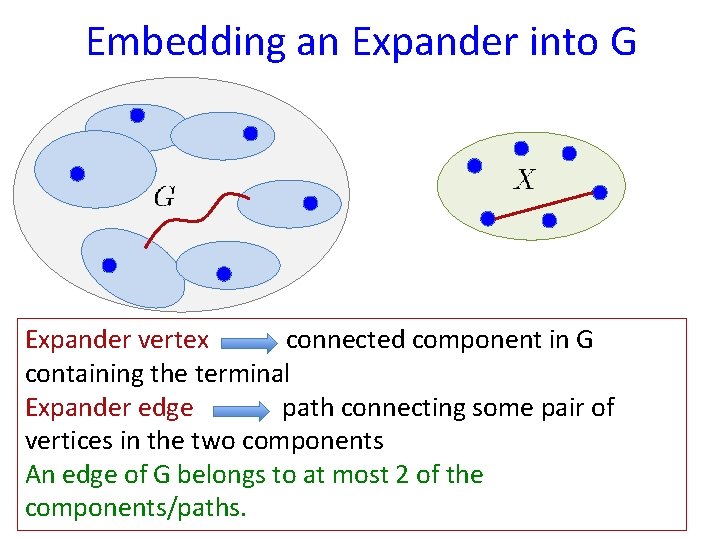
Embedding an Expander into G Expander vertex connected component in G containing the terminal Expander edge path connecting some pair of vertices in the two components An edge of G belongs to at most 2 of the components/paths.

Embedding an Expander into G Families of Good Vertex Sets

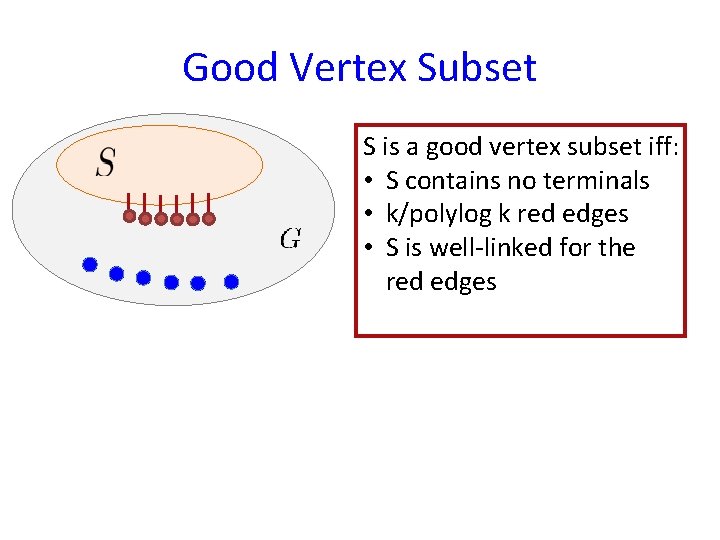
Good Vertex Subset S is a good vertex subset iff: • S contains no terminals • k/polylog k red edges • S is well-linked for the red edges

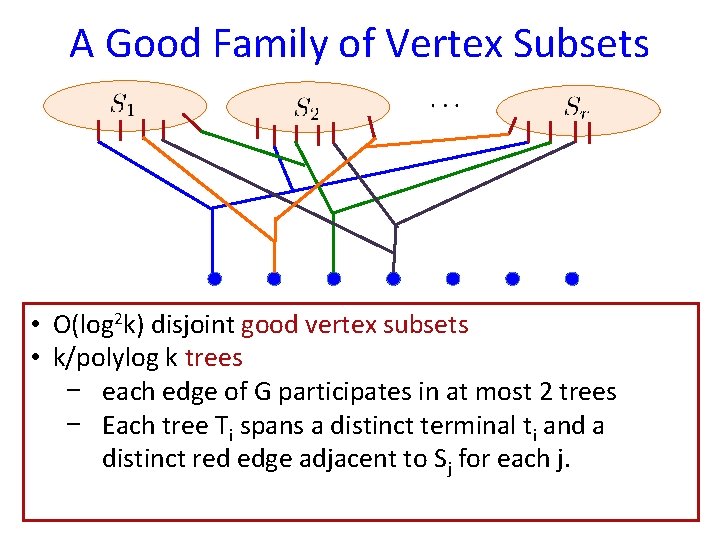
A Good Family of Vertex Subsets • O(log 2 k) disjoint good vertex subsets • k/polylog k trees − each edge of G participates in at most 2 trees − Each tree Ti spans a distinct terminal ti and a distinct red edge adjacent to Sj for each j.

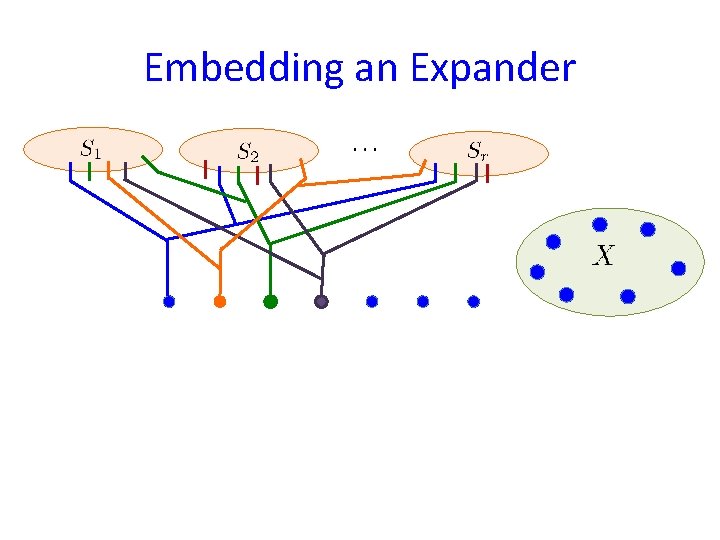
Embedding an Expander

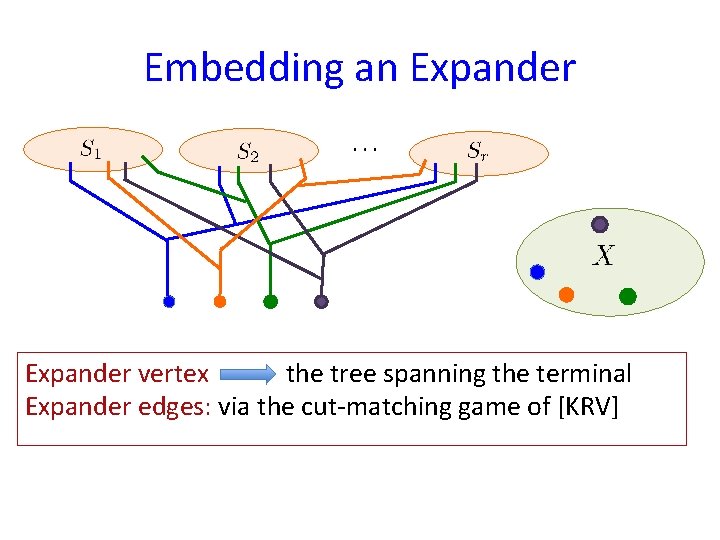
Embedding an Expander vertex the tree spanning the terminal Expander edges: via the cut-matching game of [KRV]

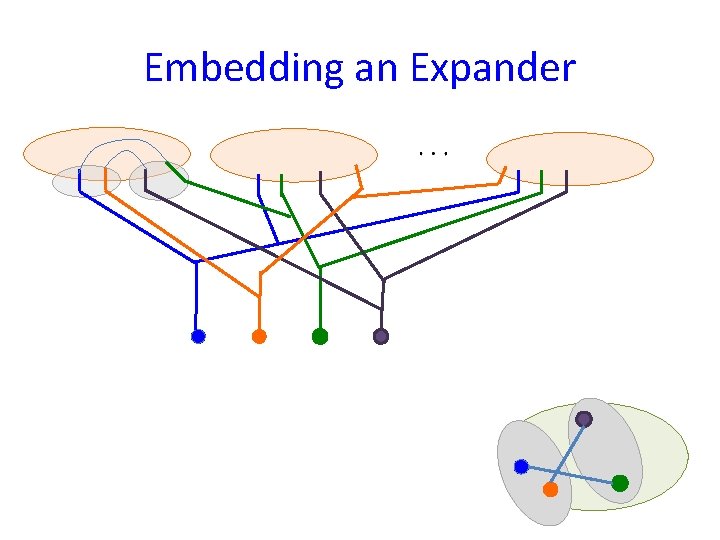
Embedding an Expander

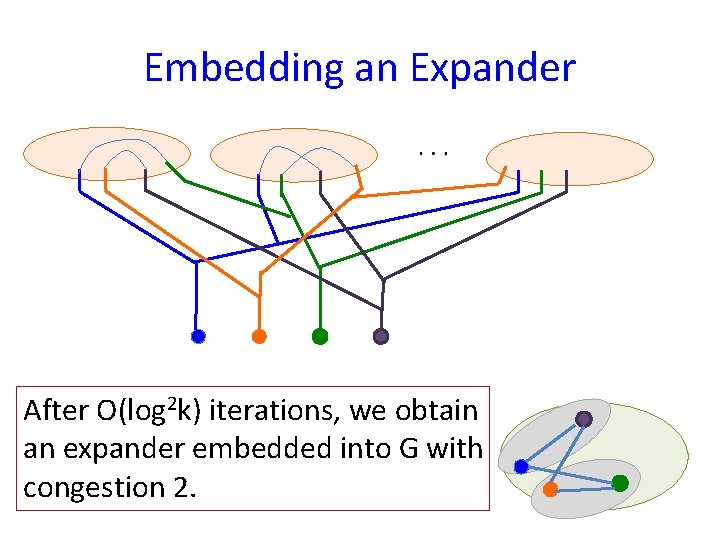
Embedding an Expander After O(log 2 k) iterations, we obtain an expander embedded into G with congestion 2. …

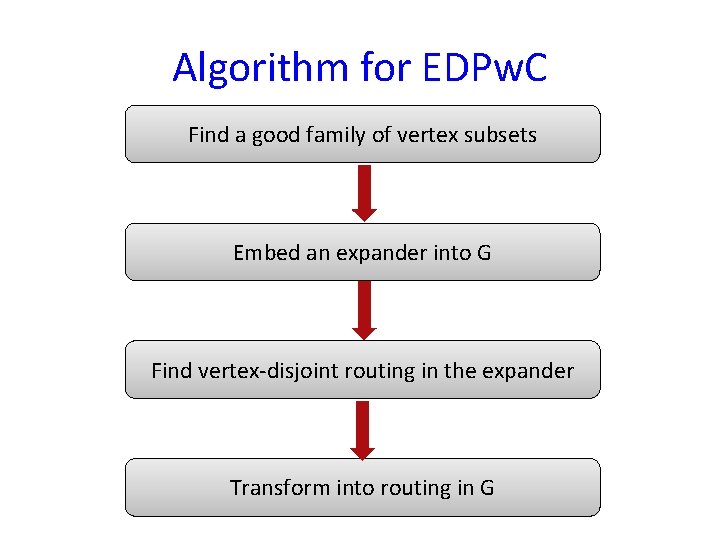
Algorithm for EDPw. C Find a good family of vertex subsets Embed an expander into G Find vertex-disjoint routing in the expander Transform into routing in G

Open Problem 3 • A cleaner algorithm for polylog(k) approximation with congestion 2? Better power of polylog? • What if we need to route almost all demand pairs (a constant fraction)?

Routing on Vertex-Disjoint Paths • Generalizes EDP • Connections to Graph Minor theory No congestion: • -approximation [Kolliopoulos, Stein ‘ 98] • -lower bound on LP integrality gap [Garg, Vazirani, Yannakakis ‘ 97] Routing with congestion: • O(poly log k)-approximation with constant congestion [Chekuri, Ene ‘ 12]

Open Problem 4 • Better algorithms/lower bounds for Vertex. Disjoint Paths?

Open Problem 4 • Better algorithms/lower bounds for Vertex. Disjoint Paths? • Vertex-disjoint paths in grid graphs

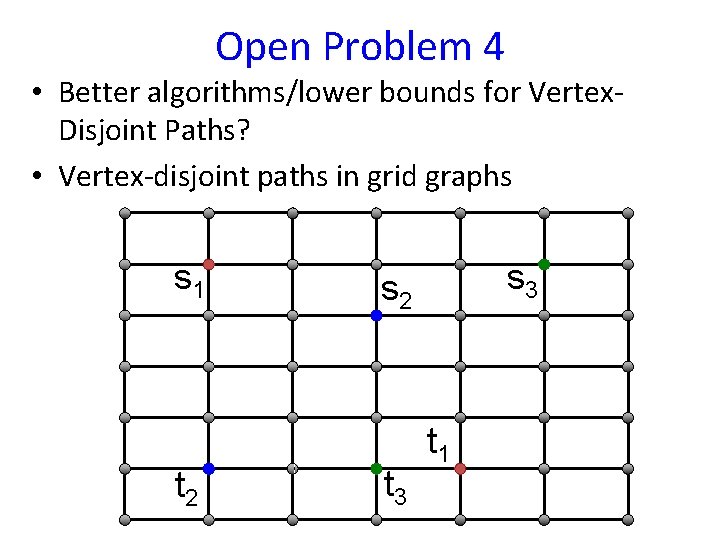
Open Problem 4 • Better algorithms/lower bounds for Vertex. Disjoint Paths? • Vertex-disjoint paths in grid graphs s 1 t 2 s 3 s 2 t 3 t 1

Thank you!