Approximation Algorithms Chapter 1 Introduction General Information Time

Approximation Algorithms Chapter 1 - Introduction

General Information Ø Time: MWF 1: 55 – 2: 45 Ø Place: TUR 2303 My T. Thai mythai@cise. ufl. edu 2

Instructor Information q q q Name: Dr. My T. Thai Office: E 566 CSE Building Phone: (352)392 -6842 Email: mythai@cise. ufl. edu Office Hours: W 3: 00 pm – 5: 00 pm or by appointments My T. Thai mythai@cise. ufl. edu 3

Why Approximation Algorithms Ø Problems that we cannot find an optimal solution in a polynomial time q Eg: Set Cover, Bin Packing Ø Need to find a near-optimal solution: q Heuristic q Approximation algorithms: § This gives us a guarantee approximation ratio My T. Thai mythai@cise. ufl. edu 4

Why take this course Ø Your advisers/bosses give you a computationally hard problem. Here are two scenarios: q No knowledge about approximation: § Spend a few months looking for an optimal solution § Come to their office and confess that you cannot do it § Get fired q Knowledge about approximation: My T. Thai mythai@cise. ufl. edu 5

Why take this course (cont) Ø Knowledge about approximation q Show your boss that this is a NP-complete (NPhard) problem q There does not exist any polynomial time algorithm to find an exact solution q Propose a good algorithm (either heuristic or approximation) to find a near-optimal solution q Better yet, prove the approximation ratio My T. Thai mythai@cise. ufl. edu 6

Course Description Ø Covers a variety of techniques to design and analyze many approximation algorithms for computationally hard problems: q Combinatorial algorithms: § Greedy Techniques, Independent System, Submodular Function § Cover various problems q Linear Programming based algorithms q Semidefinite Programming based algorithms My T. Thai mythai@cise. ufl. edu 7

Course Objectives Ø Grasp the essential techniques to design and analyze approximation algorithms: q q q Combinatorial methods Linear programming Semidefinite programming Primal-dual and relaxation methods Hardness of approximation Ø Grasp the key ideas of graph theory Ø Able to model and solve many practical problems raising in. Myour real life T. Thai mythai@cise. ufl. edu 8

Textbooks Ø Required: q Vijay Vazirani, Approximation Algorithms, Springer-Verlag, 2001 Ø Recommended: q Vasek Chvatal, Linear Programming, W. H. Freeman Company q Michael R. Garey and David S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness Ø Shall provide some appropriate lecture notes My T. Thai mythai@cise. ufl. edu 9

Grading Policies Ø Homework Assignments: q 5 homework assignments, each weighs 10% q Due at the beginning of the lecture on the due date q No late assignment will be accepted Ø Midterm Exam: q One midterm exam, weighs 20% q In class, open book, open notes Ø One Final Exam: q Weighs 30% My T. Thai mythai@cise. ufl. edu 10

Grading Policies (cont) Cut-off points: q A >= 85% q 85% > B >= 75% q 75% > C >= 65% My T. Thai mythai@cise. ufl. edu 11

Plagiarism Policy Ø Zero tolerance Ø Collaboration: q May discuss with other students on homework, but must write up solution on your own independently Ø More info, see the class website Ø Other policy: Students are encouraged to attend the class. Many proofs will not be shown on the lecture slides My T. Thai mythai@cise. ufl. edu 12

Tentative Schedule Ø See the class website for detail information Ø Roughly divided into two parts: q Week 1 to Week 8: Combinatorial Algorithms q Week 9 to Week 16: Linear Programming: Dual. Primal, Relaxation, Rounding, and Semidefinite programming My T. Thai mythai@cise. ufl. edu 13

Introduction to Combinatorial Optimization My T. Thai mythai@cise. ufl. edu 14

Combinatorial Optimization Ø The study of finding the “best” object from within some finite space of objects, eg: q Shortest path: Given a graph with edge costs and a pair of nodes, find the shortest path (least costs) between them q Traveling salesman: Given a complete graph with nonnegative edge costs, find a minimum cost cycle visiting every vertex exactly once q Maximum Network Lifetime: Given a wireless sensor networks and a set of targets, find a schedule of these sensors to maximize network lifetime My T. Thai mythai@cise. ufl. edu 15

In P or not in P? Informal Definitions: Ø The class P consists of those problems that are solvable in polynomial time, i. e. O(nk) for some constant k where n is the size of the input. Ø The class NP consists of those problems that are “verifiable” in polynomial time: q Given a certificate of a solution, then we can verify that the certificate is correct in polynomial time My T. Thai mythai@cise. ufl. edu 16

In P or not in P: Examples Ø In P: q Shortest path q Minimum Spanning Tree Ø Not in P (NP): q Vertex Cover q Traveling salesman q Minimum Connected Dominating Set My T. Thai mythai@cise. ufl. edu 17

NP-completeness (NPC) Ø A problem is in the class NPC if it is in NP and is as “hard” as any problem in NP My T. Thai mythai@cise. ufl. edu 18

What is “hard” Ø Decision Problems: Only consider YES-NO q Decision version of TSP: Given n cities, is there a TSP tour of length at most L? Ø Why Decision Problem? What relation between the optimization problem and its decision? q Decision is not “harder” than that of its optimization problem q If the decision is “hard”, then the optimization problem should be “hard” My T. Thai mythai@cise. ufl. edu 19

NP-complete and NP-hard A language L is NP-complete if: 1. L is in NP, and 2. For every L’ in NP, L’ can be polynomialtime reducible to L My T. Thai mythai@cise. ufl. edu 20

Approximation Algorithms Ø An algorithm that returns near-optimal solutions in polynomial time Ø Approximation Ratio ρ(n): q Define: C* as a optimal solution and C is the solution produced by the approximation algorithm q max (C/C*, C*/C) <= ρ(n) q Maximization problem: 0 < C <= C*, thus C*/C shows that C* is larger than C by ρ(n) q Minimization problem: 0 < C* <= C, thus C/C* shows that C is larger than C* by ρ(n) My T. Thai mythai@cise. ufl. edu 21

Approximation Algorithms (cont) Ø PTAS (Polynomial Time Approximation Scheme): A (1 + ε)-approximation algorithm for a NP-hard optimization П where its running time is bounded by a polynomial in the size of instance I Ø FPTAS (Fully PTAS): The same as above + time is bounded by a polynomial in both the size of instance I and 1/ε My T. Thai mythai@cise. ufl. edu 22

A Dilemma! Ø We cannot find C*, how can we compare C to C*? Ø How can we design an algorithm so that we can compare C to C* It is the objective of this course!!! My T. Thai mythai@cise. ufl. edu 23

Vertex Cover Ø Definition: Ø An Example My T. Thai mythai@cise. ufl. edu 24

Vertex Cover Problem Ø Definition: q Given an undirected graph G=(V, E), find a vertex cover with minimum size (has the least number of vertices) q This is sometimes called cardinality vertex cover Ø More generalization: q Given an undirected graph G=(V, E), and a cost function on vertices c: V → Q+ q Find a minimum cost vertex cover My T. Thai mythai@cise. ufl. edu 25

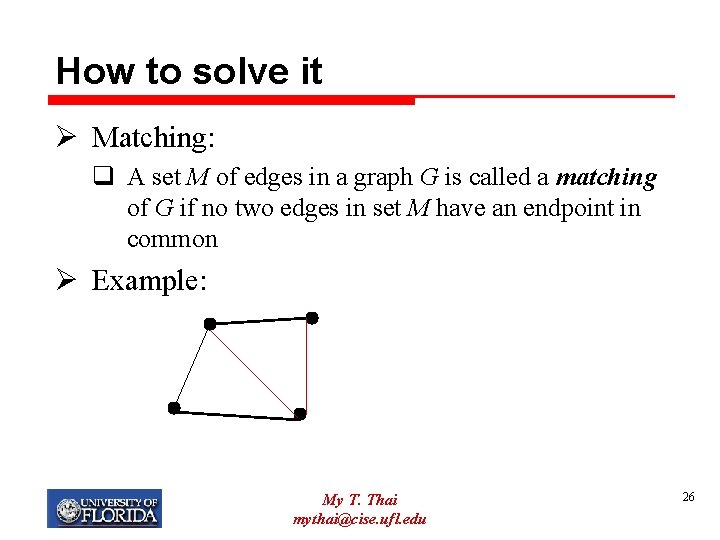
How to solve it Ø Matching: q A set M of edges in a graph G is called a matching of G if no two edges in set M have an endpoint in common Ø Example: My T. Thai mythai@cise. ufl. edu 26

How to solve it (cont) Ø Maximum Matching: q A matching of G with the greatest number of edges Ø Maximal Matching: q A matching which is not contained in any larger matching Ø Note: Any maximum matching is certainly maximal, but not the reverse My T. Thai mythai@cise. ufl. edu 27

Main Observation Ø No vertex can cover two edges of a matching Ø The size of every vertex cover is at least the size of every matching: |M| ≤ |C| Ø |M| = |C| indicates the optimality Ø Possible Solution: Using Maximal matching to find Minimum vertex cover My T. Thai mythai@cise. ufl. edu 28

An Algorithm Ø Alg 1: Find a maximal matching in G and output the set of matched vertices Ø Theorem: The algorithm 1 is a factor 2 -approximation algorithm. Ø Proof: My T. Thai mythai@cise. ufl. edu 29

Can Alg 1 be improved? Ø Q 1: Can the approximation ratio of Alg 1 be improved by a better analysis? Ø Q 2: Can we design a better approximation algorithm using the similar technique (maximal matching)? Ø Q 3: Is there any other lower bounding method that can lead to a better approximation algorithm? My T. Thai mythai@cise. ufl. edu 30

Answers Ø A 1: No by considering the complete bipartite graphs Kn, n Ø A 2: No by considering the complete graph Kn where n is odd. q |M| = (n-1)/2 whereas opt = n -1 My T. Thai mythai@cise. ufl. edu 31

Answers (cont) Ø A 3: q Currently a central open problem q Yes, we can obtain a better one by using the semidefinite programming Ø Generalization vertex Cover q Can we still able to design a 2 -approximation algorithm? q Homework assignment! My T. Thai mythai@cise. ufl. edu 32

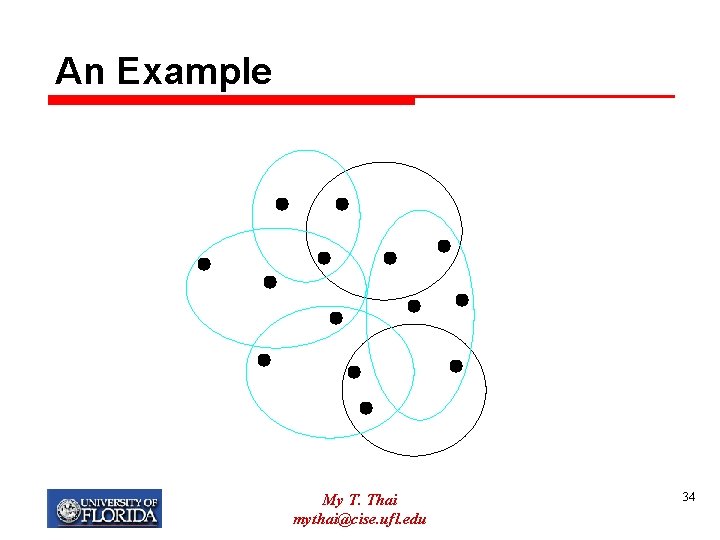
Set Cover Ø Definition: Given a universe U of n elements, a collection of subsets of U, S = {S 1, …, Sm}, and a cost function c: S → Q+, find a minimum cost subcollection C of S that covers all elements of U. Ø Example: q q U = {1, 2, 3, 4, 5} S 1 = {1, 2, 3}, S 2 = {2, 3}, S 3 = {4, 5}, S 4 = {1, 2, 4} c 1 = c 2 = c 3 = c 4 = 1 Solution C = {S 1, S 3} Ø If the cost is uniform, then the set cover problem asks us to find a subcollection covering all elements of U with the minimum size. My T. Thai mythai@cise. ufl. edu 33

An Example My T. Thai mythai@cise. ufl. edu 34

NP-completeness Ø Theorem: Set Cover (SC) is NP-complete Ø Proof: INSTANCE: Given a universe U of n elements, a collection of subsets of U, S = {S 1, …, Sm}, and a positive integer b QUESTION: Is there a such that , |C| ≤ b, (Note: The subcollection {Si | } satisfying the above condition is called a set cover of U My T. Thai mythai@cise. ufl. edu 35

Proof (cont) Ø First we need to show that SC is in NP. Given a collection of sets C, it is easy to verify that if |C| ≤ b and the union of all sets listed in C does include all elements in U. Ø To complete the proof, we need to show that Vertex Cover (VC) ≤p Set Cover (SC) Given an instance C of VC (an undirected graph G=(V, E) and a positive integer j), we need to construct an instance C’ of SC in polynomial time such that C is satisfiable iff C’ is satisfiable. My T. Thai mythai@cise. ufl. edu 36

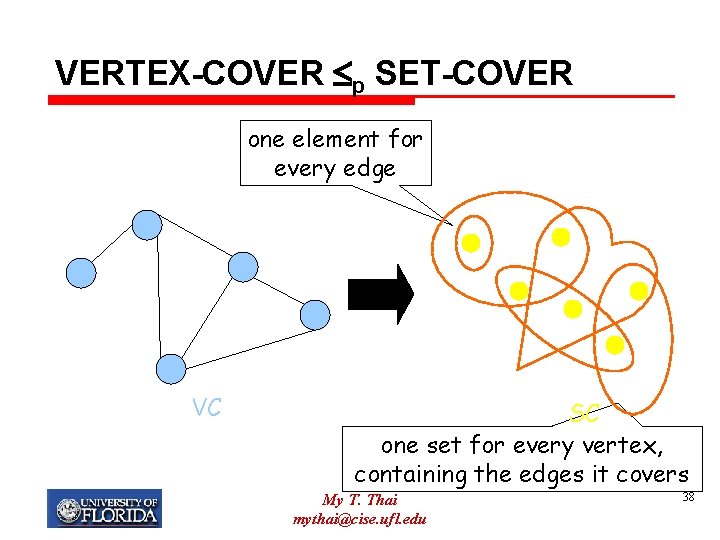
Proof (cont) Construction: Let U = E. We will define n elements of U and a collection S as follows: Label all vertices in V from 1 to n. Let Si be the set of all edges that incident to vertex i. Finally, let b = j. This construction is in poly-time with respect to the size of VC instance. Note: Each edge corresponds to each element in U and each vertex corresponds to each set in S. My T. Thai mythai@cise. ufl. edu 37

VERTEX-COVER p SET-COVER one element for every edge VC SC one set for every vertex, containing the edges it covers My T. Thai mythai@cise. ufl. edu 38

Proof (cont) Now, we need to prove that C is satisfiable iff C’ is. That is, we need to show that if the original instance of VC is a yes instance iff the constructed instance of SC is a yes instance. Ø (→) Suppose G has a vertex cover of size at most j, called C. By our construction, C corresponds to a collection C’ of subsets of U. Since b = j, |C’| ≤ b. Plus, C’ covers all elements in U since C “covers” all edges in G. To see this, consider any element of U. Such an element is an edge in G. Since C is a set cover, at least endpoint of this. Myedge is in C. T. Thai mythai@cise. ufl. edu 39

Ø (←) Suppose there is a set cover C’ of size at most b in our constructed instance. Since each set in C’ is associated with a vertex in G, let C be the set of these vertices. Then |C| = |C’| ≤ b = j. Plus, C is a vertex cover of G since C’ is a set cover. To see this, consider any edge e. Since e is in U, C’ must contain at least one set that includes e. By our construction, the only set that include e correspond to nodes that are endpoints of e. Thus C must contain at least one endpoints of e. My T. Thai mythai@cise. ufl. edu 40

Solutions Algorithm 1: (in the case of uniform cost) 1: C = empty 2: while U is not empty 3: pick a set Si such that Si covers the most elements in U 4: remove the new covered elements from U 5: C = C union Si 6: return C My T. Thai mythai@cise. ufl. edu 41

Solutions (cont) Ø In the case of non-uniform cost Ø Similar method. At each iteration, instead of picking a set Si such that Si covers the most uncovered elements, we will pick a set Si whose cost-effectiveness α is smallest, where α is defined as: Ø Questions: Why choose smallest α? Why define α as above My T. Thai mythai@cise. ufl. edu 42

Solutions (cont) Algorithm 2: (in the case of non-uniform cost) 1: C = empty 2: while U is not empty 3: pick a set Si such that Si has the smallest α 4: for each new covered elements e in U 5: set price(e) = α 6: remove the new covered elements from U 7: C = C union Si 8: return C My T. Thai mythai@cise. ufl. edu 43

Approximation Ratio Analysis Let ek, k = 1…n, be the elements of U in the order in which they were covered by Alg 2. We have: Ø Lemma 1: Ø Proof: Let Uj be the set the remaining set U at iteration j. That is, Uj contains all the uncovered elements at iteration j. At any iteration j, the leftover sets of the optimal solution can cover the remaining elements at a cost of at most opt. (Why? ) My T. Thai mythai@cise. ufl. edu 44

Proof of Lemma 1 (cont) Thus, among these leftover sets, there must exist one set where its α value is at most opt/|Uj|. Let ek be the element covered at this iteration, |Uj| ≥ n – k + 1. Since ek was covered by the most cost -effective set in this iteration, we have: price(ek) ≤ opt/|Uj| ≤ opt/(n-k+1) My T. Thai mythai@cise. ufl. edu 45

Approximation Ratio Ø Theorem 1: The set cover obtained form Alg 2 (also Alg 1) has a factor of Hn where Hn is a harmonic series Hn = 1 + 1/2 + … + 1/n Ø Proof: It follows directly from Lemma 1 My T. Thai mythai@cise. ufl. edu 46