Approximation Algorithms and Online Mechanisms for Item Pricing

Approximation Algorithms and Online Mechanisms for Item Pricing Maria-Florina Balcan & Avrim Blum CMU, CSD Maria-Florina Balcan

Revenue Maximization in Unlimited Supply Comb. Auctions with Single-minded Bidders • Imagine a supermarket trying to decide on how to price the goods it is selling (coffee, milk, sugar, oranges, apples. . . ). • Customers have shopping lists. Decide what to buy or whether to shop at all based on prices of items in list. – Customers buy everything or nothing based on sum of prices in list. • Seller’s Goal: set prices to maximize revenue. Maria-Florina Balcan

Supermarket Pricing Problem Three versions of the problem (easiest to hardest) Algorithmic • Seller knows the market well. Incentive Compatible Auction • Customers submit lists / valuations to mechanism, which decides who gets what for how much. Must be in customers’ interest (dominant strategy) to report truthfully. Online Pricing • Customers arrive one at a time, buy what they want at current prices. Seller modifies prices over time. Maria-Florina Balcan

Algorithmic Problem, Single-minded Bidders • n item types (coffee, cups, sugar, apples), with unlimited supply of each. • m customers. • Each customer i has a shopping list Li and will only shop if the total cost of items in Li is at most some amount wi (otherwise he will go elsewhere). • Say all marginal costs to you are 0 [revisit this in a bit], and you know all the (Li, wi) pairs. What prices on the items will make you the most money? • Easy if all Li are of size 1. • What happens if all Li are of size 2? Maria-Florina Balcan

Algorithmic Pricing, Single-minded Bidders • A multigraph G with values we on edges e. • Goal: assign prices on vertices pv¸ 0 to maximize total profit, where: 5 15 10 30 40 10 20 5 • APX hard [GHKKKM’ 05]. Maria-Florina Balcan

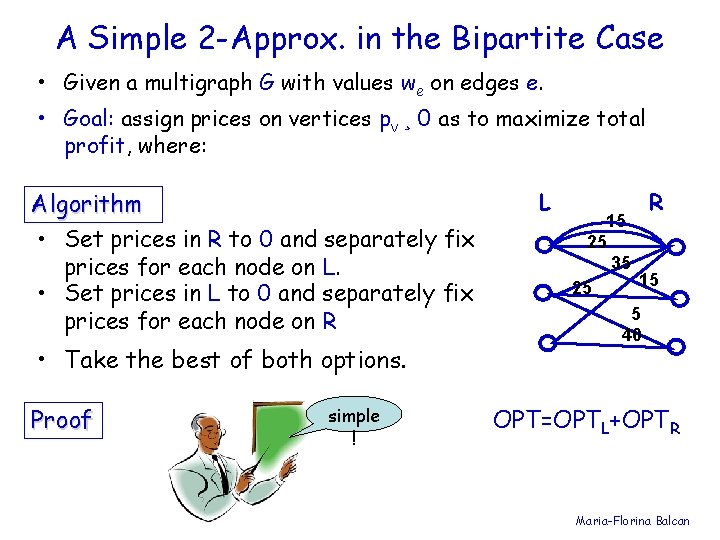
A Simple 2 -Approx. in the Bipartite Case • Given a multigraph G with values we on edges e. • Goal: assign prices on vertices pv ¸ 0 as to maximize total profit, where: Algorithm • Set prices in R to 0 and separately fix prices for each node on L. • Set prices in L to 0 and separately fix prices for each node on R • Take the best of both options. Proof simple ! L R 15 25 35 15 25 5 40 OPT=OPTL+OPTR Maria-Florina Balcan

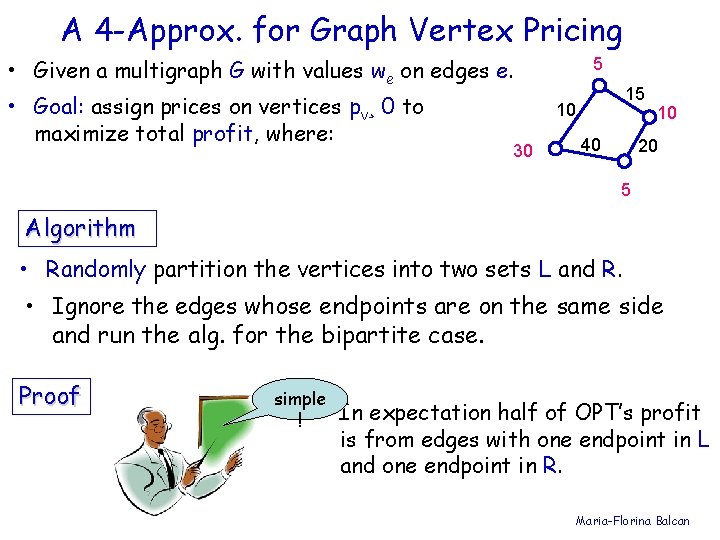
A 4 -Approx. for Graph Vertex Pricing • Given a multigraph G with values we on edges e. • Goal: assign prices on vertices pv¸ 0 to maximize total profit, where: 5 15 10 30 40 10 20 5 Algorithm • Randomly partition the vertices into two sets L and R. • Ignore the edges whose endpoints are on the same side and run the alg. for the bipartite case. Proof simple ! In expectation half of OPT’s profit is from edges with one endpoint in L and one endpoint in R. Maria-Florina Balcan

Algorithmic Pricing, Single-minded Bidders, k-hypergraph Problem What about lists of size · k? Algorithm 15 10 20 – Put each node in L with probability 1/k, in R with probability 1 – 1/k. – Let GOOD = set of edges with exactly one endpoint in L. Set prices in R to 0 and optimize L wrt GOOD. • Let OPTj, e be revenue OPT makes selling item j to customer e. Let Xj, e be indicator RV for j 2 L & e 2 GOOD. • Our expected profit at least: Maria-Florina Balcan

Algorithmic Pricing, Single-minded Bidders • What if items have constant marginal cost to us? • We can subtract these from each edge (view edge as amount willing to pay above our cost). 5 2 10 • Reduce to previous problem. 3 3 15 40 32 7 20 8 5 But, one difference: • Can now imagine selling some items below cost in order to make more profit overall. Maria-Florina Balcan

Algorithmic Pricing, Single-minded Bidders What if items have constant marginal cost to us? • We can subtract these from each edge (view edge as amount willing to pay above our cost). • Reduce to previous problem. But, one difference: • Can now imagine selling some items below cost in order to make more profit overall. 2 1 4 1 2 8 4 1 0 4 2 4 8 2 4 4 1 0 • Previous results only give good approximation wrt best “non-money-losing” prices. • Can actually give a log(n) gap between the two benchmarks. Maria-Florina Balcan

Algorithmic Problem, Single-minded Bidders Summary: • 4 approx for graph case. • O(k) approx for k-hypergraph case. Improves the O(k 2) approximation of Briest and Krysta, SODA’ 06. Coming up! – Also simpler and can be naturally adapted to the online setting. • Can de-randomize algorithms if desired. Other known results: • General O(log mn) approx. by picking the best single price [GHKKKM 05]. • (log n) hardness for general case [DFHS 06]. Maria-Florina Balcan

Incentive Compatible Auction Problem Same setup, but we don’t know lists or valuations. Goal: incentive compatible auction. • Customers submit valuation information. • Auction mechanism determines who buys what for how much. • Must be in customers’ self-interest to submit their true valuations. Maria-Florina Balcan

Incentive Compatible Auction Problem Generic randomized reductions to alg problem [BBHM’ 05]. E. g. : Basic Reduction: Random Sampling Auction • Bidders submit bids. • Randomly split the bidders into S 1 and S 2. • Run A on Si to get (nearly optimal) gi 2 G w. r. t. Si. • Apply g 1 over S 2 and g 2 over S 1 S g 1=OPT(S 1) g 2=OPT(S 2) S 2 Maria-Florina Balcan

Incentive Compatible Auction Problem Basic Reduction: Random Sampling Auction • Bidders submit bids. • Randomly split the bidders into S 1 and S 2. • Run A on Si to get (nearly optimal) gi 2 G w. r. t. Si. • Apply g 1 over S 2 and g 2 over S 1. Example Guarantee: If all valuations are between 1 and h, then Õ(hn/ 2) bidders are sufficient so that whp this loses only factor of (1+ ) in revenue. Maria-Florina Balcan

On-line Pricing Customers arrive one at a time, buy or don’t buy at current prices. In (full information) auction model, we know valuation info for customers 1, …, i-1 when customer i arrives. In posted-price model, only know who bought what for how much. Goal - do well compared to best fixed set of item prices. Maria-Florina Balcan

On-line Pricing Our O(k)-approx. alg. can be naturally adapted to the online setting, by using results of [BH’ 05] and [BKRW’ 03] for the online digital good auction. Can run separate online auctions over items in L, customers in GOOD (customers who want exactly one item in L). Guarantee: perform comparably to best fixed set of item prices (for pts in L, people in GOOD). Let OPTi be the best profit achievable (from item i) using a fixed price for item i from customers in GOOD whose bundle contain item i. Can use [BH’ 05] auction -- the expected profit of the online auction for item i is Maria-Florina Balcan

On-line Pricing Can run separate online auctions over items in L, customers in GOOD (customers that who want exactly one item in L). Let OPTi be the best profit achievable (from item i) using a fixed price for item i from customers in GOOD whose bundle contain item i. Using the [BH’ 05] auction, the expected profit of the online auction for item i is: Overall, we achieve profit at least: Profit of the offline approx. alg. Maria-Florina Balcan

Conclusions and Open Questions • Simple randomized alg achieving factor 4 for graphvertex pricing problem. • Factor O(k) for k-hypergraph vertex pricing. • Can then use generic technique to apply in auction setting. Use online learning methods to apply in online setting. Open Problems • 4 - , o(k). • How well can you do if pricing below cost is allowed? Maria-Florina Balcan