Approximating Edit Distance in NearLinear Time Alexandr Andoni

Approximating Edit Distance in Near-Linear Time Alexandr Andoni (MIT) Joint work with Krzysztof Onak (MIT)

Edit Distance two strings x, y ∑n l ed(x, y) = minimum number of edit operations to transform x into y l For ¡ Edit operations = insertion/deletion/substitution Example: ED(0101010, 1010101) = 2 l Important in: computational biology, text processing, etc

Computing Edit Distance l Problem: compute ed(x, y) for given x, y {0, 1}n l Exactly: ¡ ¡ l Approximately in n 1+o(1) time: ¡ l O(n 2) [Levenshtein’ 65] O(n 2/log 2 n) for |∑|=O(1) [Masek-Paterson’ 80] n 1/3+o(1) approximation [Batu-Ergun-Sahinalp’ 06], improving over [Sahinalp-Vishkin’ 96, Cole-Hariharan’ 02, Bar. Yossef. Jayram-Krauthgamer-Kumar’ 04] Sublinear time: ¡ ≤n 1 -ε vs ≥n/100 in n 1 -2ε time [Batu-Ergun-Kilian-Magen. Raskhodnikova-Rubinfeld-Sami’ 03]

Computing via embedding into ℓ 1 l Embedding: f: {0, 1}n → ℓ 1 ¡ such that ed(x, y) ≈ ||f(x) - f(y)||1 ¡ up to some distortion (=approximation) ¡ Can compute ed(x, y) in time to compute f(x) l Best embedding by [Ostrovsky-Rabani’ 05]: ¡ distortion = 2 O (√log n) ¡ Computation time: ~n 2 randomized (and similar dimension) ¡ Helps for nearest neighbor search, sketching, but not computation…

Our result l Theorem: Can compute ed(x, y) in ¡ n*2 O (√log n) time with ¡ 2 O (√log n) approximation l While uses some ideas of [OR’ 05] embedding, it is not an algorithm for computing the [OR’ 05] embedding

Review of Ostrovsky-Rabani embedding φm = embedding of strings of length m l δ(m) = distortion of φm l Embedding is recursive l ¡ ¡ Partition into b blocks (b later chosen to be exp(√log m)) Use embeddings φk for k ≤ m/b X= m/b l Embed each block separately as follows…

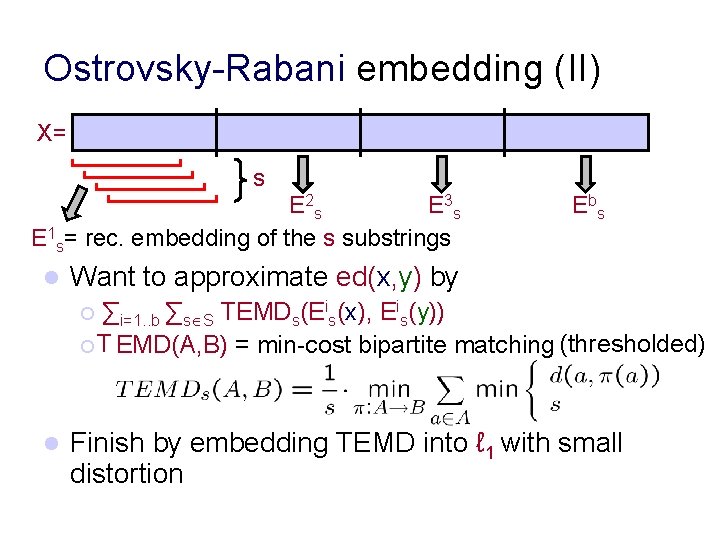
Ostrovsky-Rabani embedding (II) X= s E 2 s E 3 s E 1 s= rec. embedding of the s substrings l E bs Want to approximate ed(x, y) by ∑i=1. . b ∑s S TEMDs(Eis(x), Eis(y)) ¡ T EMD(A, B) = min-cost bipartite matching (thresholded) ¡ l Finish by embedding TEMD into ℓ 1 with small distortion

Distortion of [OR] embedding l Suppose can embed TEMD into ℓ 1 with distortion (log m)O(1) l Then [Ostrovsky-Rabani’ 05] show that distortion of φm is ¡ δ(m) l For ≤ (log m)O(1) * [δ(m/b) + b] b=exp[√log m] ¡ δ(m) ≤ exp[O (√log m)]

Why it is expensive to compute [OR] embedding X= s E 1 s= rec. embedding of the s substrings l In first step, need to compute recursive embedding for ~n/b strings of length ~n/b l The dimension blows up

Our Algorithm i x y z= z[i: i+m] l For each length m in some fixed set L [n], compute vectors vim ℓ 1 such that ||vim – vjm||1 ≈ ed( z[i: i+m], z[j: j+m] ) ¡ up to distortion δ(m) ¡ Dimension of vim is only O(log 2 n) Vectors vim are computed inductively from vik for k≤m/b (k L) l Output: ed(x, y)≈||v 1 n/2 – vn/2+1 n/2||1 (i. e. , for m=n/2=|x|=|y|) l l

Idea: intuition ||vim – vjm||1 ≈ ed( z[i: i+m], z[j: j+m] ) l For each m L, compute φm(z[i: i+m]) ¡ ¡ l as in the O-R recursive step except we use vectors vik, k<m/b & k L, in place of recursive embeddings of shorter substrings (sets Eis) Resulting φm(z[i: i+m]) have high dimension, >m/b… Use Bourgain’s Lemma to vectors φm(z[i: i+m]), i=1. . n-m, ¡ ¡ ¡ [Bourgain]: given n vectors qi, construct n vectors q i of O(log 2 n) dimension such that ||qi-qj||1 ≈ ||q i-q j||1 up to O(log n) distortion. Apply to vectors φm(z[i: i+m]) to obtain vectors vim of polylogaritmic dimension incurs O(log n) distortion at each step of recursion. but OK as there are only ~√log n steps, giving an additional distortion of only exp[O (√log n)]

Idea: implementation l Essential step is: l Main Lemma: fix n vectors vi ℓ 1, of dimension p=O(log 2 n). ¡ Let s<n. Define Ai={vi, vi+1, …, vi+s-1}. ¡ Then we can compute vectors qi ℓ 1 k for k=O(log 2 n) such that l ||qi – qj||1≈ TEMD(Ai, Aj) up to distortion log. O(1) n ¡ Computing qi’s takes O (n) time.

Proof of Main Lemma TEMD over n sets Ai O(log 2 n) minlow ℓ 1 high O(1) minlow ℓ 1 low O(log n) minlow tree-metric O(log 3 n) sparse graph-metric [Bourgain] (efficient) O(log n) ℓ 1 low l Graph-metric: shortest path on a weighted graph l Sparse: O (n) edges l “low” = log. O(1) n l mink M is semi-metric on Mk with “distance” dmin, M(x, y)=mini=1. . kd. M(xi, yi)

Step 1 TEMD over n sets Ai O(log 2 n) minlow ℓ 1 high Lemma 1: can embed TEMD over n sets in ({0. . M}p, ℓ 1) into min. O(log n) ℓ 1 M^p with O(log 2 n) distortion, w. h. p. l Use [A-Indyk-Krauthgamer’ 08] l ¡ l Embedding: for each Δ = powers of 2 ¡ ¡ l impose a randomly-shifted grid one coordinate per cell, equal to # of points in the cell Theorem [AIK]: ¡ ¡ l (similar to Ostrovsky-Rabani embedding) no contraction w. h. p. expected expansion = O(log 2 n) Just repeat O(log n) times

Step 2 minlow ℓ 1 high O(1) minlow ℓ 1 low Lemma 2: can embed an n point set from ℓ 1 M into min. O(log n) ℓ 1 k, for k=O(log 3 n), with O(1) distortion. l Use (weak) dimensionality reduction in ℓ 1 l Thm [Indyk’ 06]: Let A be matrix of size M by k=O(log 3 n) with each element chosen from Cauchy distribution. Then for any x =Ax, y =Ay: l no contraction: ||x -y ||1≥||x-y||1 (w. h. p. ) ¡ 5 -expansion: ||x -y ||1≤ 5*||x-y||1 (with 0. 01 probability) ¡ l Just use O(log n) of such embeddings

Efficiency of Step 1+2 l From step 1+2, we get some embedding f() of sets Ai={vi, vi+1, …, vi+s-1} into minlow ℓ 1 low l Naively would take Ω(n*s)=Ω(n 2) time to compute all f(Ai) l More efficiently: ¡ Note that f() is linear: f(A) = ∑a A f(a) ¡ Then f(Ai) = f(Ai-1)-f(vi-1)+f(vi+s-1) ¡ Compute f(Ai) in order, for a total of O (n) time

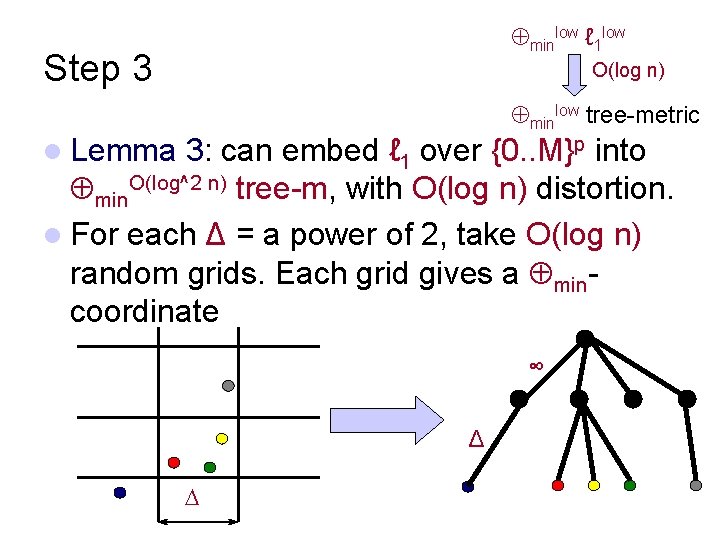
minlow ℓ 1 low Step 3 O(log n) minlow tree-metric l Lemma 3: can embed ℓ 1 over {0. . M}p into min. O(log^2 n) tree-m, with O(log n) distortion. l For each Δ = a power of 2, take O(log n) random grids. Each grid gives a mincoordinate ∞ Δ

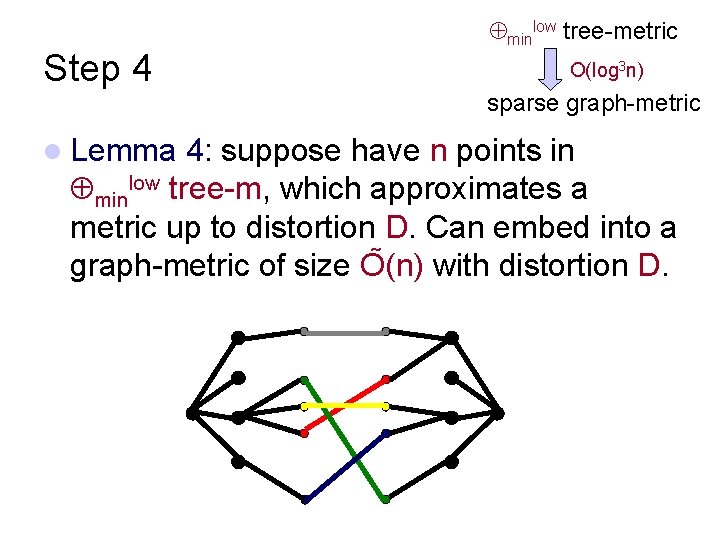
Step 4 minlow tree-metric O(log 3 n) sparse graph-metric l Lemma 4: suppose have n points in minlow tree-m, which approximates a metric up to distortion D. Can embed into a graph-metric of size O (n) with distortion D.

Step 5 sparse graph-metric O(log n) ℓ 1 low l Lemma 5: Given a graph with m edges, can embed the graph-metric into ℓ 1 low with O(log n) distortion in O (m) time. l Just implement Bourgain’s embedding: ¡ Choose O(log 2 n) sets Bi ¡ Need to compute the distance from each node to each Bi ¡ For each Bi can compute its distance to each node using Dijkstra’s algorithm in O (m) time

Summary of Main Lemma TEMD over n sets Ai O(log 2 n) minlow ℓ 1 high O(1) oblivious minlow ℓ 1 low O(log n) min low tree-metric O(log 3 n) sparse graph-metric non-oblivious O(log n) ℓ 1 low l Min-product helps to get low dimension (~small-size sketch) ¡ bypasses impossibility of dim-reduction in ℓ 1 l Ok that it is not a metric, as long as it is close to a metric

Conclusion + a question l Theorem: can compute ed(x, y) in n*2 O (√log n) time with 2 O (√log n) approximation l Question: can we do the following “oblivious” dimensionality reduction in ℓ 1 ¡ ¡ Given n, construct a randomized embedding φ: ℓ 1 M→ℓ 1 polylog n such that for any v 1…vn ℓ 1 M, with high probability, φ has distortion log. O(1) n on these vectors? If φ exists, it cannot be linear [Charikar-Sahai’ 02]