Approximate String Matching Alignment with gaps Global alignment

Approximate String Matching Alignment with gaps

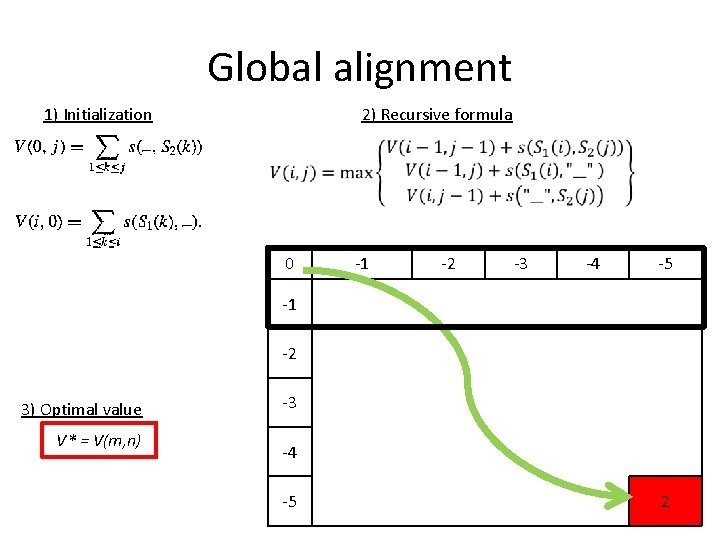
Global alignment 1) Initialization 2) Recursive formula 0 -1 -2 -3 -4 -5 -1 -2 3) Optimal value V* = V(m, n) -3 -4 -5 2

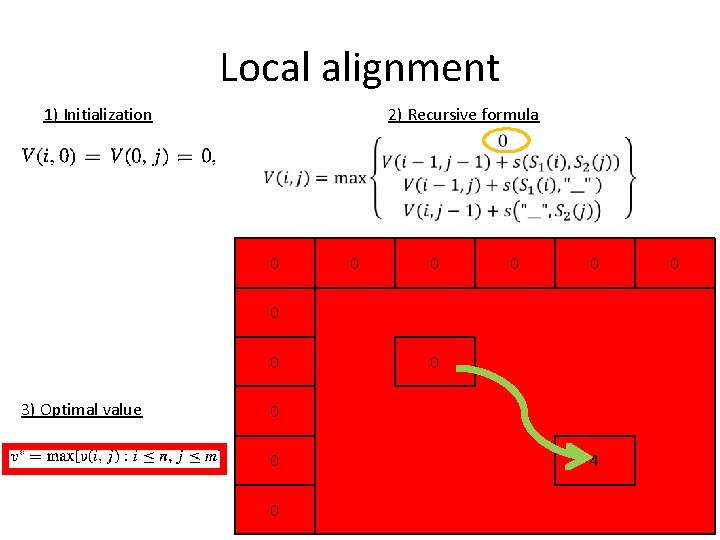
Local alignment 1) Initialization 2) Recursive formula 0 0 0 0 3) Optimal value 0 0 4 0

Problem 1 •

Solution 1. Run the algorithm for optimal local alignment with the 2 -rows method and save the value v*. Running-time: O(nm) Space: O(n+m) 2. Run the algorithm again using the q-rows method. Each time when V(i, j)=v*, try building the optimal alignment by back-tracing the green pointers in q rows and report if succeeded. Running-time: O(mn + rq) Space: O( q min(n, m) )

Solution: use a q-rows method 0 0 0 0 2 2 1 2 0 0 3 3 2 4 3 0 1 2 2 3 4 2 0 0 q

Problem 2 Assume that we know that there exists an optimal local alignment of the two substrings of length at most q << |S 1|, |S 2|. Find an optimal local alignment between S 1 and S 2, using • space O(|S 1|+|S 2|+ r +q 2) • time O(|S 1|*|S 2|+r q 2), where r is the number of distinct pairs of end-indexes of optimal local alignments

Solution 1) Run the algorithm with the two-rows method, to find V* and the list of all r pairs (i, j) such Running-time: O(nm) that V(i, j) = V*. Space: O(n+m+r) 2) For each pair (i, j) in the list, compute the local optimal alignment on the table of S 1[i-q+1 … i] and S 2[j-q+1 … j]. If the optimal value is V* , restore and report that alignment. Running-time: O(rq 2) Space: O(r+q 2)

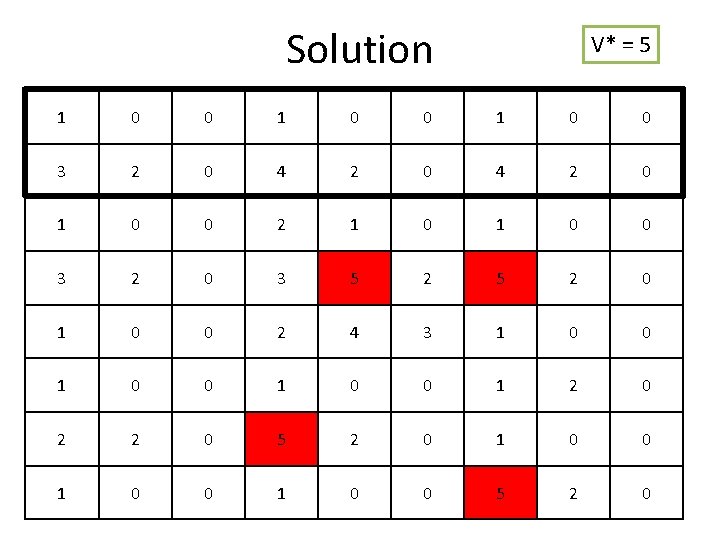
Solution V* = 5 1 0 0 3 2 0 4 2 0 1 0 0 2 1 0 0 3 2 0 3 5 2 0 1 0 0 2 4 3 1 0 0 1 2 0 2 2 0 5 2 0 1 0 0 5 2 0

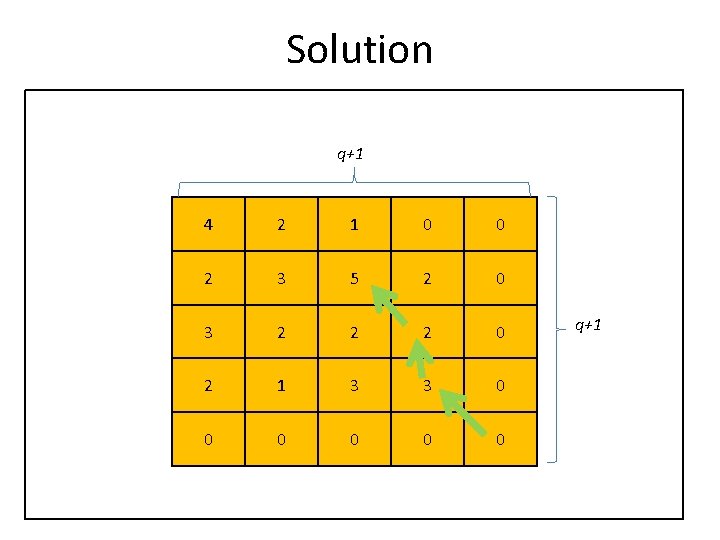
Solution q+1 4 2 1 0 0 2 3 5 2 0 3 2 2 2 0 2 1 3 3 0 0 0 q+1

Alignments with gaps We are given cost-function w(k) (creating a gap of size k costs w(k) ) What is the running-time?

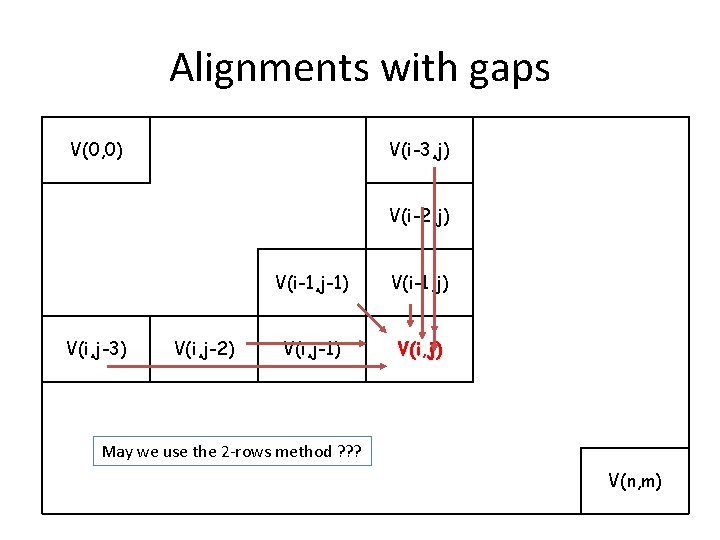
Alignments with gaps V(0, 0) V(i-3, j) V(i-2, j) V(i, j-3) V(i, j-2) V(i-1, j-1) V(i-1, j) V(i, j-1) V(i, j) May we use the 2 -rows method ? ? ? V(n, m)

Gaps allowed on one string only V(0, 0) V(i-3, j) V(i-2, j) V(i-1, j-1) V(i-1, j) V(i, j-1) V(i, j) May we use the 2 -rows method ? ? ? V(n, m)

Consecutive gaps For some gap cost functions, the actual minimal penalty of creating a gap of length k might be composed of the scores of several consecutive shorter gaps

Affine gap cost function Price for starting a gap Price for each space in the gap What is the running-time? O(nm) General gap function