Approximate Integration The Trapezoidal Rule Claus Schubert May

Approximate Integration: The Trapezoidal Rule Claus Schubert May 25, 2000

Why Approximate Integration? z Can’t always find an antiderivative Example: z Don’t always know the function

First Approach: Riemann Sums z Use left or right Riemann sums to approximate the integral. z Left Riemann sum: Dx: length of the n subintervals xi: endpoints of the subintervals

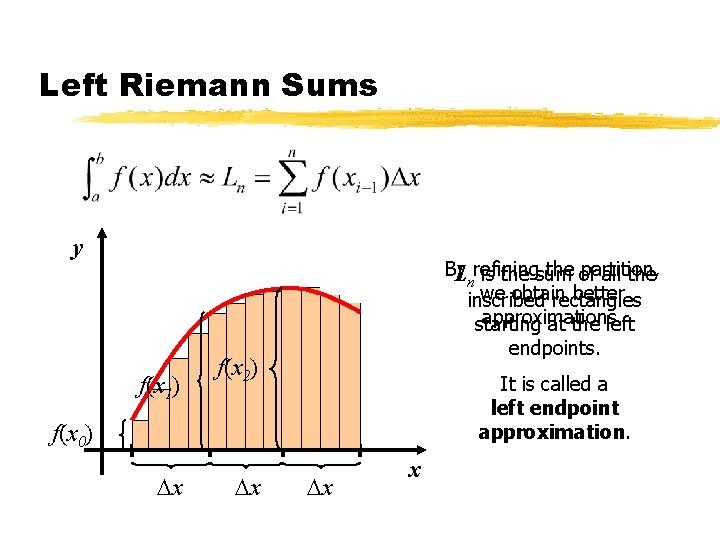
Left Riemann Sums y By the of partition, Lnrefining is the sum all the we obtain better inscribed rectangles approximations. starting at the left f(x 1) endpoints. f(x 2) It is called a left endpoint approximation. f(x 0) x 0 Dx x 1 Dx x 2 Dx x 3 x

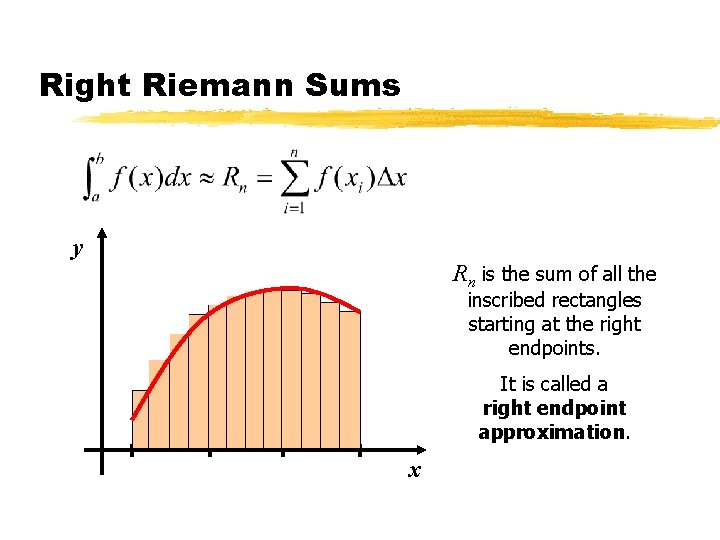
Right Riemann Sums y Rn is the sum of all the inscribed rectangles starting at the right endpoints. It is called a right endpoint approximation. x 0 x 1 x 2 x 3 x

Left and Right Endpoint Approximations z Observations: y Approximations get better if we increase n y If Ln underestimates, then Rn overestimates, and vice versa z Idea for improvement: y Take the average of both approximations

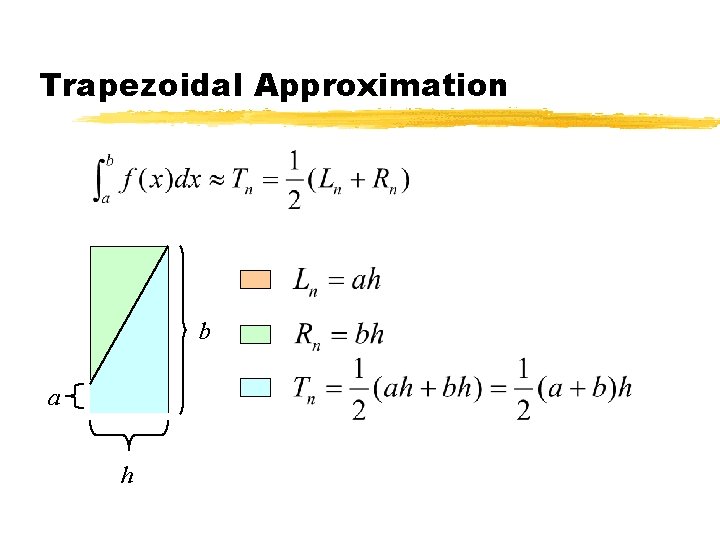
Trapezoidal Approximation b a h

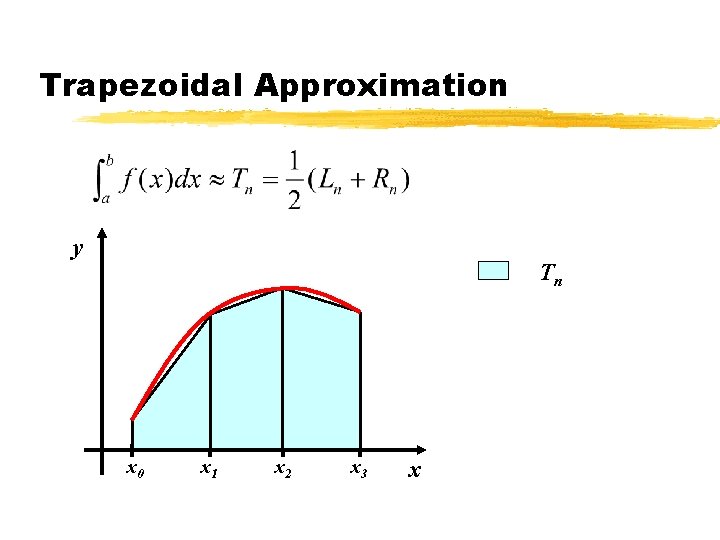
Trapezoidal Approximation y Lnn T Rn x 0 x 1 x 2 x 3 x

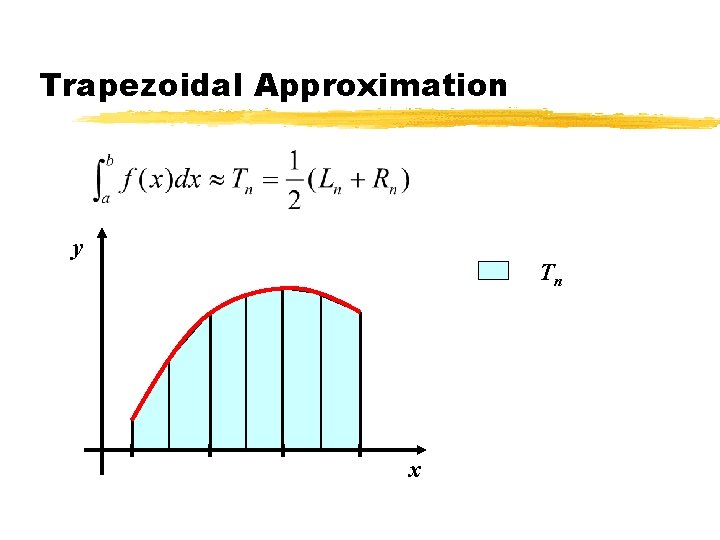
Trapezoidal Approximation y Tn x 0 x 1 x 2 x 3 x

Trapezoidal Approximation

An Example As an example, let us look at .

An Example

Error bounds z Question: How accurate is the trapezoidal approximation? z Answer: where K is an upper bound for | f”(x) |.

Error bounds: An Example In our previous example, how large should n be so that the error is less than 0. 00001 ?

Error bounds: An Example

Let’s Wrap Up z Approximations are useful if the function cannot be integrated or no function is given to begin with. z Left and right endpoint approximations are too inaccurate, so take their average. z The trapezoidal approximation is much more accurate than the left/right approximations, but better approximations exist (midpoint, Simpson’s etc. ) z You need a computer to find approximations with large n - or you need to get a life!!!