Approximate Dynamic Programming for HighDimensional Resource Allocation Problems

Approximate Dynamic Programming for High-Dimensional Resource Allocation Problems Princeton University, Warren B. Powell Long-Term PAYOFF: Efficient, robust control of complex systems of people, equipment and resources. Advances in fundamental algorithms for stochastic control with many applications. OBJECTIVES • Fast algorithms for real-time control. • Optimal learning rates to maximize rate of convergence and adapt to new conditions. • Self-adapting planning models which minimize tuning and calibration. • Robust solutions which improve response to random events. APPROACH/TECHNICAL CHALLENGES FUNDING ($K)—Show all funding contributing to this project • Approximate dynamic programming combining math programming, signal processing and recursive statistics. FY 05 FY 06 FY 07 FY 08 FY 09 AFOSR Funds 190 197 205 Several industrial sponsors who provide applications for ADP in different settings. Additional funds from NSF, Canadian Air Force. • Challenge: quickly finding stable policies in the presence of high-dimensional state variables. TRANSITIONS • Adoption by several industrial sponsors. • 9 publications (inc. 4 to appear) in 2006. • Interaction with AFRL (summer, 2006) and ongoing relationship with AMC (tanker refueling) ACCOMPLISHMENTS/RESULTS · New method for optimal learning (the “knowledge gradient”). · Reduced solution time for a class of nonlinear control problems from hours to seconds. STUDENTS, POST-DOCS · Adaptation to robust response of spare parts, 3 students, 1 post-doc transportation control, general resource allocation.

Technical approach • Approximate dynamic programming for high-dimensional resource allocation problems Standard formulation of Bellman’s equation: Steps in ADP strategy: Simulate (from post to pre-decision state) State variables with 10 dimensions can produce state spaces with 100 million elements. Real problems exhibit state vectors with millions of dimensions. Solve deterministic optimization problem: Statistically update value function approx: Technical advances in 2006: Ø New optimal stepsize algorithm accelerates recursive learning (extends Kalman filter to nonstationary dataset – publication has appeared in Machine Learning). Ø New hierarchical learning algorithm estimates variable-dimensioned approximation, adapting to higher-dimensional representation as algorithm progresses. Avoids need to prespecify a particular functional form. Ø Convergence proofs for special problem classes which do not require state space exploration (which do not work for high dimensional problems).

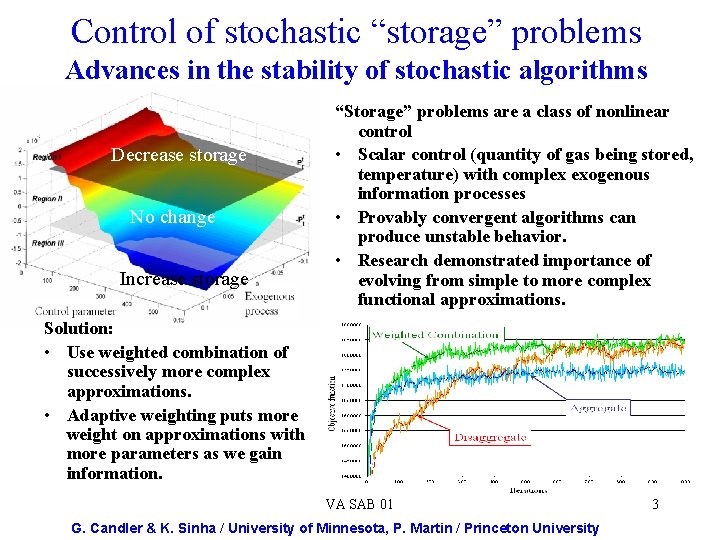
Control of stochastic “storage” problems Advances in the stability of stochastic algorithms Decrease storage No change Increase storage “Storage” problems are a class of nonlinear control • Scalar control (quantity of gas being stored, temperature) with complex exogenous information processes • Provably convergent algorithms can produce unstable behavior. • Research demonstrated importance of evolving from simple to more complex functional approximations. Solution: • Use weighted combination of successively more complex approximations. • Adaptive weighting puts more weight on approximations with more parameters as we gain information. VA SAB 01 G. Candler & K. Sinha / University of Minnesota, P. Martin / Princeton University 3

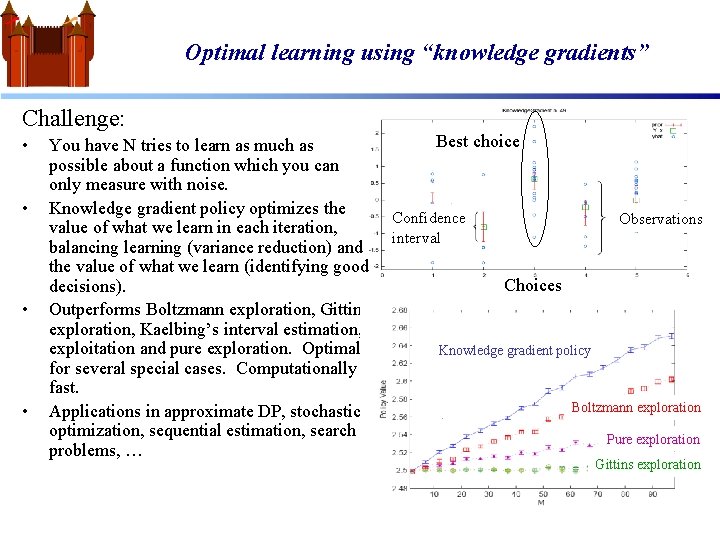
Optimal learning using “knowledge gradients” Challenge: • • You have N tries to learn as much as possible about a function which you can only measure with noise. Knowledge gradient policy optimizes the value of what we learn in each iteration, balancing learning (variance reduction) and the value of what we learn (identifying good decisions). Outperforms Boltzmann exploration, Gittins exploration, Kaelbing’s interval estimation, exploitation and pure exploration. Optimal for several special cases. Computationally fast. Applications in approximate DP, stochastic optimization, sequential estimation, search problems, … Best choice Confidence interval Observations Choices Knowledge gradient policy Boltzmann exploration Pure exploration Gittins exploration

Transitions • Managing locomotives at Norfolk Southern Railroad » Using AFOSR-sponsored research, modified ADP algorithm to use nested nonlinear value function approximations. Dramatic improvement in rate of convergence and stability of solution. » • Planning driver operations at Schneider National » ADP algorithm is planning movements of 7, 000 drivers with complex operational strategies. Used by Schneider full time to plan driver management policies. » • Fleet simulations for Netjets » » » Captures pilots, aircraft and requirements (customers); full work rules and operational constraints. After three years, model was judged to be calibrated in 2006. First study used to evaluate the effect of aircraft reliability. • Mid-air refueling simulator for AMC » » Optimized scheduling of tankers under uncertainty. Reduced required number of tankers by 20 percent over current planning methods.