Apprentissage spectral Spectral learning S D Kamvar D

Apprentissage spectral Spectral learning S. D. Kamvar, D. Klein, C. D. Manning IJCAI-03, 2003

Introduction n n Les algorithmes spectraux utilisent l'information contenue dans les vecteurs propres de la matrice d'affinité des données pour détecter des structures Applications : recherche d'information web, segmentation d'images, traitement de document, clustering, etc. Idée : développer des algorithmes spectraux pour l'apprentissage supervisé Adapter les méthodes "spectral clustering" à la classification (supervisée) n

Algorithmes de spectral clustering n n n Matrice d'affinité et Matrice de transition de Markov (probabilités) Pour 2 points xi et xj on associe la distance d(xi, xj). On définit la matrice d'affinité A par : est un paramètre libre Les méthodes spectrales utilisent différentes normalisations : Algorithme Normalisation Formule MNCUT Asymétrie N = D-1 A NJW Symétrie N = D-1/2 AD-1/2 LSA* Rien N=A SL Normalisée N = (A + dmax. I – D)/dmax *Latent Semantic Analysis • D = diag{Dii} avec : • dmax = max(Dii)

Sélection du paramètre libre sigma n L'importance de la sélection du paramètre sigma est souvent négligée (L'auteur renvoie à NJW On spectral clustering: Analysis and an algorithm, NIPS 14, 2002) : K plus proches voisins distance moyenne plage de stabilité des résultats, etc.

Algorithme d'apprentissage spectral n Représentation spectrale ¨ ¨ ¨ n Former la matrice d'affinité Définir la matrice degré D Normaliser N = (A + dmax. I – D)/dmax Chercher les k plus grands vecteurs propres : x 1, . . . , xk pour former la matrice X RNxk Normaliser X pour avoir les lignes de module 1 Clustering Traiter chaque colonne comme un point dans Rk. Classer dans l'espace spectral en k classes par k-means ou autre algorithme ¨ Affecter les points d'origine i à la classe j SSI la ième colonne de X a été affectée à la classe j ¨ n Classification Représenter chaque point i par sa colonne Xi de X ¨ Classer les colonnes comme points dans Rk par un classifieur supervisé avec labels ¨ Affecter chaque point i à la classe c à laquelle Xi a été affectée. ¨

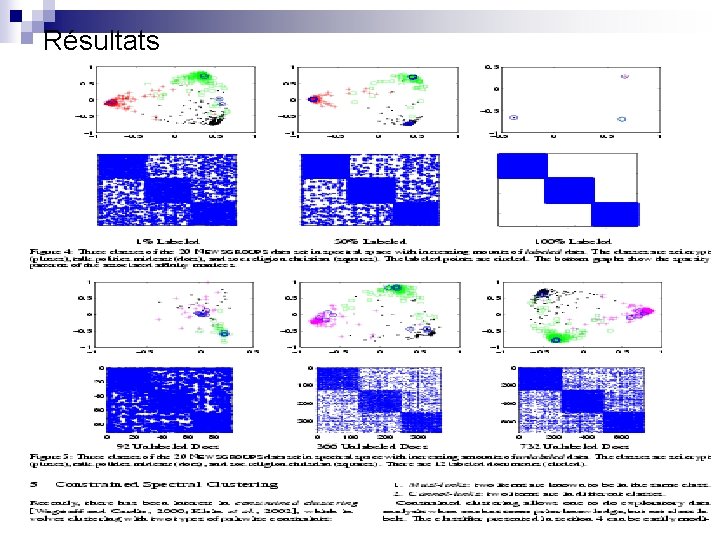
Classification spectrale n Comment intégrer les labels dans le graphe ? Les points non labellisés ont leurs poids % à leurs similarités donc leurs affinités comme en spectral clustering ¨ Pour chaque paire de points (i, j) qui sont issus de la même classe mettre : ¨ Aij = Aji = 1 Pour chaque paire de points (i, j) qui sont de classes différentes mettre : Aij = Aji = 0 ¨ Normaliser A : N = (A + dmax. I – D)/dmax ¨ n Lien avec Constrained Spectral Clustering : Les points sans labels ont leurs poids % à leurs similarités donc leurs affinités sont comme avant ¨ Must-links : 2 points de même classe (sans connaître le label) : Aij = Aji = 1 ¨ Cannot-links : 2 points de classes différentes : Aij = Aji = 0 ¨ Normaliser A : N = (A + dmax. I –D)/dmax ¨

Résultats