Applying the Quadratic Formula 1 Applying the Quadratic

Applying the Quadratic Formula 1 Applying the Quadratic Formula

Warm-Up 2 Applying the Quadratic Formula

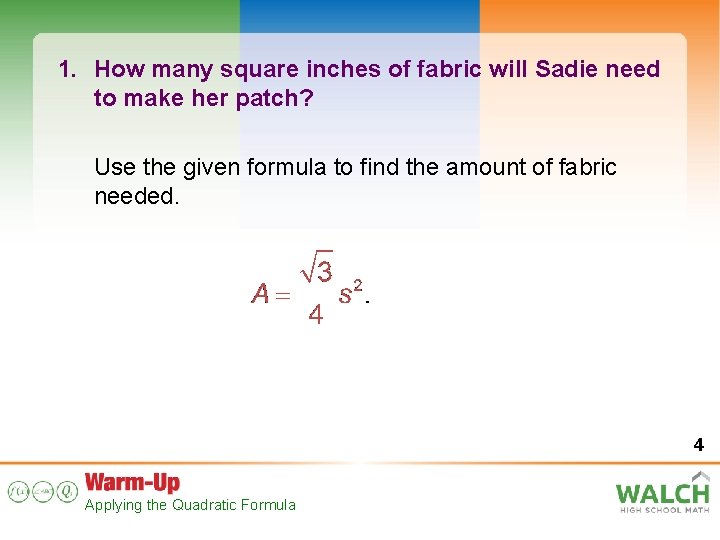
Sadie wants to sew a patch onto her shirt in the shape of an equilateral triangle with sides that are 4 inches long. The area of an equilateral triangle with sides of length s is given by 1. How many square inches of fabric will Sadie need to make her patch? 2. If Sadie decides to make 3 of her friends each a matching patch, how many square inches of fabric will Sadie need for the additional patches? Applying the Quadratic Formula 3

1. How many square inches of fabric will Sadie need to make her patch? Use the given formula to find the amount of fabric needed. 4 Applying the Quadratic Formula

Formula for the area of an equilateral triangle Substitute 4 for s. Simplify. The area of the triangular patch is or about 6. 93 square inches, 5 Applying the Quadratic Formula

2. If Sadie decides to make 3 of her friends each a matching patch, how many square inches of fabric will Sadie need for the additional patches? Multiply the amount of fabric needed for one patch by 3. The amount of fabric needed for the 3 additional patches is square inches, or about 20. 78 square inches. 6 Applying the Quadratic Formula

Instruction 7 Completing the Square

Introduction Completing the square can be a long process, and not all quadratic expressions can be factored. Rather than completing the square or factoring, we can use a formula that can be derived from the process of completing the square. This formula, called the quadratic formula, can be used to solve any quadratic equation. 8 Applying the Quadratic Formula

Key Concepts A quadratic equation when written in standard form, ax 2 + bx + c = 0, can be solved for x by using the quadratic formula: 9 Applying the Quadratic Formula

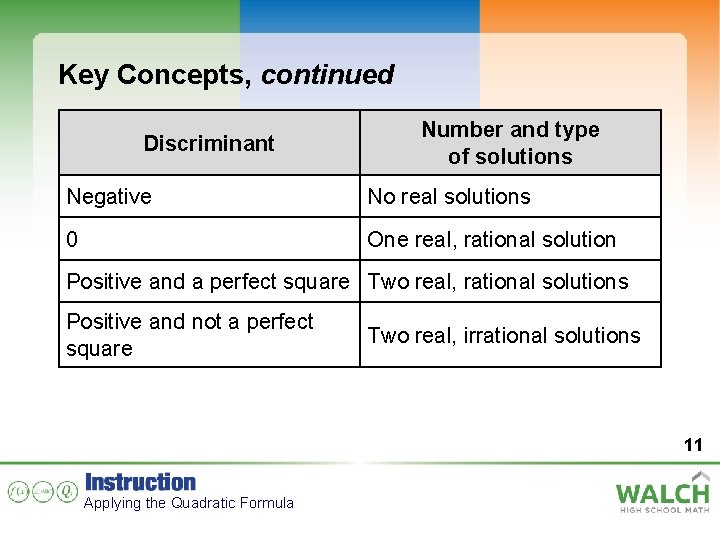
Key Concepts Solutions of quadratic equations are also called roots. The expression under the radical in the formula, – 4 ac, is called the discriminant. b 2 The discriminant tells us the number and type of solutions for the quadratic equation. 10 Applying the Quadratic Formula

Key Concepts, continued Discriminant Number and type of solutions Negative No real solutions 0 One real, rational solution Positive and a perfect square Two real, rational solutions Positive and not a perfect square Two real, irrational solutions 11 Applying the Quadratic Formula

Common Errors/Misconceptions • not setting the quadratic equation equal to 0 before determining the values of a, b, and c • forgetting to use ± when taking the square root to solve for x • writing the denominator of the quadratic formula as a instead of 2 a • not following the order of operations • not fully simplifying solutions 12 Applying the Quadratic Formula

Guided Practice Example 1 Given the standard form of a quadratic equation, ax 2 + bx + c = 0, derive the quadratic formula by completing the square. 13 Applying the Quadratic Formula

Guided Practice: Example 1, continued 1. Begin with a quadratic equation in standard form. ax 2 + bx + c = 0 14 Applying the Quadratic Formula

Guided Practice: Example 1, continued 2. Subtract c from both sides. ax 2 + bx + c = 0 ax 2 + bx = −c 15 Applying the Quadratic Formula

Guided Practice: Example 1, continued 3. Divide both sides by a. ax 2 + bx = −c 16 Applying the Quadratic Formula

Guided Practice: Example 1, continued 4. Complete the square. Add the square of one-half of the coefficient of the x-term to both sides to complete the square. Add to both sides of the equation to complete the square. 17 Applying the Quadratic Formula

Guided Practice: Example 1, continued 5. Write the left side of the equation as a binomial squared and simplify the right side of the equation. 18 Applying the Quadratic Formula

Guided Practice: Example 1, continued 6. Take the square root of both sides of the equation and simplify the right side. Previous equation: 19 Applying the Quadratic Formula

Guided Practice: Example 1, continued 7. Subtract from both sides of the equation to solve for x. Previous equation: 20 Applying the Quadratic Formula

Guided Practice: Example 1, continued 8. Combine the two fractions from the previous step. Previous equation: ✔ 21 Applying the Quadratic Formula

Guided Practice Example 2 Use the discriminant of 3 x 2 – 5 x + 1 = 0 to identify the number and type of solutions. 22 Applying the Quadratic Formula

Guided Practice: Example 2, continued 1. Determine a, b, and c. 3 x 2 – 5 x + 1 = 0 a=3 b = – 5 c=1 23 Applying the Quadratic Formula

Guided Practice: Example 2, continued 2. Substitute the values for a, b, and c into the formula for the discriminant, b 2 – 4 ac. a = 3, b = – 5, and c = 1 b 2 – 4 ac = (– 5)2 – 4(3)(1) = 25 – 12 = 13 The discriminant of 3 x 2 – 5 x + 1 = 0 is 13. 24 Applying the Quadratic Formula

Guided Practice: Example 2, continued 3. Use what you know about the discriminant to determine the number and type of solutions for the quadratic equation. The discriminant, 13, is positive, but it is not a perfect square. Therefore, there will be two real, irrational solutions. ✔ Applying the Quadratic Formula 25

Guided Practice: Example 2, continued 26 Applying the Quadratic Formula

Guided Practice Example 3 Solve 2 x 2 – 5 x = 12 using the quadratic formula. 27 Applying the Quadratic Formula

Guided Practice: Example 3, continued 1. Write the quadratic equation in standard form. 2 x 2 – 5 x = 12 Original equation 2 x 2 – 5 x – 12 = 0 Subtract 12 from both sides. 28 Applying the Quadratic Formula

Guided Practice: Example 3, continued 2. Determine the values of a, b, and c. 2 x 2 – 5 x – 12 = 0 a=2 b = – 5 c = – 12 29 Applying the Quadratic Formula

Guided Practice: Example 3, continued 3. Substitute the values of a, b, and c into the quadratic formula. a = 2, b = – 5, and c = – 12 Quadratic formula Substitute values for a, b, and c. Simplify. 30 Applying the Quadratic Formula

Guided Practice: Example 3, continued Simplify. 31 Applying the Quadratic Formula

Guided Practice: Example 3, continued 4. Determine the solution(s). Since the discriminant, 121, is positive and a perfect square, there are two real, rational solutions. Write the fraction from step 3 as two fractions and simplify. 32 Applying the Quadratic Formula

Guided Practice: Example 3, continued The solutions to the equation 2 x 2 – 5 x = 12 are x = 4 and ✔ 33 Applying the Quadratic Formula

Guided Practice: Example 3, continued 34 Applying the Quadratic Formula

Guided Practice Example 4 Solve x 2 = 2 x - 1 using the quadratic formula. 35 Applying the Quadratic Formula

Guided Practice: Example 4, continued 1. Write the quadratic equation in standard form. x 2 = 2 x – 1 Original equation x 2 – 2 x = -1 Subtract 2 x from both sides. x 2 - 2 x + 1 = 0 Add 1 to both sides. 36 Applying the Quadratic Formula

Guided Practice: Example 4, continued 2. Determine the values of a, b, and c. x 2 – 2 x + 1 = 0 a=1 b = – 2 c=1 37 Applying the Quadratic Formula

Guided Practice: Example 4, continued 3. Substitute the values of a, b, and c into the quadratic formula. a = 1, b = – 2, and c = 1 Quadratic formula Substitute values for a, b, and c. Simplify. 38 Applying the Quadratic Formula

Guided Practice: Example 4, continued Simplify. 39 Applying the Quadratic Formula

Guided Practice: Example 4, continued 4. Determine the solution(s). Since the discriminant is 0, there is one real, rational solution. ✔ The solution to the equation x 2 = 2 x - 1 is x = 1. 40 Applying the Quadratic Formula

Guided Practice Example 5 Solve 5 x 2 + 2 x + 3 = 0 using the quadratic formula. 41 Applying the Quadratic Formula

Guided Practice: Example 4, continued 1. The quadratic is already in standard form. Determine the values of a, b, and c. 5 x 2 + 2 x + 3 = 0 a=5 b=2 c=3 42 Applying the Quadratic Formula

Guided Practice: Example 4, continued 3. Substitute the values of a, b, and c into the quadratic formula. a = 5, b = 2, and c = 3 Quadratic formula Substitute values for a, b, and c. Simplify. 43 Applying the Quadratic Formula

Guided Practice: Example 4, continued Subtract the values under the radical sign. 44 Applying the Quadratic Formula

Guided Practice: Example 4, continued 3. Determine the solution(s). Since the discriminant is negative, the solutions will be complex. The solutions are and ✔ 45 Applying the Quadratic Formula