Applied Symbolic Computation CS 680480 Lecture 6 Multiplication

Applied Symbolic Computation (CS 680/480) Lecture 6: Multiplication, Interpolation, and the Chinese Remainder Theorem Jeremy R. Johnson May 9, 2001 Applied Symbolic Computation 1

Introduction • Objective: To derive a family of asymptotically fast integer multiplication algorithms using polynomial interpolation – – – – Karatsuba’s Algorithm Polynomial algebra Interpolation Vandermonde Matrices Toom-Cook algorithm Polynomial multiplication using interpolation Polynomial version of the Chinese Remainder Theorem References: Lipson, Cormen et al. May 9, 2001 Applied Symbolic Computation 2

Karatsuba’s Algorithm • Using the classical pen and paper algorithm two n digit integers can be multiplied in O(n 2) operations. Karatsuba came up with a faster algorithm. • Let A and B be two integers with – A = A 110 k + A 0, A 0 < 10 k – B = B 110 k + B 0, B 0 < 10 k – C = A*B = (A 110 k + A 0)(B 110 k + B 0) = A 1 B 1102 k + (A 1 B 0 + A 0 B 1)10 k + A 0 B 0 Instead this can be computed with 3 multiplications • T 0 = A 0 B 0 • T 1 = (A 1 + A 0)(B 1 + B 0) • T 2 = A 1 B 1 • C = T 2102 k + (T 1 - T 0 - T 2)10 k + T 0 May 9, 2001 Applied Symbolic Computation 3

Complexity of Karatsuba’s Algorithm • Let T(n) be the time to compute the product of two n-digit numbers using Karatsuba’s algorithm. Assume n = 2 k. T(n) = (nlg(3)), lg(3) 1. 58 • T(n) 3 T(n/2) + cn 3(3 T(n/4) + c(n/2)) + cn = 32 T(n/22) + cn(3/2 + 1) 32(3 T(n/23) + c(n/4)) + cn(3/2 + 1) = 33 T(n/23) + cn(32/22 + 3/2 + 1) … 3 i. T(n/2 i) + cn(3 i-1/2 i-1 + … + 3/2 + 1). . . cn[((3/2)k - 1)/(3/2 -1)] --- Assuming T(1) c 2 c(3 k - 2 k) 2 c 3 lg(n) = 2 cnlg(3) May 9, 2001 Applied Symbolic Computation 4

Divide & Conquer Recurrence Assume T(n) = a. T(n/b) + (n) • T(n) = (n) [a < b] • T(n) = (nlog(n)) [a = b] • T(n) = (nlogb(a)) May 9, 2001 [a > b] Applied Symbolic Computation 5

Polynomial Algebra • Let F[x] denote the set of polynomials in the variable x whose coefficients are in the field F. • F[x] becomes an algebra where +, * are defined by polynomial addition and multiplication. May 9, 2001 Applied Symbolic Computation 6

Interpolation • A polynomial of degree n is uniquely determined by its value at (n+1) distinct points. Theorem: Let A(x) and B(x) be polynomials of degree m. If A( i) = B( i) for i = 0, …, m, then A(x) = B(x). Proof. Recall that a polynomial of degree m has m roots. A(x) = Q(x)(x- ) + A( ), if A( ) = 0, A(x) = Q(x)(x- ), and deg(Q) = m-1 Consider the polynomial C(x) = A(x) - B(x). Since C( i) = A( i) B( i) = 0, for m+1 points, C(x) = 0, and A(x) must equal B(x). May 9, 2001 Applied Symbolic Computation 7

Lagrange Interpolation Formula • Find a polynomial of degree m given its value at (m+1) distinct points. Assume A( i) = yi • Observe that May 9, 2001 Applied Symbolic Computation 8

Matrix Version of Polynomial Evaluation • Let A(x) = a 3 x 3 + a 2 x 2 + a 1 x + a 0 • Evaluation at the points , , , is obtained from the following matrix-vector product May 9, 2001 Applied Symbolic Computation 9

Matrix Interpretation of Interpolation • Let A(x) = anxn + … + a 1 x +a 0 be a polynomial of degree n. The problem of determining the (n+1) coefficients an, …, a 1, a 0 from the (n+1) values A( 0), …, A( n) is equivalent to solving the linear system May 9, 2001 Applied Symbolic Computation 10

Vandermonde Matrix V( 0, …, n) is non-singular when 0, …, n are distinct. May 9, 2001 Applied Symbolic Computation 11

Polynomial Multiplication using Interpolation • Compute C(x) = A(x)B(x), where degree(A(x)) = m, and degree(B(x)) = n. Degree(C(x)) = m+n, and C(x) is uniquely determined by its value at m+n+1 distinct points. • [Evaluation] Compute A( i) and B( i) for distinct i, i=0, …, m+n. • [Pointwise Product] Compute C( i) = A( i)*B( i) for i=0, …, m+n. • [Interpolation] Compute the coefficients of C(x) = cnxm+n + … + c 1 x +c 0 from the points C( i) = A( i)*B( i) for i=0, …, m+n. May 9, 2001 Applied Symbolic Computation 12

Interpolation and Karatsuba’s Algorithm • Let A(x) = A 1 x + A 0, B(x) = B 1 x + B, C(x) = A(x)B(x) = C 2 x 2 + C 1 x + C 0 • Then A(10 k) = A, B(10 k) = B, and C = C(10 k) = A(10 k)B(10 k) = AB • Use interpolation based algorithm: – – Evaluate A( ), A( ) and B( ), B( ) for = 0, = 1, and =. Compute C( ) = A( )B( ), C( ) = A( )B( ) Interpolate the coefficients C 2, C 1, and C 0 Compute C = C 2102 k + C 110 k + C 0 May 9, 2001 Applied Symbolic Computation 13

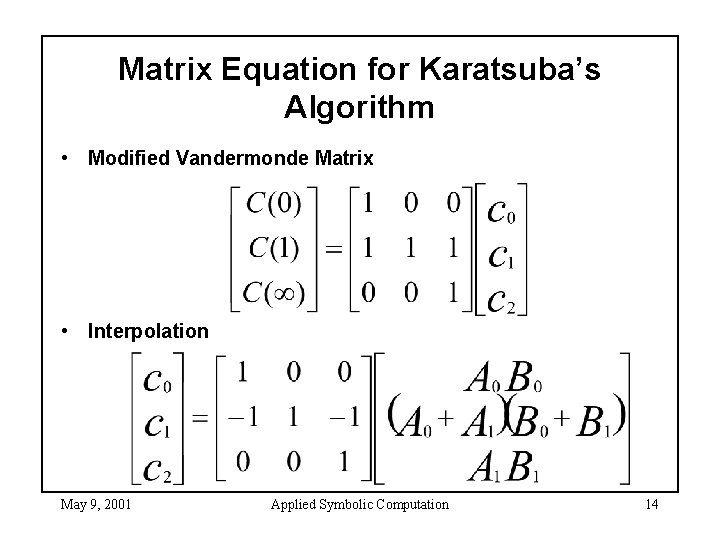
Matrix Equation for Karatsuba’s Algorithm • Modified Vandermonde Matrix • Interpolation May 9, 2001 Applied Symbolic Computation 14

Integer Multiplication Splitting the Inputs into 3 Parts • Instead of breaking up the inputs into 2 equal parts as is done for Karatsuba’s algorithm, we can split the inputs into three equal parts. • This algorithm is based on an interpolation based polynomial product of two quadratic polynomials. • Let A(x) = A 2 x 2 + A 1 x + A 0, B(x) = B 2 x 2 + B 1 x + B, C(x) = A(x)B(x) = C 4 x 4 + C 3 x 3 + C 2 x 2 + C 1 x + C 0 • Thus there are 5 products. The divide and conquer part still takes time = O(n). Therefore the total computing time T(n) = 5 T(n/3) + O(n) = (nlog 3(5)), log 3(5) 1. 46 May 9, 2001 Applied Symbolic Computation 15

Asymptotically Fast Integer Multiplication • We can obtain a sequence of asymptotically faster multiplication algorithms by splitting the inputs into more and more pieces. • If we split A and B into k equal parts, then the corresponding multiplication algorithm is obtained from an interpolation based polynomial multiplication algorithm of two degree (k-1) polynomials. • Since the product polynomial is of degree 2(k-1), we need to evaluate at 2 k-1 points. Thus there are (2 k-1) products. The divide and conquer part still takes time = O(n). Therefore the total computing time T(n) = (2 k-1)T(n/k) + O(n) = (nlogk(2 k-1)). May 9, 2001 Applied Symbolic Computation 16

Asymptotically Fast Integer Multiplication • Using the previous construction we can find an algorithm to multiply two n digit integers in time (n 1+ ) for any positive . – logk(2 k-1) = logk(k(2 -1/k)) = 1 + logk(2 -1/k) – logk(2 -1/k) logk(2) = ln(2)/ln(k) 0. • Can we do better? • The answer is yes. There is a faster algorithm, with computing time (nlog(n)loglog(n)), based on the fast Fourier transform (FFT). This algorithm is also based on interpolation and the polynomial version of the CRT. May 9, 2001 Applied Symbolic Computation 17

Polynomial Algebra mod a Polynomial • A(x) B(x) (mod f(x)) f(x)|(A(x) - B(x)) • This equivalence relation partitions polynomials in F[x] into equivalence classes where the class [A(x)] consists of the set {A(x) + k(x)f(x), where k(x) and f(x) are in F[x]}. • Choose a representative for [A(x)] with degree < deg(f(x)). Can choose rem(A(x), f(x)). • Arithmetic – [A(x)] + [B(x)] = [A(x) + B(x)] – [A(x)] * [B(x)] = [A(x)B(x)] • The set of equivalence classes with arithmetic defined like this is denoted by F[x]/(f(x)) May 9, 2001 Applied Symbolic Computation 18

Modular Inverses Definition: B(x) is the inverse of A(x) mod f(x), if A(x)B(x) 1 (mod f(x)) The equation A(x)B(x) 1 (mod f(x)) has a solution iff gcd(A(x), f(x)) = 1. In particular, if f(x) is irreducible, then F[x]/(f(x)) is a field. By the Extended Euclidean Algorithm, there exist u(x) and v(x) such that A(x)u(x) + B(x)v(x) = gcd(A(x), f(x)). When gcd(A(x), f(x)) = 1, we get A(x)v(x) + f(x)v(x) = 1. Taking this equation mod f(x), we see that A(x)v(x) 1 (mod f(x)) May 9, 2001 Applied Symbolic Computation 19

Polynomial Version of the Chinese Remainder Theorem: Let f(x) and g(x) be polynomials in F[x] (coefficients in a field). Assume that gcd(f(x), g(x)) = 1. For any A 1(x) and A 2(x) there exist a polynomial A(x) with A(x) A 1(x) (mod f(x)) and A(x) A 2(x) (mod g(x)). Theorem: F[x]/(f(x)g(x)) F[x]/(f(x)) F[x]/(g(x)). I. E. There is a 1 -1 mapping from F[x]/(f(x)g(x)) onto F[x]/(f(x)) F[x]/(g(x)) that preserves arithmetic. A(x) (A(x) mod f(x), A(x) mod g(x)) May 9, 2001 Applied Symbolic Computation 20

Constructive Chinese Remainder Theorem: If gcd(f(x), g(x)) = 1, then there exist Ef(x) and Eg(x) (orthogonal idempotents) – – Ef(x) Eg(x) 1 (mod f(x)) 0 (mod g(x)) 0 (mod f(x)) 1 (mod g(x)) It follows that A 1(x) Ef(x) + A 2(x) Eg(x) A 1(x) (mod f(x)) and A 2(x) (mod g(x)). Proof. Since gcd(f(x), g(x)) = 1, by the Extended Euclidean Algorithm, there exist u(x) and v(x) with f(x)u(x) + g(x)v(x) = 1. Set Ef(x) = g(x)v(x) and Eg(x) = f(x)u(x) May 9, 2001 Applied Symbolic Computation 21

Polynomial Evaluation, Interpolation and the CRT • Since A(x) = Q(x)(x- ) + A( ), A(x) A( ) (mod (x- )) • If , then gcd((x- ), (x- )) = 1. Therefore, we can apply the CRT to find a quadratic polynomial A(x) such that A( ) = y and A( ) = z. • A(x) = A( ) E (x) + A( ) E (x), where – E (x) = (x - )/( - ) • Observe that – E ( ) = 1 and E ( ) = 0, so that E (x) 1 (mod (x- )) and E (x) 0 (mod (x- )). The equivalent results hold for E (x) May 9, 2001 Applied Symbolic Computation 22

Multifactor CRT • The CRT can be generalized to the case when we have n pairwise relatively prime polynomials. If f 1(x), …, fn(x) are pairwise relatively prime, i. e. gcd(fi(x), fj(x)) = 1 for i j, then given A 1(x), …, An(x) there exists a polynomial A(x) such that A Ai(x) (mod fi(x)). • Moreover, there exist a system of orthogonal idempotents: E 1(x), …, En(x), such that Ei(x) 1 (mod fi(x)) and Ei(x) 0 (mod fj(x)) for i j. • A(x) = A 1(x)E 1(x) + … + An(x)En(x) May 9, 2001 Applied Symbolic Computation 23

Lagrange Interpolation and the CRT • Assume that 0, 1, …, n are distinct and let fi(x) = (x- i). Then gcd(fi(x), fj(x)) = 1 for i j. • Let • Then Ei(x) 1 (mod fi(x)) and Ei(x) 0 (mod fj(x)) for i j, and Lagrange’s interpolation formula is • A(x) = A ( 0)E 0(x) + … + A( n )En(x) May 9, 2001 Applied Symbolic Computation 24

Matrix Interpretation of Interpolation • The previous system has a solution when the 0, …, n are distinct. The solution can be obtained using Lagrange interpolation. In fact, the inverse of V( 0, …, n) is obtained from the idempotents May 9, 2001 Applied Symbolic Computation 25