Applied Quantitative Methods Lecture 9 Multiple Regression Analysis

Applied Quantitative Methods Lecture 9. Multiple Regression Analysis: Further Issues (Cont. ) November 25 th, 2010

Model Specification Errors Correct specification, no problems Coefficients are biased Standard errors are invalid Correct specification, no problems

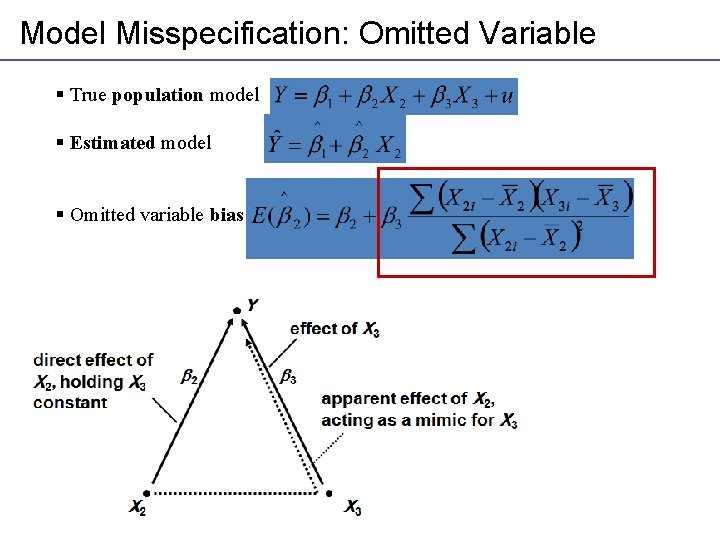
Model Misspecification: Omitted Variable § True population model § Estimated model § Omitted variable bias

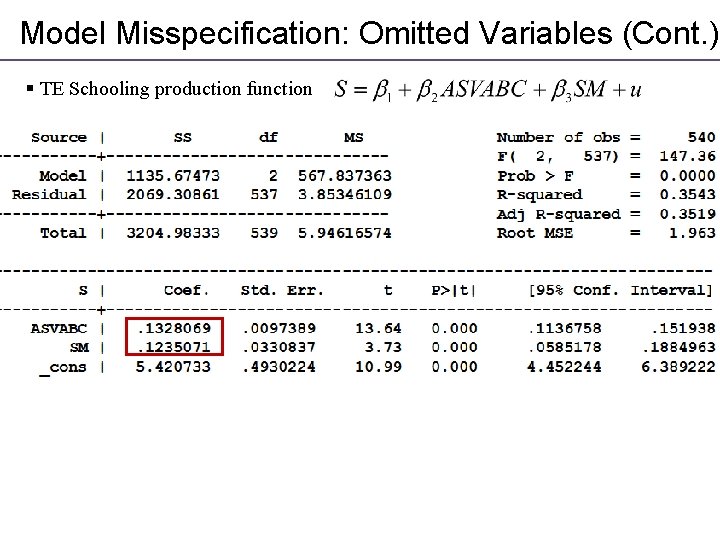
Model Misspecification: Omitted Variables (Cont. ) § TE Schooling production function

Model Misspecification: Omitted Variables (Cont. ) § TE Schooling production function § Estimated model Omitted Variable Bias § Will the bias be positive or negative?

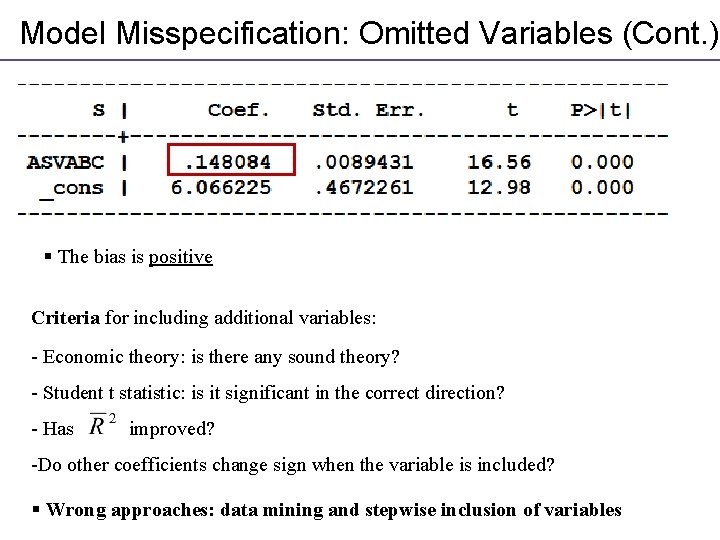
Model Misspecification: Omitted Variables (Cont. ) § The bias is positive Criteria for including additional variables: - Economic theory: is there any sound theory? - Student t statistic: is it significant in the correct direction? - Has improved? -Do other coefficients change sign when the variable is included? § Wrong approaches: data mining and stepwise inclusion of variables

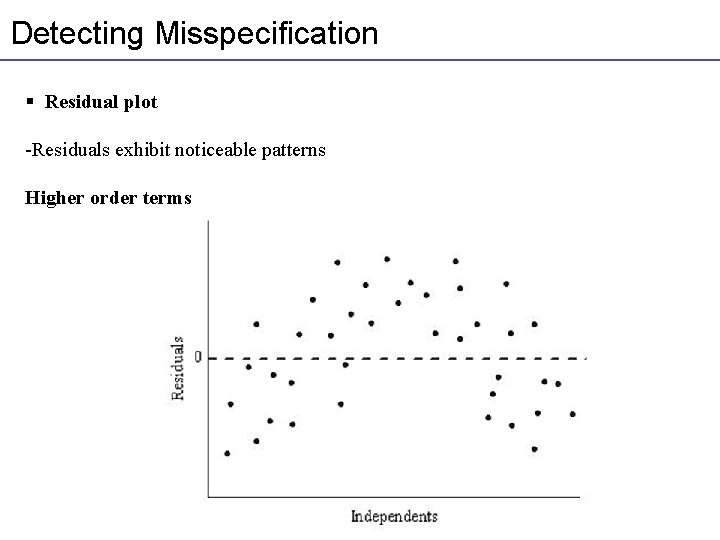
Detecting Misspecification § Residual plot -Residuals exhibit noticeable patterns Higher order terms

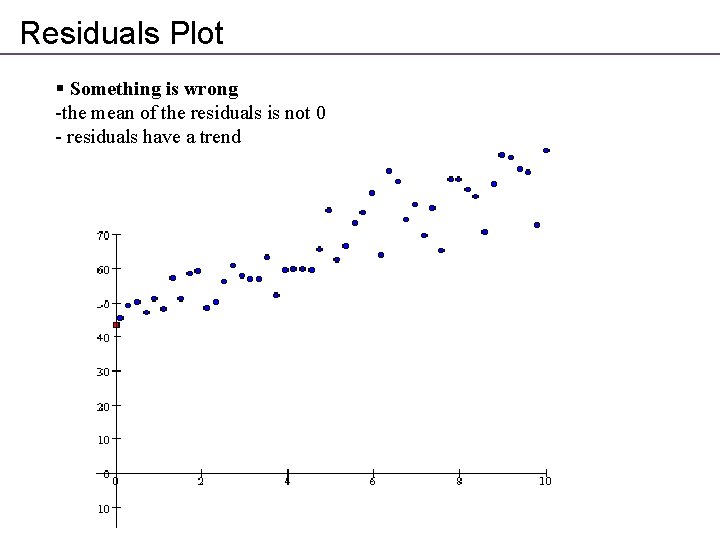
Residuals Plot § Something is wrong -the mean of the residuals is not 0 - residuals have a trend

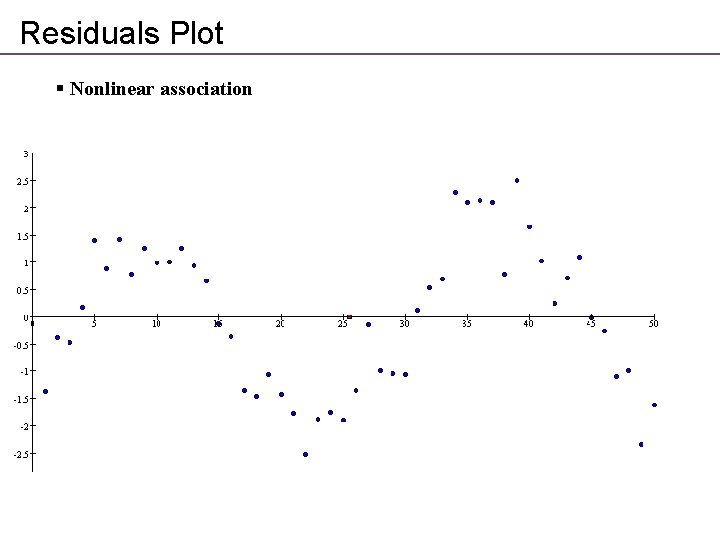
Residuals Plot § Nonlinear association

Unobservable Omitted Variable § Proxy (substitute) True population model Z is a proxy for X 2 Revised model Gain: unbiasedness and valid standard errors Cost: Unable to identify β 2 and β 1 N!B! (Approximately) Same R 2 and t-statistic for Z as in original model TE IQ test score as a proxy for ability

Model Misspecification: Irrelevant Variables Correct specification, no problems Coefficients are unbiased , but inefficient. Standard errors are valid Coefficients are biased (in general). Standard errors are invalid. Correct specification, no problems

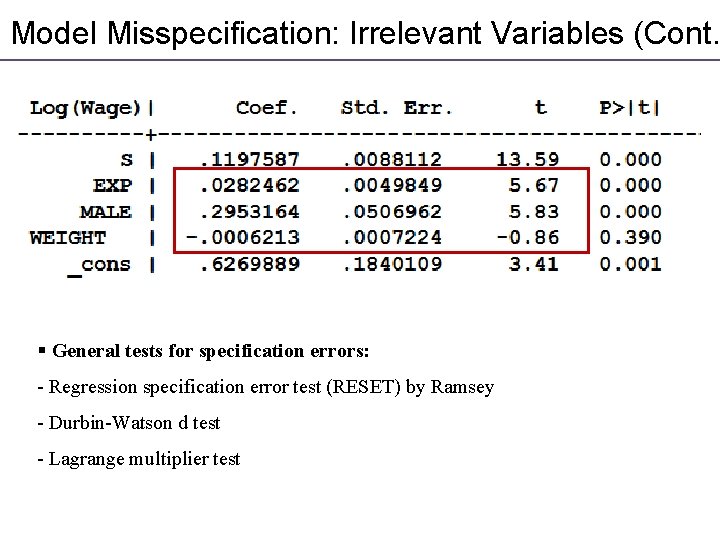
Model Misspecification: Irrelevant Variables (Cont. ) § The cost of overspecification: larger variance of => Loss of efficiency § The coefficient for irrelevant regressor will be insignificant and close to 0 TE Determinants of earnings

Model Misspecification: Irrelevant Variables (Cont. § General tests for specification errors: - Regression specification error test (RESET) by Ramsey - Durbin-Watson d test - Lagrange multiplier test

Multicollinearity § Population model § Exact linear relationship between X 2 and X 3 § Slope coefficient for X 2 is not defined

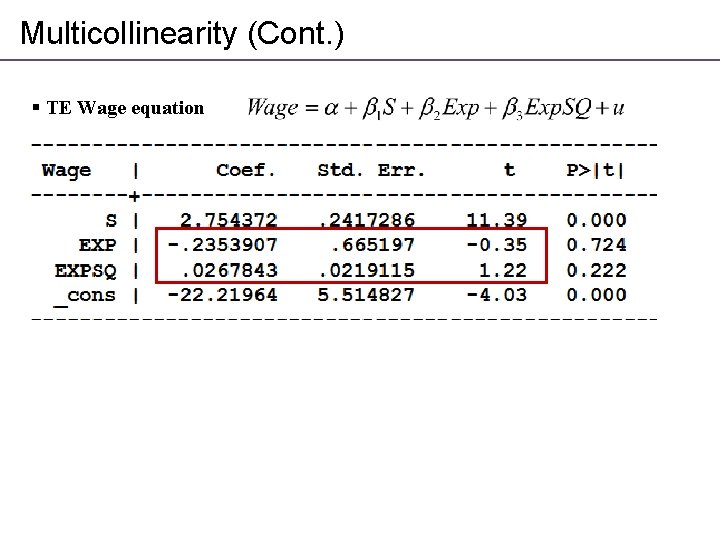
Multicollinearity (Cont. ) § TE Wage equation

Multicollinearity (Cont. ) § Consequences of multicollinearity - Point estimates are not biased but erratic! -Standard errors are valid but large - variance of the disturbance term - number of observations - variability of Xj - correlation between regressors

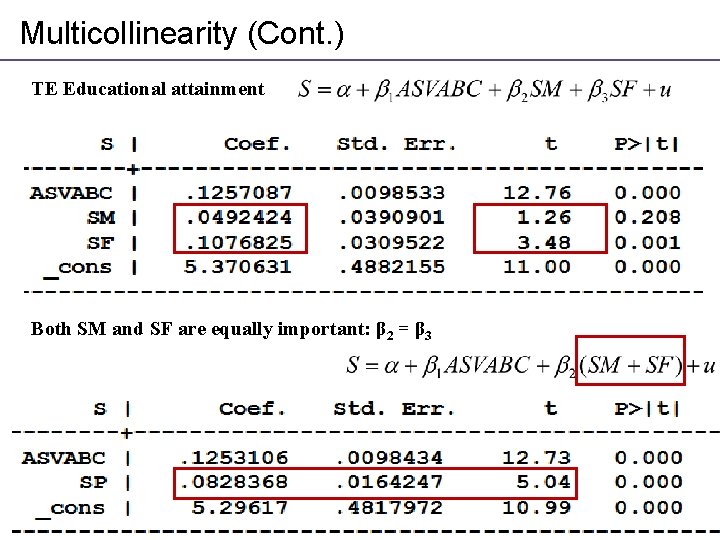
Multicollinearity (Cont. ) TE Educational attainment Both SM and SF are equally important: β 2 = β 3

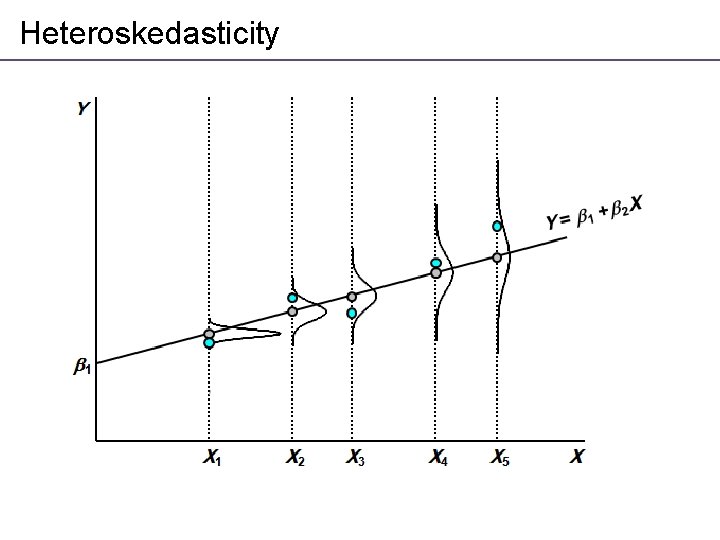
Heteroskedasticity

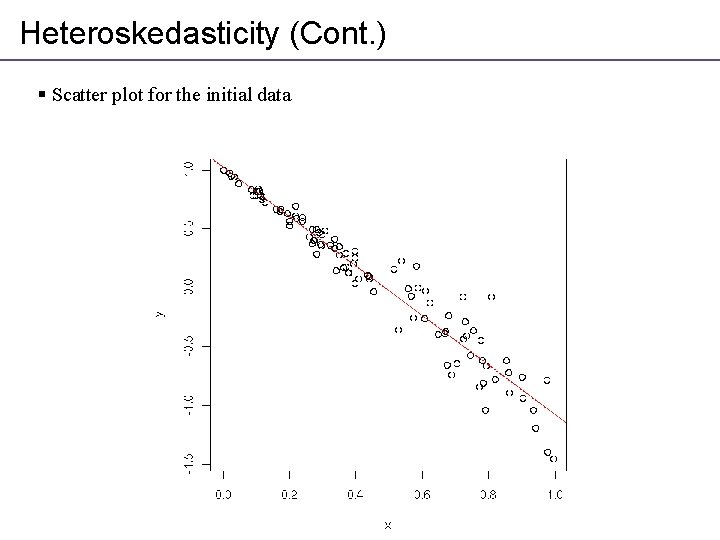
Heteroskedasticity (Cont. ) § Scatter plot for the initial data

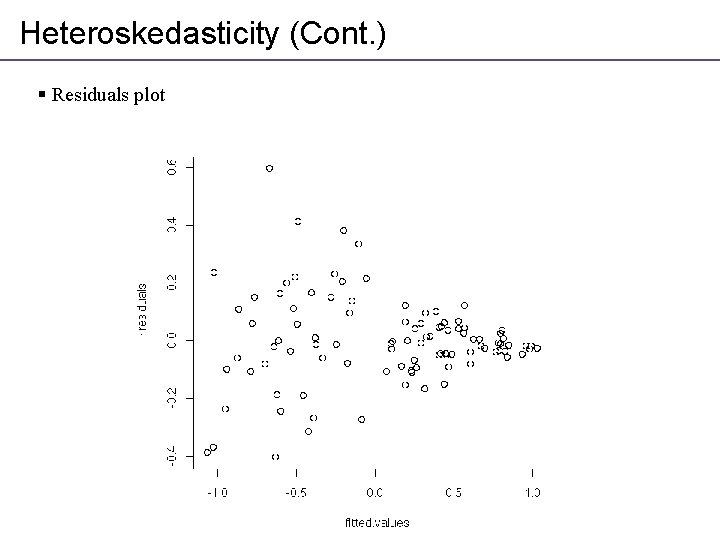
Heteroskedasticity (Cont. ) § Residuals plot

Heteroskedasticity (Cont. ) § Implications for OLS estimates 1. Does not bias estimates of regression coefficients 2. OLS estimates are inefficient - OLS gives equal weight to all observations 3. Standard errors are invalid - Homoskedasticity assumption

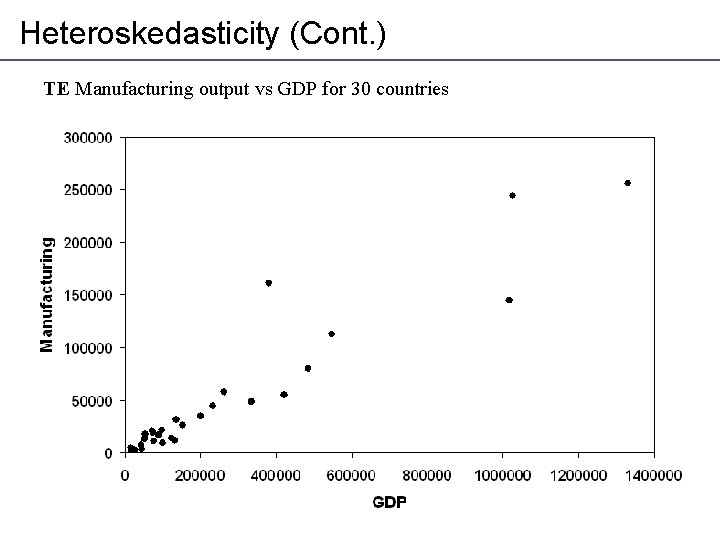
Heteroskedasticity (Cont. ) TE Manufacturing output vs GDP for 30 countries

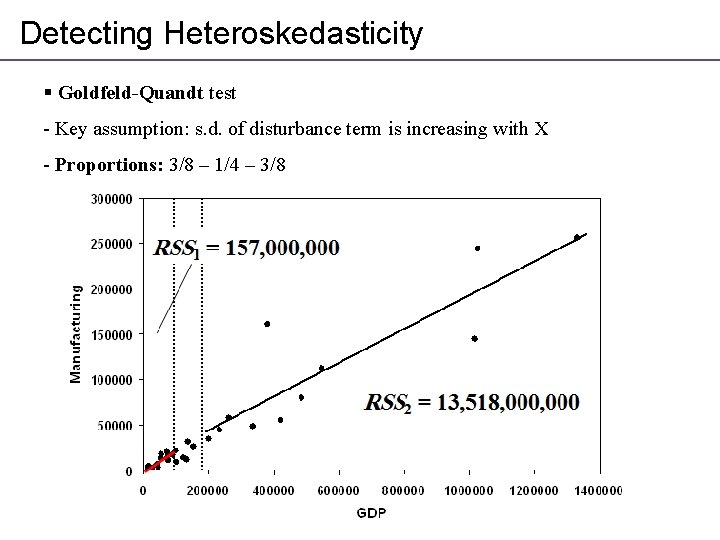
Detecting Heteroskedasticity § Goldfeld-Quandt test - Key assumption: s. d. of disturbance term is increasing with X - Proportions: 3/8 – 1/4 – 3/8

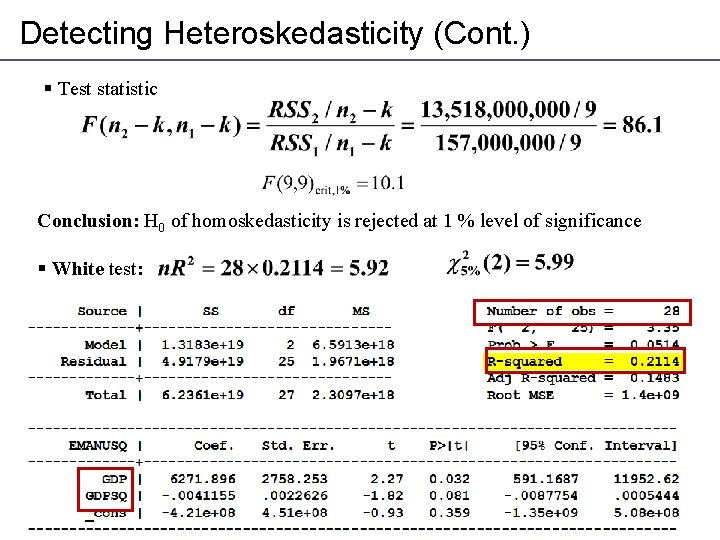
Detecting Heteroskedasticity (Cont. ) § Test statistic Conclusion: H 0 of homoskedasticity is rejected at 1 % level of significance § White test:

Correction for Heteroskedasticity § Weighted OLS § But σi is not known

Correction for Heteroskedasticity § Weighted OLS

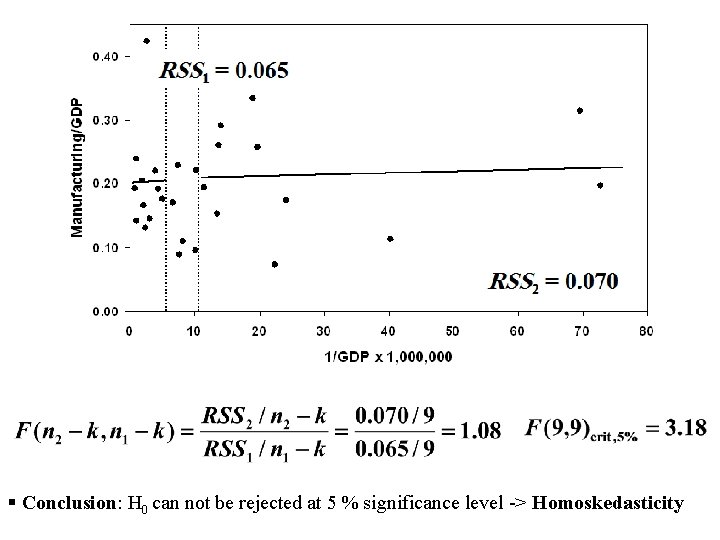
§ Conclusion: H 0 can not be rejected at 5 % significance level -> Homoskedasticity

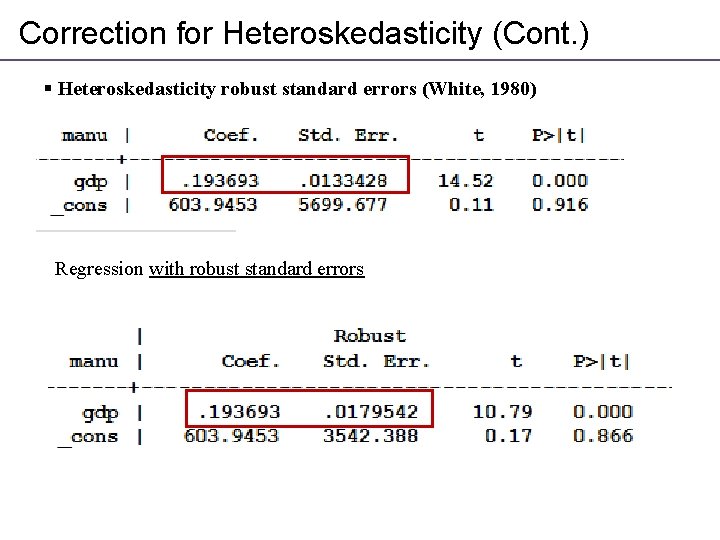
Correction for Heteroskedasticity (Cont. ) § Heteroskedasticity robust standard errors (White, 1980) Regression with robust standard errors

Next Lecture Topic: Dummy Variables ! Wooldridge, Chapter 7& 17. 1 &17. 5 Paper: Heckman, J. (1979). Sample selection bias as a specification error. Econometrica, Vol. 47, No. 1, pp 153161.