Applied Physics Lecture II Electrostatics Coulombs law Electric

Applied Physics Lecture II Ø Electrostatics ü Coulomb’s law ü Electric field Chapter 15 11/26/2020 1

Lightning Review Last lecture: 1. Properties of electric charge ü two types: positive and negative ü always conserved and quantized 2. Insulators and conductors ü charges move freely in conductors; opposite is true for insulators ü conductors can be charged by conduction and induction; insulators can be polarized Review Problem: Operating-room personnel must wear special conducting shoes while working around oxygen. Why? What might happen if personnel wore ordinary rubber shoes (sneakers)? 11/26/2020 2

15. 3 Coulomb’s Law - Observation Charles Coulomb discovered in 1785 the fundamental law of electrical force between two stationary charged particles. An electric force has the following properties: n n n Inversely proportional to the square of the separation, r, between the particles, and is along a line joining them. Proportional to the product of the magnitudes of the charges |q 1| and |q 2| on the two particles. Attractive if the charges are of opposite sign and repulsive if the charges have the same sign. q 1 11/26/2020 q 2 r 3

15. 3 Coulomb’s Law – Mathematical Formulation ke known as the Coulomb constant. Value of ke depends on the choice of units. SI units n n Force: the Newton (N) Distance: the meter (m). Charge: the coulomb ( C). Current: the ampere (A =1 C/s). Experimentally measurement: ke = 8. 9875´ 109 Nm 2/C 2. Reasonable approximate value: ke = 8. 99´ 109 Nm 2/C 2. How do we know the units of ke? 11/26/2020 4

Example: Fun with units Recall that units can be manipulated: 11/26/2020 5

Example Charge and Mass of the Electron, Proton and Neutron. Particle Charge ( C) Mass (kg) Electron -1. 60 ´ 10 -19 9. 11 ´ 10 -31 Proton +1. 60 ´ 10 -19 1. 67 ´ 10 -27 Neutron 0 1. 67 ´ 10 -27 1 e = -1. 60 ´ 10 -19 c Takes 1/e=6. 6 ´ 1018 protons to create a total charge of 1 C Number of free electrons in 1 cm 3 copper ~ 1023 Charge obtained in typical electrostatic experiments with rubber or glass 10 -6 C = 1 mc A very small fraction of the total available charge 11/26/2020 6

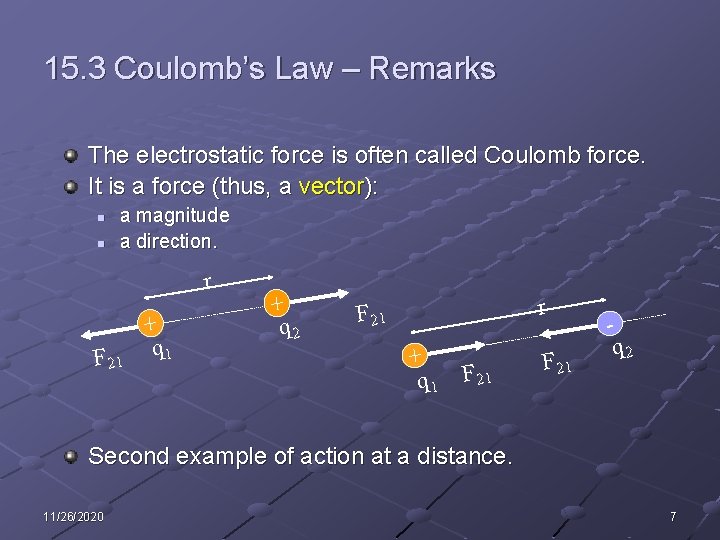
15. 3 Coulomb’s Law – Remarks The electrostatic force is often called Coulomb force. It is a force (thus, a vector): n n a magnitude a direction. r F 21 + q 2 r F 21 + q 1 F 21 q 2 Second example of action at a distance. 11/26/2020 7

Mini-Quiz Name the first action at a distance force you have encountered in physics so far. 11/26/2020 8

Example: Electrical Force Question: The electron and proton of a hydrogen atom are separated (on the average) by a distance of about 5. 3 x 10 -11 m. Find the magnitude of the electric force that each particle exerts on the other. 11/26/2020 9

Question: The electron and proton of a hydrogen atom are separated (on the average) by a distance of about 5. 3 x 10 -11 m. Find the magnitude of the electric force that each particle exerts on the other. Observations: We are interested in finding the magnitude of the force between two particles of known charge, and a given distance of each other. The magnitude is given by Coulomb’s law. q 1 =-1. 60 x 10 -19 C q 2 =1. 60 x 10 -19 C r = 5. 3 x 10 -11 m 11/26/2020 10

Question: The electron and proton of a hydrogen atom are separated (on the average) by a distance of about 5. 3 x 10 -11 m. Find the magnitude of the electric force that each particle exerts on the other. Observations: We are interested in finding the magnitude of the force between two particles of known charge, and a given distance of each other. The magnitude is given by Coulomb’s law. q 1 =-1. 60 x 10 -19 C q 2 =1. 60 x 10 -19 C r = 5. 3 x 10 -11 m Solution: Attractive force with a magnitude of 8. 2 x 10 -8 N. 11/26/2020 11

Superposition Principle From observations: one finds that whenever multiple charges are present, the net force on a given charge is the vector sum of all forces exerted by other charges. Electric force obeys a superposition principle. 11/26/2020 12

Example: Using the Superposition Principle Consider three point charges at the corners of a triangle, as shown below. Find the resultant force on q 3 if q 1 = 6. 00 x 10 -9 C q 2 = -2. 00 x 10 -9 C q 3 = 5. 00 x 10 -9 C y q 2 F 31 - 3. 00 m q 1 + 11/26/2020 4. 00 m F 32 + q 3 37. 0 o x 13

Consider three point charges at the corners of a triangle, as shown below. Find the resultant force on q 3. y q 2 F 31 - 3. 00 m q 1 + 4. 00 m F 32 + q 3 37. 0 o x Observations: The superposition principle tells us that the net force on q 3 is the vector sum of the forces F 32 and F 31. The magnitude of the forces F 32 and F 31 can calculated using Coulomb’s law. 11/26/2020 14

Consider three point charges at the corners of a triangle, as shown below. Find the resultant force on q 3. y q 2 3. 00 m - q 1 + 4. 00 m F 32 5. 00 m F 31 + q 3 37. 0 o x Solution: 11/26/2020 15

15. 4 Electric Field - Discovery Electric forces act through space even in the absence of physical contact. Suggests the notion of electrical field (first introduced by Michael Faraday (1791 -1867). An electric field is said to exist in a region of space surrounding a charged object. If another charged object enters a region where an electrical field is present, it will be subject to an electrical force. 11/26/2020 16

15. 4 Electric Field – Quantitative Definition A field : generally changes with position (location) A vector quantity : magnitude and direction. Magnitude at a given location n 11/26/2020 Expressed as a function of the force imparted by the field on a given test charge. 17

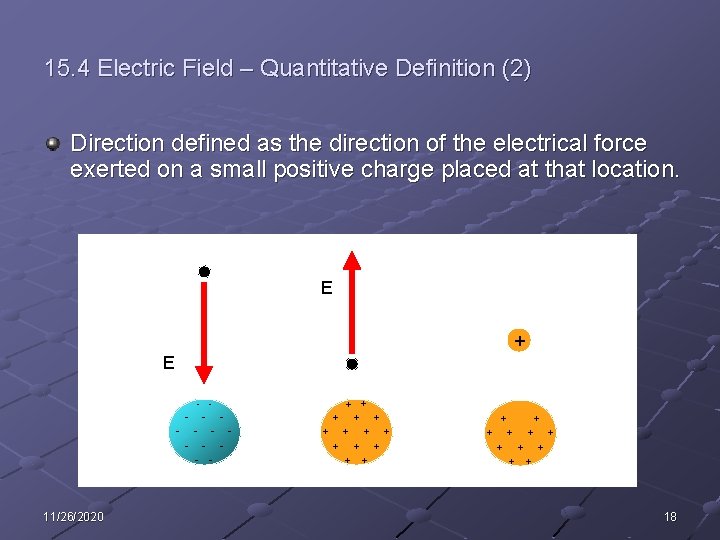
15. 4 Electric Field – Quantitative Definition (2) Direction defined as the direction of the electrical force exerted on a small positive charge placed at that location. E + E - - - - - 11/26/2020 + + - + + + + + + 18

15. 4 Electric Field – Electric Field of a Charge “q” Given One finds 11/26/2020 19

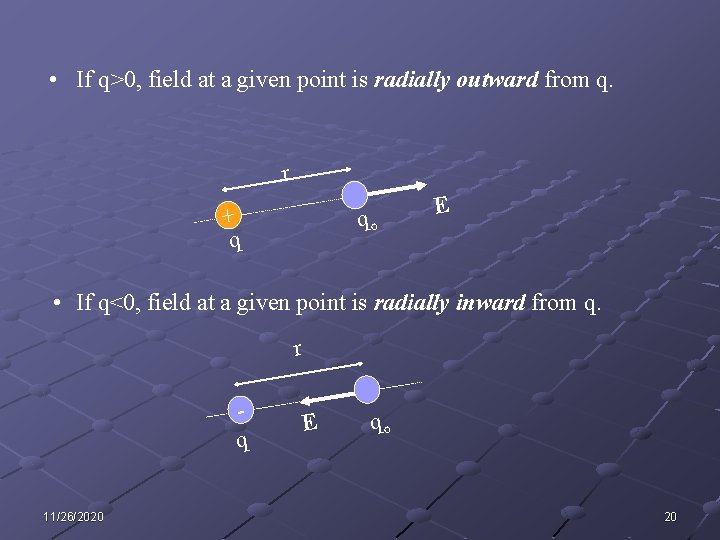
• If q>0, field at a given point is radially outward from q. r + q qo E • If q<0, field at a given point is radially inward from q. r q 11/26/2020 E qo 20

Problem-Solving Strategy Electric Forces and Fields n Units: For calculations that use the Coulomb constant, ke, charges must be in coulombs, and distances in meters. Conversion are required if quantities are provided in other units. n Applying Coulomb’s law to point charges. It is important to use the superposition principle properly. Determine the individual forces first. Determine the vector sum. Determine the magnitude and/or the direction as needed. 11/26/2020 21

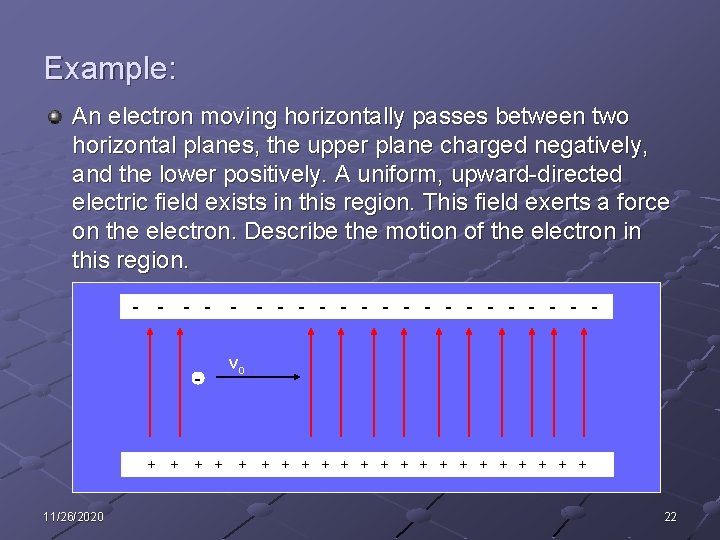
Example: An electron moving horizontally passes between two horizontal planes, the upper plane charged negatively, and the lower positively. A uniform, upward-directed electric field exists in this region. This field exerts a force on the electron. Describe the motion of the electron in this region. - - - + 11/26/2020 + + + - - - - - vo + + + + + 22

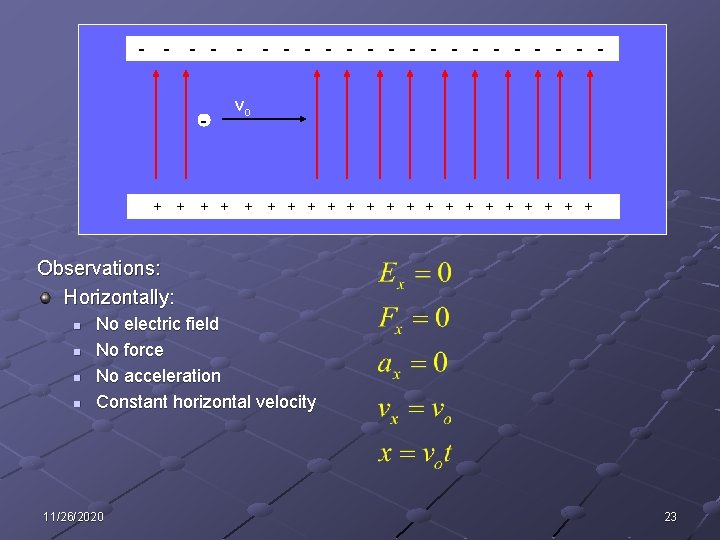
- - - + + - - - - - vo + + + + + Observations: Horizontally: n n No electric field No force No acceleration Constant horizontal velocity 11/26/2020 23

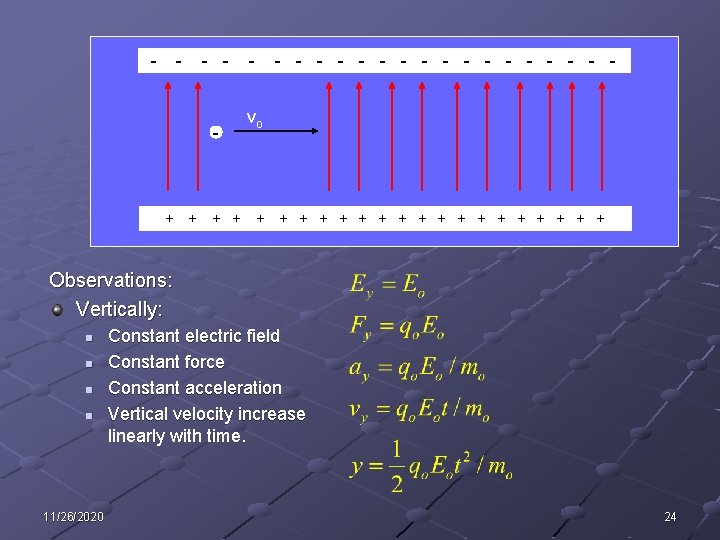
- - - + + - - - - - vo + + + + + Observations: Vertically: n n 11/26/2020 Constant electric field Constant force Constant acceleration Vertical velocity increase linearly with time. 24

- - - - - - + + + + + + Conclusions: The charge will follow a parabolic path downward. Motion similar to motion under gravitational field only except the downward acceleration is now larger. 11/26/2020 25

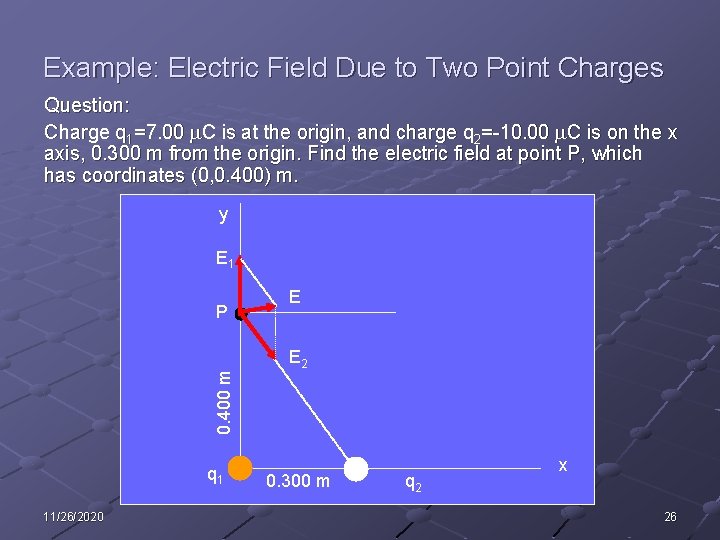
Example: Electric Field Due to Two Point Charges Question: Charge q 1=7. 00 m. C is at the origin, and charge q 2=-10. 00 m. C is on the x axis, 0. 300 m from the origin. Find the electric field at point P, which has coordinates (0, 0. 400) m. y E 1 P E 0. 400 m E 2 q 1 11/26/2020 0. 300 m q 2 x 26

Question: Charge q 1=7. 00 m. C is at the origin, and charge q 2=-10. 00 m. C is on the x axis, 0. 300 m from the origin. Find the electric field at point P, which has coordinates (0, 0. 400) m. Observations: First find the field at point P due to charge q 1 and q 2. Field E 1 at P due to q 1 is vertically upward. Field E 2 at due to q 2 is directed towards q 2. The net field at point P is the vector sum of E 1 and E 2. The magnitude is obtained with 11/26/2020 27

Question: Charge q 1=7. 00 m. C is at the origin, and charge q 2=-10. 00 m. C is on the x axis, 0. 300 m from the origin. Find the electric field at point P, which has coordinates (0, 0. 400) m. Solution: 11/26/2020 28

15. 5 Electric Field Lines A convenient way to visualize field patterns is to draw lines in the direction of the electric field. Such lines are called field lines. Remarks: 1. 2. Electric field vector, E, is tangent to the electric field lines at each point in space. The number of lines per unit area through a surface perpendicular to the lines is proportional to the strength of the electric field in a given region. E is large when the field lines are close together and small when far apart. 11/26/2020 29

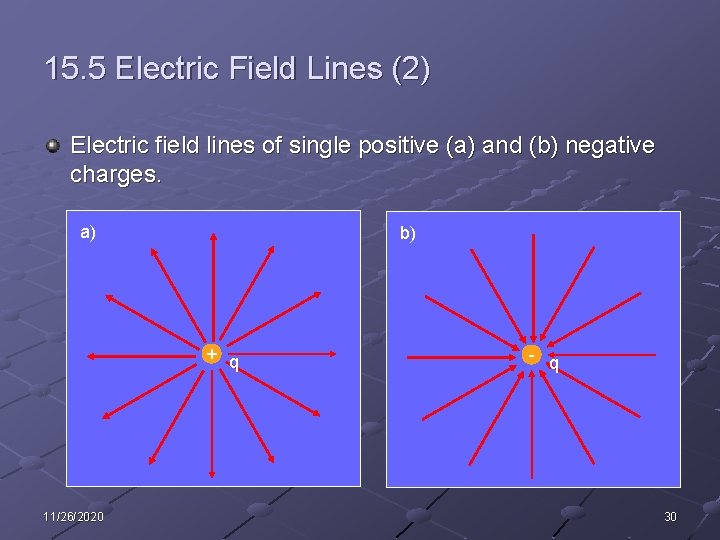
15. 5 Electric Field Lines (2) Electric field lines of single positive (a) and (b) negative charges. a) b) + q 11/26/2020 - q 30

15. 5 Electric Field Lines (3) Rules for drawing electric field lines for any charge distribution. 1. 2. 3. 11/26/2020 Lines must begin on positive charges (or at infinity) and must terminate on negative charges or in the case of excess charge at infinity. The number of lines drawn leaving a positive charge or approaching a negative charge is proportional to the magnitude of the charge. No two field lines can cross each other. 31

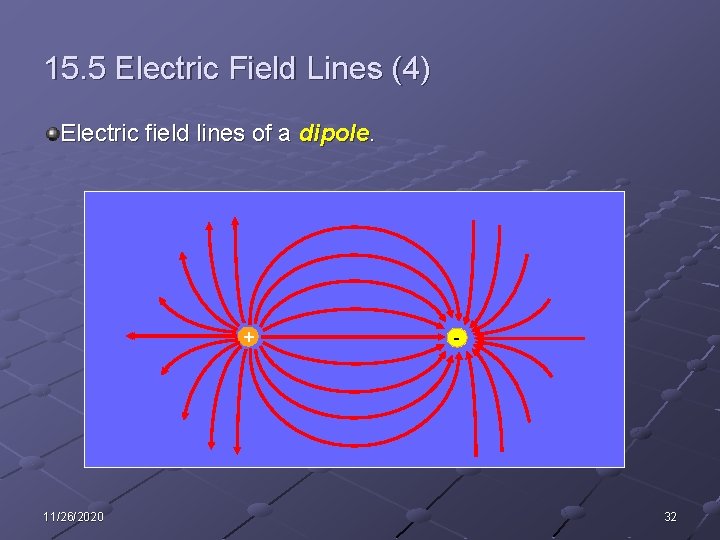
15. 5 Electric Field Lines (4) Electric field lines of a dipole. + 11/26/2020 - 32

Application: Measurement of the atmospheric electric field The electric field near the surface of the Earth is about 100 N/C downward. Under a thundercloud, the electric field can be as large as 20000 N/C. How can such a (large) field be measured? A 11/26/2020 33

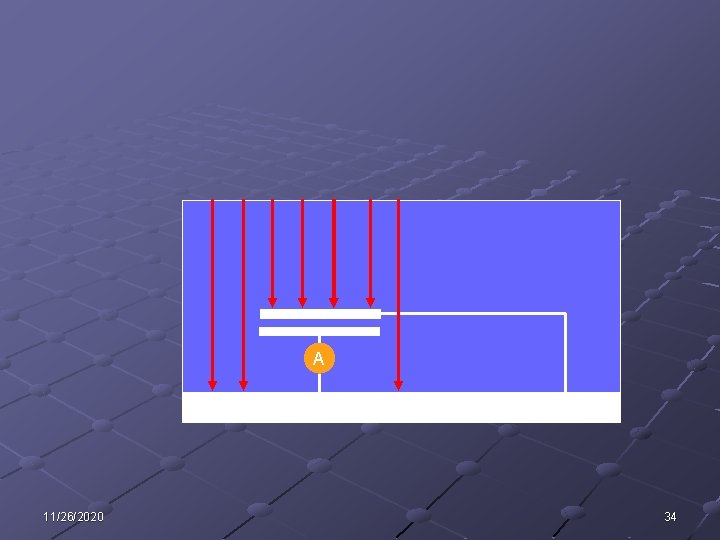
A 11/26/2020 34

15. 6 Conductors in Electrostatic Equilibrium Good conductors (e. g. copper, gold) contain charges (electron) that are not bound to a particular atom, and are free to move within the material. When no net motion of these electrons occur the conductor is said to be in electro-static equilibrium. 11/26/2020 35

15. 6 Conductors in Electrostatic Equilibrium Properties of an isolated conductor (insulated from the ground). 1. 2. 3. 4. 11/26/2020 Electric field is zero everywhere within the conductor. Any excess charge field on an isolated conductor resides entirely on its surface. The electric field just outside a charged conductor is perpendicular to the conductor’s surface. On an irregular shaped conductor, the charge tends to accumulate at locations where the radius of curvature of the surface is smallest – at sharp points. 36

1. Electric field is zero everywhere within the conductor. If this was not true, the field inside would be finite. Free charge there would move under the influence of the field. A current would be induced. The conductor would not be in an electrostatic state. 11/26/2020 37

2. Any excess charge field on an isolated conductor resides entirely on its surface. This property is a direct result of the 1/r 2 repulsion between like charges. If an excess of charge is placed within the volume, the repulsive force pushes them as far apart as they can go. They thus migrate to the surface. 11/26/2020 38

3. The electric field just outside a charged conductor is perpendicular to the conductor’s surface. If not true, the field would have components parallel to the surface of the conductor. This field component would cause free charges of the conductor to move. A current would be created. There would no longer be a electro-static equilibrium. 11/26/2020 39

4. On an irregular shaped conductor, the charge tends to accumulate at locations where the radius of curvature of the surface is smallest – at sharp points. Consider, for instance, a conductor fairly flat at one end and relatively pointed at the other. Excess of charge move to the surface. Forces between charges on the flat surface, tend to be parallel to the surface. Those charges move apart until repulsion from other charges creates an equilibrium. At the sharp ends, the forces are predominantly directed away from the surface. There is less of tendency for charges located at sharp edges to move away from one another. Produces large fields (and force) near sharp edges. - 11/26/2020 - 40

Remarks Property 4 is the basis for the use of lightning rods near houses and buildings. (Very important application) n n Most of any charge on the house will pass through the sharp point of the lightning rod. First developed by B. Franklin. 11/26/2020 41

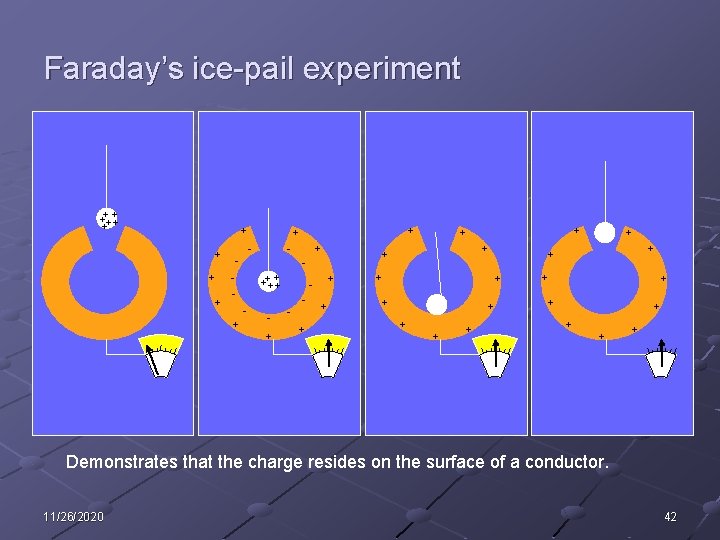
Faraday’s ice-pail experiment +++++ + + - - - + +++++ + + + + - + + + + + Demonstrates that the charge resides on the surface of a conductor. 11/26/2020 42

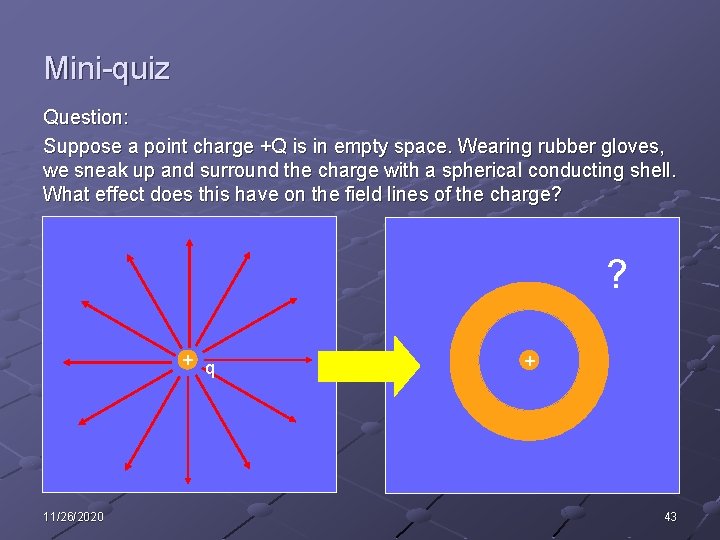
Mini-quiz Question: Suppose a point charge +Q is in empty space. Wearing rubber gloves, we sneak up and surround the charge with a spherical conducting shell. What effect does this have on the field lines of the charge? ? + q 11/26/2020 + 43

Question: Suppose a point charge +Q is in empty space. Wearing rubber gloves, we sneak up and surround the charge with a spherical conducting shell. What effect does this have on the field lines of the charge? Answer: Negative charge will build up on the inside of the shell. Positive charge will build up on the outside of the shell. There will be no field lines inside the conductor but the field lines will remain outside the shell. + + - + q - + + - - + 11/26/2020 + - - + + 44

Mini-Quiz Question: Is it safe to stay inside an automobile during a lightning storm? Why? 11/26/2020 45

Question: Is it safe to stay inside an automobile during a lightning storm? Why? Answer: Yes. It is. The metal body of the carries the excess charges on its external surface. Occupants touching the inner surface are in no danger. SAFE 11/26/2020 46