Applied Geostatistics Notes on Introduction to Spatial Autocorrelation

Applied Geostatistics Notes on Introduction to Spatial Autocorrelation Week 4 – April 18, 2005 --------------------------------Geostatistical methods were developed for interpreting data that varies continuously over a predefined, fixed spatial region. The study of geostatistics assumes that at least some of the spatial variation observed for natural phenomena can be modeled by random processes with spatial autocorrelation. Geostatistics is based on theory of regionalized variables, variable distributed in space (or time). Geostatiscal theory supports that any measurement of regionalozed variables can be viewed as a realization of a random function (or random process, or random field, or stochastic process)

Spatial Structure Geostatisticals techniques are designed to evaluate the spatial structure of a variable, or the relationship between a value measured at a point in one place, versus a value from another point measured a certain distance away. Describing spatial structure is useful for: § Indicating intensity of pattern and the scale at which that pattern is exposed § Interpolating to predict values at unmeasured points across the domain (e. g. kriging) § Assessing independence of variables before applying parametric tests of significance

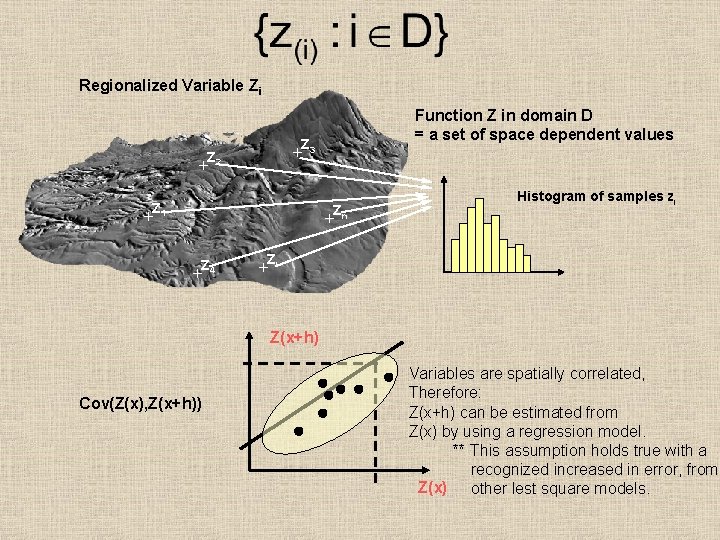
Regionalized Variable Zi Function Z in domain D = a set of space dependent values Z 3 + Z 2 + Z 1 Zn + Histogram of samples zi + Z 4 + Zi + Z(x+h) Cov(Z(x), Z(x+h)) Variables are spatially correlated, Therefore: Z(x+h) can be estimated from Z(x) by using a regression model. ** This assumption holds true with a recognized increased in error, from Z(x) other lest square models.

Regionalized Variables take on values according to spatial location. Given a variable z, measured at a location i , the variability in z can be broken down into three components: Where: Usually removed by detrending A “structural” coarse scale forcing or trend A random” Local spatial dependency What we are interested in error variance (considered normally distributed) Coarse scale forcing or trends can be removed by fitting a surface to the trend using regression and then working with regression residuals

Correlation: calculated using the geometric rather than the arithmetric mean Two distributions One distribution ) θ 2 a )θ ) b a θ 1 b As θ decreases, a/b goes to 0 x y x·y x 2 y 2 Sum of squares Y 3 2 5 3 : : µ Product of Deviations X 1 3 2 1 : : µ deviates Deviations data If you were to calculate correlation by hand …. You would produce these Terms.

Spatial Autocorrelation A variable is thought to be autocorrelated if it is possible to predict its value at a given location, by knowing its value at other nearby locations. Positive autocorrelation: Negative autocorrelation: No autocorrelation: § Autocorrelation is evaluated using structure functions that assess the spatial structure or dependency of the variable. § Two of these functions are autocorrelation and semivariance which are graphed as a correlogram and semivariogram, respectively. § Both functions plot the spatial dependence of the variable against the spatial separation or lag distance.

Moran I (1950) • A cross-product statistic that is used to describe autocorrelation • Compares value of a variable at one location with values at all other locations Where: n is the number of pairs Zi is the deviation from the mean for value at location i (i. e. , Zi = yi – y for variable y) Zj is the deviation from the mean for value at location j (i. e. , Zj = yj – y for variable y) wij is an indicator function or weight at distance d (e. g. wij = 1, if j is in distance class d from point i, otherwise = 0) Wij is the sum of all weights (number of pairs in distance class) The numerator is a covariance (cross-product) term; the denominator is a variance term. Values range from [-1, 1] Value = 1 : Perfect positive correlation Value = -1: Perfect negative correlation

GEARY C (1954) • A squared difference statistic for assessing spatial autocorrelation • Considers differences in values between pairs of observations, rather than the covariation between the pairs (Moran I) The numerator in this equation is a distance term that gets squared. The Geary C statistic is more sensitive to extreme values & clustering than the Moran I. Values range from [0, 3] Value = 1 : No autocorrelation Value = 0 : Positive autocorrelation Value > 1 : Negative autocorrelation

Semivariance The geostatistical measure that describes the rate of change of the regionalized variable is known as the semivariance. Semivariance is used for descriptive analysis where the spatial structure of the data is investigated using the semivariogram and for predictive applications where the semivariogram is fitted to a theoretical model, parameterized, and used to predict the regionalized variable at other non-measured points (kriging). Where : j is a point at distance d from i nd is the number of points in that distance class (i. e. , the sum of the weights wij for that distance class) wij is an indicator function set to 1 if the pair of points is within the distance class.

A semivariogram is a plot of the structure function that, like autocorrelation, describes the relationship between measurements taken some distance apart. Semivariograms define the range or distance over which spatial dependence exists. §The nugget is the semivariance at a distance 0. 0, (the y –intercept) §The sill is the value at which the semivariogram levels off (its asymptotic value) §The range is the distance at which the semivariogram levels off (the spatial extent of structure in the data)

Stationarity Autocorrelation assumes stationarity, meaning that the spatial structure of the variable is consistent over the entire domain of the dataset. The stationarity of interest is second-order (weak) stationarity, requiring that: (a) the mean is constant over the region (b) variance is constant and finite; and (c) covariance depends only on between-sample spacing § § § In many cases this is not true because of larger trends in the data In these cases, the data are often detrended before analysis. One way to detrend data is to fit a regression to the trend, and use only the residuals for autocorrelation analysis

Anistotropy Autocorrelation also assumes isotropy, meaning that the spatial structure of the variable is consistent in all directions. Often this is not the case, and the variable exhibits anisotropy, meaning that there is a direction-dependent trend in the data. If a variable exhibits different ranges in different directions, then there is a geometric anisotropy. For example, in a dune deposit, permeability might have a larger range in the wind direction compared to the range perpendicular to the wind direction. If the variable exhibits different sills in different directions, then there is a zonal anisotropy. For example, a variogram in a vertical wellbore typically shows a bigger sill than a variogram in the horizontal direction. Some variograms are a combination of both geometric and zonal anisotropies.

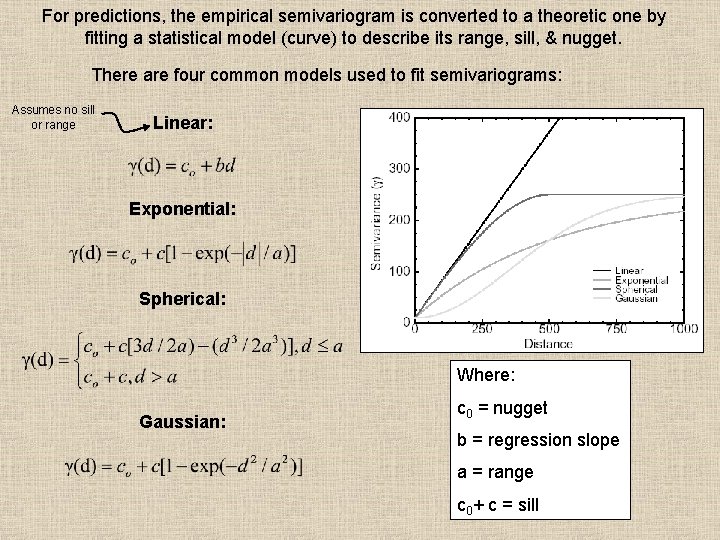
For predictions, the empirical semivariogram is converted to a theoretic one by fitting a statistical model (curve) to describe its range, sill, & nugget. There are four common models used to fit semivariograms: Assumes no sill or range Linear: Exponential: Spherical: Where: Gaussian: c 0 = nugget b = regression slope a = range c 0+ c = sill

Variogram Modeling Suggestions • Check for enough number of pairs at each lag distance (from 30 to 50). • Removal of outliers • Truncate at half the maximum lag distance to ensure enough pairs • Use a larger lag tolerance to get more pairs and a smoother variogram • Start with an omnidirectional variogram before trying directional variograms • Use other variogram measures to take into account lag means and variances (e. g. , inverted covariance, correlogram, or relative variograms) • Use transforms of the data for skewed distributions (e. g. logarithmic transforms). • Use the mean absolute difference or median absolute difference to derive the range