APPLIED GEOPHYSICS POTENTIAL FIELD METHODS JEANNOT TRAMPERT GAUSS


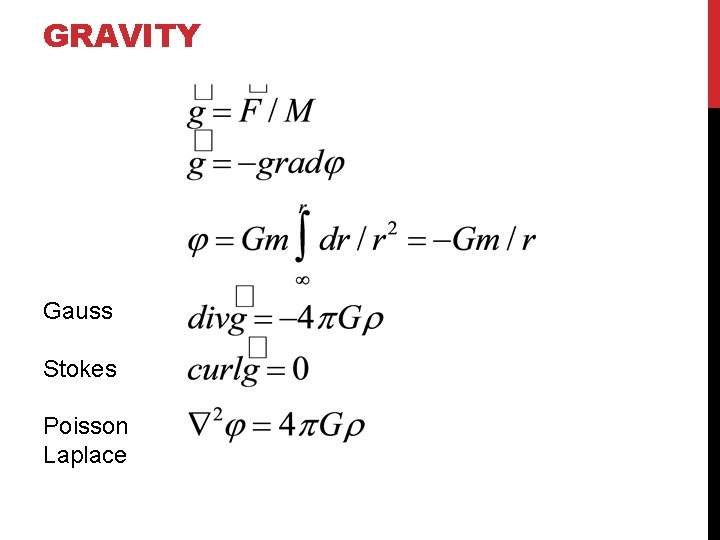













- Slides: 26

APPLIED GEOPHYSICS POTENTIAL FIELD METHODS JEANNOT TRAMPERT

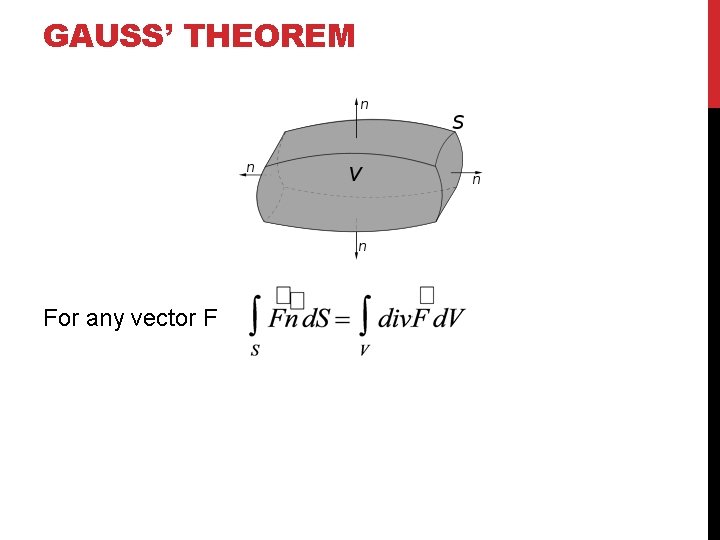
GAUSS’ THEOREM For any vector F

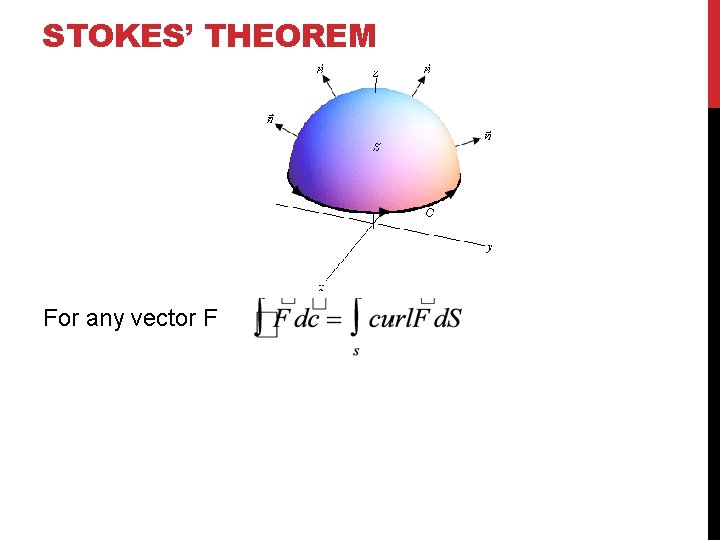
STOKES’ THEOREM For any vector F

POTENTIAL FIELD THEORY irrotational conservative field A force F derives from a scalar potential Φ if The work done by force F (see Stokes)

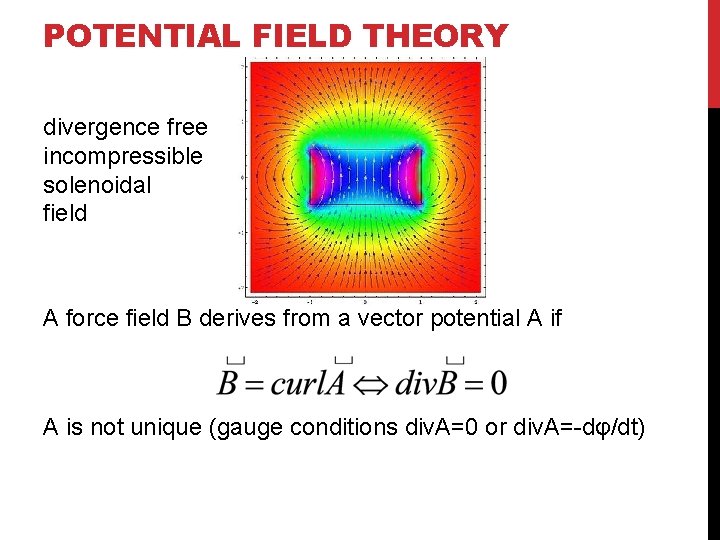
POTENTIAL FIELD THEORY divergence free incompressible solenoidal field A force field B derives from a vector potential A if A is not unique (gauge conditions div. A=0 or div. A=-dφ/dt)

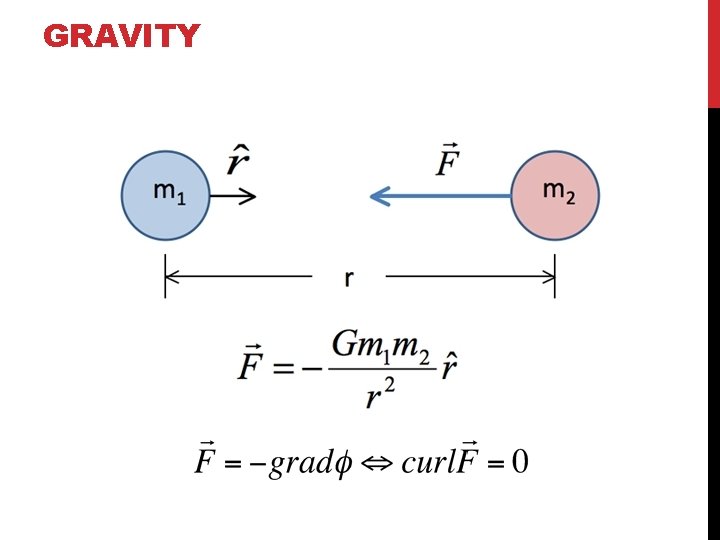
GRAVITY
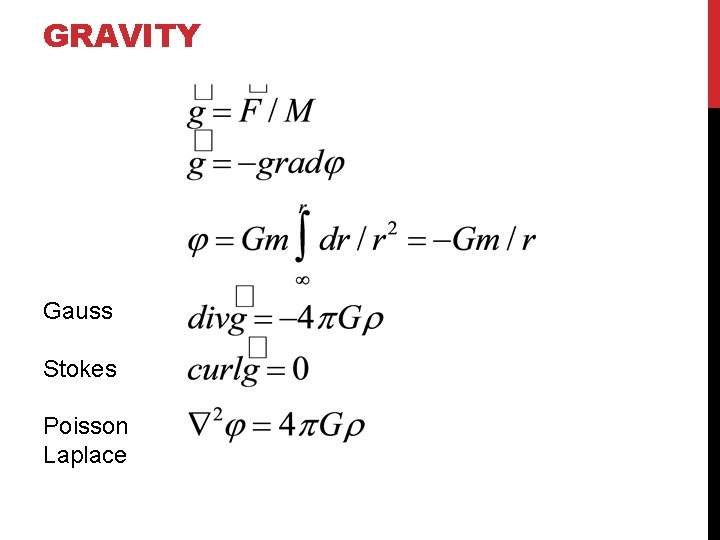
GRAVITY Gauss Stokes Poisson Laplace

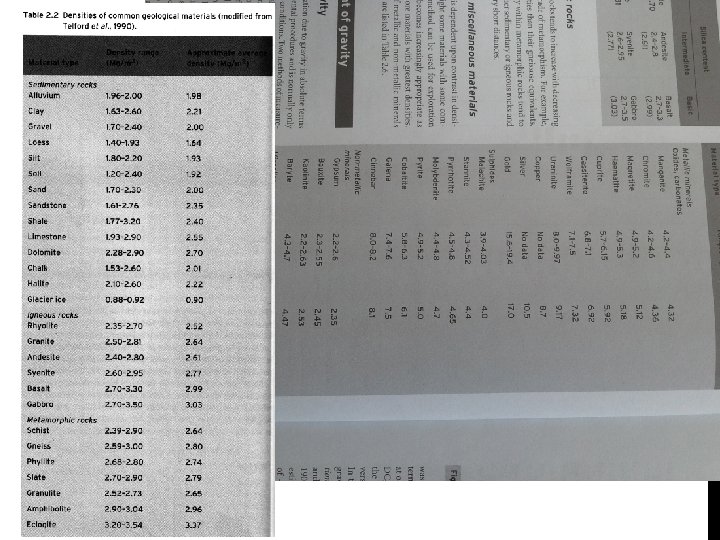
GRAVITY Gravity measures spatial variations of the gravitational field due to lateral variations in density.



ELECTROSTATICS (CHARGES AT REST)

ELECTROSTATICS (CHARGES AT REST) Gauss Stokes Poisson Laplace ε = permittivity

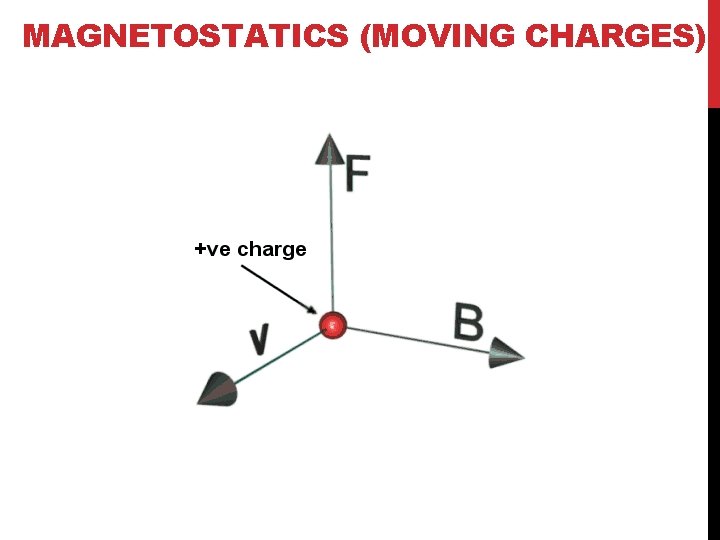
MAGNETOSTATICS (MOVING CHARGES)

MAGNETOSTATICS (MOVING CHARGES) Lorentz Ampere μ = permeability If no currents (j=0) B derives from a scalar potential

BOUNDARY VALUE PROBLEMS Poisson Laplace • ρ is a source term • Solutions to the Laplace equation are called harmonic functions • Poisson and Laplace are elliptic pde • Boundary value problem: Find φ in a volume V given the source and additional information on the surface: • Dirichlet: φ specified on the surface • Neumann: gradφ specified on the surface

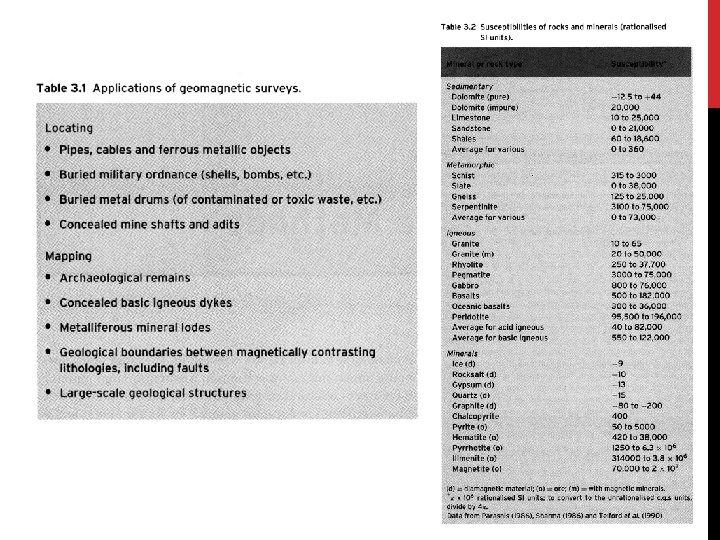
MAGNETOSTATICS Geomagnetics measures spatial variations of the intensity of the magnetic field due to lateral variations in magnetic susceptibility.


ELECTROMAGNETICS MOVING CHARGES IN TIME VARYING FIELDS Maxwell’s equations

ELECTRO MAGNETICS

GRAVITY METHOD The acceleration of a mass m due to another mass M at a distance r is given by We can only directly measure g in the vertical direction. In exploration, we usually directly deal with g, in large scale problems it is easier to work with the scalar potential (geoid)

GRAVITY METHOD The contributions are summed in the vertical direction. Unit: 1 m/s 2 Earth surface 9. 8 m/s 2 980 cm/s 2 980 Gal 980000 m. Gal anomalies order of m. Gal

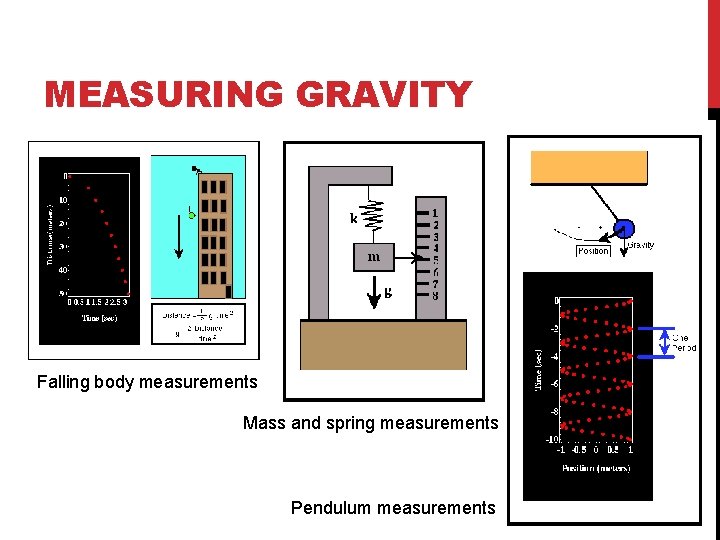
MEASURING GRAVITY Falling body measurements Mass and spring measurements Pendulum measurements

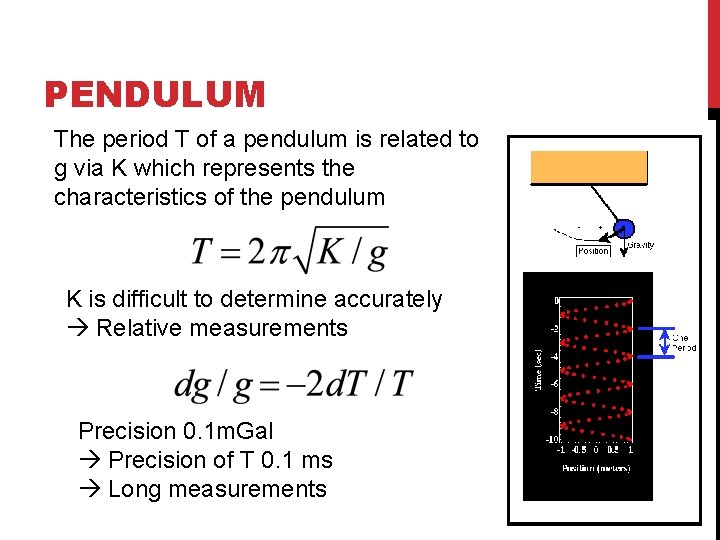
PENDULUM The period T of a pendulum is related to g via K which represents the characteristics of the pendulum K is difficult to determine accurately Relative measurements Precision 0. 1 m. Gal Precision of T 0. 1 ms Long measurements

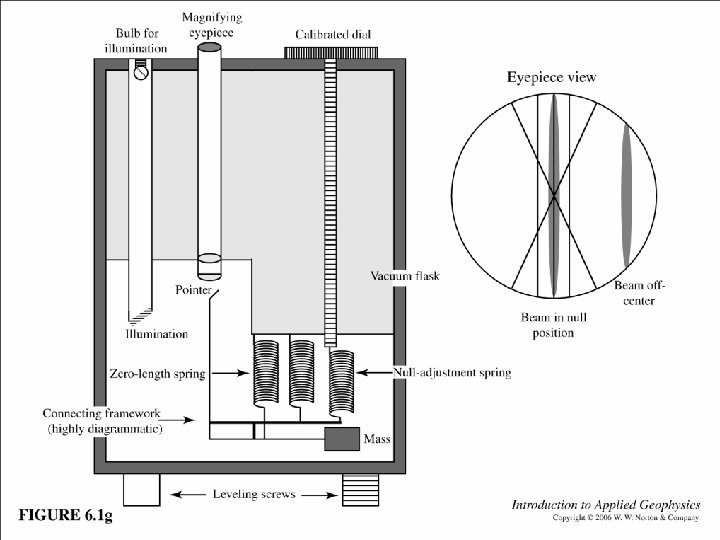
MASS ON SPRING Lacoste introduced a zero-length spring (tension proportional to length) first used in the Lacoste-Romberg gravitymeter. Zero length-string is very sensitivity to small changes in g. In the Worden gravitymeter spring and lever are made from quartz minimizes temperature changes 0. 01 m. Gal precision


ABSOLUTE GRAVITY MEASUREMENTS If we only survey a small region, relative measurements are enough (assume reference g), but comparing different regions requires the knowledge of absolute gravity. IGSN-71 Absolute measurements (z=gt 2/2)