Applied Geometry Lesson 2 2 Segments and Properties

Betweeness: Point R is between points P & Q if and only if R,

Example Points A, B, and C are collinear. If AB = 12, BC =

Example Points R, S, and T are collinear. If RS = 42, ST =

Equation A statement that includes the symbol = Shows that 2 things are of

Properties of Equality Reflexive a=a Symmetric If a = b, then b = a

Properties Addition / subtraction If a = b then a + c = b

Example If QS = 29 and QT = 52, find ST. Find the relationship

Example If PR = 27 and PT = 73, find RT. PT = PR

Measurement: made up of 2 parts l Measure 10 l Unit of measure cm

Precision: depends on the smallest unit used to make the measurement Greatest possible error:

Precision 5. 7 cm or 57 mm Precision: 1 mm Greatest possible error: 0.

Precision example Precision: 1/16 in smallest unit on ruler Greatest possible error: 1/32 in

Slides: 13

Download presentation

Applied Geometry Lesson 2 – 2 Segments and Properties of Real Numbers Objective: Learn to apply the properties of real #s to the measure of segments

Betweeness: Point R is between points P & Q if and only if R, P, and Q are collinear and PR + RQ = PQ Parts add up to be the whole.

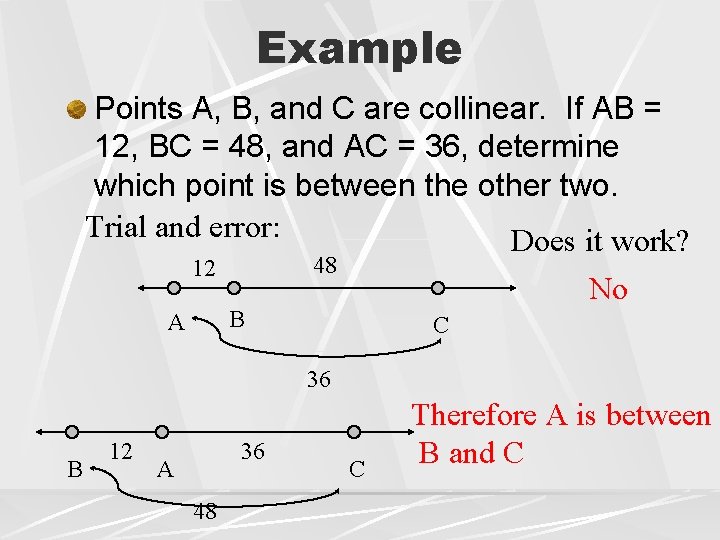
Example Points A, B, and C are collinear. If AB = 12, BC = 48, and AC = 36, determine which point is between the other two. Trial and error: Does it work? 48 12 No B A C 36 B 12 36 A 48 C Therefore A is between B and C

Example Points R, S, and T are collinear. If RS = 42, ST = 17 and RT = 25 determine which point is between the other two. T is between R and S

Equation A statement that includes the symbol = Shows that 2 things are of equal value.

Properties of Equality Reflexive a=a Symmetric If a = b, then b = a Transitive If a = b and b = c, then a = c.

Properties Addition / subtraction If a = b then a + c = b + c or a – c = b – c Multiplication / Division If a = b, then a(c) = b(c) or a/c = b/c Substitution 2 equal quantities may be substituted for each other. x = 2(5) x = 10 sub.

Example If QS = 29 and QT = 52, find ST. Find the relationship and write: QT = QS + ST Fill in and solve: 52 = 29 + ST 23 = ST ST = 23

Example If PR = 27 and PT = 73, find RT. PT = PR + RT 73 = 27 + RT 46 = RT If QR = 15 and RS = 28, find QS QS = QR + RS QS = 43 QS = 15 + 28

Measurement: made up of 2 parts l Measure 10 l Unit of measure cm An example of measurement is 10 cm. Unit of measure refers to only the units.

Precision: depends on the smallest unit used to make the measurement Greatest possible error: half of the smallest unit used to make the measurement Percent of error: found by comparing the greatest possible error with the measurement itself.

Precision 5. 7 cm or 57 mm Precision: 1 mm Greatest possible error: 0. 5 mm Percent of error: 0. 5/57 (100%) About 0. 88%

Precision example Precision: 1/16 in smallest unit on ruler Greatest possible error: 1/32 in smallest unit / 2 Percent of error: 1. 39%