Applied Combinatorics 4 th Ed Alan Tucker Section

Applied Combinatorics, 4 th Ed. Alan Tucker Section 1. 2 Isomorphism Prepared by Jo Ellis-Monaghan 1/25/2005 Tucker, Sec. 1. 2 1

Definition of Isomorphism • Two graphs G and are isomorphic if : – There exists a one-to-one correspondence between vertices in G and , such that – There is an edge between a and b in G if and only if there is an edge between the corresponding vertices and in. • The definition for oriented graphs is the same, except the head and tail of each edge of G must correspond to the head and tail in 1/25/2005 Tucker, Sec. 1. 2 . 2

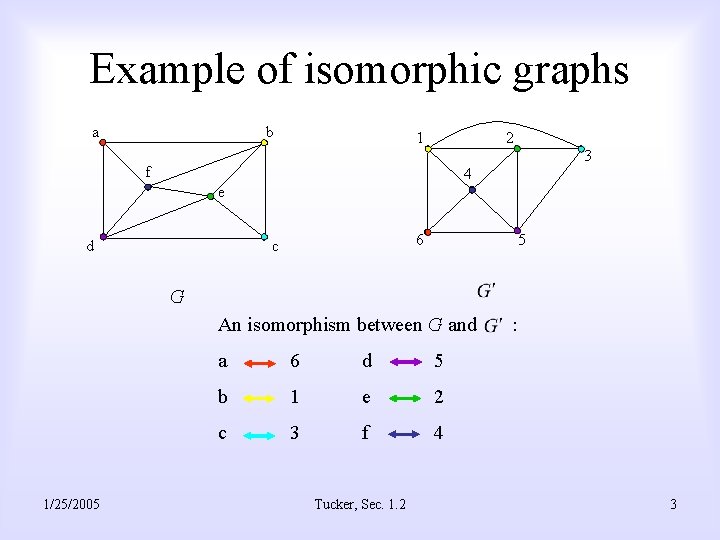
Example of isomorphic graphs a b 1 2 3 f 4 e d 6 c 5 G An isomorphism between G and 1/25/2005 a 6 d 5 b 1 e 2 c 3 f 4 Tucker, Sec. 1. 2 : 3

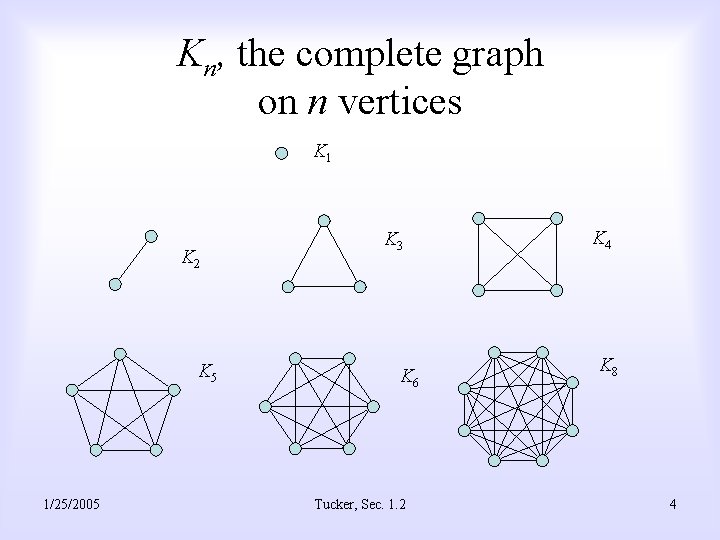
Kn, the complete graph on n vertices K 1 K 2 K 5 1/25/2005 K 3 K 6 Tucker, Sec. 1. 2 K 4 K 8 4

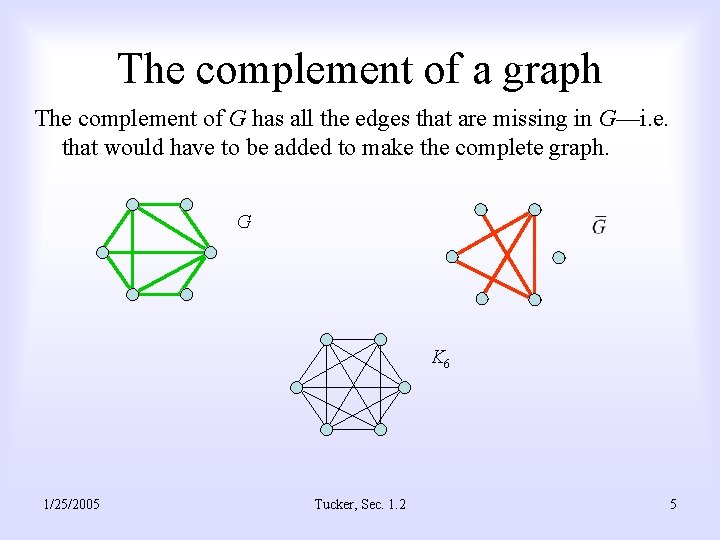
The complement of a graph The complement of G has all the edges that are missing in G—i. e. that would have to be added to make the complete graph. G K 6 1/25/2005 Tucker, Sec. 1. 2 5

Advantage of the complement • Theorem: Two graphs, G and H, are isomorphic if and only if their complements are. In practice this means that we work with whichever of G or has few edges. 1/25/2005 Tucker, Sec. 1. 2 6

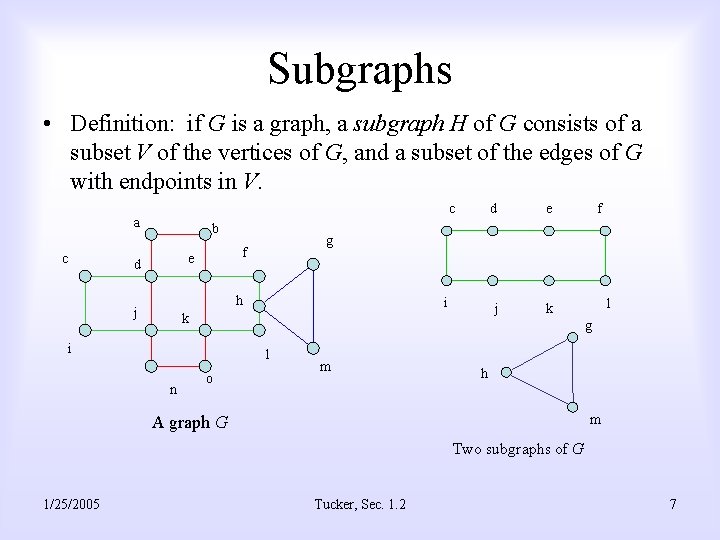
Subgraphs • Definition: if G is a graph, a subgraph H of G consists of a subset V of the vertices of G, and a subset of the edges of G with endpoints in V. c a c b h j i k j k f l g i l n e g f e d d o m h m A graph G Two subgraphs of G 1/25/2005 Tucker, Sec. 1. 2 7

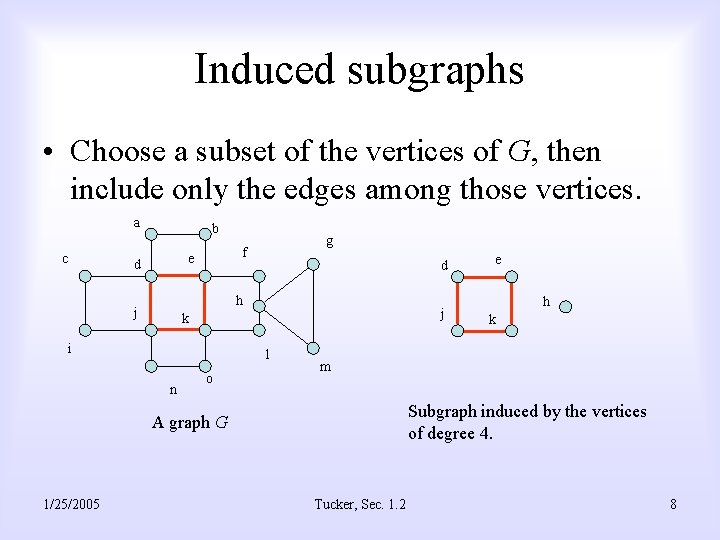
Induced subgraphs • Choose a subset of the vertices of G, then include only the edges among those vertices. a c b e d g f d h j j k i l n o h k m Subgraph induced by the vertices of degree 4. A graph G 1/25/2005 e Tucker, Sec. 1. 2 8

Elementary properties of isomorphic graphs • Edge and vertex counts – Isomorphic graphs have the same number of edges and vertices. • Vertex sequence (the list of vertex degrees) – Isomorphic graphs have the same vertex sequences. • Warning!! These can be used to show two graphs are not isomorphic, but can not show that two graphs are isomorphic. 1/25/2005 Tucker, Sec. 1. 2 9

Two non-isomorphic graphs Vertices: 6 Edges: 7 Vertex sequence: 4, 3, 3, 2, 2, 0. 1/25/2005 Vertices: 6 Edges: 7 Vertex sequence: 5, 3, 2, 2, 1, 1. Tucker, Sec. 1. 2 10

Subgraph properties of isomorphic graphs • Isomorphic graphs have the same sets of subgraphs: – there is a one-to-one correspondence between the subgraphs such that corresponding subgraphs are isomorphic. • Typically check induced subgraphs, or number of a specific kind of subgraphs such as cycles or cliques. • Warning!! These can be used to show two graphs are not isomorphic, but can not show that two graphs are isomorphic. 1/25/2005 Tucker, Sec. 1. 2 11

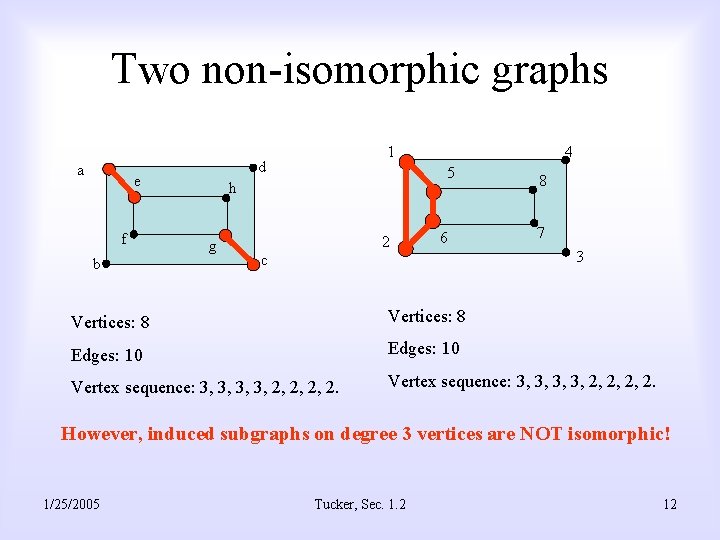
Two non-isomorphic graphs a d e f b 1 5 h g 4 2 6 c 8 7 3 3 Vertices: 8 Edges: 10 Vertex sequence: 3, 3, 2, 2, 2, 2. However, induced subgraphs on degree 3 vertices are NOT isomorphic! 1/25/2005 Tucker, Sec. 1. 2 12

An approach to checking isomorphism: ü Count the vertices. The graphs must have an equal number. ü Count the edges. The graphs must have an equal number. ü Check vertex degree sequence. Each graph must have the same degree sequence. ü Check induced subgraphs for isomorphism. If the subgraphs are not isomorphic, then the larger graphs are not either. üCount numbers of cycles/cliques. If these tests don’t help, and you suspect the graphs actually are isomorphic, then try to find a one-to-one correspondence between vertices of one graph and vertices of the other. Remember that a vertex of degree n in the one graph must correspond to a vertex of degree n in the other. 1/25/2005 Tucker, Sec. 1. 2 13

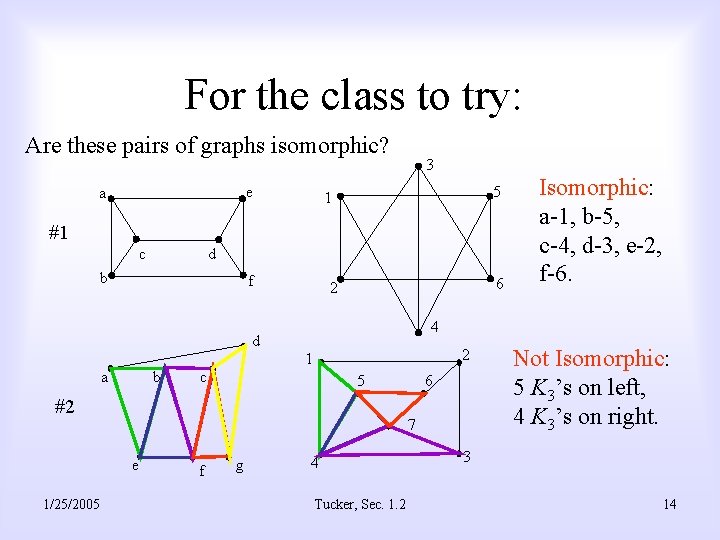
For the class to try: Are these pairs of graphs isomorphic? e a 3 5 1 #1 c d b f d a b 6 2 4 2 1 c 5 #2 1/25/2005 6 7 e f g Isomorphic: a-1, b-5, c-4, d-3, e-2, f-6. 4 Tucker, Sec. 1. 2 Not Isomorphic: 5 K 3’s on left, 4 K 3’s on right. 3 14