Applications of Treewidth in Algorithm Design Daniel Lokshtanov

Applications of Treewidth in Algorithm Design Daniel Lokshtanov Based on joint work with Hans Bodlaender , Fedor Fomin, Eelko Penninkx, Venkatesh Raman, Saket Saurabh and Dimitrios Thilikos

Background Most interesting graph problems are NP-hard on general graphs. Often input graphs are planar or almost planar. Can this be used to give efficient algorithms? Most interesting graph problems remain NPhard on planar graphs.

Are planar graphs as hard as general graphs? On planar graphs many problems admit: - Faster exact algorithms. - Faster parameterized algorithms. - Good preprocessing rules (kernels). - Better approximation algorithms.

Case Study: Dominating Set General Graphs Planar Graphs 1. 49 n 1/2) O(n 2 Parameterized Complexity W[2]-complete 1/2) O(k 2 Kernel W[2]-complete O(k) Approximation log(n) 1+ε Exact Algorithm

Bidimensionality [DFHT] A framework that gives fast exact algorithms, paramterized algorithms, kernels and approximation schemes for problems on planar graphs. Main tool: Graph Minors theory of Robertson and Seymour. Extends to larger classes of graphs. Here; only planar graphs.

Preliminaries

Problems considered Input: G Max / Min: κ(G, S) (S ⊆ V(G) / S ⊆ E(G)) Subject to: φ(G, S) Technical note: we demand that κ(G, S) ≤ |S| and that κ(G, OPT) = |OPT|. Value of optimal solution on G = π(G).

Minors and Contractions H is a minor of G (H ≤m G)if H can be obtained from G by a sequence of edge contractions, edge deletions and vertex deletions. H is a contraction of G (H ≤c G) if H can be obtained from G by a sequence of edge contractions.

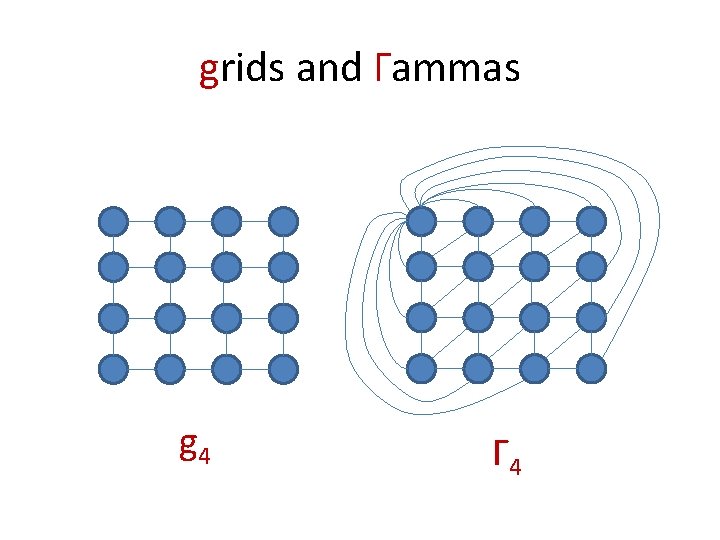
grids and Γammas g 4 Γ 4

Bidimensionality A problem Π is (minor)-bidimensional if: – If H ≤m G then π(H) ≤ π(G). – There is a constant c such that π(gt) ≥ ct 2. A problem Π is contraction-bidimensional if: – If H ≤c G then π(H) ≤ π(G). – There is a constant c such that π(Γt) ≥ ct 2.

Examples of Bidimensional problems • Vertex Cover, Feedback Vertex Set, Longest Path and Cycle Packing are minorbidimensional. • Dominating Set, Connected Vertex Cover and Independent Set are contractionbidimensional.

Facts about Treewidth 1. 2. 3. 4. 5. Many graph probems can be solved in 2 O(tw(G))n time. If H ≤m G then tw(H) ≤ tw(G). The treewidth of gk is k. Every graph G has a balanced separator of size tw(G). On planar graphs, treewidth is constant factor approximable.

Excluded Grid Theorem [RS]: Every planar graph G contains g(1/6)*tw(G) as a minor.

Excluded Γamma Theorem [FGT]: There exists a constant c such that every planar graph G contains Γc*tw(G) as a contraction.

Subexponential Parameterized Algorithms

Parameter-treewidth bound Lemma [Parameter-treewidth bound]: For every bidimensional problem Π there is a constant c such that for any planar graph G, tw(G) ≤ cπ(G)1/2 Proof: By excluded grid theorem, gc*tw(G) ≤m G. Since Π is bidimensional, π(gc*tw(G)) ≥ c’tw(G)2. Since Π is minor closed, π(G) ≥ c’tw(G)2.

Algorithm on planar graphs Constant-factor approximate treewidth. Output a decomposition of width t = O(π(G)1/2). Solve problem in 2 O(t)n (or t. O(t)n) time. Total time 1/2 π(G) taken is 2 n (or π(G) n).

More general graph classes Note: The only place we used planarity was for the excluded grid theorem. So results hold on H-minor-free graphs for minor-bidimensional problems and apex-minor-free graphs for contraction-bidimensional problems.

Exercise 1: Prove: For any fixed d, if G is planar and has a set X such that tw(G X) ≤ d then tw(G) ≤ d + O(|X|1/2). Soln: Vertex deletion into treewidth d graphs is minor closed and at least (t/(d+1))2 on gt grids.

Approximation

Separability Want: EPTASes for all bidimensional problems on planar graphs. (1+ε)-approximation in Parameterf(ε)poly(n) time. Can’t handle Longest Path. treeewidth bound is not enough, but ”almost enough”.

Separability A problem Π is separable* if for any partition of V(G) into L, S, R such that there is no edge from L to R, and optimal solution OPT ⊆ V(G): - π(G R) ≤ κ(G R, OPT R) + O(|S|) - π(G L) ≤ κ(G L, OPT L) + O(|S|) Think ”OPT of left hand side” *For contraction-bidimensional problems a slightly different definition is used.

Excercise 2 Show that Vertex Cover is separable. Solution: OPT R is a feasible solution for G[L ∪ S]. Hence π(G R) ≤ |OPT R|.

Exercise 3: Show that Independent Set is separable. Solution: Let OPT be a maximum independent set of G. Suppose π(G R) > |OPT R| + |S|. Then π(G[L]) > |OPT R| Then G has an independent set of size: π(G[L]) + |OPT ∩ R| > |OPT R| + |OPT ∩ R| =|OPT|.

Decomposition Theorem: For any minor-bidimensional, separable problem Π on planar graphs, there is a function f : N N and polynomial time algorithm that given G and ε > 0 outputs a set X such that - |X| ≤ επ(G) - tw(G X) ≤ f(ε).

Exercise 4: Assume Feedback Vertex Set (FVS) is minorbidimensional, and separable. Give an EPTAS for FVS on planar graphs using the decomposition theorem. Solution: For a fixed ε and given G find X. Solve FVS optimally on G X in g(ε)n time. Add X to the solution. Solution size ≤ (1+ε)π(G).

Decomposition’ Theorem: For any contraction-bidimensional, separable problem Π on planar graphs, there is a function f : N N and polynomial time algorithm that given G and ε > 0 outputs a set X such that - |X| ≤ επ(G) - tw(G X) ≤ f(ε).

Example Dominating Set (DS) is contractionbidimensional, and separable. Thus it has an EPTAS for on planar graphs. Proof: For a fixed ε and given G find X using decomposition’. Mark N(X). Find a smallest set S in GX that dominates all unmarked vertices of GX. Now S ∪ X is a DS of G of size ≤ (1+ε)π(G).

Remainder of talk: Proof Sketch of Decomposition Theorem

Balanced Separator Lemma For any graph G of treewidth t and vertex set X there is a partition of V(G) into L, S, R such that: - There is no edge between L and R - The separator S is small; |S| ≤ t+1. - The separator is balanced; |X ∩ L| ≤ 2|X|/3 and |X ∩ R| ≤ 2|X|/3

Weak, Non-constructive, Decomposition Theorem WNDT: For any minor-bidimensional, separable problem Π on planar graphs, there exists a constant c such that any instance G has a vertex set X such that - |X| ≤ cπ(G) - tw(G X) ≤ c.

WNDT Proof 1. By parameter-treewidth bound, there is a constant d such that tw(G) ≤ dπ(G)1/2. 2. Let T(k) be the smallest number t such that any planar graph G with π(G) = k contains a set X of size t such that tw(G X) ≤ d. 3. Need to prove T(k) = O(k). 4. Base Case: T(1) = 0 since tw(G) ≤ dπ(G)1/2 ≤ d.

WNDT recurrence Let Z be an optimal solution in G, then k=|Z|=π(G). Now, tw(G) ≤ dk 1/2. Balanced Separator Lemma applied to G, Z yields decomposition of V(G) into (L, S, R) such that |S|≤ dk 1/2 , L ∩ Z ≤ 2|Z|/3, R ∩ Z ≤ 2|Z|/3.

WNDT recurrence Since Π is separable: π(G R) ≤ κ(G R, Z R) + O(k 1/2) ≤ |ZR|+ O(k 1/2) GR has a set XL of size T(|ZR|+ O(k 1/2) ) such that tw((GR)XL) ≤ d. GL has a set XR of size T(|ZL|+ O(k 1/2) ) such that tw((GL)XR) ≤ d.

WNDT recurrence X = XL ∪ XR ∪ S is a set of size T(|ZR|+ O(k 1/2) ) + T(|ZL|+ O(k 1/2) ) + O(k 1/2) such that tw(G X) ≤ d. Observe: |ZR| + |ZL| ≤ |Z| + |S|.

WNDT recurrence T(k) ≤ T(�k + O(k 1/2)) + T((1 -�)k + O(k 1/2)) + O(k 1/2). . . where 1/3 ≤ �≤ 2/3. This solves to T(k) = O(k).

Breathe Break Questions?

Scaling Lemma For any c there is a polynomial time algorithm and a function f : N N that given a planar graph G, a set X such that tw(GX) ≤ c, and ε > 0 outputs a set X’ of size ε|X| such that for any component C of G X’ - |C ∩ X| ≤ f(ε) - |N(C)| ≤ f(ε) Implies tw(G[C]) ≤ f’(ε)

Proof Idea for Scaling Lemma For a fixed γ let Tγ(k) be the smallest integer t such that any G with X such that |X|≤ k and tw(GX) ≤ d contains a set X’ of size ≤ t such that for any component C of G X’ - |C ∩ X| ≤ γ - |N(C)| ≤ γ

Proof Idea for Scaling Lemma For every γ > d prove that Tγ(k) ≤ g(γ)k where g(γ) 0 as γ ∞. Prove Tγ(k) ≤ g(γ)k using balanced separation as in the proof of WNDL.

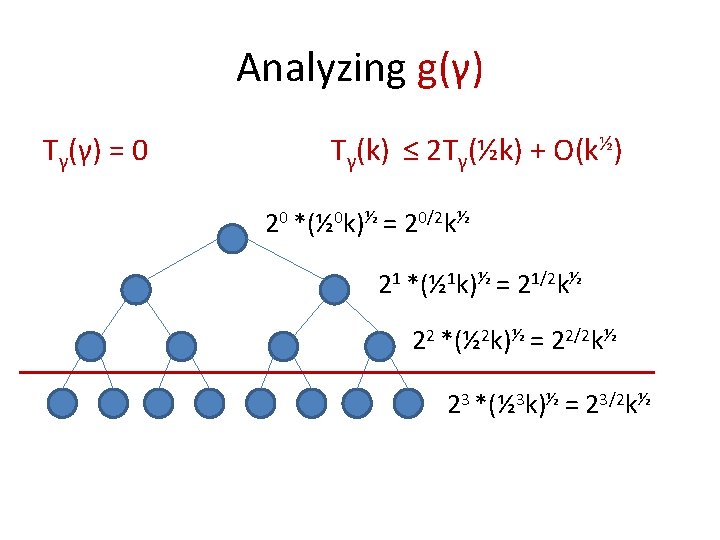
Recurrence for Scaling Lemma Tγ(γ) = 0 See board Tγ(k) ≤ Tγ(�k + O(k 1/2)) + Tγ((1 -�)k + O(k 1/2)) + O(k 1/2). . . where 1/3 ≤ �≤ 2/3. Thus Tγ(k) ≤ g(γ)k but what is lim g(γ) when γ ∞?

Analyzing g(γ) cheat: set �= ½ and move lower order terms outside function calls. Tγ(γ) = 0 Tγ(k) ≤ 2 Tγ(½k) + O(k½)

Analyzing g(γ) Tγ(γ) = 0 Tγ(k) ≤ 2 Tγ(½k) + O(k½) 20 *(½ 0 k)½ = 20/2 k½ 21 *(½ 1 k)½ = 21/2 k½ 22 *(½ 2 k)½ = 22/2 k½ 23 *(½ 3 k)½ = 23/2 k½

Making Proof of Scaling Lemma constructive Proof naturally makes a divide and conquer algorithm for constructing X’ from G, X and ε.

Making Proof of Scaling Lemma constructive Proof naturally makes a divide and conquer algorithm for constructing X’ from G, X and ε.

What we have, what we want Have: Weak Nonconstructive Decomposition Theorem and Scaling Lemma If we could make WNDT constructive, we would be done! Want: Constant factor approximation of ”treewidth-d deletion” on H-minor free graphs.

Protrusion Lemma For every d, there are constants c such that for protrusion: appendage, bagginess, blob, bump, every planar graph G, if tw(G)>d then there is a bunch, bunching, convexity, dilation, distention, vertex set C such that: excess, excrescence, gibbosity, growth, hump, – d < tw(G[C]) ≤ c intumescence, jut, lump, nodulation, nodule, – N(C) ≤ c outgrowth, outthrust, projection, prominence, promontory, protuberance, sac, sagging, salience, Proof: X be smallest set such that tw(G)<d. salient, Let superfluity, swelling, tuberosity, Apply Scaling Lemma tumefaction, tumor, warton X with ε=½. Set c=f(½). Since X’ < X some component C of GX’ has tw(G[C]) > d.

Approximation algorithm for Treewidth-d deletion Let c be as in Protrusion Lemma. While tw(G) > d: Find a vertex set C such that d < tw(G[C]) ≤ c and N(C) ≤ c. Find best treewidth-d-deletion XC in G[C]. Add Xc and N(C) to X. G G (C ∪ N(C)) Output X

Approximation Ratio We deleted X 1, X 2, X 3. . Xt ≤ OPT N(C 1), N(C 2). . . N(Ct) ≤ ct Each Ci contains a vertex from OPT so t ≤ |OPT|. Hence |X| ≤ (c+1)|OPT|

Proof of Decomposition Theorem By WNDT there exists a treewidth d-deletion of size O(π(G)). By approximation we can find a treewidth d-deletion X of size O(π(G)). By Scaling Lemma we can turn X into a treewidth - f(ε) deletion set X’ of size ε|X|. Choosing ε small enough we get |X’| ≤ επ(G).

Approximation - recap Saw a decomposition lemma for bidiemsional, separable problems on H-minor-free graphs and how it can be used to give EPTAS’es for many problems on H-minor free graphs

Kernelization The decomposition lemma can be modified as follows: Lemma: For any minor-bidimensional, separable problem Π on H-minor-free graphs, there is a constant c and polynomial time algorithm that given G outputs a set X such that |X| ≤ cπ(X) and GX can be partitioned into C 1, C 2, . . . Ct where t ≤ cπ(X) such that - there are no edges between Ci and Cj - tw(G[Ci]) ≤ c - tw(G[Cj]) ≤ c

Kernelization Each Ci can be replaced with a constant size graph using techniques from [BFLPST 09]. Kernels of size O(π(G)).

Very Short Summary Bidimensionality is a framework for giving subexponential time algorithms, EPTAS’es and kernels, based on excluded grid theorems and balanced separation techniques.

Thank You!