Applications of the Xray diffraction methods Qualitative and

Applications of the X-ray diffraction methods Ø Qualitative and quantitative phase analysis Ø Crystal structure determination è è Determination of the crystal class Precise measurement of the lattice parameters Volume of the unit cell Atomic positions within the unit cell (chemistry, density and volume of the unit cell) è Determination of the space group è Refinement of the fraction coordinates of atoms è Formulation and refinement of the structure model 1

Applications of the X-ray diffraction methods Analysis of the real structure of matters For a known crystal structure, i. e. , for a known crystal class, space group and fractional coordinates, deviations from the ideal structure are investigated as function of Ø Ø Ø Temperature, Composition, External pressure, Electric or magnetic field, Mechanical loading … 2

Applications of the X-ray diffraction methods Ø Analysis of the real structure of matters – Determination of the lattice parameters § Dependence on temperature phase transitions, anisotropic coefficients of thermal expansion § Dependence on composition e. g. Vegard’s rule in solid solutions § Dependence on pressure phase transitions, change in the atomic structure (impact on electronic structure) § Dependence on electric or magnetic fields information on changes in the electronic structure 3

Applications of the X-ray diffraction methods Ø Analysis of the real structure of matters – Determination of fractional coordinates and lattice vibrations § Dependence on temperature measurement of the Debye temperature, investigation of spontaneous magnetostriction (in own magnetic field) § Dependence on composition formation of ordered structures or superstructures in solid solutions § Dependence on pressure change of interatomic distances (changes in electronic structure) § Dependence on electric or magnetic fields information on changes in electronic structure 4

Applications of the X-ray diffraction methods Ø Analysis of real structure of matters – Crystallite size – Preferred orientation of crystallites (texture) – Kind and density microstructure defects (point defects, dislocations, planar defects, …) – Macroscopic strains – Information about low dimensional structures (surfaces, interfaces, layered systems) 5

Determination of the crystal structure Ø For single crystals if possible Ø Intensity measurement on individual reciprocal lattice points Ø No overlap of the diffraction lines Ø When a single crystal is not available powder diffraction Ø Powder diffraction can only distinguish between lattice planes with different interplanar distances 6

Determination of the crystal structure Crystal class and lattice parameters Ø Indexing of the diffraction lines Experiment: Theory: Least-squares method: h, k, ℓ … Miller indices (integers) a*, b*, c*, *, * … reciprocal lattice parameters 7

Indexing of the diffraction lines DICVOL, PREDICT – D. Louër and A. Boultif ITO – J. Visser TREOR – P. -E. Werner ftp: //ftp. icdd. com/Pre. DICT. zip Blanton, J. , Papoular, R. , & Louër, D. (2019). Pre. DICT: A graphical user interface to the DICVOL 14 indexing software program for powder diffraction data. Powder Diffraction, 34(3), 233 -241. [DOI: 10. 1017/S 0885715619000514] Boultif, A. and Louër, D. (2004). “Powder pattern indexing with the dichotomy method. ” J. Appl. Crystallogr. 37, 724 -731. [DOI: 10. 1107/S 0021889804014876] Louër, D. and Louër, M. (1972). “Méthode d’essais et erreurs pour l’indexation automatique des diagrammes de poudre. ” J. Appl. Crystallogr. 5, 271 -275. [DOI: 10. 1107/S 0021889872009483] 8

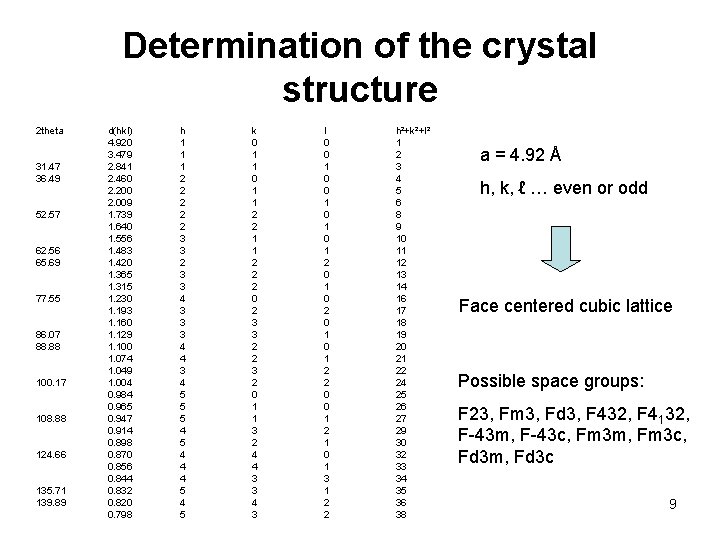
Determination of the crystal structure 2 theta 31. 47 36. 49 52. 57 62. 56 65. 69 77. 55 86. 07 88. 88 100. 17 108. 88 124. 66 135. 71 139. 89 d(hkl) 4. 920 3. 479 2. 841 2. 460 2. 200 2. 009 1. 739 1. 640 1. 556 1. 483 1. 420 1. 365 1. 315 1. 230 1. 193 1. 160 1. 129 1. 100 1. 074 1. 049 1. 004 0. 984 0. 965 0. 947 0. 914 0. 898 0. 870 0. 856 0. 844 0. 832 0. 820 0. 798 h 1 1 1 2 2 2 3 3 4 3 3 3 4 4 3 4 5 5 5 4 4 4 5 k 0 1 1 2 2 2 0 2 3 3 2 2 3 2 0 1 1 3 2 4 4 3 3 4 3 l 0 0 1 0 1 2 2 0 0 1 2 1 0 1 3 1 2 2 h²+k²+l² 1 2 3 4 5 6 8 9 10 11 12 13 14 16 17 18 19 20 21 22 24 25 26 27 29 30 32 33 34 35 36 38 a = 4. 92 Å h, k, ℓ … even or odd Face centered cubic lattice Possible space groups: F 23, Fm 3, Fd 3, F 432, F 4132, F-43 m, F-43 c, Fm 3 m, Fm 3 c, Fd 3 m, Fd 3 c 9

Determination of the crystal structure Possible space groups (face-centered lattice): F 23, Fm 3, Fd 3, F 432, F 4132, F-43 m, F-43 c, Fm 3 m, Fm 3 c, Fd 3 m, Fd 3 c Possible space groups (no diamond lattice, no c-glide plane and no additional screw axis): F 23, Fm 3, F 432, F-43 m, Fm 3 m Chemical analysis: UN, 4 molecules per unit cell F 23, Fm 3, F 432, F-43 m, Fm 3 m: Wyckoff positions 4 a (0, 0, 0) and 4 b (½, ½, ½) Usually, the space group with the highest symmetry is selected 10

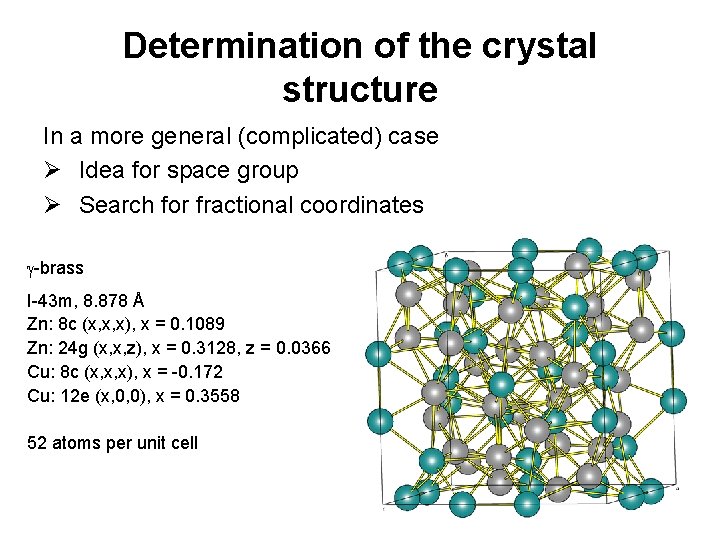
Determination of the crystal structure In a more general (complicated) case Ø Idea for space group Ø Search for fractional coordinates -brass I-43 m, 8. 878 Å Zn: 8 c (x, x, x), x = 0. 1089 Zn: 24 g (x, x, z), x = 0. 3128, z = 0. 0366 Cu: 8 c (x, x, x), x = -0. 172 Cu: 12 e (x, 0, 0), x = 0. 3558 52 atoms per unit cell 11

Determination of the crystal structure Determination of fractional coordinates of atoms (solution of the phase problem) Ø Patterson function Ø Method of a heavy atom Ø Change of atomic scattering factors Ø Direct methods Ø Difference Fourier method 12

Patterson function An autocorrelation function The Patterson function is always centrosymmetric Maxima of the Patterson function represent the distance between two atoms 13

Method of a heavy atom The contribution of an atom to the structure factor depends on the atomic number (i. e. on its atomic mass). A low number of heavy atoms makes the interpretation of the Patterson function easier, because the Patterson pattern contains less maxima. 14

Change of atomic scattering factor Ø Isomorphic substitution of a single atom or atomic type in a chemical process Ø „Physical“ change of the atomic scattering factor (anomalous scattering and anomalous absorption) Near to the absorption edges, f‘ and f‘‘ become highly dependent on the X-ray energy Precondition: measurement with multiple wavelengths use of the synchrotron radiation is required 15

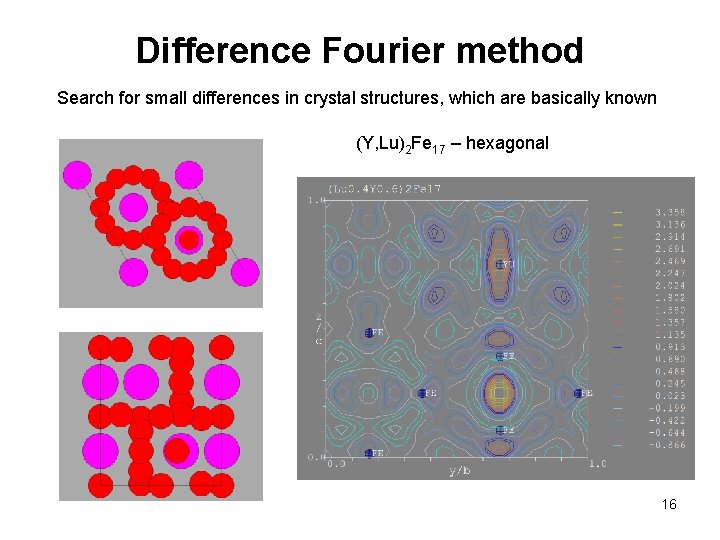
Difference Fourier method Search for small differences in crystal structures, which are basically known (Y, Lu)2 Fe 17 – hexagonal 16