Applications of Symbolic Logic to Gene Regulation Systems

Applications of Symbolic Logic to Gene Regulation Systems Speaker : Chuang-Chieh Lin Department of Computer Science and Information Engineering of National Chung-Cheng University 1

Introduction to Myself Chuang-Chieh Lin 林莊傑 Ø Education Background Ø B. S. Department of Mathematics, National Cheng-Kung University, September 1998 – June 2002. l M. S. Department of Computer Science and Information Engineering, National Chi-Nan University, September 2002 – June 2004. Ø Advisor (2002 – 2004) l Professor R. C. T. Lee l Ø Research l Biocomputing • Sequence Assembly • Evolutionary Trees • Gene Networks <recently> l l Computational Geometry Other topics in the field of Computer Algorithms Computation Theory Laboratory in National Chung-Cheng University 2

Outline Ø Introduction and Motivations Ø Symbolic Logic and the Resolution-Principle Method Ø Boolean Gene Regulatory Network Ø The State Determination Problem Ø The Implicit Interaction Finding Problem Ø Previous Work Ø Future Work Computation Theory Laboratory in National Chung-Cheng University 3

Introduction and Motivations Ø Genes are known as specific regions on a DNA sequence, and they carry information for manufacturing proteins. Ø A genome is all the DNA in an organism, including its genes. Ø DNA is made up of four similar chemicals (called bases and abbreviated A, T, C, and G) that are repeated millions or billions of times throughout a genome. The human genome has 3 billion pairs of bases. Computation Theory Laboratory in National Chung-Cheng University 4

Ø Human genome sequencing was the most important target of Human Genome Project (HGP) which begun formally in 1990. Ø However, after the human genome sequencing was completed, the postgenomic era and the age of functional genomics have arrived. Ø One aspect of functional genomics is the understanding of how genes are expressed or regulated which is critically important to finding ways to fight diseases. Ø It has been found by scientists that diseases are often related to how genes are expressed and regulated. Computation Theory Laboratory in National Chung-Cheng University 5

Ø To study genes, we have to understand gene expressions, which are the processes that hereditary information of genes transforms into m. RNA or proteins. We also can call the gene expression of a gene “state”. Ø We say that a gene is activated if its process of making m. RNA or a protein is executed ; otherwise, we say that a gene is inhibited. Hereafter, we say that the gene expression or the state of a gene A denotes whether A is activated or inhibited. Computation Theory Laboratory in National Chung-Cheng University 6

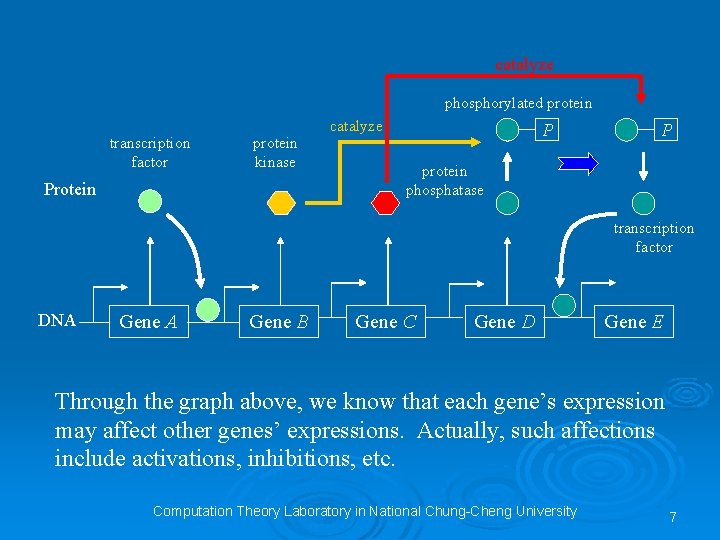
catalyze phosphorylated protein transcription factor protein kinase Protein catalyze P P protein phosphatase transcription factor DNA Gene B Gene C Gene D Gene E Through the graph above, we know that each gene’s expression may affect other genes’ expressions. Actually, such affections include activations, inhibitions, etc. Computation Theory Laboratory in National Chung-Cheng University 7

Ø Suppose we have “gene A activates gene B”, we obtain if gene A is activated, gene B will be activated and if gene A is not activated, gene B won’t be activated. A Ø activate B Similarly, we can obtain that if gene A is activated, gene B will be inhibited and if gene A is not activated, gene B will be activated from “gene A inhibits gene B”. A inhibit B Computation Theory Laboratory in National Chung-Cheng University 8

Ø We say that “A is inhibited” is the same as “A is not activated”, and “A is activated” is the same as “A is not inhibited”. Ø Hence, we may consider the interactions and gene expressions as formulas in symbolic logic. Ø Now, let us go to get familiar with symbolic logic first. Computation Theory Laboratory in National Chung-Cheng University 9

Symbolic Logic Ø For symbolic logic, the symbols, such as A, B and C, are called atoms. Ø Formulas are defined recursively as follows: l l An atom is a formula. If G is a formula, then G is also a formula. If G and H are formulas, then G H, G H and G H are formulas, where , , and dente “or”, “and”, “imply” and “if and only if ” respectively. All formulas are generated by applying the above three rules. Computation Theory Laboratory in National Chung-Cheng University 10

Ø For example, l l l “A”, “B”, “C” are all formulas. “A B” and “B C” are both formulas. “ (A B)” and “ (A B) B C” are both formulas. Computation Theory Laboratory in National Chung-Cheng University 11

Ø We define that an atom or the negation of an atom is a literal. For example, A, B, C are all literals. Ø Suppose we have formulas F 1, F 2, …, Fn, then F 1 F 2 … Fn is called the disjunction of F 1, F 2, …, Fn while F 1 F 2 … Fn is called the conjunction of F 1, F 2, …, Fn. Computation Theory Laboratory in National Chung-Cheng University 12

Ø A disjunction of literals is called a clause. For example, A B, X Y Z are both clauses. Ø A formula F is said to be in a conjunctive normal form if and only if F has the form F 1 F 2 … Fn , n 1, where each Fi is a clause, i = 1, 2, …, n. For example, (A B C) (P Q R) is a formula in a conjunctive normal form. A ( Q R) is also a formula in a conjunctive normal form. Computation Theory Laboratory in National Chung-Cheng University 13

Ø An interpretation of G is an assignment of truth values to A 1, A 2, …, An in which every Ai, 1 i n, is assigned either T or F, but not both. A formula is said to be valid if and only if it is true under all its interpretations, while a formula is said to be inconsistent if and only if it is false under all its interpretations. Ø For example, “ X Y X” is valid. “ X X” is inconsistent. Computation Theory Laboratory in National Chung-Cheng University 14

Ø Given formulas F 1, F 2, …, Fn and a formula G, G is said to be a logical consequence of F 1, F 2, …, Fn if and only if whenever F 1 F 2 … Fn is true then G is also true. That is, G is a logical consequence of F 1, F 2, …, Fn if and only if the formula (F 1 F 2 … Fn) G is valid. Ø The resolution-principle method is a method for deducing logical consequences from a given set of clauses. We define the resolution principle method as follows. Computation Theory Laboratory in National Chung-Cheng University 15

The Resolution-Principle Method Ø For any two clauses C 1 and C 2, if there is a literal L 1 in C 1 that is complementary to a literal L 2 in C 2, then delete L 1 and L 2 from C 1 and C 2 respectively, and construct the disjunction of the remaining clauses. The constructed clause is a logical consequence of C 1 and C 2. Ø For example, Computation Theory Laboratory in National Chung-Cheng University 16

Ø Through what we have discussed previously, how a gene regulates the other genes may be simply represented in symbolic logic. For example, A A activate inhibit B B Computation Theory Laboratory in National Chung-Cheng University 17

Note that we can also transfer the following case into formulas in symbolic logic. B activ ate D t inhibi at e A it b i h n i inhibit E F ac tiv Ø C Computation Theory Laboratory in National Chung-Cheng University 18

Ø In this thesis, “A” stands for “gene A is activated” while “ A” stands for “gene A is not activated”, that is, “gene A is inhibited”. Ø For “A B”, “A B” and “ A B”, we have the following explanations. l l “A B” means “If A is activated, B will be activated. ” “ A B” means “If A is inhibited, B will be activated. ” “A B” means “If A is activated, B will be inhibited. ” “ A B” means “If A is inhibited, B will be inhibited. ” Computation Theory Laboratory in National Chung-Cheng University 19

Ø Note that A B is equivalent to A B. Similarly, A B is equivalent to A B, A B is equivalent to A B. Ø Next, we are going to introduce a graphic model representing a system of given genes and the regulations between them. Computation Theory Laboratory in National Chung-Cheng University 20

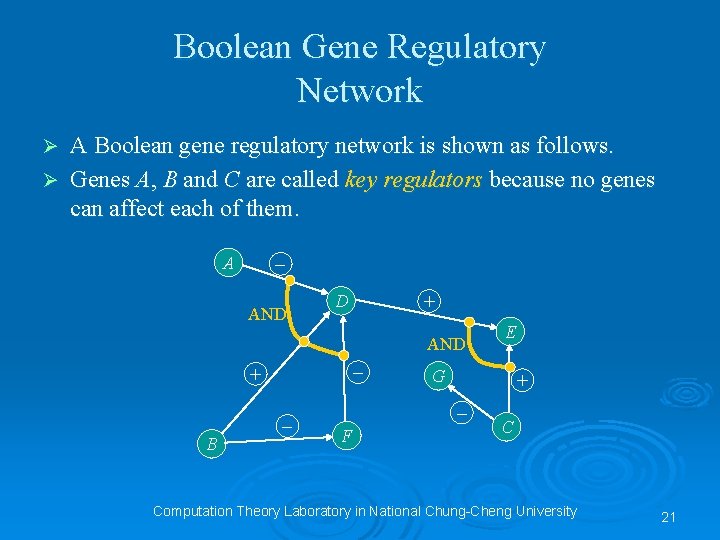
Boolean Gene Regulatory Network A Boolean gene regulatory network is shown as follows. Ø Genes A, B and C are called key regulators because no genes can affect each of them. Ø – A AND + D AND – + B – G + – F E C Computation Theory Laboratory in National Chung-Cheng University 21

Ø Ø After the Boolean gene regulatory network is given, we can consider two problems related to this graph model. l The State Determination Problem l The Implicit Interaction Finding Problem To simplify our discussion, we abbreviate “the Boolean gene regulatory network” to “the Boolean network”. Computation Theory Laboratory in National Chung-Cheng University 22

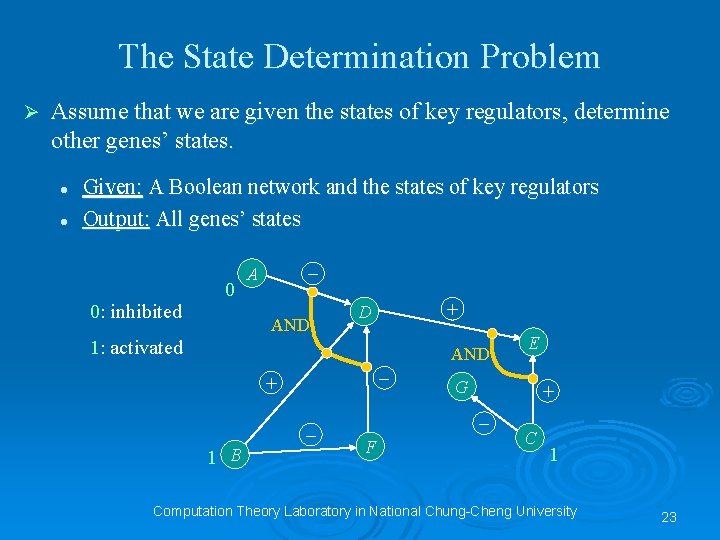
The State Determination Problem Ø Assume that we are given the states of key regulators, determine other genes’ states. l l Given: A Boolean network and the states of key regulators Output: All genes’ states 0: inhibited 0 – A AND + D 1: activated AND – + – 1 B G + – F E C 1 Computation Theory Laboratory in National Chung-Cheng University 23

Ø We can determine all genes’ states, that is, activated or inhibited, by the depth-first-search method or the resolution-principle method. Ø Note that we don’t consider any Boolean network with cycles or self-loops. In addition, the Boolean gates here we use are only AND gates. Computation Theory Laboratory in National Chung-Cheng University 24

Ø By the depth-first-search method: Stage 0: 0 – A AND + D AND – + – 1 B G + – F E C 1 Key regulators: A, B, C Computation Theory Laboratory in National Chung-Cheng University 25

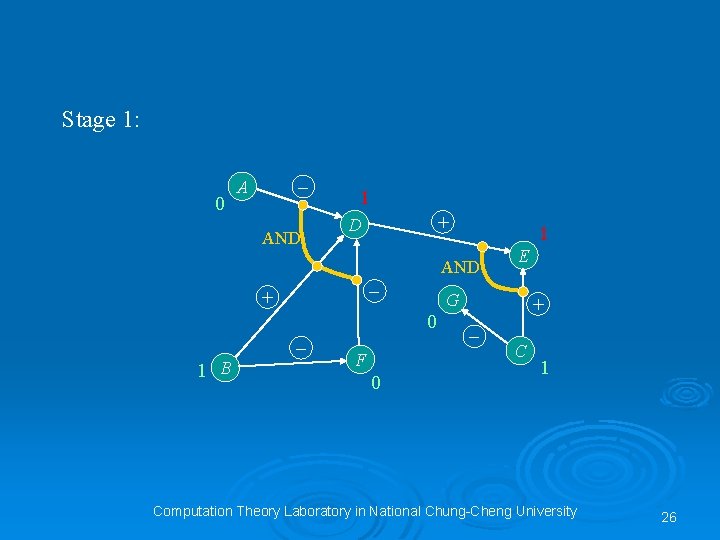
Stage 1: 0 – A AND 1 + D 1 AND – + G 0 – 1 B F 0 E + – C 1 Computation Theory Laboratory in National Chung-Cheng University 26

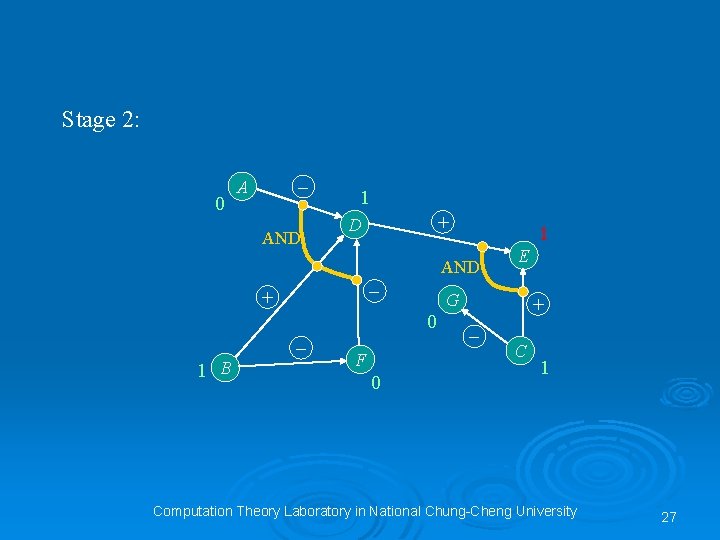
Stage 2: 0 – A AND 1 + D 1 AND – + G 0 – 1 B F 0 E + – C 1 Computation Theory Laboratory in National Chung-Cheng University 27

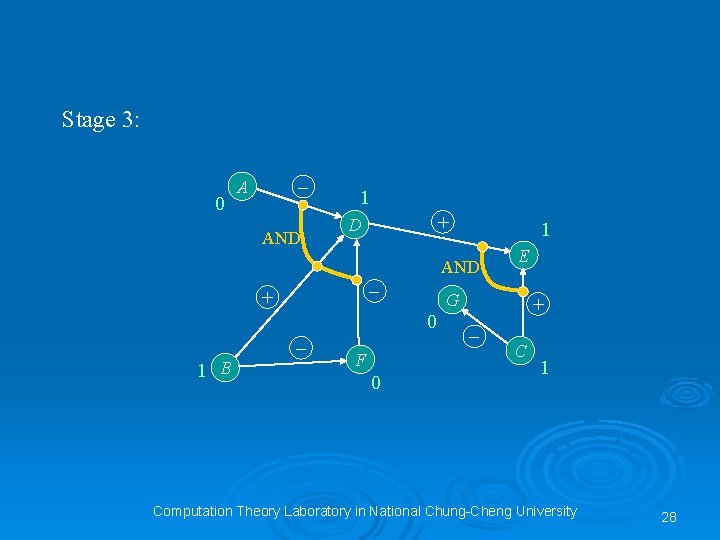
Stage 3: 0 – A AND 1 + D 1 AND – + G 0 – 1 B F 0 E + – C 1 Computation Theory Laboratory in National Chung-Cheng University 28

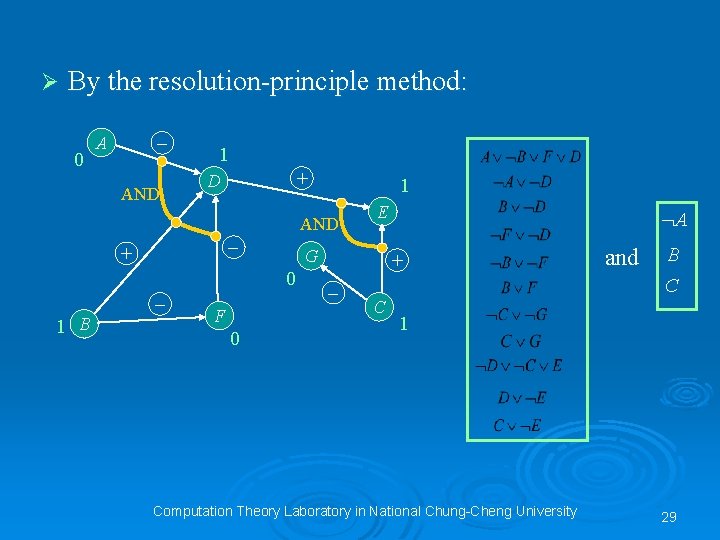
Ø By the resolution-principle method: 0 – A AND 1 + D 1 AND – + G 0 – 1 B F 0 E A + – and B C C 1 Computation Theory Laboratory in National Chung-Cheng University 29

A B C …(1) …(2) …(3) …(4) …(5) …(6) …(7) …(8) …(9) …(10) …(11) Original Boolean network …(12) …(13) …(14) Key regulators Computation Theory Laboratory in National Chung-Cheng University 30

(7)&(14) (1)&(12) (13)&(16) (5)&(13) (17)&(18) (9)&(17) (14)&(20) (18)&(21) G ………………… (15) B F D ………. . . (16) F D ……………. . . (17) F …………. . (18) D …………………. (19) C E F ………. . (20) E F ……………… (21) E ……………. …… (22) Computation Theory Laboratory in National Chung-Cheng University 31

Ø The result can be summarized as follows. A Inhibited B Activated C Activated D Activated E Activated F Inhibited G Inhibited Computation Theory Laboratory in National Chung-Cheng University 32

Ø This problem must be able to be solved based upon Lemma 1 and Theorem 1 as follows. Ø Lemma 1 A Boolean gene regulatory network which is free of cycles and free of self loops has at lease one node whose indegree, that is, the number of other genes that inhibits or activates it directly, is equal to 0. Ø Theorem 1 Assume that a Boolean gene regulatory network G and the states of all key regulators in G are given, then the states of all the nodes G can be all determined. Computation Theory Laboratory in National Chung-Cheng University 33

Ø Lemma 1 and Theorem 1 are easy to be proved. Here we omit the detail of the proofs. Ø Now, let us go to discuss the other problem: the implicit interaction finding problem. Computation Theory Laboratory in National Chung-Cheng University 34

The Implicit Interaction Finding Problem Ø The implicit interaction finding problem is to derive more interactions which are previously unknown from a given Boolean gene regulatory network. l l Given: A Boolean network Output: Implicit interactions in the Boolean network + A – AND D B – + C Computation Theory Laboratory in National Chung-Cheng University 35

(1) (2) + A – AND D (3) B – (4) (5) + (6) (7) C (8) (9) (10) Computation Theory Laboratory in National Chung-Cheng University 36

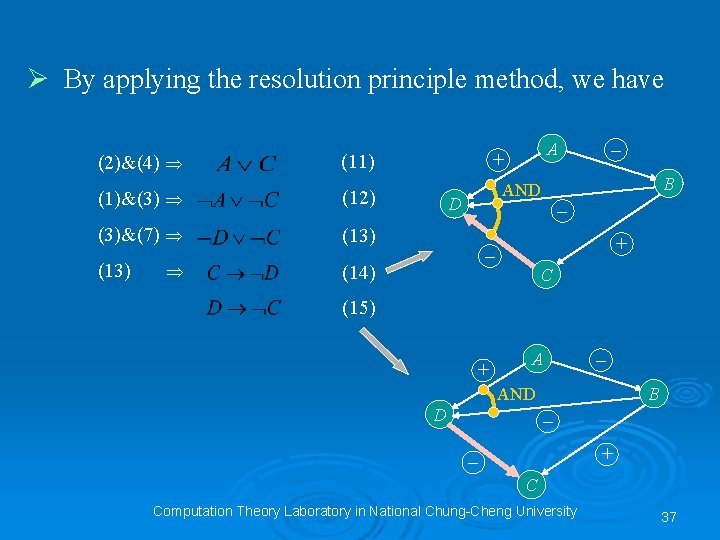
Ø By applying the resolution principle method, we have (2)&(4) (1)&(3) (12) (3)&(7) (13) (14) (13) B AND D – A + (11) – + – C (15) + A – B AND D – + – C Computation Theory Laboratory in National Chung-Cheng University 37

Previous Work Ø In the analysis of gene regulation systems, a lot of results are related to constructing graphic gene regulatory networks. Ø For instance, Andreas Wagner proposed a method to reconstruct a gene regulatory network with core structure from given perturbation data. [W 2001] How to Reconstruct a Large Genetic Network from n Gene Perturbations in fewer than n 2 Easy Steps, Wagner, A. , Bioinformatics, Vol. 17, No. 12, 2001, pp. 11831197. Ø Note that a perturbation is an experimental manipulation performed on a gene. Computation Theory Laboratory in National Chung-Cheng University 38

perturbationlist: Corresponding graph G will be very complicated, so we omit it here. 0: 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 2 16 0 2 5 8 12 14 16 0 2 5 12 14 16 2 8 17 0 0 8 0 0 2 8 1 2 5 6 10 12 14 15 16 18 20 1 2 5 6 12 14 16 18 20 2 14 16 17 2 16 8 0 2 5 6 12 14 16 18 Computation Theory Laboratory in National Chung-Cheng University 39

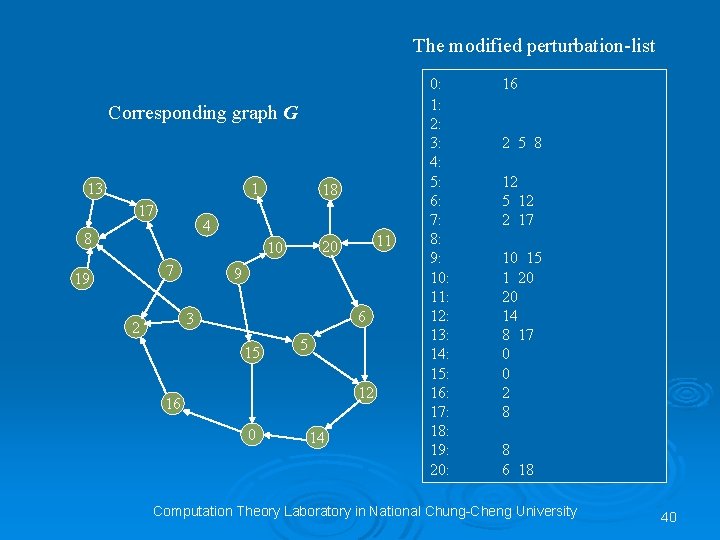
The modified perturbation-list Corresponding graph G 1 13 17 18 4 8 7 19 9 6 3 2 11 20 10 15 5 12 16 0 14 0: 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 16 2 5 8 12 5 12 2 17 10 15 1 20 20 14 8 17 0 0 2 8 8 6 18 Computation Theory Laboratory in National Chung-Cheng University 40

Future Work Ø The identification problem Ø Other topics on biocomputing and computer algorithms Computation Theory Laboratory in National Chung-Cheng University 41

The Identification Problem Ø Given a set of genes and a set of results of perturbations performed on the genes. The identification problem is to determine whethere exists only one Boolean network consistent with the given data. Ø Akutsu et al. have shown that exponential perturbations are needed to identify the unique Boolean network. [AKMM 98] Identification of Gene Regulatory Networks by Strategic Gene Disruptions and Gene Overexpressions, Akutsu, T. , Kuhara, S. , Maruyama, O. and Miyano, S. , Proceedings of the Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, 1998, pp. 695 -702. Computation Theory Laboratory in National Chung-Cheng University 42

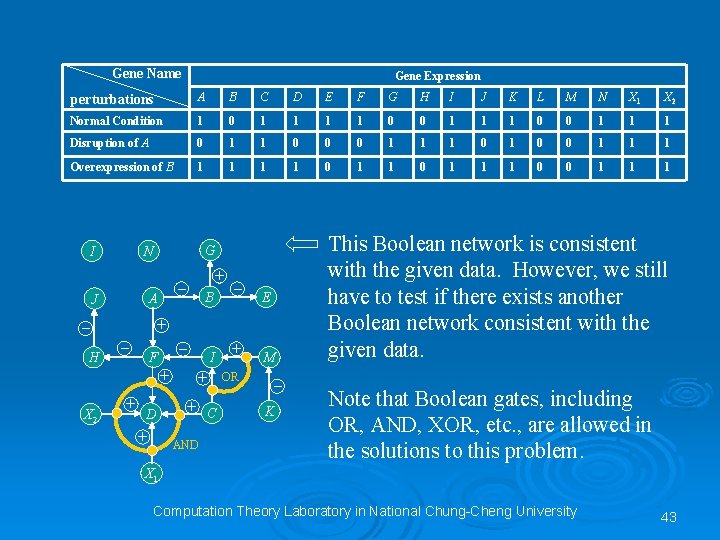
Gene Name Gene Expression perturbations A B C D E F G H I J K L M N X 1 X 2 Normal Condition 1 0 1 1 0 0 1 1 1 Disruption of A 0 1 1 0 0 0 1 1 1 Overexpression of B 1 1 0 1 1 1 0 0 1 1 1 I B – E + – – – F + X 2 + – A J H G N + D + I + + C AND + OR M – K This Boolean network is consistent with the given data. However, we still have to test if there exists another Boolean network consistent with the given data. Note that Boolean gates, including OR, AND, XOR, etc. , are allowed in the solutions to this problem. X 1 Computation Theory Laboratory in National Chung-Cheng University 43

Thank you.