Applications of Sequences and Series Compound interest with

Applications of Sequences and Series. Compound interest with geometric sequence and finance solver.

Compound interest is the addition of interest to the principal sum of a loan or deposit, or in other words, interest on interest. It is the result of reinvesting interest, rather than paying it out, so that interest in the next period is then earned on the principal sum plus previouslyaccumulated interest. What is 'Compound Interest' Compound interest (or compounding interest) is interest calculated on the initial principal and also on the accumulated interest of previous periods of a deposit or loan. Thought to have originated in 17 th-century Italy, compound interest can be thought of as “interest on interest, ” and will make a sum grow at a faster rate than simple interest, which is calculated only on the principal amount. The rate at which compound interest accrues depends on the frequency of compounding; the higher the number of compounding periods, the greater the compound interest. Thus, the amount of compound interest accrued on $100 compounded at 10% annually will be lower than that on $100 compounded at 5% semi-annually over the same time period.

How does it work? Suppose you invest $2000 in the bank. You leave the money in the bank for 4 years, and are paid an interest rate of 5% per annum (p. a). The interest is added to your investment each year, so the total value increases. After one year your investment is worth After two years your investment is worth After three years your investment is worth After four years your investment is worth

After one year After two years After three years After four years Compare to a geometric sequence: initial investment amount after 1 year amount after 2 years amount after 3 years amount after 4 years

In general: where initial investment growth multiplier for each period number of compounding periods amount after n compounding periods

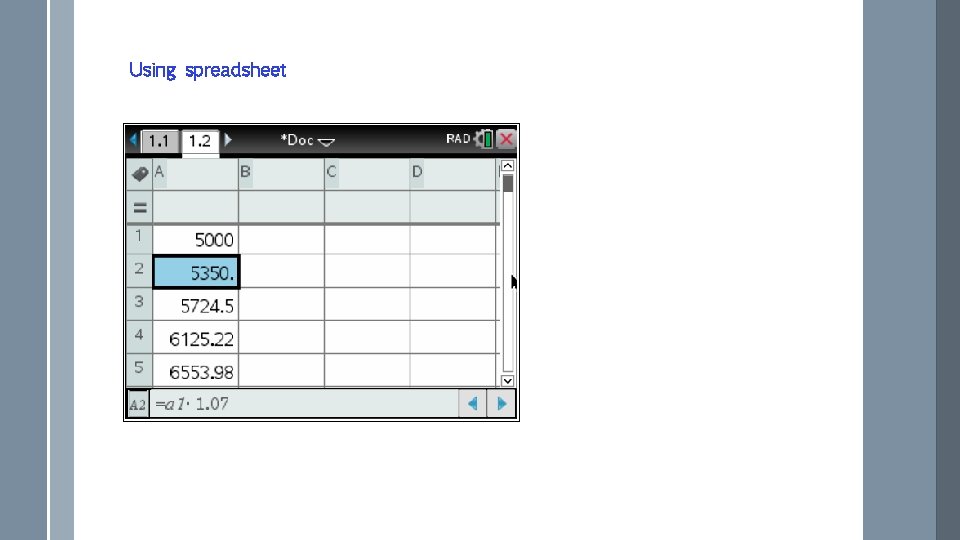
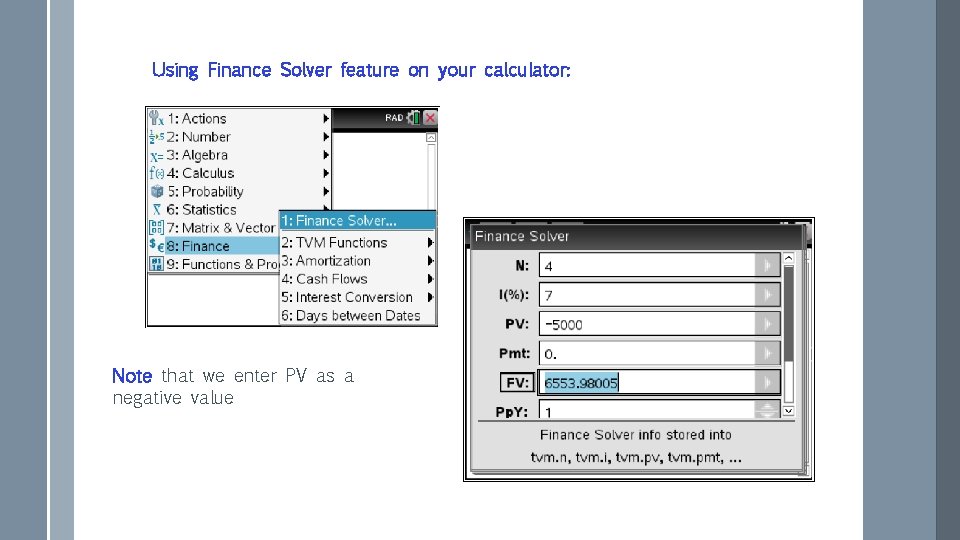
Example: $5000 is invested for 4 years at 3% p. a. compound interest, compounded annually. What will it amount to at the end of this period? Give your answer to the nearest cent. is the amount after 4 years

Using spreadsheet

Using Finance Solver feature on your calculator: Note that we enter PV as a negative value

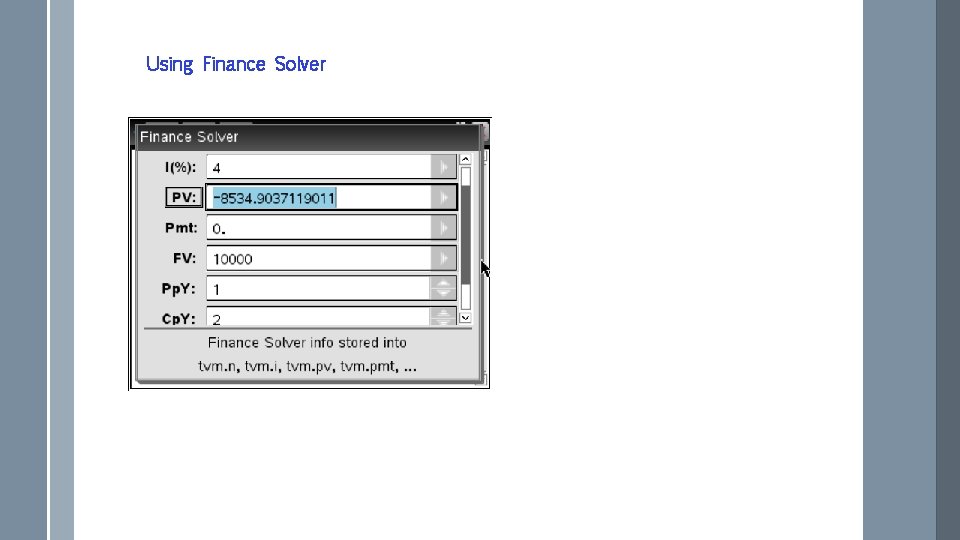
Example. How much should I invest now if I need $10000 in 4 years’ time and I am able to invest at 4% p. a. compounded twice annually. The initial investment is unknown. The investment is compounded twice annually There are 8 compounding periods. Solving gives $8534. 90

Using Finance Solver

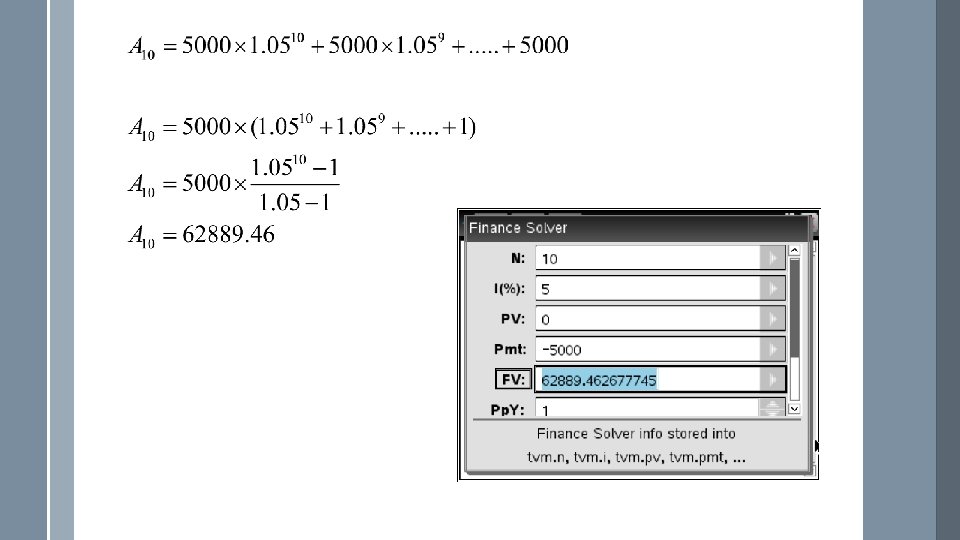
Geometric series with compound interest and additional periodic payments. Example: Each year an investor puts $5000 into the bank account which pays 5% interest p. a. , with interest being paid annually. Find the amount of money the investor has after 10 years. Let An be the amount of money in the account at the end of the nth year, and so on.