Applications of Relative Importance o Why is relative

Applications of Relative Importance o Why is relative importance interesting? n n Web Social Networks Citation Graphs Biological Data o Graphs become too complex for manual analysis

Existing Techniques o Web n Page. Rank (Google) o Social Networks n ‘Centrality’ o All focus on global measures of node importance – we’re interested in importance relative to a set of root nodes R

Use Existing Techniques? o Use global algorithm on the subgraph surrounding root nodes? o No preferential treatment of root nodes – just ranking surrounding nodes.

Organization: Relative importance Algorithms n n Notation Problem Formulation General Framework Algorithms

Notation o Digraph n G = (V, E) o Edges n Ordered pair of nodes (u, v) o Graphs are directed, unweighted, simple o Walks from u to v n n a. k. a. n A walk is a path with no repeated nodes 5

Notation o k-short paths o P(u, v) – set of paths between u and v o – set of distinct out-going edges from u o o Similarly, we have

Problem Formulation 1. Given G and r and t, where , compute the “importance” of t w. r. t. root node r:

Problem Formulation 2. Given G and node vertices in T(G), T , rank all V, w. r. t. r.

Problem Formulation 3. Given G, a set of nodes T(G) to rank, and a set of root nodes R(G) where R V, rank all vertices in T w. r. t. R. This is similar to the last case, except that we compute rather than Average importance:

Problem Formulation (3 cont’d. ) o Rather than average each node’s importance score, we could define o This requires ‘important’ nodes to have a high importance score among all nodes in R

Problem Formulation 4. Given G, rank all nodes where R=T=V.

General Framework: Weighted Paths o Nodes are related according to the paths that connect them o The longer the path, the less importance: is a scalar coefficient, P(r, t) is a set of paths from r to t, pi is the ith path in P. Importance decays exponentially

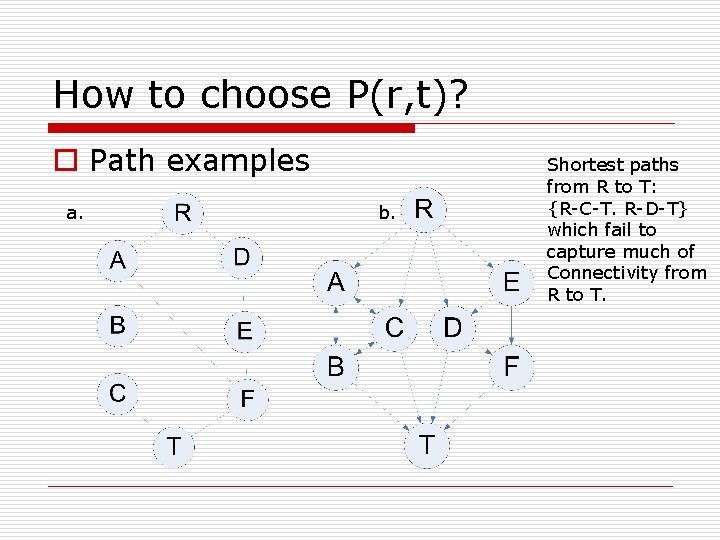
How to choose P(r, t)? o Path examples a. b. Shortest paths from R to T: {R-C-T. R-D-T} which fail to capture much of Connectivity from R to T.

Shortest Path o e. g. : Transport cargo from r to t o Shortest path doesn’t always give a good approximation of importance. n E. g: the web (graph b)

k-Short Paths of length K o Idea: there might often be longer paths than the shortest ones that are important to take into account o Fixes problem of longer, important paths in Shortest Paths n e. g. : graph b. , 3 -short o Problem: capacity constraints n e. g. : network topology

k-Short Node-Disjoint Paths o No nodes and no edges are repeated n Implicitly enforces capacity constraints n Motivated by ‘mass flow’ where importance can ‘flow’ along paths n e. g. : graph b. o Breadth-first with some heuristic, with some K and some

Markov Chains & Relative Importance o Graph viewed as a stochastic process n Explanation of Markov Chains n Token traversing Chain… n Obviously good for modeling the web

Markov Chains & Relative Importance o Markov Centrality n Mean First Passage Time : expected number of steps until first arrival at node t starting at node r : probability that the chain first returns to state t in exactly n steps

Markov Chains & Relative Importance n Bias toward ‘central nodes’ n COMPLEX!! o Time: O(|V|3) (inversion of |V|x|V| transition matrix) o Space: O(|V 2|)

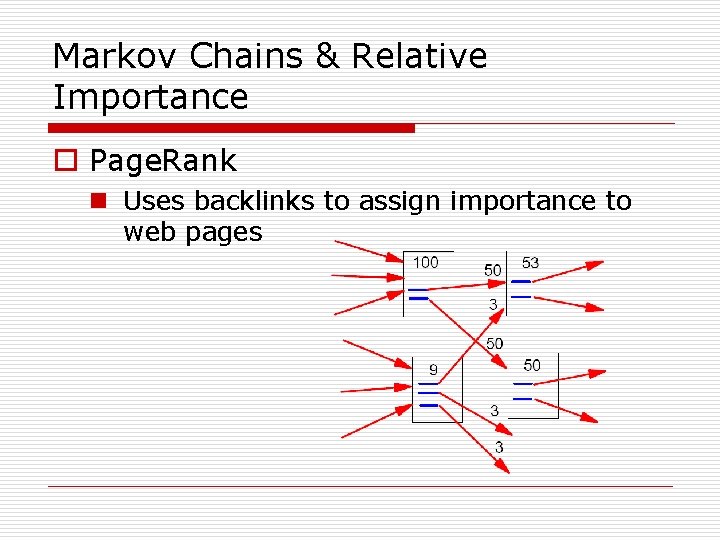
Markov Chains & Relative Importance o Page. Rank n Uses backlinks to assign importance to web pages

Markov Chains & Relative Importance o Page. Rank n Less complex Converges logarithmically n 322 million links processed in 52 iterations

Markov Chains & Relative Importance o Retrofit Page. Rank such that all nodes in R have a uniform bias at the start o ‘Surfer’ begins at a root node, traverses graph, returning to root set R with probability at each time-step o I(t|R) = probability that surfer visits t during a walk

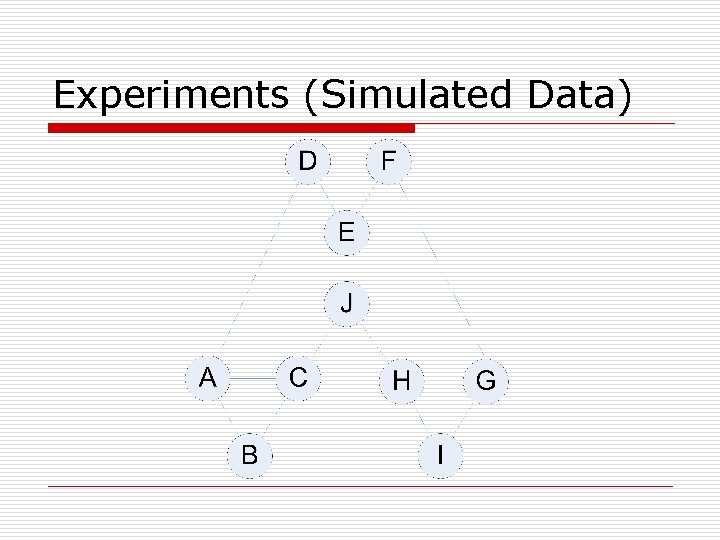
Experiments (Simulated Data)

Experiments (Simulated Data) o More complex n in and out degrees changed n Shortest path lengths between nodes changed (e. g. : A-B) o Analysis which follows, R={A, F} 24

Experiments (Simulated Data) o HITSPa A F G C E H D J I B . 252. 241. 128. 110. 099. 052. 032. 025. 032. 024 o HITSPh F A D B E I H J G C . 225. 186. 162. 119. 090. 067. 061. 050. 028. 008 25

Experiments (Simulated Data) o Markov. C o KSMarkov J C G H E I F D A B . 180. 133. 130. 129. 111. 101. 069. 051. 047. 044 H G E J C I F D A B . 146. 142. 140. 120. 098. 087. 061. 034. 024 26

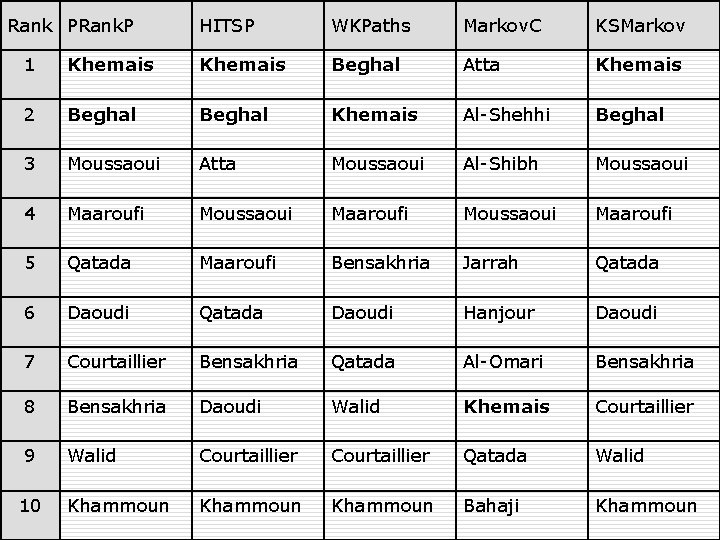
Experiments (9/11 Terrorist Network) o 63 nodes (terrorists) o 308 edges (interactions)

Rank PRank. P HITSP WKPaths Markov. C KSMarkov 1 Khemais Beghal Atta Khemais 2 Beghal Khemais Al-Shehhi Beghal 3 Moussaoui Atta Moussaoui Al-Shibh Moussaoui 4 Maaroufi Moussaoui Maaroufi 5 Qatada Maaroufi Bensakhria Jarrah Qatada 6 Daoudi Qatada Daoudi Hanjour Daoudi 7 Courtaillier Bensakhria Qatada Al-Omari Bensakhria 8 Bensakhria Daoudi Walid Khemais Courtaillier 9 Walid Courtaillier Qatada Walid Khammoun Bahaji Khammoun 10

Conclusion o Provides a first-step to addressing ‘relative-importance’ o Scaling for algorithms such as Markov Chaining can be an issue o Using different algorithms and comparing results can reveal interesting information o …Paper Analysis…

References o White, Smyth. Algorithms for Estimating Relative Importance in Networks. SIGKDD ’ 03. o Page, Brin, Motwani, Winograd. The Page. Rank Citation Ranking: Bringing Order to the Web. Stanford University, Computer Science Department Technical Report. o Wikipedia on Markov Chains n n http: //en. wikipedia. org/wiki/Markov_chain http: //en. wikipedia. org/wiki/Examples_of_Markov_chains