Applications of Metaheuristics to Optimization Problems in Sports

Applications of Metaheuristics to Optimization Problems in Sports Celso C. Ribeiro Joint work with S. Urrutia, A. Duarte, and A. Guedes La Havana, March 2009 8 th International Workshop on Operations Research La Havana, March 2009 Metaheuristics for optimization problems in sports

Summary • Optimization problems in sports – Motivation – How it started: qualification problems – Problems, applications, and solution methods • Applications of metaheuristics – Traveling tournament problem – Referee assignment – Carry-over effect minimization – Brazilian professional basketball tournament • Perspectives and concluding remarks La Havana, March 2009 2 Metaheuristics for optimization problems in sports

Motivation • Sports competitions involve many economic and logistic issues • Multiple decision makers: federations, TV, teams, security authorities, . . . • Conflicting objectives: – Maximize revenue (attractive games in specific days) – Minimize costs (traveled distance) – Maximize athlete performance (time to rest) – Fairness (avoid playing all strong teams in a row) – Avoid conflicts (teams with a history of conflicts La Havana, playing March 2009 at the same Metaheuristics for optimization problems in sports 3 place)

Motivation • Professional sports: – Millions of fans – Multiple agents: organizers, media, fans, players, security forces, . . . – Big investments: • Belgacom TV: € 12 million per year for soccer broadcasting rights • Baseball US: > US$ 500 millions • Basketball US: > US$ 600 millions – Main problems: maximize revenues, optimize logistic, maximize fairness, minimize conflicts La Havana, March 2009 4 Metaheuristics for optimization problems in sports

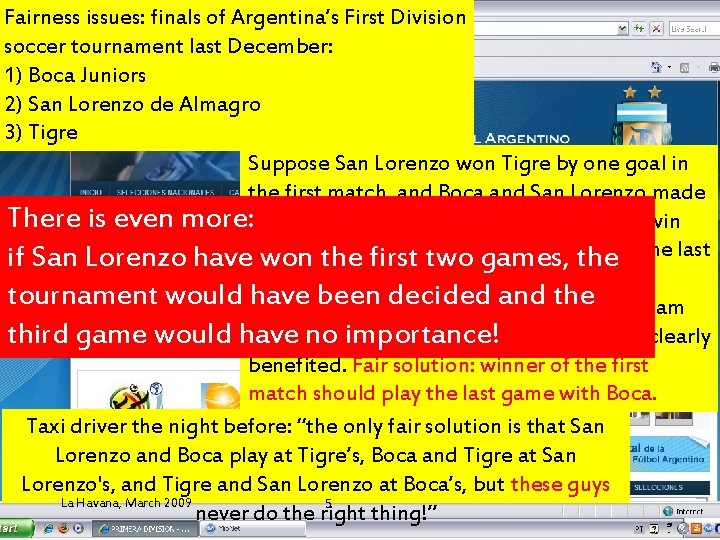
Fairness issues: finals of Argentina’s First Division soccer tournament last December: 1) Boca Juniors 2) San Lorenzo de Almagro 3) Tigre Suppose San Lorenzo won Tigre by one goal in the first match, and Boca and San Lorenzo made There is even more: a tie in the second match. Tigre could not win the first tournament and would play the last if San Lorenzo haveanymore won the two games, the game without motivation and self interest, tournament would maybe have been decided and themain team not even with the complete third game would have importance! (Xmasno vacations. . . ). Boca could have been clearly benefited. Fair solution: winner of the first match should play the last game with Boca. Taxi driver the night before: “the only fair solution is that San Lorenzo and Boca play at Tigre’s, Boca and Tigre at San Lorenzo's, and Tigre and San Lorenzo at Boca’s, but these guys La Havana, March 2009 Metaheuristics for optimization problems in sports 5 never do the right thing!”

Fairness issues: “The International Rugby Board (IRB) has admitted the World Cup draw was unfairly stacked against poorer countries so tournament organisers could maximise their profits. ” (2003) La Havana, March 2009 6 Metaheuristics for optimization problems in sports

Motivation • Amateur sports: – Different problems and applications – Thousands of athletes – Athletes pay for playing – Large number of simultaneous events – Amateur leagues do not involve as much money as professional leagues but, on the other hand, amateur competitions abound La Havana, March 2009 7 Metaheuristics for optimization problems in sports

Optimization problems in sports • Examples: – Qualification/elimination problems – Tournament scheduling – Referee assignment – Tournament planning (teams? dates? rules? ) – League assignment (which teams in each league? ) – Carry-over minimization – Practice assignment –. . . – Optimal strategies for curling! La Havana, March 2009 8 Metaheuristics for optimization problems in sports

Qualification/elimination problems • How all this work it started. . . • Team managers, players, fans and the press are often eager to know the chances of a team to be qualified for the playoffs of a given competition • Press often makes false announcements based on unclear forecasts that are often biased and wrong (“any team with 54 points will qualify”) La Havana, March 2009 9 Metaheuristics for optimization problems in sports

FUTMAX in the WWW FALSE ! La Havana, March 2009 10 Metaheuristics for optimization problems in sports

Qualification/elimination problems • Two basic approaches: click here – Probabilistic model + simulation (abound in the sports press, journalists love but do not understand: “The probability that Estudiantes win is 14, 87%”) – Number of points to qualify: ìnteger programming application, doctorate thesis of Sebastián Urrutia (“easy” only in the last round!) La Havana, March 2009 11 Metaheuristics for optimization problems in sports

Qualification/elimination problems How many points a team should make to: • … be sure of finishing among the p teams in the first positions? (sufficient condition for play-offs qualification) • … have a chance of finishing among the p teams in the first positions? (necessary condition for play-offs qualification): – IP model determines the maximum number K of points a team can make such as that p other teams can make more than K points. – Team must win K+1 points to qualify. La Havana, March 2009 12 Metaheuristics for optimization problems in sports

Qualification/elimination problems • Schwartz 1966: mathematical elimination from play-offs in the Major League Baseball (MLB) solved with maximum flow algorithm • Robinson 1991: IP models and further results for the play-offs elimination problem • Mc. Cormick 2000: elimination from the p-th position is NP-complete. • Bernholt et al. 2002: first place elimination is NP-complete under the {(3, 0), (1, 1)} soccer rule • Adler et al. 2003: ILP models for MLB La Havana, March 2009 13 Metaheuristics for optimization problems in sports

Qualification/elimination problems • Ribeiro & Urrutia 2005: integer programming for qualification/elimination problems in the Brazilian soccer championship and the World Cup (FUTMAX) • Cheng & Steffy 2006: integer programming for qualification/elimination problems in the National Hockey League (spin-off project) La Havana, March 2009 14 Metaheuristics for optimization problems in sports

FUTMAX in the WWW • FUTMAX project • Results of the games automatically collected from the web (multi-agents system): Noronha, Ribeiro, Urrutia & Lucena 2008 • Four IP problems generated for each team • Problems solved with CPLEX 9. 0 • HTML file automatically built from the results • Automatic publication in the web: click here • FUTMAX is often able to prove that statements made by the press and administrators are not La Havana, March 2009 Metaheuristics for optimization problems in sports 15 true

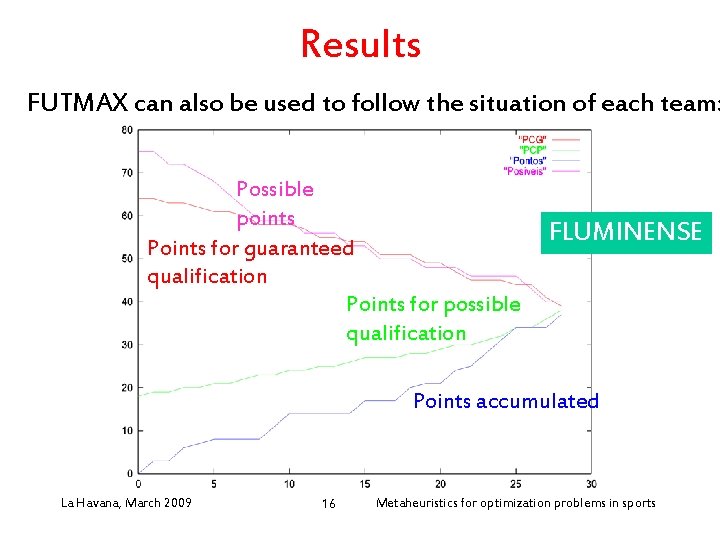
Results FUTMAX can also be used to follow the situation of each team: Possible points Points for guaranteed qualification Points for possible qualification FLUMINENSE Points accumulated La Havana, March 2009 16 Metaheuristics for optimization problems in sports

Tournament scheduling • Timetabling is the major area of applications: game scheduling is a difficult task, involving different types of constraints, logistic issues, multiple objectives, and several decision makers • Round robin schedules: – Every team plays each other a fixed number of times – Every team plays once in each round – Single (SRR) or double (DRR) round robin La Havana, March 2009 17 Metaheuristics for optimization problems in sports

Tournament scheduling • Problems: – Minimize distance (costs) – Minimize breaks (fairness and equilibrium, every two rounds there is a game in the city) – Balanced tournaments (even distribution of fields used by the teams: n teams, n/2 fields, SRR with n 1 games/team, 2 games/team in n/2 -1 fields and 1 in the other) – Minimize carry over effect (maximize fairness, polygon method) La Havana, March 2009 18 Metaheuristics for optimization problems in sports

1 -factorizations • Factor of a graph G=(V, E): subgraph G’=(V, E’) with E’ E • 1 -factor: all nodes have degree equal to 1 • Factorization of G=(V, E): set of edge-disjoint factors G 1=(V, E 1), . . . , Gp=(V, Ep), such that E 1. . . Ep=E • 1 -factorization: factorization into 1 -factors • Oriented factorization: orientations assigned to edges La Havana, March 2009 19 Metaheuristics for optimization problems in sports

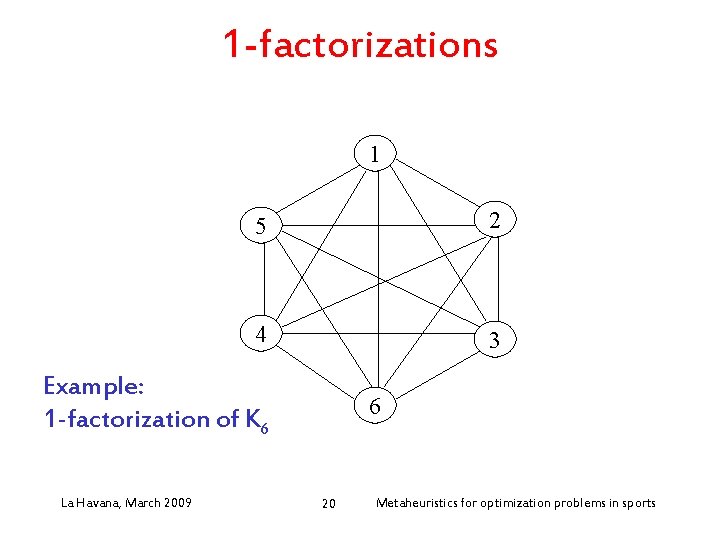
1 -factorizations 1 5 2 4 3 Example: 1 -factorization of K 6 La Havana, March 2009 6 20 Metaheuristics for optimization problems in sports

Oriented 1 -factorization of K 6 1 2 1 3 1 1 5 2 5 2 4 3 4 3 6 6 4 5 1 5 2 4 3 6 La Havana, March 2009 6 1 5 2 4 3 6 21 Metaheuristics for optimization problems in sports

1 -factorizations • SRR tournament: – – Each node of Kn represents a team Each edge of Kn represents a game Each 1 -factor of Kn represents a round Each ordered 1 -factorization of Kn represents a feasible schedule for n teams – Edge orientations define teams playing at home – Dinitz, Garnick & Mc. Kay, “There are 526, 915, 620 nonisomorphic one-factorizations of K 12” (1995) La Havana, March 2009 22 Metaheuristics for optimization problems in sports

Distance minimization problems • Whenever a team plays two consecutive games away, it travels directly from the facility of the first opponent to that of the second • Maximum number of consecutive games away (or at home) is often constrained • Minimize the total distance traveled (or the maximum distance traveled by any team) La Havana, March 2009 23 Metaheuristics for optimization problems in sports

Distance minimization problems • Methods: – Metaheuristics: simulated annealing, iterated local search, hill climbing, tabu search, GRASP, genetic algorithms, ant colonies – Integer programming – Constraint programming – IP/CP column generation – CP with local search La Havana, March 2009 24 Metaheuristics for optimization problems in sports

Break minimization problems • There is a break whenever a team has two consecutive home games (or two consecutive away games) • Break minimization: – De Werra 1981: minimum number of breaks is n -2 • Every team must have a different home-away pattern (they must play in some round) • Only two patterns without breaks: – HAHAHAH. . . – AHAHAHA. . . – Constructive algorithm to obtain schedules with La Havana, exactly March 2009 n-2 breaks 25 Metaheuristics for optimization problems in sports

Break minimization problems • Break minimization is somehow opposed to distance minimization • Urrutia & Ribeiro 2006: a special case of the Traveling Tournament Problem (distance minimization) is equivalent to a break maximization problem La Havana, March 2009 26 Metaheuristics for optimization problems in sports

Predefined timetables/venues • Given a fixed timetable, find a home-away assignment minimizing breaks/distance: – Metaheuristics, constraint programming, integer programming – Miyashiro & Matsui 2005: polynomial method for break minimization if the minimal number of breaks is smaller than or equal to n • Given a fixed venue assignment for each game, find a timetable minimizing breaks/distance: – IP: Melo, Urrutia & Ribeiro 2007 (Jo. S); Costa, (PATAT): ILS problems in sports La Havana, Urrutia March 2009 & Ribeiro 2008 Metaheuristics for optimization 27 metaheuristic

Decomposition methods • Nemhauser & Trick 1998: 1. Find home-away patterns 2. Create an schedule for place holders consistent with a subset of home-away patterns 3. Assign teams to place holders • • Order in which the above tasks are tackled may vary depending on the application Henz 2001: CP may work better than IP and complete enumeration for all the tasks La Havana, March 2009 28 Metaheuristics for optimization problems in sports

Decomposition methods • Frequently used in real-life tournaments: – Nemhauser & Trick 1998: Atlantic Coast Conference (basketball) – Bartsch et al. 2006: Austrian and German soccer – Della Croce & Oliveri 2006: Italian soccer – Ribeiro & Urrutia 2006, 2009: Brazilian soccer – Durán, Noronha, Ribeiro, Sourys & Weintraub 2006: Chilean soccer • Other applications: voleyball in Argentina, soccer in Japan, NHL, basketball in New La Havana, March 2009 Metaheuristics for optimization problems in sports 29 Zealand, etc.

Applications of metaheuristics Traveling Tournament Problem (TTP) and its mirrored version (m. TTP) La Havana, March 2009 30 Metaheuristics for optimization problems in sports

Formulation • Traveling Tournament Problem (TTP) – n (even) teams take part in a tournament – Each team has its own stadium at its home city – Distances between the stadiums are known – A team playing two consecutive away games goes directly from one city to the other, without returning to its home city La Havana, March 2009 31 Metaheuristics for optimization problems in sports

Formulation – Double round-robin tournament: • 2(n-1) rounds, each with n/2 games • Each team plays against every other team twice, one at home and the other away – No team can play more than three games in a home stand (home games) or in a road trip (away games) • Goal: minimize the distance traveled by all teams, to reduce traveling costs and to give more time to the players to rest and practice La Havana, March 2009 32 Metaheuristics for optimization problems in sports

Formulation • Mirrored Traveling Tournament Problem (m. TTP): – All teams face each other once in the first phase (n-1 rounds) – In the second phase (n-1 rounds), teams play each other again in the same order, following an inverted home-away pattern – Games in the second phase determined by those in the first • Set of feasible solutions to the MTTP is a subset of those to the TTP Ribeiro 2004, EJORproblems 2007) La Havana, March 2009& Urrutia (PATAT Metaheuristics for optimization in sports 33

• Constructive heuristic Three steps: 1. Schedule games using abstract teams: polygon method defines the structure of the tournament 2. Assign real teams to abstract teams: greedy heuristic to QAP (number of travels between stadiums of the abstract teams x distances between the stadiums of the real teams) 3. Select stadium for each game (home/away pattern) in the first phase (mirrored tournament): 1. Build a feasible assignment of stadiums, starting from a random assignment in the first round 2. Improve this assignment, using a simple local search algorithm based on home-away swaps La Havana, March 2009 34 Metaheuristics for optimization problems in sports

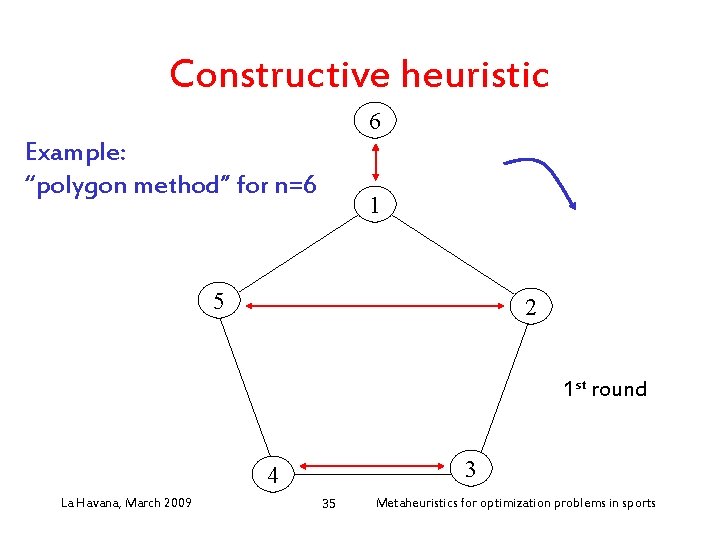
Constructive heuristic 6 Example: “polygon method” for n=6 1 5 2 1 st round 3 4 La Havana, March 2009 35 Metaheuristics for optimization problems in sports

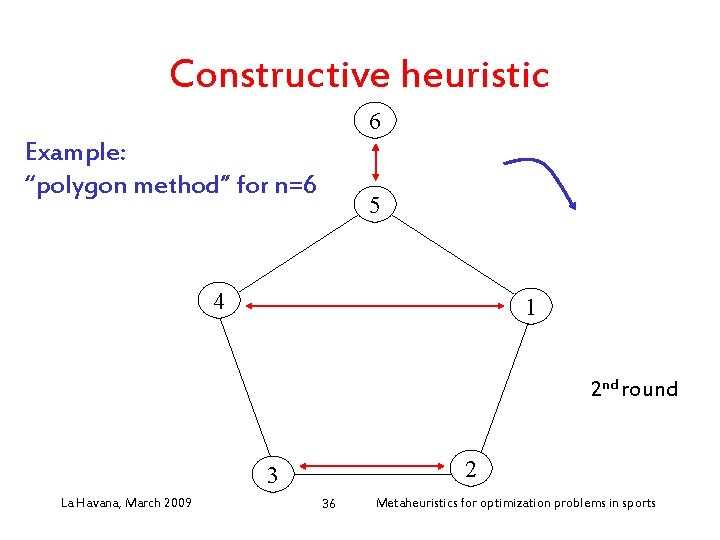
Constructive heuristic 6 Example: “polygon method” for n=6 5 4 1 2 nd round 2 3 La Havana, March 2009 36 Metaheuristics for optimization problems in sports

Simple neighborhoods • Home-away swap (HAS): modify the stadium of a game • Team swap (TS): exchange the sequence of opponents of a pair of teams over all rounds La Havana, March 2009 37 Metaheuristics for optimization problems in sports

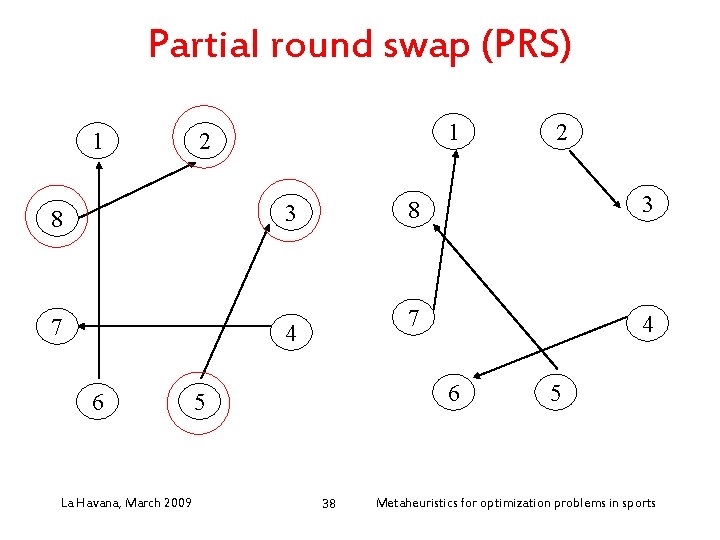
Partial round swap (PRS) 1 1 2 3 8 7 4 6 La Havana, March 2009 8 3 7 4 6 5 38 2 5 Metaheuristics for optimization problems in sports

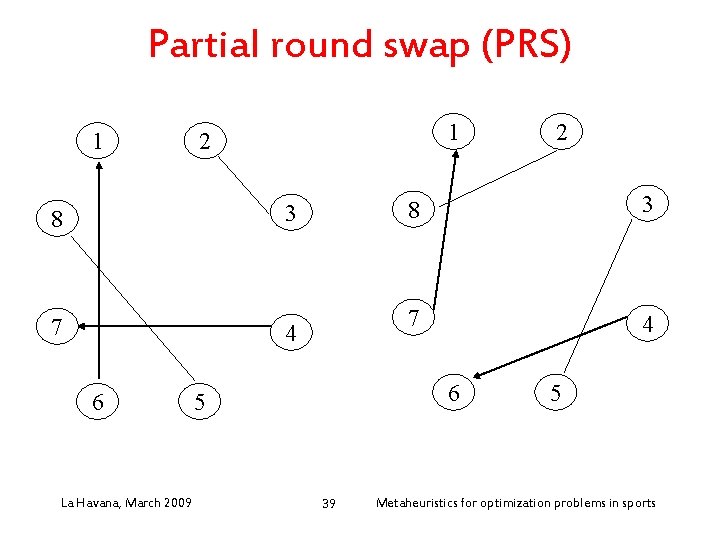
Partial round swap (PRS) 1 1 2 3 8 7 4 6 La Havana, March 2009 8 3 7 4 6 5 39 2 5 Metaheuristics for optimization problems in sports

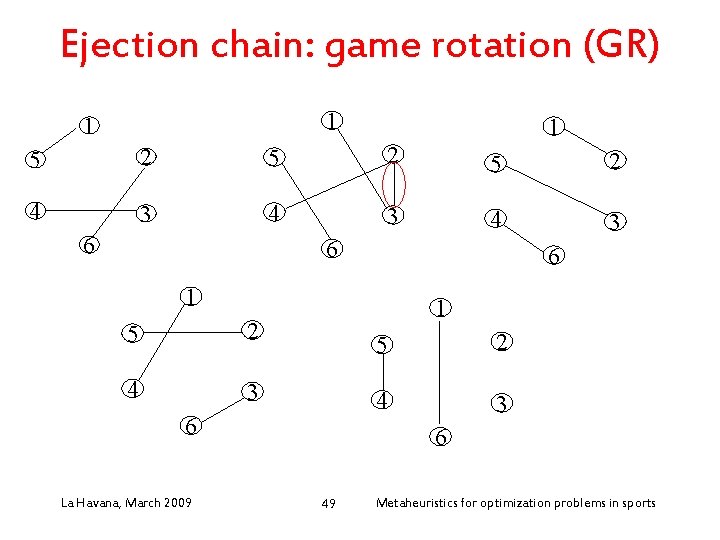
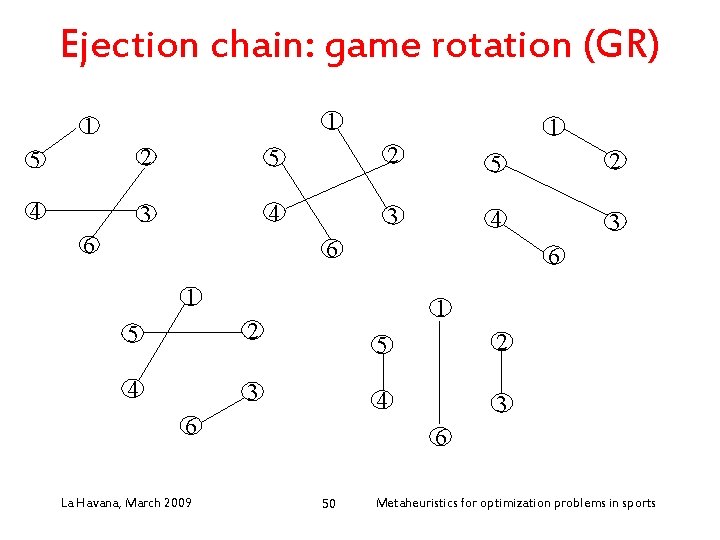
Ejection chain: game rotation (GR) • Neigborhood “game rotation” (GR) (ejection chain): – Enforce a game to be played at some round: add a new edge to a given 1 -factor of the current 1 factorization (schedule) – Use an ejection chain to recover a 1 factorization La Havana, March 2009 40 Metaheuristics for optimization problems in sports

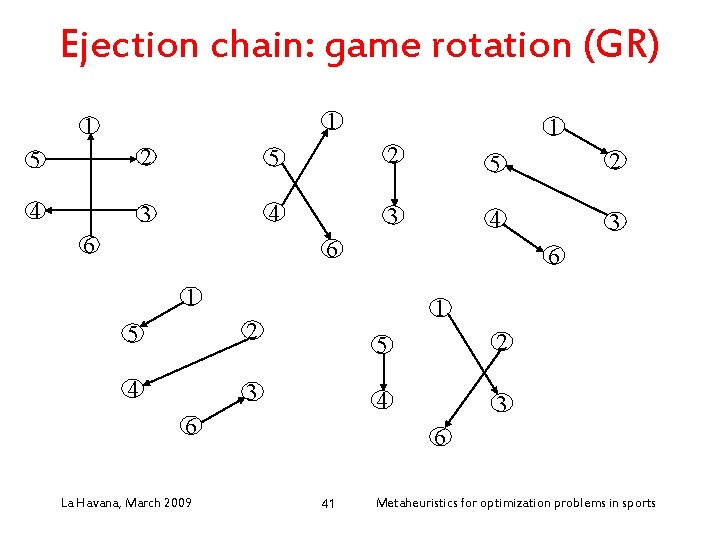
Ejection chain: game rotation (GR) 1 1 1 5 2 5 2 4 3 4 3 6 6 6 1 5 2 4 3 1 6 La Havana, March 2009 5 2 4 3 6 41 Metaheuristics for optimization problems in sports

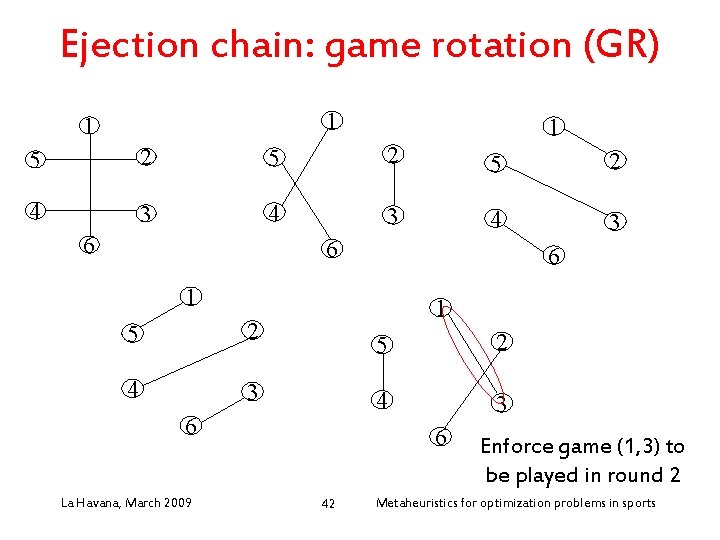
Ejection chain: game rotation (GR) 1 1 1 5 2 5 2 4 3 4 3 6 6 6 1 5 2 4 3 1 6 La Havana, March 2009 5 2 4 3 6 42 Enforce game (1, 3) to be played in round 2 Metaheuristics for optimization problems in sports

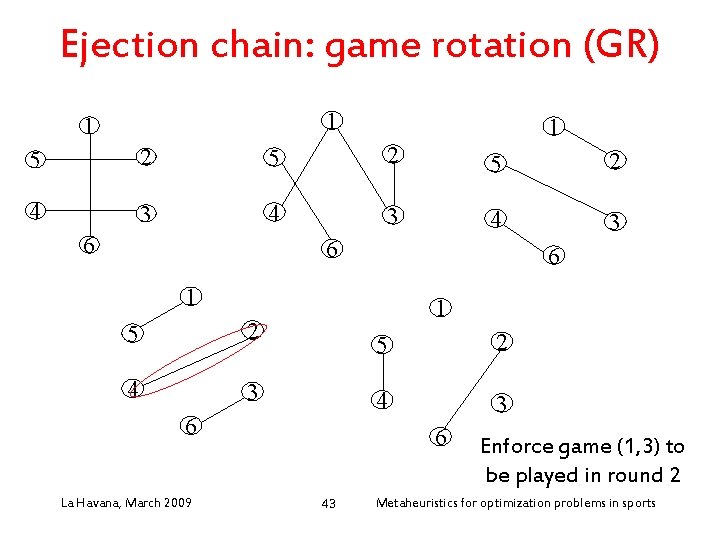
Ejection chain: game rotation (GR) 1 1 1 5 2 5 2 4 3 4 3 6 6 6 1 5 2 4 3 1 6 La Havana, March 2009 5 2 4 3 6 43 Enforce game (1, 3) to be played in round 2 Metaheuristics for optimization problems in sports

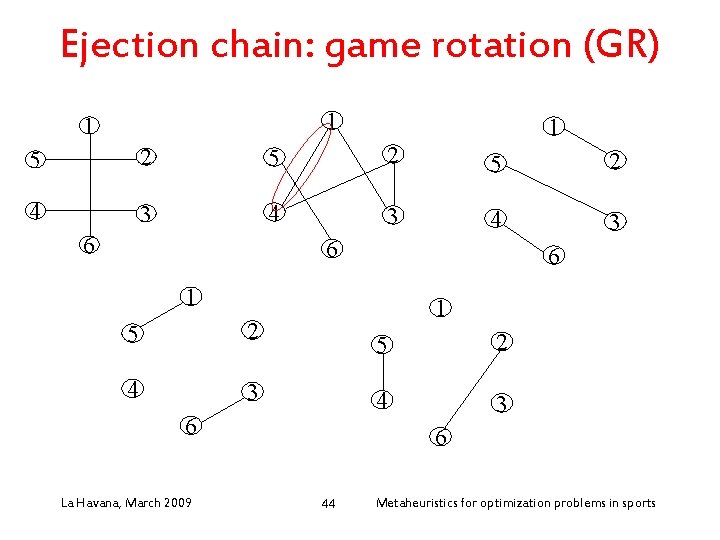
Ejection chain: game rotation (GR) 1 1 1 5 2 5 2 4 3 4 3 6 6 6 1 5 2 4 3 1 6 La Havana, March 2009 5 2 4 3 6 44 Metaheuristics for optimization problems in sports

Ejection chain: game rotation (GR) 1 1 1 5 2 5 2 4 3 4 3 6 6 6 1 5 2 4 3 1 6 La Havana, March 2009 5 2 4 3 6 45 Metaheuristics for optimization problems in sports

Ejection chain: game rotation (GR) 1 1 1 5 2 5 2 4 3 4 3 6 6 6 1 5 2 4 3 1 6 La Havana, March 2009 5 2 4 3 6 46 Metaheuristics for optimization problems in sports

Ejection chain: game rotation (GR) 1 1 1 5 2 5 2 4 3 4 3 6 6 6 1 5 2 4 3 1 6 La Havana, March 2009 5 2 4 3 6 47 Metaheuristics for optimization problems in sports

Ejection chain: game rotation (GR) 1 1 1 5 2 5 2 4 3 4 3 6 6 6 1 5 2 4 3 1 6 La Havana, March 2009 5 2 4 3 6 48 Metaheuristics for optimization problems in sports

Ejection chain: game rotation (GR) 1 1 1 5 2 5 2 4 3 4 3 6 6 6 1 5 2 4 3 1 6 La Havana, March 2009 5 2 4 3 6 49 Metaheuristics for optimization problems in sports

Ejection chain: game rotation (GR) 1 1 1 5 2 5 2 4 3 4 3 6 6 6 1 5 2 4 3 1 6 La Havana, March 2009 5 2 4 3 6 50 Metaheuristics for optimization problems in sports

Neighborhoods • Only moves in neighborhoods PRS and GR may change the structure of the initial schedule • However, PRS moves not always exist, due to the structure of the solutions built by polygon method e. g. for n = 6, 8, 12, 14, 16, 20, 24 • PRS moves may appear after an ejection chain move is made • Ejection chain moves may find solutions that are not reachable through other neighborhoods: escape from local optima La Havana, March 2009 51 Metaheuristics for optimization problems in sports

GRASP+ILS heuristic • Hybrid improvement heuristic for the MTTP: – Combination of GRASP and ILS – Initial solutions: randomized version of the constructive heuristic – Local search with first improving move: use TS, HAS, PRS and HAS cyclically in this order, until a local optimum for all neighborhoods is found – Perturbation: random move in GR neighborhood La Havana, March 2009 52 Metaheuristics for optimization problems in sports

GRASP+ILS heuristic while. not. Stopping. Criterion S Generate. Randomized. Initial. Solution() S Local. Search(S) repeat S’ Perturbation(S, history) S’ Local. Search(S’) S Aceptance. Criterion(S, S’, history) S* Update. Best. Solution(S, S*) until Reinitialization. Criterion end La Havana, March 2009 53 Metaheuristics for optimization problems in sports

Concluding remarks • Constructive heuristic is very fast and effective • GRASP+ILS is very fast and finds very good solutions, even better than the best known for the corresponding (less constrained) not necessarily mirrored instances • Effectiveness of the ejection chains • Theoretical complexity still open La Havana, March 2009 54 Metaheuristics for optimization problems in sports

Applications of metaheuristics Referee Assignment Problem (RAP) La Havana, March 2009 55 Metaheuristics for optimization problems in sports

Motivation • Regional amateur leagues in the US (baseball, basketball, soccer): hundreds of games every weekend in different divisions • In a single league in California there are up to 500 soccer games in a weekend, to be refereed by hundreds of certified referees La Havana, March 2009 56 Metaheuristics for optimization problems in sports

Motivation • MOSA (Monmouth & Ocean Counties Soccer Association) League (NJ): boys & girls, ages 818, six divisions per age/gender group, six teams per division: 396 games every Sunday (US$ 40 per referee; U$ 20 per linesman, two linesmen) • Problem: assign referees to games Duarte, Ribeiro & Urrutia (PATAT 2006, LNCS 2007) • Referee assignment involves many constraints La Havana, March 2009 Metaheuristics for optimization problems in sports 57 and multiple objectives

Referee assignment • Possible constraints: – Different number of referees may be necessary for each game – Games require referees with different levels of certification: higher division games require referees with higher skills – A referee cannot be assigned to a game where he/she is a player – Timetabling conflicts and traveling times La Havana, March 2009 58 Metaheuristics for optimization problems in sports

Referee assignment • Possible constraints (cont. ): – Referee groups: cliques of referees that request to be assigned to the same games (relatives, car pools, no driver’s licence) • Hard links • Soft links – Number of games a referee is willing to referee – Traveling constraints – Referees that can officiate games only at a certain location or period of the day La Havana, March 2009 59 Metaheuristics for optimization problems in sports

Referee assignment • Possible objectives: – Difference between the target number of games a referee is willing to referee and the number of games he/she is assigned to – Traveling/idle time between consecutive games – Number of inter-facility travels – Number of games assigned outside his/her preferred time-slots or facilities – Number of violated soft links La Havana, March 2009 60 Metaheuristics for optimization problems in sports

Problem statement • Games are already scheduled (facility – time slot) • Each game has a number of refereeing positions to be assigned to referees • Each refereeing position to be filled by a referee is called a refereeing slot • S = {s 1, s 2, . . . , sn}: refereeing slots to be filled by referees • R = {r 1, r 2, . . . , rm}: referees La Havana, March 2009 61 Metaheuristics for optimization problems in sports

Problem statement • pi: skill level of referee ri • qj: minimum skill level a referee must have to be assigned to refereeing slot sj • Mi: maximum number of games referee ri can officiate • Ti: target number of games referee ri is willing to officiate • Each referee may choose a set of time slots where he/she is not available to officiate La Havana, March 2009 62 Metaheuristics for optimization problems in sports

Problem statement • Problem: assign a referee to each refereeing slot • Constraints: – Referees officiate in a single facility on the same day – Minimum skill level requirements – Maximum number of games – Timetabling conflicts and availability • Objective: minimize the sum over all referees of the absolute value of the difference between the March target number of games La Havana, 2009 and the actual Metaheuristics for optimization problems in sports 63

Solution approach • Three-phase heuristic approach 1. Greedy constructive heuristic 2. ILS-based repair heuristic to make the initial solution feasible (if necessary): minimization of the number of violations 3. ILS-based procedure to improve a feasible solution La Havana, March 2009 64 Metaheuristics for optimization problems in sports

Solution approach Algorithm Referee. Assignment. Heuristic (Max. Iter) 1. S* Build. Greedy. Randomized. Solution (); 2. If not is. Feasible (S*) then 3. S* Repair. Heuristic (S*, Max. Iter); 4. If is. Feasible (S*) then 5. S* Improvement. Heuristic (S*); 6. Else “infeasible” 7. Return S* La Havana, March 2009 65 Metaheuristics for optimization problems in sports

Numerical results • Randomly generated instances following patterns similar to real-life applications • Instances with up to 500 games and 1, 000 referees – Different number of facilities – Different patterns of the target number of games • Five different instances for each configuration • Max. Iter = 1, 000 66 Metaheuristics for optimization problems in sports La Havana, March 2009

Numerical results • For each instance, average time and average objective value over ten runs • Codes implemented in C • Results on a 2. 0 GHz Pentium IV processor with 256 Mbytes • Initial solutions: – greedy constructive heuristic – random assignments (to test the repair heuristic) La Havana, March 2009 67 Metaheuristics for optimization problems in sports

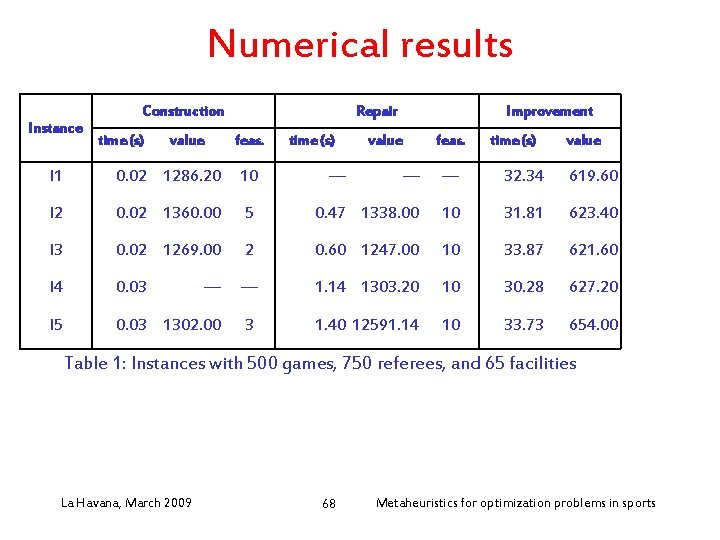
Numerical results Instance Construction time (s) value Repair feas. I 1 0. 02 1286. 20 10 I 2 0. 02 1360. 00 I 3 time (s) — Improvement value feas. time (s) value — — 32. 34 619. 60 5 0. 47 1338. 00 10 31. 81 623. 40 0. 02 1269. 00 2 0. 60 1247. 00 10 33. 87 621. 60 I 4 0. 03 — — 1. 14 1303. 20 10 30. 28 627. 20 I 5 0. 03 1302. 00 3 1. 40 12591. 14 10 33. 73 654. 00 Table 1: Instances with 500 games, 750 referees, and 65 facilities La Havana, March 2009 68 Metaheuristics for optimization problems in sports

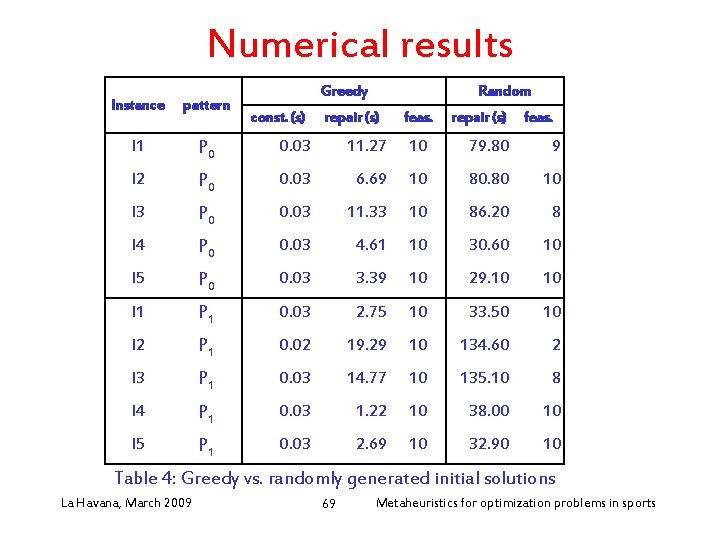
Numerical results Greedy Random Instance pattern I 1 P 0 0. 03 11. 27 10 79. 80 9 I 2 P 0 0. 03 6. 69 10 80. 80 10 I 3 P 0 0. 03 11. 33 10 86. 20 8 I 4 P 0 0. 03 4. 61 10 30. 60 10 I 5 P 0 0. 03 3. 39 10 29. 10 10 I 1 P 1 0. 03 2. 75 10 33. 50 10 I 2 P 1 0. 02 19. 29 10 134. 60 2 I 3 P 1 0. 03 14. 77 10 135. 10 8 I 4 P 1 0. 03 1. 22 10 38. 00 10 I 5 P 1 0. 03 2. 69 10 32. 90 10 const. (s) repair (s) feas. Table 4: Greedy vs. randomly generated initial solutions La Havana, March 2009 69 Metaheuristics for optimization problems in sports

Improvements and extensions • Greedy constructive heuristic: – First, assign each referee to a number of refereeing slots as close as possible to his/her target number of games – Second, if there are still unassigned slots, assign more games to each referee • Improvement heuristic: – After each perturbation, instead of applying a local search to both facilities involved in this perturbation, solve a MIP model associated with the subproblem considering all refereeing slots and referees corresponding to these facilities La Havana, March 2009 Metaheuristics for optimization problems in sports (“MIP it!”) 70

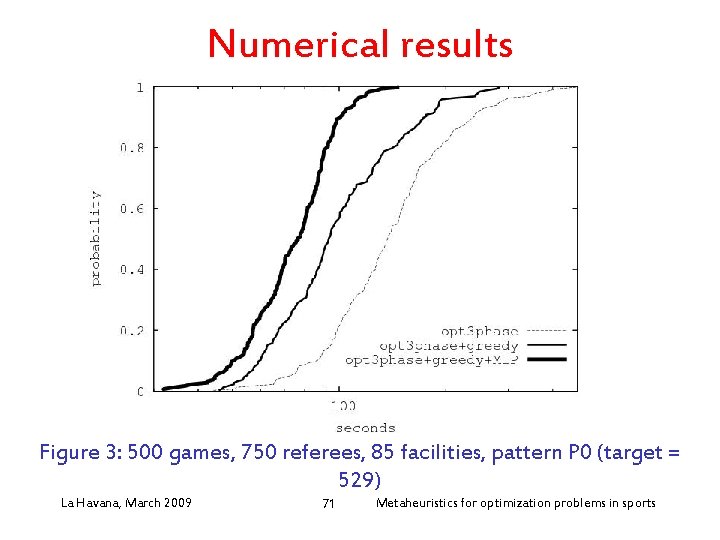
Numerical results Figure 3: 500 games, 750 referees, 85 facilities, pattern P 0 (target = 529) La Havana, March 2009 71 Metaheuristics for optimization problems in sports

Bi-criteria problem (bi. RAP) • • Same constraints as in the single objective version Objectives: 1. minimize the sum over all referees of the absolute value of the difference between the target and the actual number of games assigned to each referee 2. minimize the sum over all referees of the total idle time between consecutive games La Havana, March 2009 72 Metaheuristics for optimization problems in sports

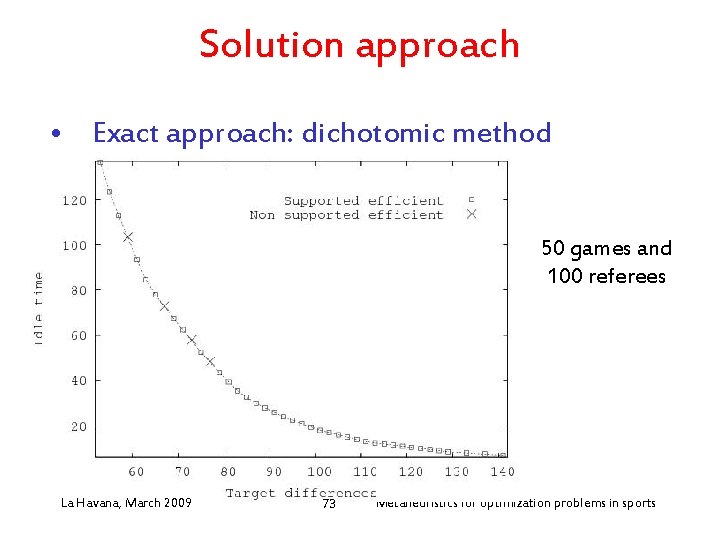
Solution approach • Exact approach: dichotomic method 50 games and 100 referees La Havana, March 2009 73 Metaheuristics for optimization problems in sports

Solution approach • Heuristic approach: – Perform three-phase ILS-based heuristic for a fixed number of search directions – Each search direction represents a set of weights associated with each objective – Directions are chosen as in the dichotomic method – All new potentially efficient solutions found during the search are progressively stored – Former potentially efficient solutions are discarded during the search (quadtree is used) – Perform a post-optimization path-relinking La Havana, procedure March 2009 Metaheuristics for optimization problems in sports 74

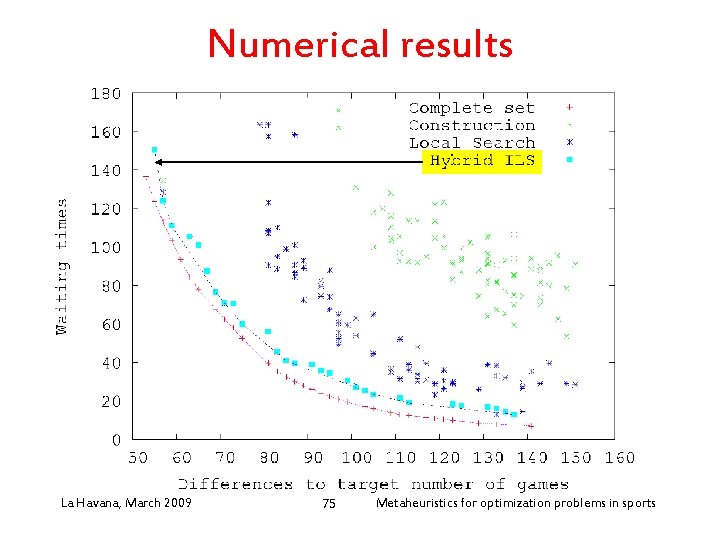
Numerical results La Havana, March 2009 75 Metaheuristics for optimization problems in sports

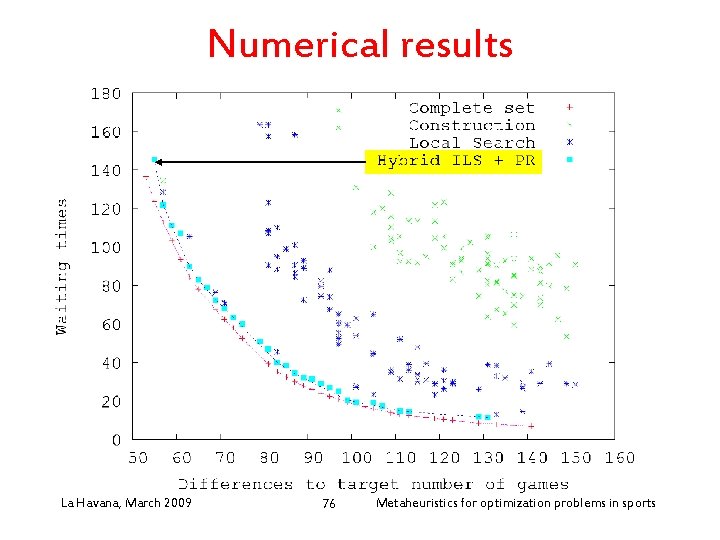
Numerical results La Havana, March 2009 76 Metaheuristics for optimization problems in sports

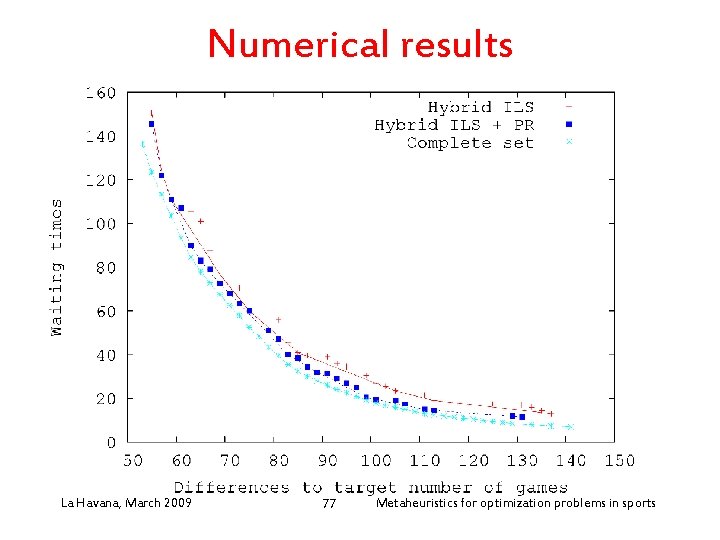
Numerical results La Havana, March 2009 77 Metaheuristics for optimization problems in sports

Conclusions • New optimization problem in sports • Effective heuristics: construction, repair, improvement, path relinking • Quick procedures to build good initial solutions • Bicriteria approach finds good approximations of the Pareto frontier • Other constraints and criteria may be considered La Havana, March 2009 78 Metaheuristics for optimization problems in sports

Applications of metaheuristics Carry-over minimization problem La Havana, March 2009 79 Metaheuristics for optimization problems in sports

Carry-over effects • Team B receives a carry-over effect (COE) due to team A if there is a team X that plays A in round r and B in round r+1 La Havana, March 2009 80 Metaheuristics for optimization problems in sports

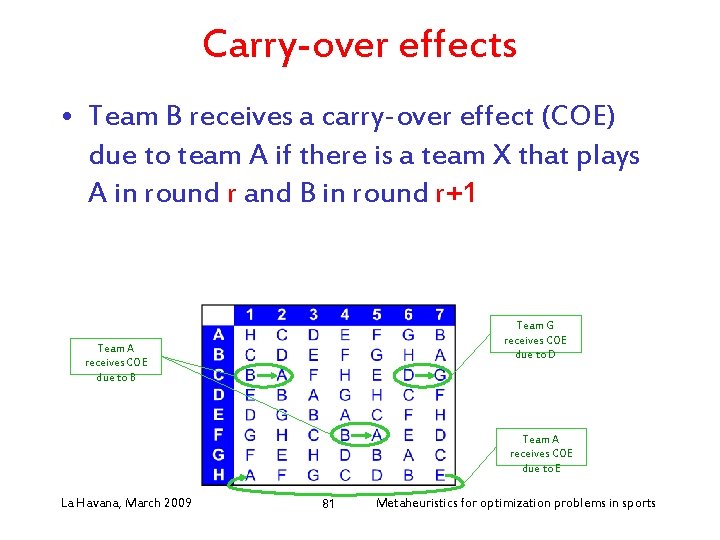
Carry-over effects • Team B receives a carry-over effect (COE) due to team A if there is a team X that plays A in round r and B in round r+1 Team G receives COE due to D Team A receives COE due to B Team A receives COE due to E La Havana, March 2009 81 Metaheuristics for optimization problems in sports

Carry-over effects matrix • SRRT and carry-over effects matrix (COEM) COE matrix RRT La Havana, March 2009 82 Metaheuristics for optimization problems in sports

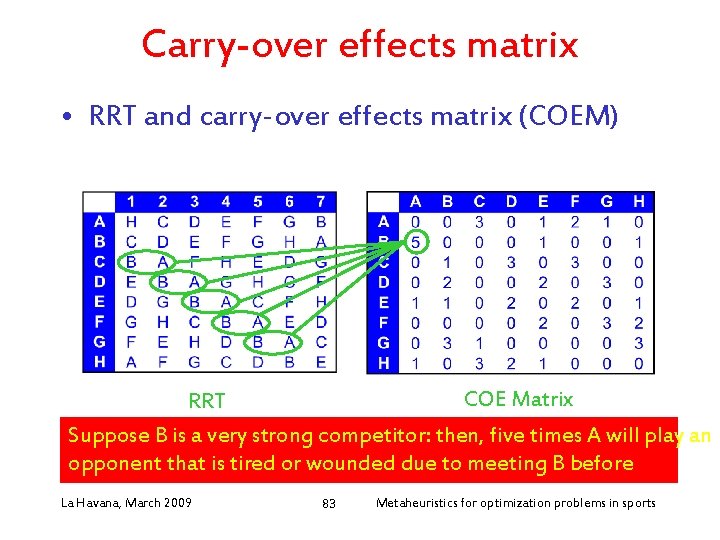
Carry-over effects matrix • RRT and carry-over effects matrix (COEM) COE Matrix RRT Suppose B is a very strong competitor: then, five times A will play an opponent that is tired or wounded due to meeting B before La Havana, March 2009 83 Metaheuristics for optimization problems in sports

Carry-over effects value COEMDG = 3 COEMFH = 2 COE matrix La Havana, March 2009 84 Metaheuristics for optimization problems in sports

Carry-over effects value COEMDG = 3 COEMFH = 2 COE Matrix Minimize!!! La Havana, March 2009 85 Metaheuristics for optimization problems in sports

Example • Karate-Do competitions • Groups playing round-robin tournaments – Pan-american Karate-Do championship – Brazilian classification for World Karate-Do championship • Open weight categories – Physically strong contestants may fight weak ones – One should avoid that a competitor benefits from fighting (physically) tired opponents La Havana, March 2009 Metaheuristics for optimization problems in sports 86 coming from matches against strong athletes

Problem statement • Find a schedule with minimum COEV – RRT distributing the carry-over effects as evenly as possible among the teams • Best solution approaches to date in literature: – Random generation of 1 -factors permutations – Constraint Programming – Combinatorial designs La Havana, March 2009 87 Metaheuristics for optimization problems in sports

Solution approach • Multi-start + ILS heuristic • Solutions represented by 1 -factorizations – Canonical factorizations – Binary 1 -factorizations • Constructive algorithms – Rearrangement of the 1 -factors of a solution (TSP-like greedy algorithms) • Nearest neighbor • Arbitrary insertion La Havana, March 2009 88 Metaheuristics for optimization problems in sports

Solution approach • Local search – Rearrangement of the 1 -factors of the solution (TSP-like procedures) – Partial Round Swap (PRS) • Pertubations – Ejection chain: Game Rotation (GR) neighborhood La Havana, March 2009 89 Metaheuristics for optimization problems in sports

Perspectives and concluding remarks • Wiki. Sport: Application to Brazilian nationalmaintained basketball by the open content project tournament Working Group on Operations Research Applied to (UFF andin. UFMG, at of increasing interest • Sports Optimization sports. Brazil) is a field • http: //www. esportemax. com Very attractive area for Operations Research Kendall, Knust, Ribeiro & Urrutia (2008): “Scheduling in applications annotated bibliography” (200 references) • sports: Many. An interesting applications, often reviewed by the media Confederation last • Brazilian Student. Soccer motivation: OR course(CBF) withannounced sports problems month the fixture of its 2009 First Division, which was • Several problems with interesting theoretical structure the first built by an automatic optimization system • Next Evenyear: small allinstances divisions are hard to solve (e. g. , TTP for n=10) Havana, March 2009 Metaheuristics for optimization problems in sports 90 • La. Quick construction procedures to build good initial

La Havana, March 2009 91 Metaheuristics for optimization problems in sports