Applications of Linear and Integer Programming Models 1

Applications of Linear and Integer Programming Models 1

Applications of Integer Linear Programming Models Many real life problems call for at least one integer decision variable. n There are three types of Integer models: n Pure integer (AILP) n Mixed integer (MILP) n Binary (BILP) n 2

The use of binary variables in constraints • AAny decision situation that can be modeled by “yes”/“no”, “good”/“bad” etc. , falls into the binary category. n To illustrate 3

The use of binary variables in constraints n Example n A decision is to be made whether each of three plants should be built (Yi = 1) or not built (Yi = 0) Requirement Binary Representation At least 2 plants must be built Y 1 + Y 2 + Y 3 ³ 2 If plant 1 is built, plant 2 must not be built Y 1 + Y 2 £ 1 If plant 1 is built, plant 2 must be built Y 1 – Y 2 £ 0 One, but not both plants must be built Y 1+ Y 2 = 1 Both or neither plants must be built Y 1 – 4

The use of binary variables in constraints n Example - continued n Two products can be produced at a plant. • Product 1 requires 6 pounds of steel and product 2 requires 9 pounds. • If a plant is built, it should have 2000 pounds of steel available. n The production of each product should satisfy the steel availability if the plant is opened, or equal to zero if the plant is not opened. If the plant is not built Y 1 = 0 6 X + 9 X £ 2000 Y 1 The constraint becomes If the plant is 1 built Y 1 =21. The constraint becomes 6 x 1 + 9 X 2 £ 2000 6 x 1 + 9 X 2 £ 0, and thus, X 1 = 0 and X 2 = 0 5

Personnel Scheduling Models Assignments of personnel to jobs under minimum required coverage is a typical integer problems. n When resources are available over more than one period, linking constraint link the resources available in period t to the resources available in a period t+1. n 6

7

y n un Y Yoouu l l o o You look o so funny o kks so o funn y fu n n y Yo u l so f oo so funny k You olook o k l so u fun Yo ny y n n n You look so funny u f fu o s okkso o l You loo u o Y 8

Sunset Beach Lifeguard Assignments n The City of Sunset Beach staffs lifeguards 7 days a week. n Regulations require that city employees work five days. n Insurance requirements mandate 1 lifeguard per 8000 average daily attendance on any given day. n The city wants to employ as few 9

Sunset Beach Lifeguard Assignments n Problem Summary Schedule lifeguard over 5 consecutive days. n Minimize the total number of lifeguards. n Meet the minimum daily lifeguard requirements Sun. Mon. Tue. Wed. Thr. Fri. Sat. 8 6 5 4 6 7 9 n 10

Sunset Beach Lifeguard Assignments n Decision Variables Xi = the number of lifeguards scheduled to begin on day “ i ” for i=1, 2, …, 7 (i=1 is Sunday) n n Objective Function Minimize the total number of lifeguard scheduled Constraints Ensure that enough lifeguards are scheduled each day. 11

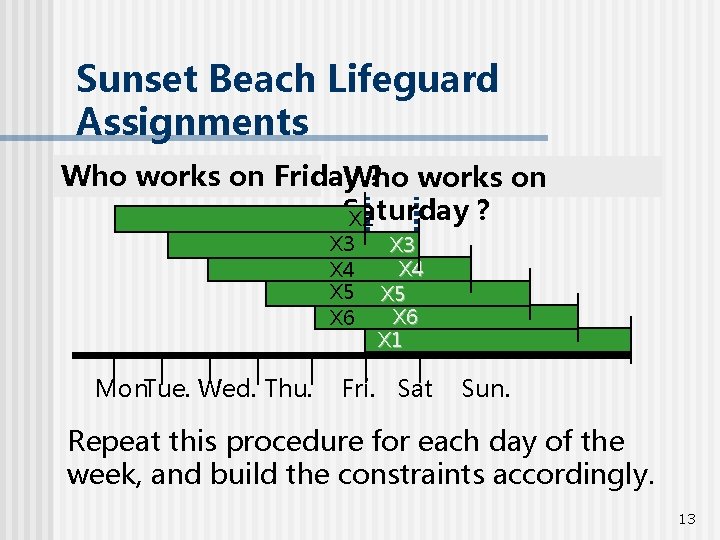
Sunset Beach Lifeguard Assignments To ensure that enough lifeguards are schedu each day, identify which workers are on duty For example: … 12

Sunset Beach Lifeguard Assignments Who works on Friday ? works on Who Saturday ? X 2 X 3 X 4 X 5 X 6 Mon. Tue. Wed. Thu. X 3 X 4 X 5 X 6 X 1 Fri. Sat Sun. Repeat this procedure for each day of the week, and build the constraints accordingly. 13

Sunset Beach Lifeguard Assignments Min. X 1 + S. T. X 1 + 8 X 1 + 6 X 1 + 5 X 1 + 4 X 1 + X 2 + X 3 + X 4 + X 5 + X 6 + X 7 ³ X 2 + X 5 + X 6 + X 7 ³ X 2 + X 3 + X 4 + X 5 ³ 14

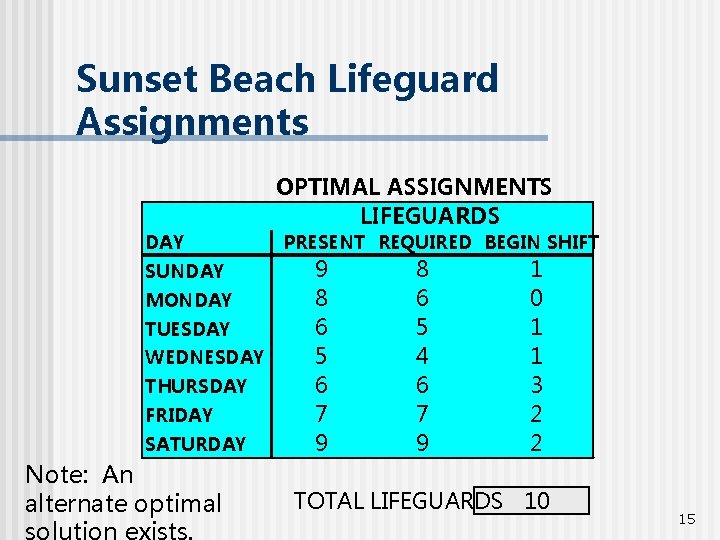
Sunset Beach Lifeguard Assignments OPTIMAL ASSIGNMENTS LIFEGUARDS DAY SUNDAY MONDAY TUESDAY WEDNESDAY THURSDAY FRIDAY SATURDAY Note: An alternate optimal PRESENT REQUIRED BEGIN SHIFT 9 8 6 5 6 7 9 8 6 5 4 6 7 9 1 0 1 1 3 2 2 TOTAL LIFEGUARDS 10 15

Project selection Models These models involve a “go/no-go” situations, that can be modeled using binary variables. n Typical elements in such models are: n Budget n Space n Priority conditions n 16

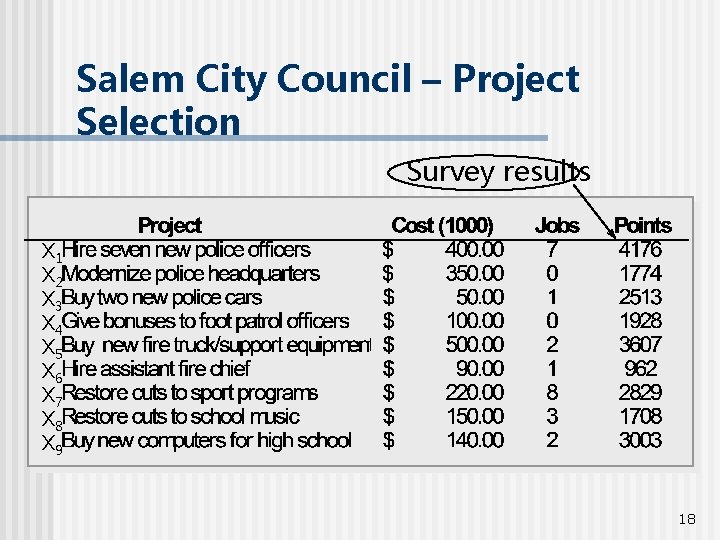
Salem City Council – Project Selection The Salem City Council needs to decide how to allocate funds to nine projects such that public support is maximized. n Data reflect costs, resource availabilities, concerns and priorities the city council has. n 17

Salem City Council – Project Selection Survey results X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 18

Salem City Council – Project Selection n Decision Variables: Xj- a set of binary variables indicating if a project j is selected (Xj=1) or not (Xj=0) for j=1, 2, . . , 9. n Objective function: Maximize the overall point score of the funded projects n Constraints: See the mathematical model. 19

Salem City Council – Project Selection n (Xi = 0, 1 for i=1, 2…, 9) The Mathematical Model Max 4176 X 1+1774 X 2+ maximum amounts funds 7+1708 X to be allocated 2513 XThe +2829 X 3+1928 X 4+3607 X 5+962 X 6 of 8+3003 X 9 is $900, 000 S. T. 400 X 1 of + new 350 Xjobs 50 X 3+ 100 X 90 X 6+ 2+ 5+ The number created must 4+be 500 X at least 10 220 X 7+ 150 X 8+ 140 X 9 £ 900 The number of police-related activities selected is at most 3 7 X 1+ X 3+ 2 X 5+ (out of 4) X 6+ 8 X + 3 X 8+ 2 x 9 ³ 10 Either 7 police car or fire truck be purchased X 1+ X 5 X 2+ X 3+ X 4 Sports funds and music funds must be restored / not £ 3 restored together Sports funds and music funds must be X 3+ restored before computer equipment is purchased = 1 20