Applications of Integration Volumes Arc Lengths Surface Areas

Applications of Integration Volumes Arc Lengths Surface Areas of Polar Domains

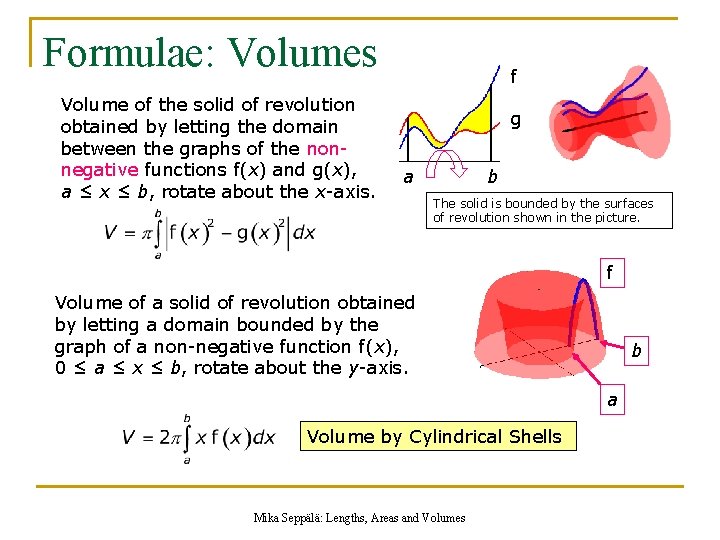
Summary of Formulae Area bounded by the Graph of a Function Area between the Graphs of Functions Volume of a Solid of Revolution Volume of the solid of revolution by letting the domain between the graphs of the non-negative functions f and g rotate about the x-axis. Volume by Cylindrical Shells Mika Seppälä: Lengths, Areas and Volumes

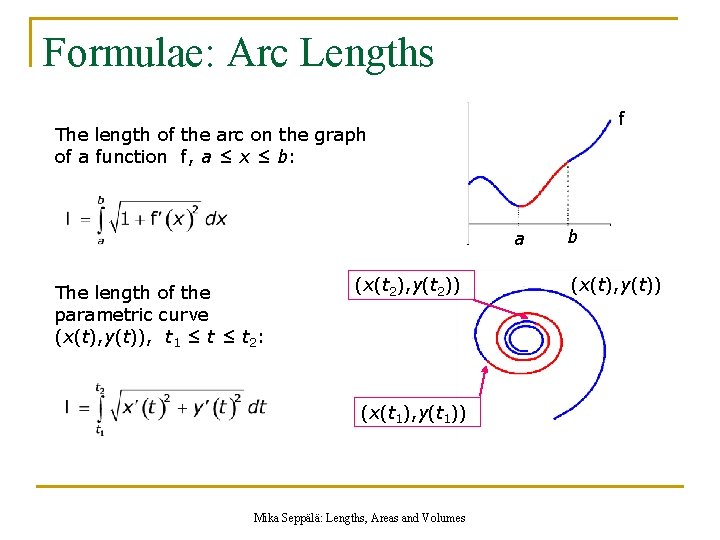
Summary of Formulae Volumes by Slicing At= the area of a slice Arc Length of a Parametric Curve The Area of a Surface of Revolution The Area of a Polar Domain Mika Seppälä: Lengths, Areas and Volumes

Overview of Problems 1/3 1 The bottom of a bowler is a disk of radius r with center at the origin. Every intersection of the bowler with a plane perpendicular to x axis is a semicircle. Compute the volume of the bowler. 2 Find the volume of the solid of revolution obtained by letting the domain bounded by the graph of the function f(x) = x - x 2 and the x-axis rotate around the x-axis. 3 Find the volume of the solid of revolution obtained by letting the domain in Problem 2 rotate around the y –axis. 4 Find the volume of the solid of revolution obtained by letting the disk bounded by the circle (x-2)2 + y 2 =1 rotate around the y –axis. 5 Compute the volume of the cap of a ball x 2+y 2+z 2 r 2 which lies above the plane z=r-h. 6 Determine the volume of the intersection of the cylinders x 2+z 2 1 and y 2+z 2 1. Mika Seppälä: Lengths, Areas and Volumes

Overview of Problems 2/3 7 Determine the length of the arc on the graph of the function cosh(x) over the interval [-1, 1]. 8 9 10 11 Find the area of the surface obtained by rotating the curve y = x 3, 0 ≤ x ≤ 1, about the x-axis. 12 13 Mika Seppälä: Lengths, Areas and Volumes

Overview of Problems 3/3 14 15 Use Maple to plot the polar curve r = 1 + cos(2θ), 0 ≤ θ ≤ 2π. Find the area of the domain bounded by this curve. Mika Seppälä: Lengths, Areas and Volumes

Computing Volumes Problem 1 Solution The bottom of a bowler is a disk of radius r with center at the origin. Every intersection of the bowler with a plane perpendicular to x axis is a semicircle. Compute the volume of the bowler. This bowler is a half of a ball of radius r. Hence the volume is half of the volume of a ball of radius r. To compute the volume of the bowler by integration, slice it with planes perpendicular to the x-axis as indicated in the picture. The slice is a semicircle of radius (r 2 -x 2) 1/2. The area of the slice is A(x)= (r 2 -x 2)/2. Conclude Mika Seppälä: Lengths, Areas and Volumes x

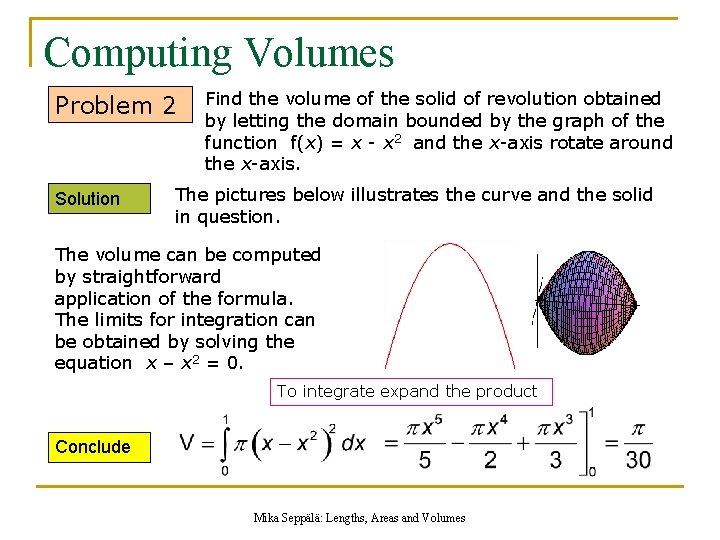
Computing Volumes Problem 2 Solution Find the volume of the solid of revolution obtained by letting the domain bounded by the graph of the function f(x) = x - x 2 and the x-axis rotate around the x-axis. The pictures below illustrates the curve and the solid in question. The volume can be computed by straightforward application of the formula. The limits for integration can be obtained by solving the equation x – x 2 = 0. To integrate expand the product Conclude Mika Seppälä: Lengths, Areas and Volumes

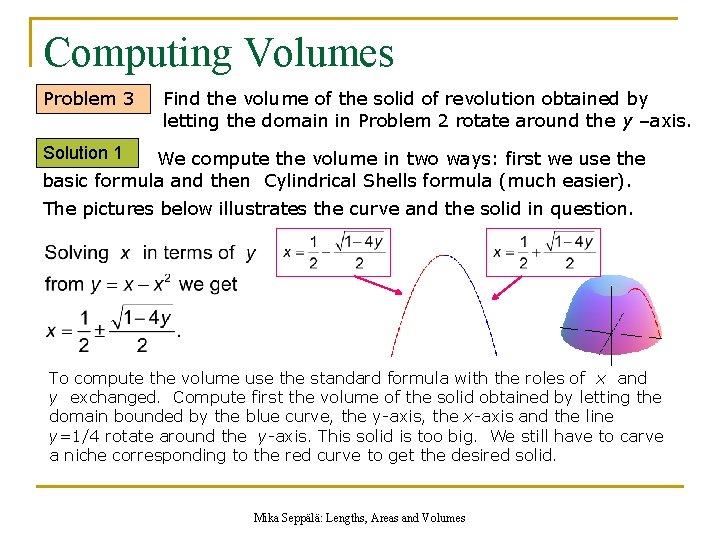
Computing Volumes Problem 3 Find the volume of the solid of revolution obtained by letting the domain in Problem 2 rotate around the y –axis. Solution 1 We compute the volume in two ways: first we use the basic formula and then Cylindrical Shells formula (much easier). The pictures below illustrates the curve and the solid in question. To compute the volume use the standard formula with the roles of x and y exchanged. Compute first the volume of the solid obtained by letting the domain bounded by the blue curve, the y-axis, the x-axis and the line y=1/4 rotate around the y-axis. This solid is too big. We still have to carve a niche corresponding to the red curve to get the desired solid. Mika Seppälä: Lengths, Areas and Volumes

Computing Volumes Problem 3 Find the volume of the solid of revolution obtained by letting the domain in Problem 2 rotate around the y –axis. Solution 1 (cont’d) We compute the volume in two steps. First we compute the volume V 1 of the solid obtained by letting the domain bounded by the blue curve and the coordinate axes rotate around the y-axis. From that we subtract the volume V 2 corresponding to the red curve in the picture i. e. we carve a niche in the first solid which was too big. Mika Seppälä: Lengths, Areas and Volumes

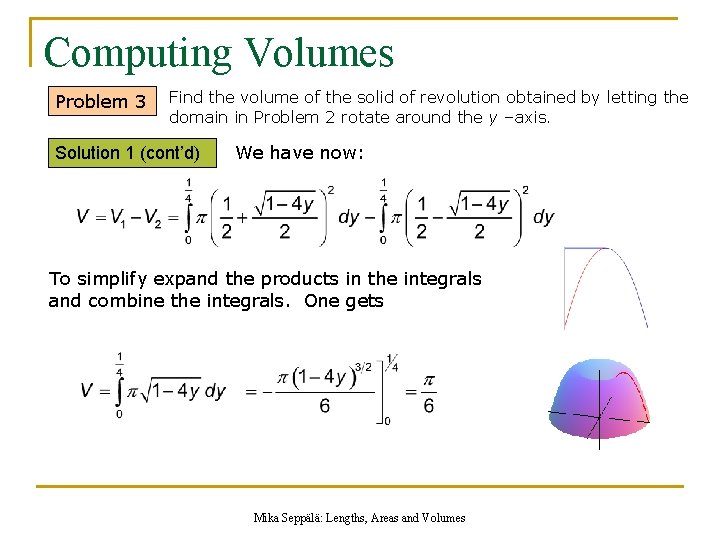
Computing Volumes Problem 3 Find the volume of the solid of revolution obtained by letting the domain in Problem 2 rotate around the y –axis. Solution 1 (cont’d) We have now: To simplify expand the products in the integrals and combine the integrals. One gets Mika Seppälä: Lengths, Areas and Volumes

Computing Volumes Problem 3 Find the volume of the solid of revolution obtained by letting the domain in Problem 2 rotate around the y – axis. Solution 2 by Cylindrical Shells Using the Cylindrical Shells Formula the computation is much easier: Mika Seppälä: Lengths, Areas and Volumes

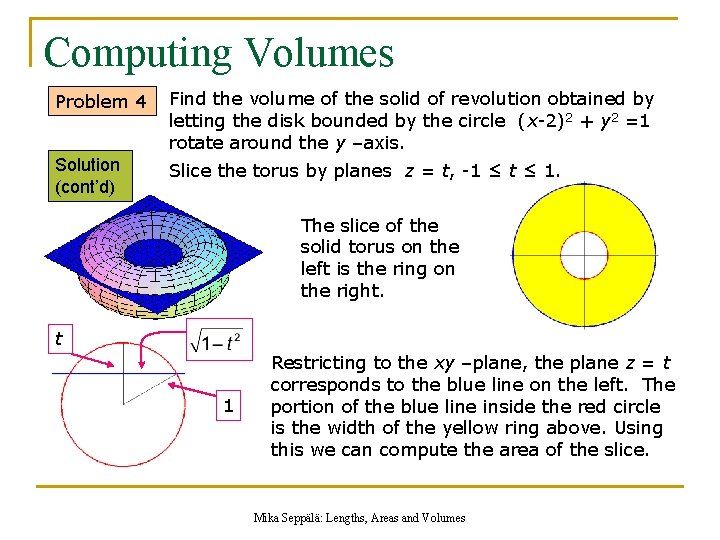
Computing Volumes Problem 4 Solution Find the volume of the solid of revolution obtained by letting the disk bounded by the circle (x-2)2 + y 2 =1 rotate around the y –axis. The first task is to form a correct geometric picture of the solid. The disk pictured on the left rotates around the vertical axis and forms the torus on the right The volume can be computed in two ways. One can adapt the method presented in the lecture on Volumes or one can slice the solid in an appropriate way. Here we will use the slicing method. Mika Seppälä: Lengths, Areas and Volumes

Computing Volumes Problem 4 Find the volume of the solid of revolution obtained by letting the disk bounded by the circle (x-2)2 + y 2 =1 rotate around the y –axis. Solution (cont’d) Slice the torus by planes z = t, -1 ≤ t ≤ 1. The slice of the solid torus on the left is the ring on the right. t 1 Restricting to the xy –plane, the plane z = t corresponds to the blue line on the left. The portion of the blue line inside the red circle is the width of the yellow ring above. Using this we can compute the area of the slice. Mika Seppälä: Lengths, Areas and Volumes

Computing Volumes Problem 4 Solution (cont’d) Find the volume of the solid of revolution obtained by letting the disk bounded by the circle (x-2)2 + y 2 =1 rotate around the y – axis. Slice the torus by planes z = t, -1 ≤ t ≤ 1. t 1 2 The blue line is the intersection of the plane z = t in the xy –plane. Mika Seppälä: Lengths, Areas and Volumes

Computing Volumes Problem 4 Solution (cont’d) Find the volume of the solid of revolution obtained by letting the disk bounded by the circle (x-2)2 + y 2 =1 rotate around the y – axis. To get the volume V of the solid, simply integrate the area of a general slice. 2 The above integral can also be computed by a substitution, see the lecture on Volumes. Mika Seppälä: Lengths, Areas and Volumes

Computing Volumes Problem 5 Compute the volume of the cap of a ball x 2+y 2+z 2 r 2 Solution which lies above the plane z=r-h. The solid in question is the cap of the ball above the red plane z=r-h. We slice the solid by planes parallel to the red plane in the picture. A slice by the plane z = t is a disk of radius (r 2 -t 2)1/2. area of a slice is (r 2 -t 2). Conclude Mika Seppälä: Lengths, Areas and Volumes Hence the

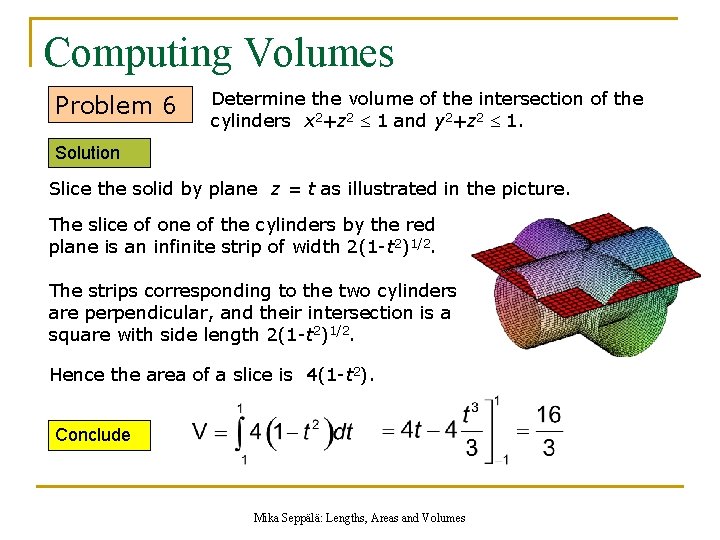
Computing Volumes Problem 6 Determine the volume of the intersection of the cylinders x 2+z 2 1 and y 2+z 2 1. The picture on the right illustrates the solid in question. The key to being able to compute the volume is to slice the cylinders and the solid in question properly. Mika Seppälä: Lengths, Areas and Volumes

Computing Volumes Problem 6 Determine the volume of the intersection of the cylinders x 2+z 2 1 and y 2+z 2 1. Solution Slice the solid by plane z = t as illustrated in the picture. The slice of one of the cylinders by the red plane is an infinite strip of width 2(1 -t 2)1/2. The strips corresponding to the two cylinders are perpendicular, and their intersection is a square with side length 2(1 -t 2)1/2. Hence the area of a slice is 4(1 -t 2). Conclude Mika Seppälä: Lengths, Areas and Volumes

Computing Arc Lengths Problem 7 Solution Determine the length of the arc on the graph of the function cosh(x) over the interval [-1, 1]. This is a straightforward application of the Arc Length Formula. . Mika Seppälä: Lengths, Areas and Volumes

Computing Arc Lengths Problem 8 Solution This is a straightforward application of the formula. Intermediate simplifications are rather technical, and one should use Maple there. We get: Use Maple to integrate. Mika Seppälä: Lengths, Areas and Volumes

Computing Arc Lengths Problem 9 Solution By the Fundamental Theorem of Calculus, Mika Seppälä: Lengths, Areas and Volumes

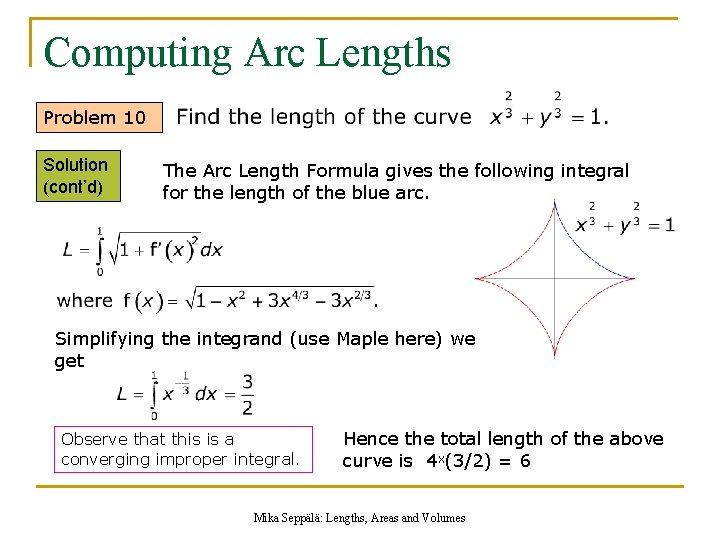
Computing Arc Lengths Problem 10 Solution One observes first that the curve is perfectly symmetric with respect to both x- and the yaxis. Using this observation the curve can be plotted by Maple. The expression for f was obtained by solving y in terms of x form the equation of the curve. Next use the Arc Length Formula to compute the length of the blue arc. The length of the curve is then simply four times the length of the blue arc. Mika Seppälä: Lengths, Areas and Volumes

Computing Arc Lengths Problem 10 Solution (cont’d) The Arc Length Formula gives the following integral for the length of the blue arc. Simplifying the integrand (use Maple here) we get Observe that this is a converging improper integral. Hence the total length of the above curve is 4 x(3/2) = 6 Mika Seppälä: Lengths, Areas and Volumes

Surface Areas Problem 11 Solution Find the area of the surface obtained by rotating the curve y = x 3, 0 ≤ x ≤ 1, about the x-axis. This is a straightforward computation using the formula for the area. We get Use the substitution t = 1 + 9 x 4. Mika Seppälä: Lengths, Areas and Volumes

Surface Areas Problem 12 Solution This is a straightforward computation using the formula for the area. We get Combine the square roots. Use the substitution 2 x 2=sinh 2(t). Mika Seppälä: Lengths, Areas and Volumes

Polar Domains Problem 13 Solution This is a straightforward computation using the formula for the area. We get Mika Seppälä: Lengths, Areas and Volumes

Polar Domains Problem 14 Solution It is useful to plot the curves in question first. Intersection points: This integral is the area bounded by the red curve in the sector π/3≤θ≤ π/3 minus the area bounded by the blue curve in the same sector. Mika Seppälä: Lengths, Areas and Volumes

Polar Domains Problem 15 Solution Use Maple to plot the polar curve r = 1 + cos(2θ), 0 ≤ θ ≤ 2π. Find the area of the domain bounded by this curve. The Maple command plot([1+cos(2*t), t, t=0. . 2*Pi], coords=polar); gives the plot below The polar curve r = 1 + cos(2θ) Mika Seppälä: Lengths, Areas and Volumes

Formulae: Areas and Volumes Area between a curve and the x-axis b a Area between the graphs of the functions f(x) and g(x), a≤x≤b: f f g a b Volume of a solid of revolution obtained by letting the domain between the graph of a function f, a≤x≤b, and the x-axis rotate about the x-axis. Mika Seppälä: Lengths, Areas and Volumes

Formulae: Volumes Volume of the solid of revolution obtained by letting the domain between the graphs of the nonnegative functions f(x) and g(x), a ≤ x ≤ b, rotate about the x-axis. f g a b The solid is bounded by the surfaces of revolution shown in the picture. f Volume of a solid of revolution obtained by letting a domain bounded by the graph of a non-negative function f(x), 0 ≤ a ≤ x ≤ b, rotate about the y-axis. b a Volume by Cylindrical Shells Mika Seppälä: Lengths, Areas and Volumes

Formulae: Arc Lengths f The length of the arc on the graph of a function f, a ≤ x ≤ b: a The length of the parametric curve (x(t), y(t)), t 1 ≤ t 2: (x(t 2), y(t 2)) (x(t 1), y(t 1)) Mika Seppälä: Lengths, Areas and Volumes b (x(t), y(t))

Formulae: the Area of a Surface of Revolution f The area of the surface of revolution obtained by letting the graph of the function f(x), a ≤ x ≤ b, rotate about the x-axis. a Mika Seppälä: Lengths, Areas and Volumes b

Formulae: Area of Polar Domains The area of a domain bounded by the polar curve r = r(θ), and the half lines θ=θ 1, θ=θ 2: θ=θ 2 Mika Seppälä: Lengths, Areas and Volumes θ=θ 1