Applications of Hahn Banach Theorem E normed vector

Applications of Hahn Banach Theorem

E: normed vector space, assumed to be real for definitions Known: Taking We have
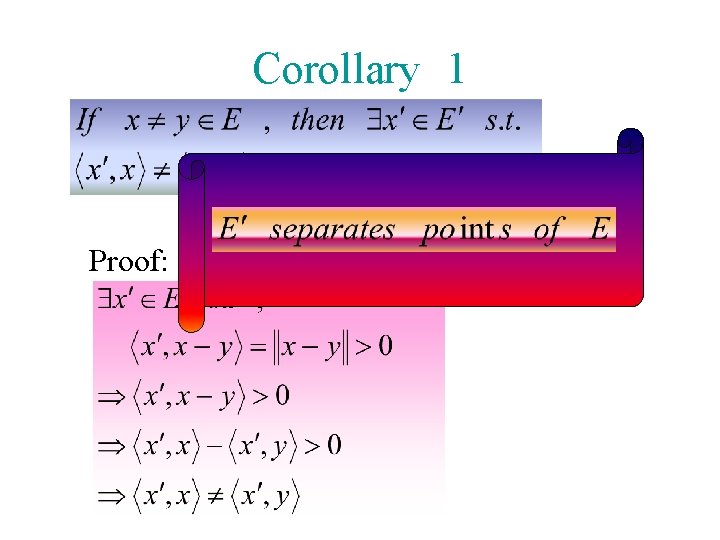
Corollary 1 Proof:

Corollary 2 Proof in next page This corollary implies that We may consider E as embedded in as normed space, then complete space which is the completion of E. is a


A dual variational principle



Example Why? See next page
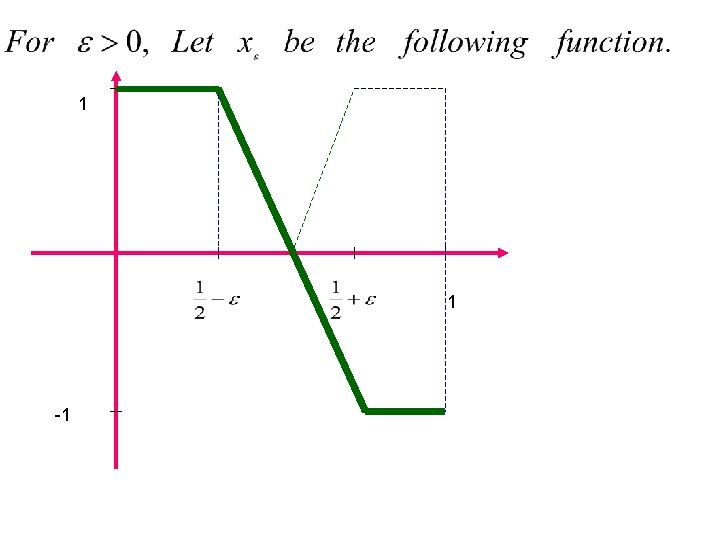
1 1 -1


Claim In this example

Exercise

Suppose that such that , then


Applications of Mazm. Orlich Theorem

is the space of the probability measure of S
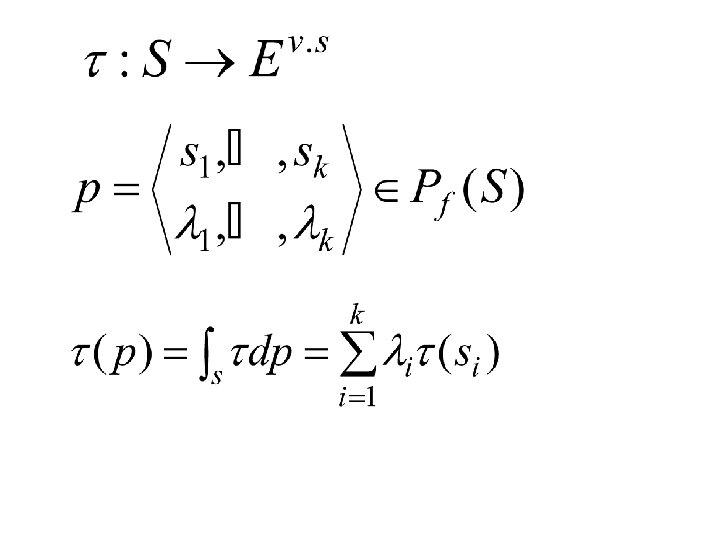

Mazm-Orlich Theorem

Mazur-Orlicz (1953) S : arbitary set E : real vector space sublinear (I)


Corollary 1 Let then be as in Mazur-Orlicz Theorem



Corollary 2 If in Corollary 1 sastisfies the condition: For each there is then such that


Example p. 1 S: arbitary set defined by Then


Example p. 2 is q-convex

Example p. 3 In particular, S is a convex set in a linear map is convex i. e. Then This implies von Neumann Minimax Theorem


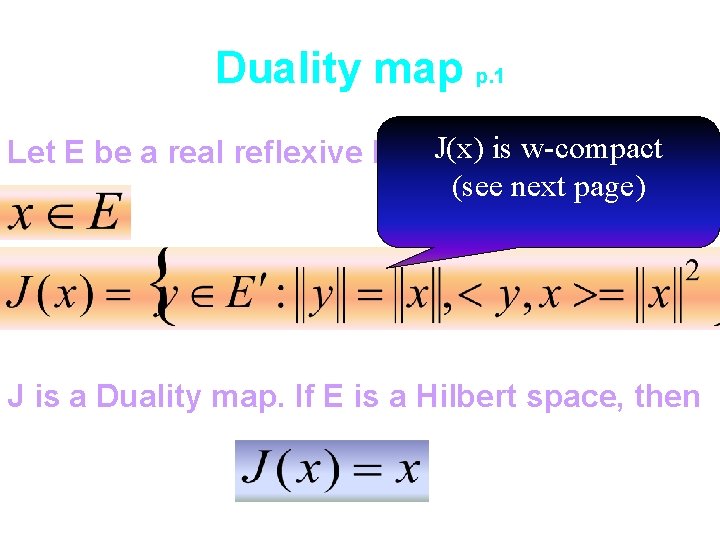
Duality map p. 1 J(x) is w-compact Let E be a real reflexive Banach space. For (see next page) J is a Duality map. If E is a Hilbert space, then


Lemma p. 1 Let S be a compact convex subset of a linear function topological linear space. Define+constant If and F is the space of all affine functions then



Theorem p. 1 Let E be a real reflexive Banach space is bilinear such that (i) There is c>0 such that (ii )

Theorem p. 2 Then for each with there is a unique such that





Variational Inequality (Stampachia-Hartmam) p. 1 E: reflexive Banach space C: closed bounded convex set in E satisfies (i) f is monotone i. e. (ii) f is weakly continuous on each line segment in C.
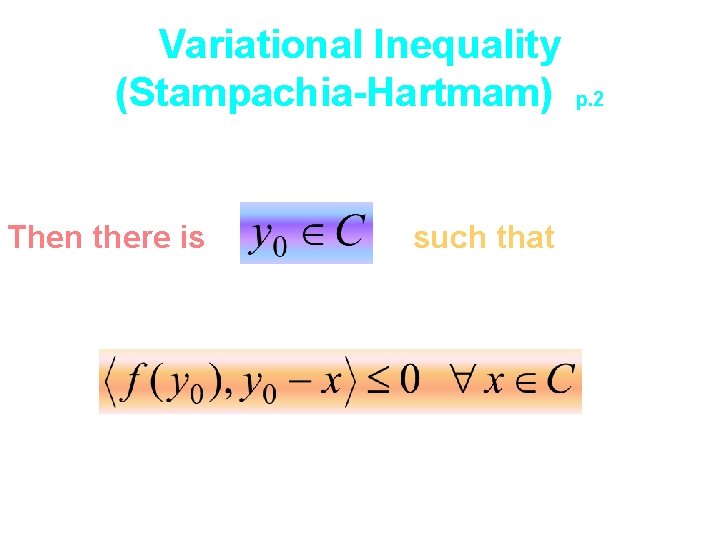
Variational Inequality (Stampachia-Hartmam) Then there is such that p. 2




Applications of Mazm. Orlich Theorem Inequality after mixing of functions

Theorem Let S be an arbitary set. The following two statements are equivalent:
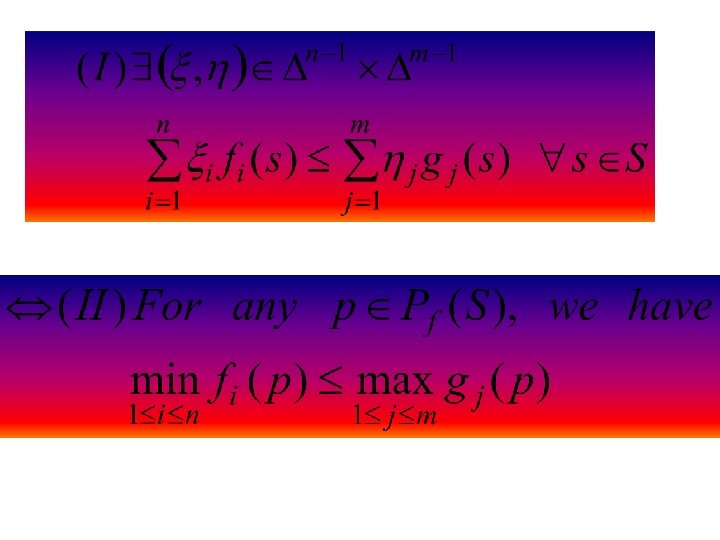
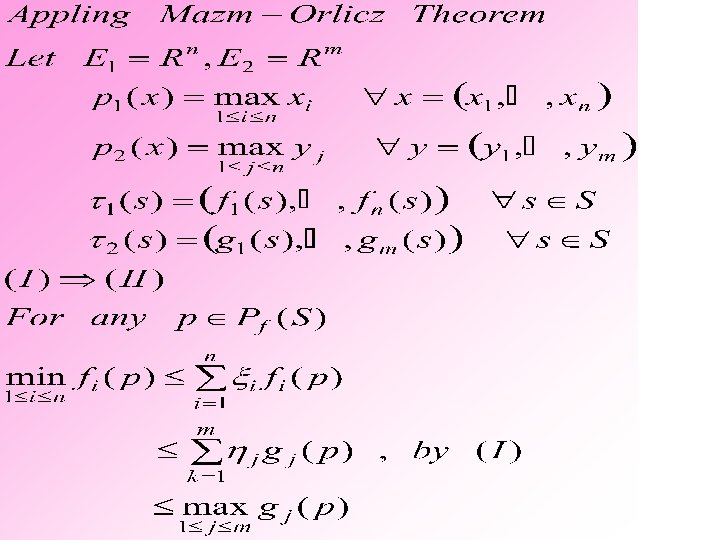





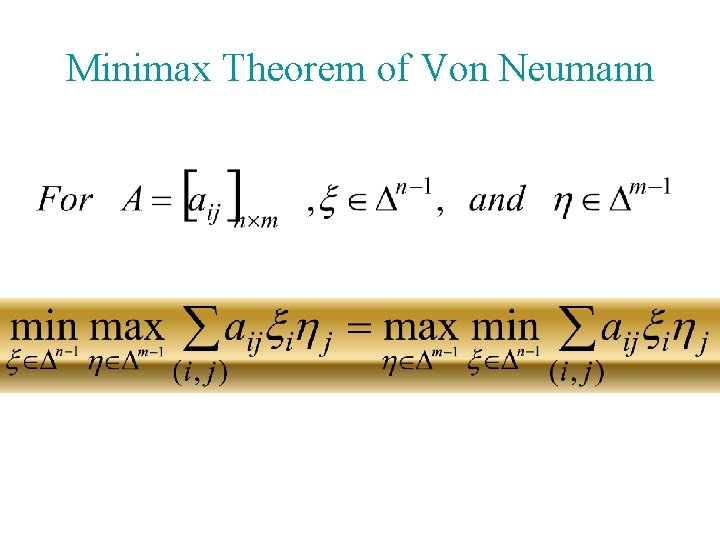
Minimax Theorem of Von Neumann





Lemma VI. 1 (Riesz-Lemma) Let For any fixed , apply Green’s second identity to u and then let in the domain we have

- Slides: 64