Applications of DensityFunctional Theory Structure Optimization Phase Transitions

Applications of Density-Functional Theory: Structure Optimization, Phase Transitions, and Phonons Christian Ratsch UCLA, Department of Mathematics In previous talks, we have learned how to calculate the ground state energy, and the forces between atoms. Now, we will discuss some important concepts and applications of what we can do with this.

Outline • Structure Optimization • Optimize bond length • Optimize atomic structure of a cluster or molecule • Optimize structure of a surface • Phase transitions • Phonons • Structural and vibrational properties of metal clusters • Dynamics on surfaces • Molecular dynamics • Use transition state theory: DFT can be used to calculate energy barriers, prefactors.

Structure optimization; example: Vanadium dimer F • Put atoms “anywhere” F F • Calculate forces F • Forces will move atoms toward configuration with lowest energy (forces = 0) Algorithms for structure optimization: • Damped Newton dynamics (option: NEWT) • Parameters l and m need to be optimized. • Quasi-Newton structure optimization (BFGS scheme; option: PORT) Hessian: • No parameters needed • In principle, only one iteration needed if Hessian is known, and fully harmonic. • In practise, a few iterations and Hessian updates are needed. • Nevertheless, this is typically the recommended option. My results for vanadium: lbond = 1. 80 Å (experimental value: 1. 77 Å) 1. 80 Å

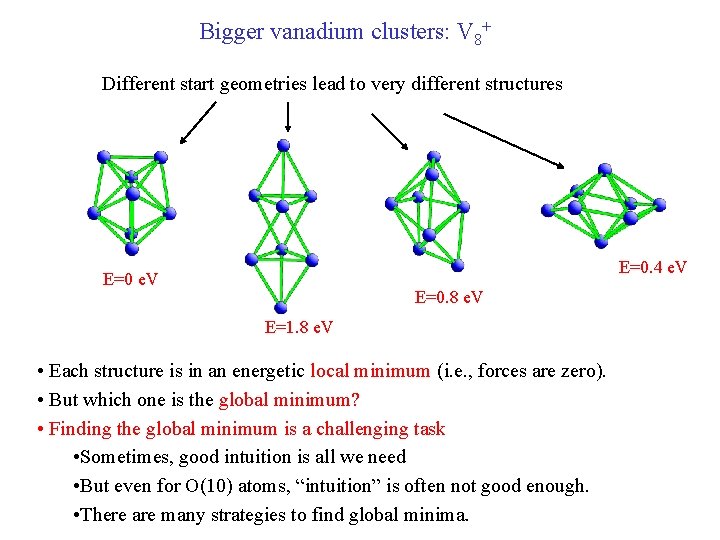
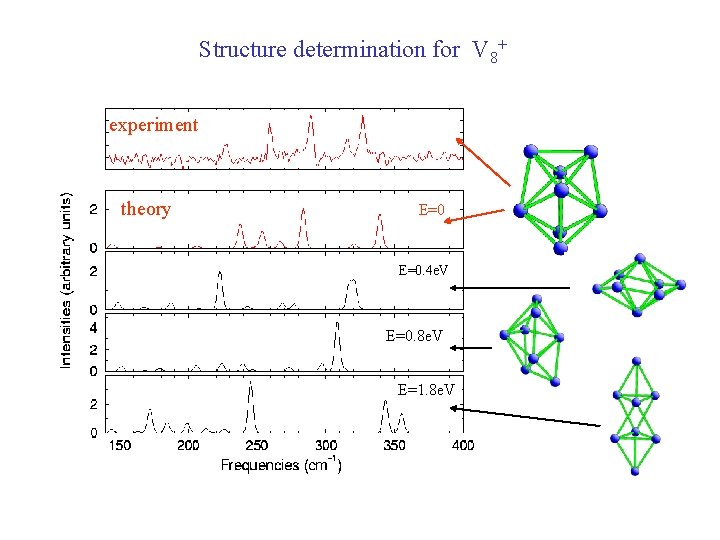
Bigger vanadium clusters: V 8+ Different start geometries lead to very different structures E=0. 4 e. V E=0. 8 e. V E=1. 8 e. V • Each structure is in an energetic local minimum (i. e. , forces are zero). • But which one is the global minimum? • Finding the global minimum is a challenging task • Sometimes, good intuition is all we need • But even for O(10) atoms, “intuition” is often not good enough. • There are many strategies to find global minima.

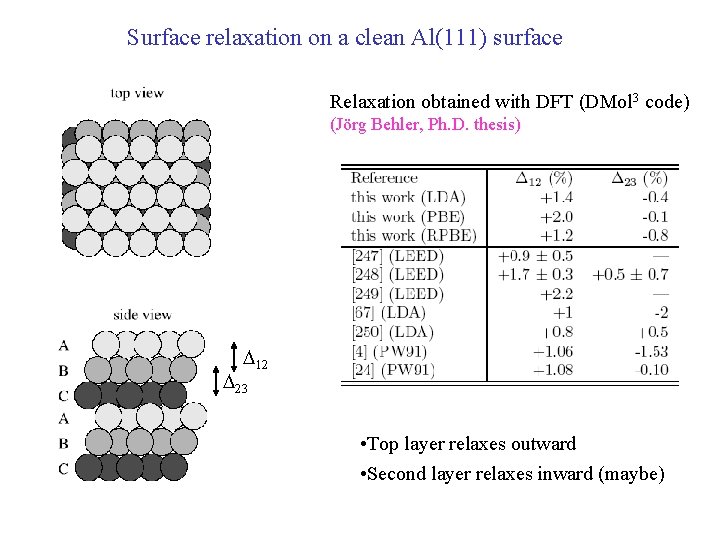
Surface relaxation on a clean Al(111) surface Relaxation obtained with DFT (DMol 3 code) (Jörg Behler, Ph. D. thesis) D 12 D 23 • Top layer relaxes outward • Second layer relaxes inward (maybe)

Things are more complicated on semiconductor surfaces • Semiconductor surfaces reconstruct. Example In. As(100) • Surface reconstruction is important for evolution of surface morphology which influences device properties • RHEED experiments show transition of symmetry from (4 x 2) to (2 x 4) In - terminated As - terminated [110] Which reconstruction ? Use density-functional theory (DFT)

Computation details of the DFT calculations • Computer code used: fhi 98 md • Norm-conserving pseudopotentials • Plane-wave basis set with Ecut = 12 Ryd • k summation: 64 k points per (1 x 1) cell • Local-density approximation (LDA) for exchange-correlation • Supercell with surface on one side, pseudo-hydrogen on the other side • Damped Newton dynamics to optimize atomic structure

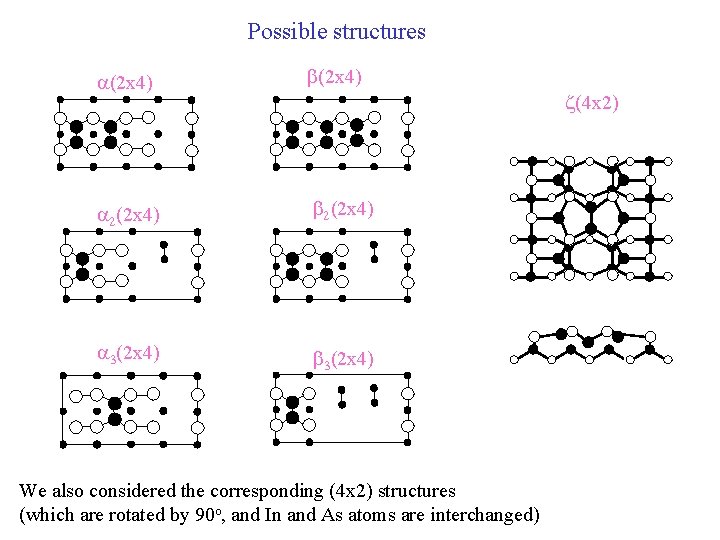
Possible structures a(2 x 4) b(2 x 4) a 2(2 x 4) b 2(2 x 4) a 3(2 x 4) b 3(2 x 4) z(4 x 2) We also considered the corresponding (4 x 2) structures (which are rotated by 90 o, and In and As atoms are interchanged)

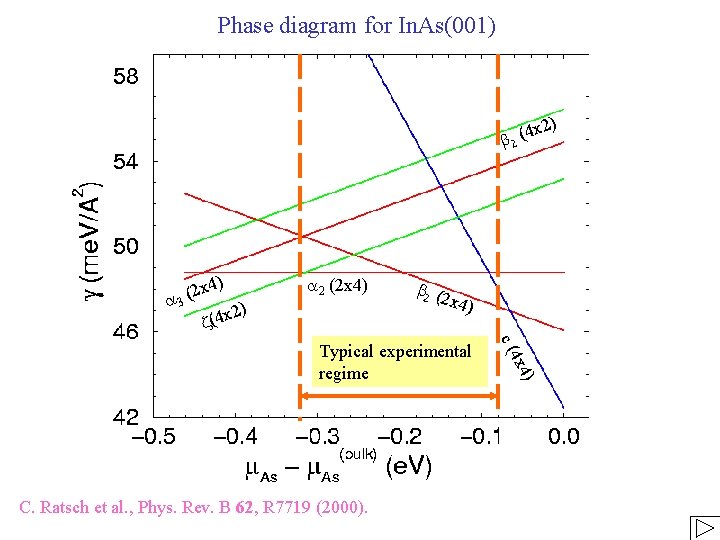
Phase diagram for In. As(001) ) 4 x 2 b 2 ( ) 2 x 4 ( a 3 2) x 4 ( z a 2 (2 x 4) b 2 ( 2 x 4 ) 4) 4 x C. Ratsch et al. , Phys. Rev. B 62, R 7719 (2000). c( Typical experimental regime

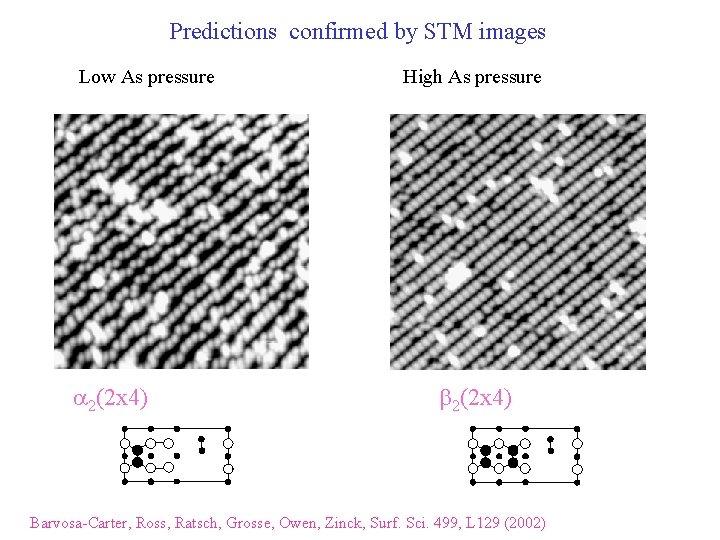
Predictions confirmed by STM images Low As pressure a 2(2 x 4) High As pressure b 2(2 x 4) Barvosa-Carter, Ross, Ratsch, Grosse, Owen, Zinck, Surf. Sci. 499, L 129 (2002)

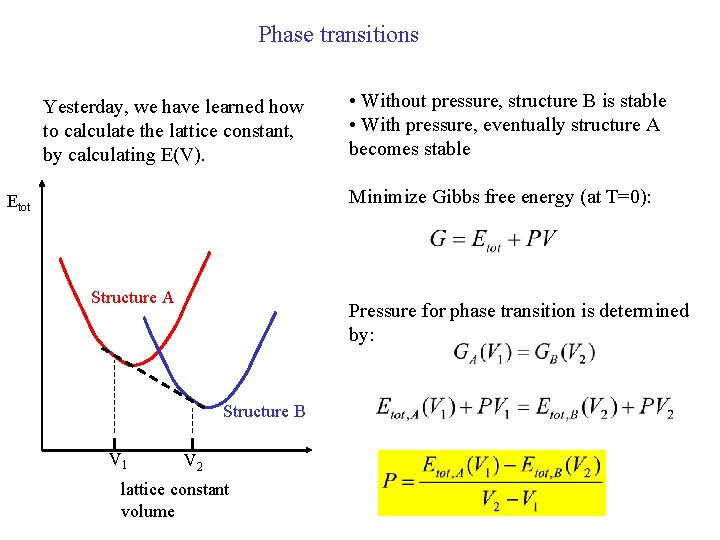
Phase transitions Yesterday, we have learned how to calculate the lattice constant, by calculating E(V). • Without pressure, structure B is stable • With pressure, eventually structure A becomes stable Minimize Gibbs free energy (at T=0): Etot Structure A Pressure for phase transition is determined by: Structure B V 1 V 2 lattice constant volume

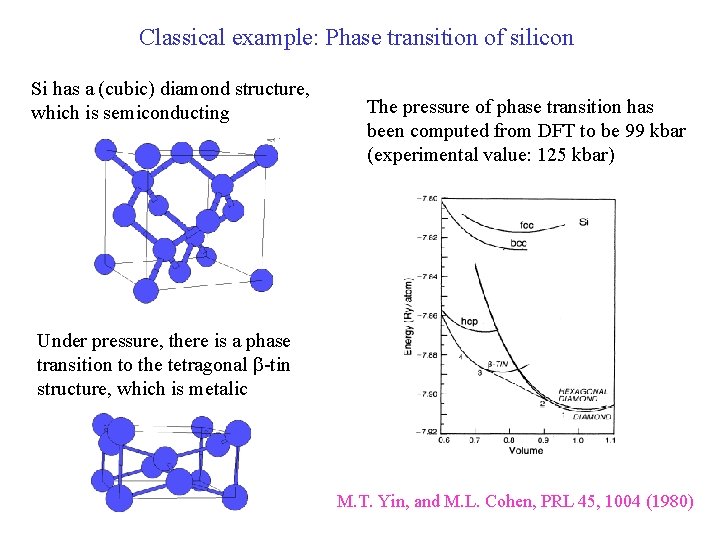
Classical example: Phase transition of silicon Si has a (cubic) diamond structure, which is semiconducting The pressure of phase transition has been computed from DFT to be 99 kbar (experimental value: 125 kbar) Under pressure, there is a phase transition to the tetragonal b-tin structure, which is metalic M. T. Yin, and M. L. Cohen, PRL 45, 1004 (1980)

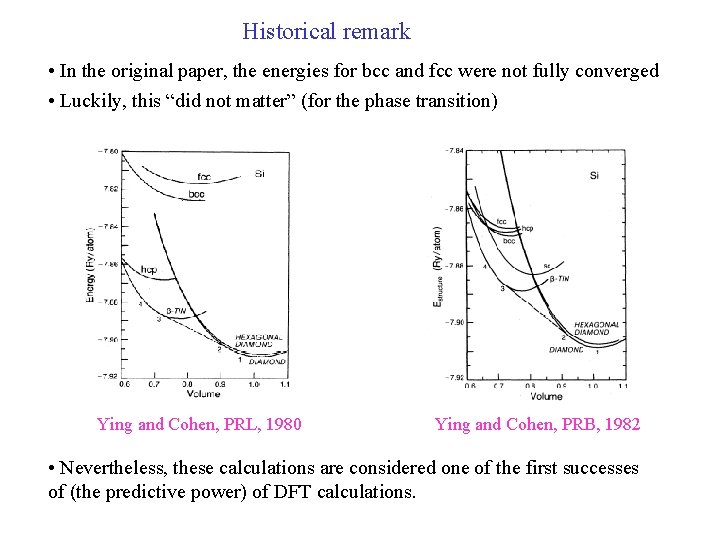
Historical remark • In the original paper, the energies for bcc and fcc were not fully converged • Luckily, this “did not matter” (for the phase transition) Ying and Cohen, PRL, 1980 Ying and Cohen, PRB, 1982 • Nevertheless, these calculations are considered one of the first successes of (the predictive power) of DFT calculations.

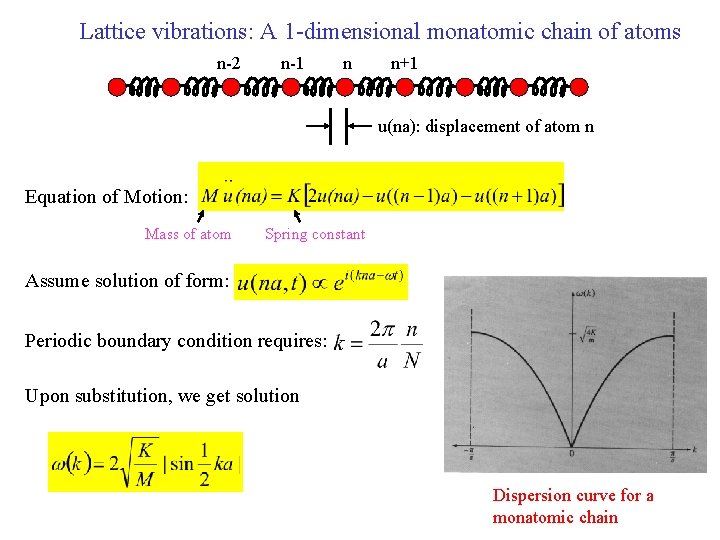
Lattice vibrations: A 1 -dimensional monatomic chain of atoms n-2 n-1 n n+1 n u(na): displacement of atom n Equation of Motion: Mass of atom Spring constant Assume solution of form: Periodic boundary condition requires: Upon substitution, we get solution Dispersion curve for a monatomic chain

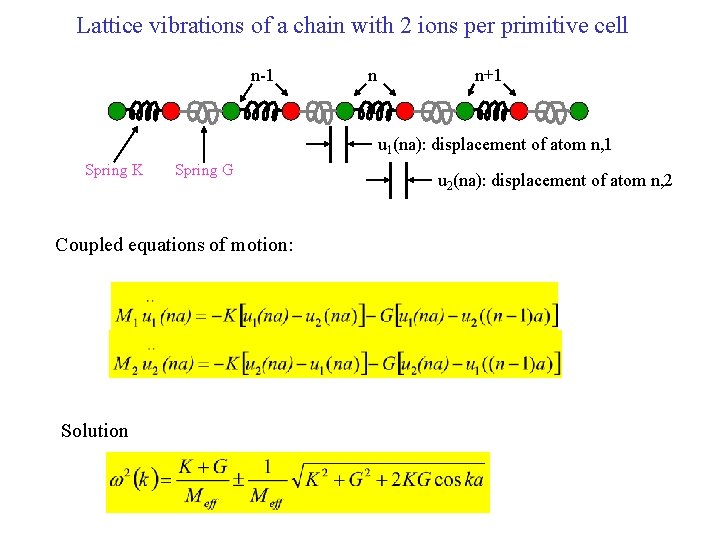
Lattice vibrations of a chain with 2 ions per primitive cell n-1 n n+1 n u 1(na): displacement of atom n, 1 Spring K Spring G Coupled equations of motion: Solution u 2(na): displacement of atom n, 2

Dispersion relation for the diatomic linear chain There are N values of k: • For each k, there are 2 solutions, leading to a total of 2 N normal modes. • The normal modes are also called “phonons”, in analogy to the term “photons”, since the energy of the N elastic modes are quantized as Optical branch Because long wavelength modes can interact with electromagnetic radiation Acoustic branch Because for small k, which is characteristic of sound waves

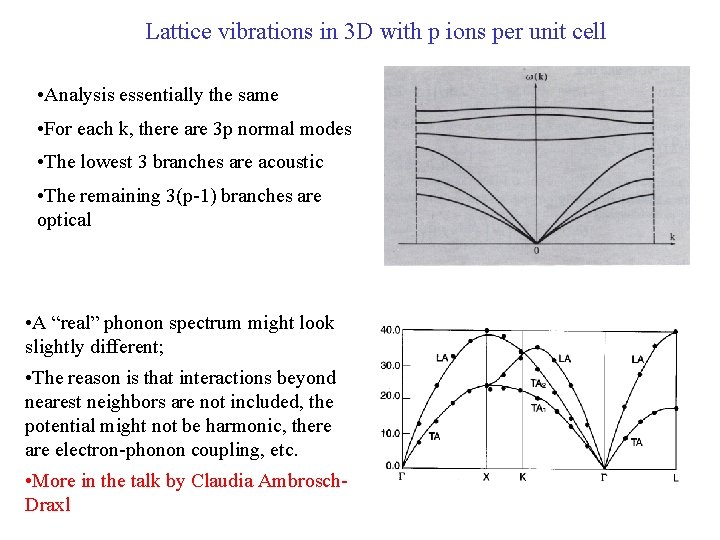
Lattice vibrations in 3 D with p ions per unit cell • Analysis essentially the same • For each k, there are 3 p normal modes • The lowest 3 branches are acoustic • The remaining 3(p-1) branches are optical • A “real” phonon spectrum might look slightly different; • The reason is that interactions beyond nearest neighbors are not included, the potential might not be harmonic, there are electron-phonon coupling, etc. • More in the talk by Claudia Ambrosch. Draxl

How can we calculate phonon spectrum? • Frozen phonon calculation • This is what you will do this afternoon. • DFT perturbation theory • Molecular Dynamics • Do an MD simulation for a sufficiently long time • “Measure” the time of vibrations; for example for dimer, this is obvious • For bigger systems, one needs to do Fourier analysis to do this • Very expensive

Frozen phonon calculations • Choose a supercell that corresponds to the inverse of wave vector k • Calculate dynamical matrix D • in principle, this is done by displacing each atom in each direction, and get the forces acting on all other atoms: p/3 a p/2 a p/a • eigenvalues l are the frequencies • in practise, one exploits the symmetry of the system (need group theory) • Repeat for several k • More details in the presentation by Mahboubeh Hortamani

Structural and vibrational properties of small vanadium clusters Why do we care about small metal clusters? • Many catalytic converters are based on clusters • Clusters will play a role in nano-electronics (quantum dots) • Importance in Bio-Chemistry • Small clusters (consisting of a few atoms) are the smallest nano-particles! This work was also motivated by interesting experimental results by A. Fielicke, G. v. -Helden, and G. Meijers (all FHI Berlin)

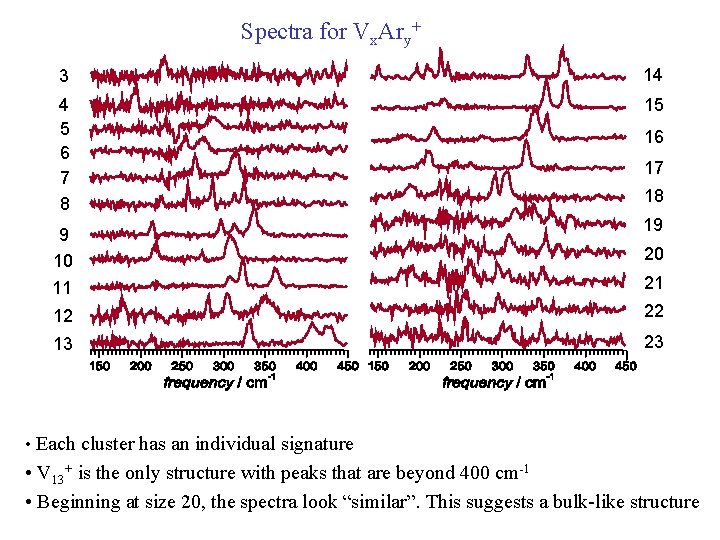
Spectra for Vx. Ary+ 3 14 4 5 6 7 8 15 9 10 11 16 17 18 19 20 21 12 22 13 23 • Each cluster has an individual signature • V 13+ is the only structure with peaks that are beyond 400 cm-1 • Beginning at size 20, the spectra look “similar”. This suggests a bulk-like structure

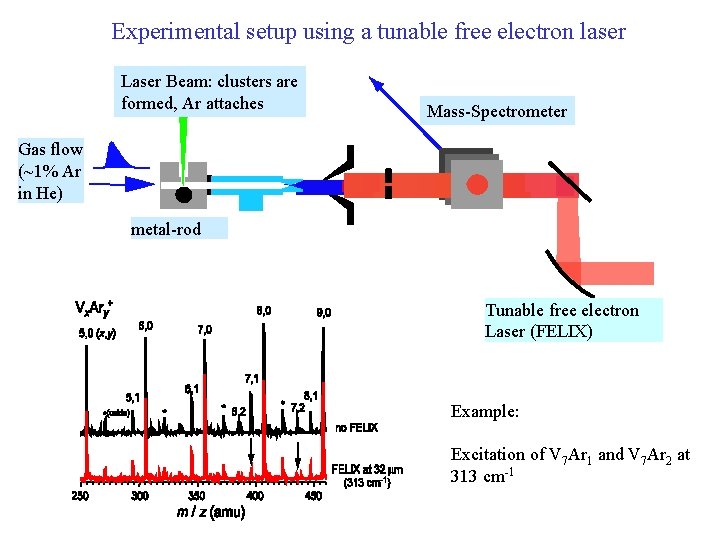
Experimental setup using a tunable free electron laser Laser Beam: clusters are formed, Ar attaches Mass-Spectrometer Gas flow (~1% Ar in He) metal-rod Tunable free electron Laser (FELIX) Example: Excitation of V 7 Ar 1 and V 7 Ar 2 at 313 cm-1

DFT calculations for small metal clusters • Computer Code used: DMol 3 • GGA for Exchange-Correlation (PBE); but we also tested and compared LDA, RPBE • We tested a large number of possible atomic structures, and spin states. • All atomic structures are fully relaxed. • Determine the energetically most preferred structures • Calculate the vibrational spectra with DFT (by diagonalizing force constant matrix, which is obtained by displacing each atom in all directions) • Calculate the IR intensities from derivative of the dipol moment What can we learn from these calculations? • Confirm the observed spectra • Determine the structure of the clusters • Is the spectrum the result of one or several isomers?

Structure determination for V 8+ experiment theory E=0. 4 e. V E=0. 8 e. V E=1. 8 e. V

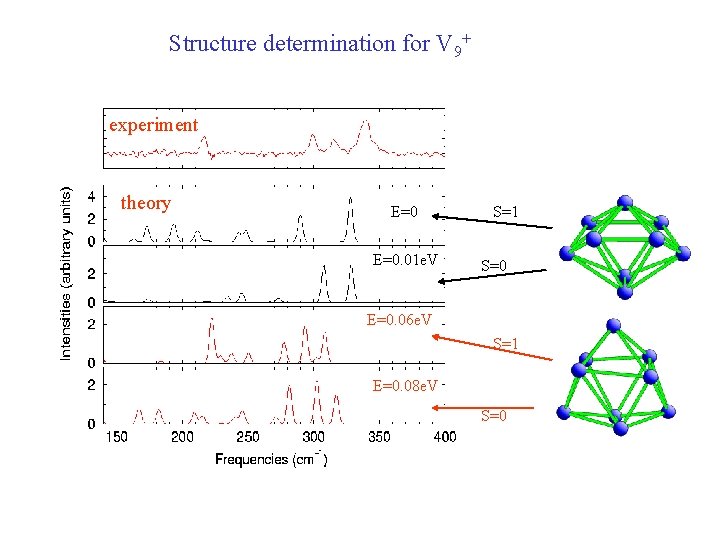
Structure determination for V 9+ experiment theory E=0. 01 e. V S=1 S=0 E=0. 06 e. V S=1 E=0. 08 e. V S=0

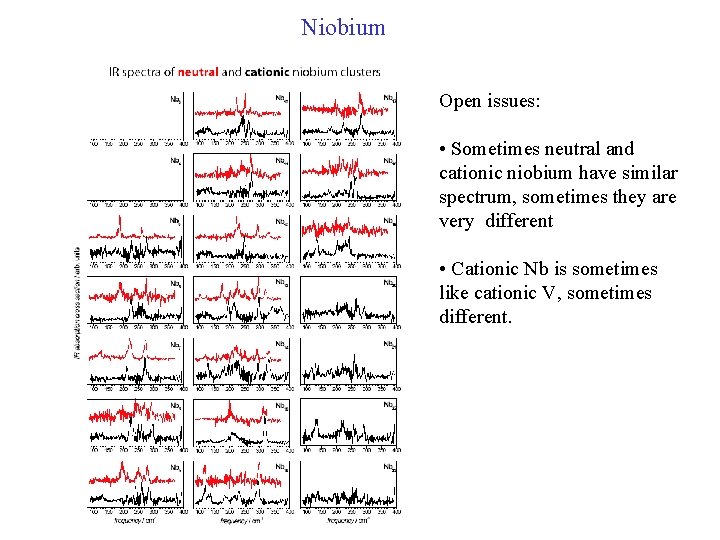
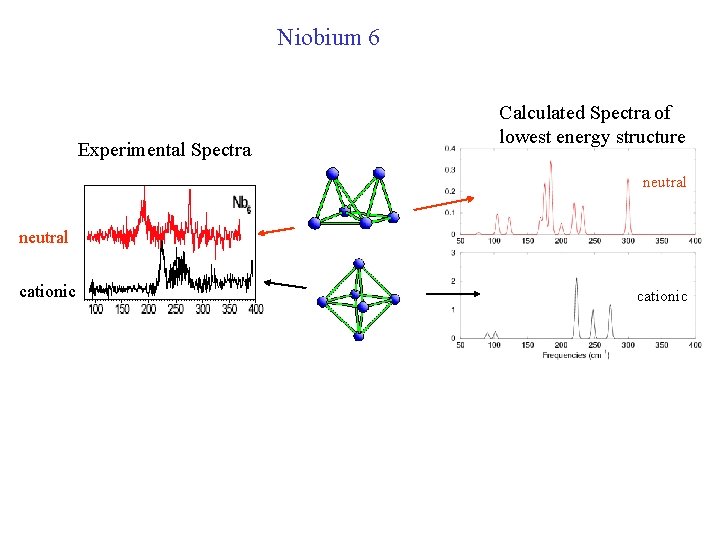
Niobium Open issues: • Sometimes neutral and cationic niobium have similar spectrum, sometimes they are very different • Cationic Nb is sometimes like cationic V, sometimes different.

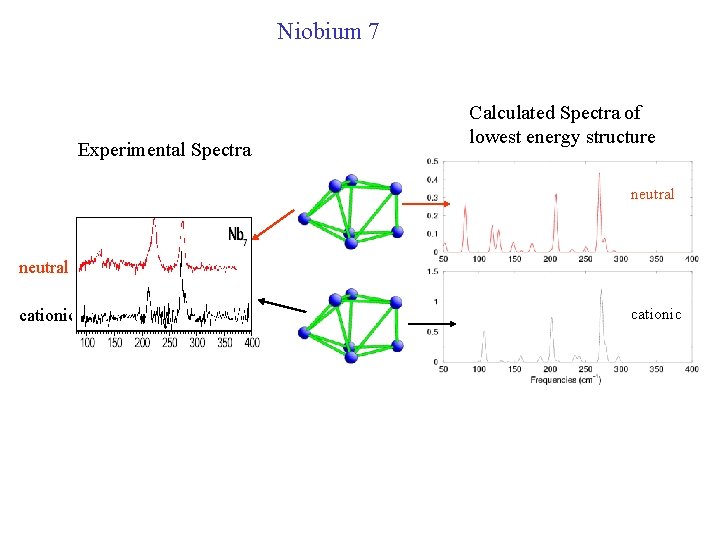
Niobium 7 Experimental Spectra Calculated Spectra of lowest energy structure neutral cationic

Niobium 6 Experimental Spectra Calculated Spectra of lowest energy structure neutral cationic

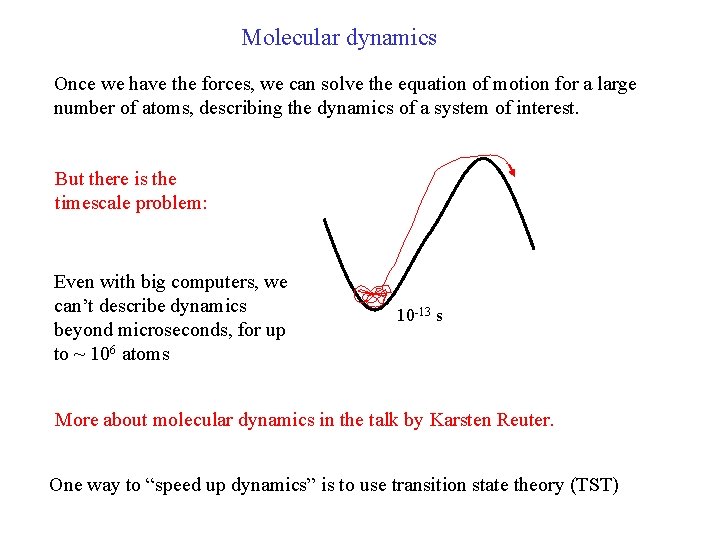
Molecular dynamics Once we have the forces, we can solve the equation of motion for a large number of atoms, describing the dynamics of a system of interest. But there is the timescale problem: Even with big computers, we can’t describe dynamics beyond microseconds, for up to ~ 106 atoms 10 -13 s More about molecular dynamics in the talk by Karsten Reuter. One way to “speed up dynamics” is to use transition state theory (TST)

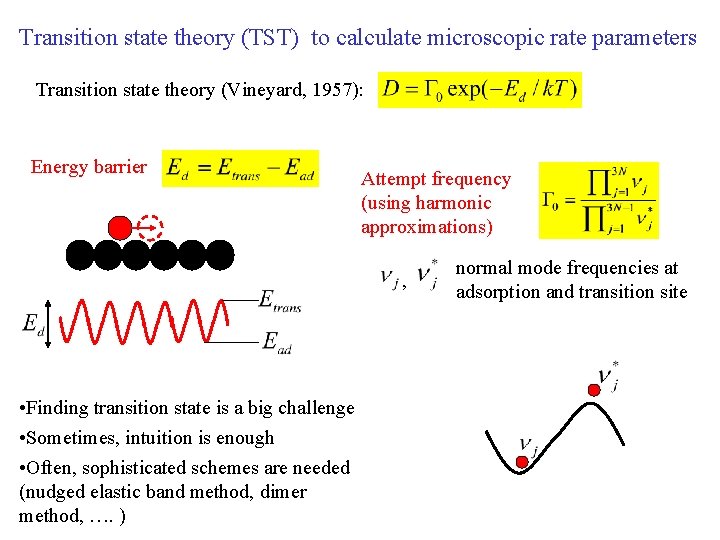
Transition state theory (TST) to calculate microscopic rate parameters Transition state theory (Vineyard, 1957): Energy barrier Attempt frequency (using harmonic approximations) , • Finding transition state is a big challenge • Sometimes, intuition is enough • Often, sophisticated schemes are needed (nudged elastic band method, dimer method, …. ) normal mode frequencies at adsorption and transition site

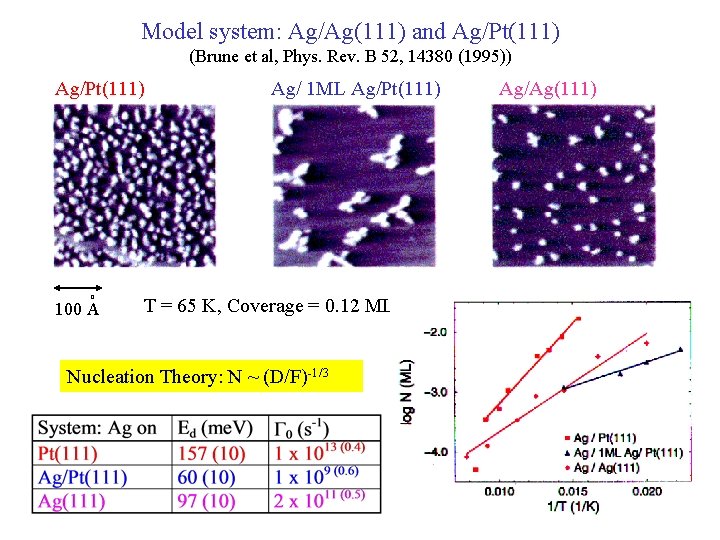
Model system: Ag/Ag(111) and Ag/Pt(111) (Brune et al, Phys. Rev. B 52, 14380 (1995)) Ag/Pt(111) o 100 A Ag/ 1 ML Ag/Pt(111) T = 65 K, Coverage = 0. 12 ML Nucleation Theory: N ~ (D/F)-1/3 Ag/Ag(111)

Results and comparison: Diffusion barrier • Tensile strain: less diffusion • Compressive strain: increased diffusion Lowered diffusion barrier for Ag on Ag/Pt(111) is mainly an effect of strain. Ratsch et al. , Phys. Rev. B 55, 6750 (1997)

How to calculate the prefactor Attempt frequency • Calculate force constant matrix by displacing each atom in x, y, z-direction, and by calculating the forces that act on all atoms • Eigenvalues of this matrix are the normal mode frequencies , • Important question: how many degrees of freedom need to be included? Convergence test for Ag/Ag(111) only adatom 2 x 2 cell adatom and top layer, 2 x 2 cell adatom and 2 layers, 4 x 4 cell # degrees of freedom 3 15 99 Prefactor G 0 (THz) 0. 82 0. 71 1. 55 Ratsch et al, Phys. Rev. B 58, 13163 (1998)

Results and comparison: Prefactor Compensation effect: • Prefactor is O(1 THz) for all systems Higher barrier • Compensation effect is not confirmed Higher prefactor • Explanation for experimental result: • Long range interactions are important for systems with small barrier (Fichthorn and Scheffler, PRL, 2000; Bogicevic et al. , PRL, 2000), • Simple nucleation theory does not apply any longer but can be modified (Venables, Brune, PRB 2002)

Conclusion and summary • DFT calculations can be used to optimize the atomic structure of a system • DFT calculations can be used to calculate the pressure of a phase transition. This will be part of the exercises this afternoon! • DFT calculations can be used to calculate a phonon spectrum. This will also be part of the exercises this afternoon. • DFT calculations can be used to obtain structural and vibrational properties of clusters • DFT calculations can be used to obtain the relevant microscopic parameters that describe the dynamics on surfaces.