Applications of Convex Restriction Techniques to Electric Power

Applications of Convex Restriction Techniques to Electric Power System Optimization Problems Dan Molzahn Georgia Tech ECE LANL Grid Science Winter School and Conference January 15, 2021

Collaborators • Dongchan Lee • Line Roald • Kostya Turitsyn Introduction 1 / 28

The Power Flow Equations • Model the relationships between the voltages and the power injections. Power flow equations Voltage phasors: • Central to many power system optimization and control problems. ‒ Optimal power flow, unit commitment, voltage stability, contingency analysis, transmission switching, etc. Introduction 2 / 28

Optimal Power Flow (OPF) Generation Cost Engineering Inequalities Power Flow Equalities (Reference Angle at the “Slack Bus”) Introduction 3 / 28

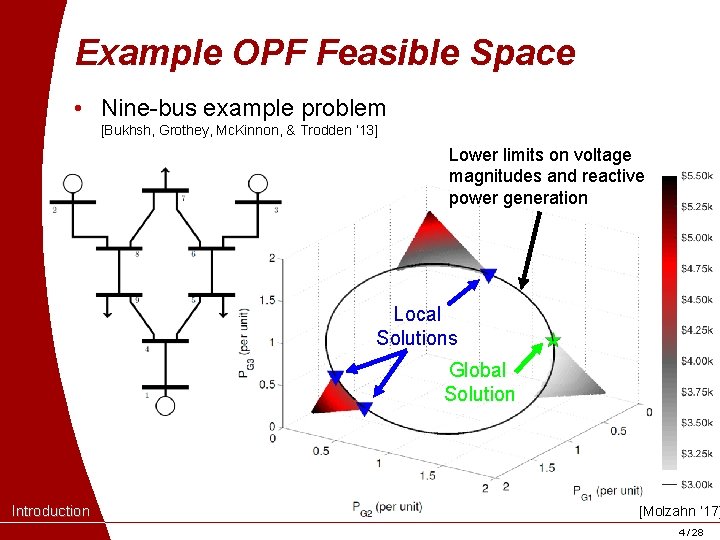
Example OPF Feasible Space • Nine-bus example problem [Bukhsh, Grothey, Mc. Kinnon, & Trodden ‘ 13] Lower limits on voltage magnitudes and reactive power generation Local Solutions Global Solution Introduction [Molzahn ’ 17] 4 / 28

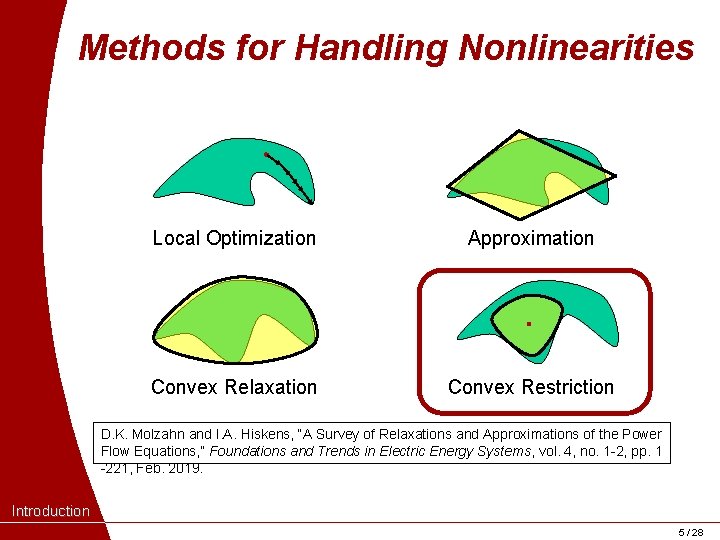
Methods for Handling Nonlinearities Local Optimization Approximation Convex Relaxation Convex Restriction D. K. Molzahn and I. A. Hiskens, “A Survey of Relaxations and Approximations of the Power Flow Equations, ” Foundations and Trends in Electric Energy Systems, vol. 4, no. 1 -2, pp. 1 -221, Feb. 2019. Introduction 5 / 28

Overview of Convex Restrictions D. Lee, H. D. Nguyen, K. Dvijotham, and K. Turitsyn, “Convex Restriction of Power Flow Feasibility Sets, ” IEEE Transactions on Control of Network Systems, vol. 6, no. 3, pp. 1235 -1245, Sept. 2019. 6 / 28

Convex Restrictions • Compute convex regions that are completely contained within the non-convex feasible space. • Construct around a feasible base point. Convex Restrictions [Yu, Nguyen & Turitsyn ‘ 15], [Dvijotham & Turitsyn ‘ 15], [Bolognani & Zampieri ‘ 16], [Simpson-Porco, Dörfler & Bullo ‘ 16], [Wang, Bernstein, Le Boudec & Paolone ‘ 17], [Dvijotham, Mallada & Simpson-Porco ‘ 18], [Dvijotham, Nguyen & Turitsyn ‘ 18], [Wang, Bernstein, Le Boudec, & Paolone ‘ 18], [Nguyen, Dvijotham & Turitsyn ‘ 19], [Cui & Sun ‘ 19], [Lee, Nguyen, Dvijotham, Turitsyn ‘ 19] 7 / 28

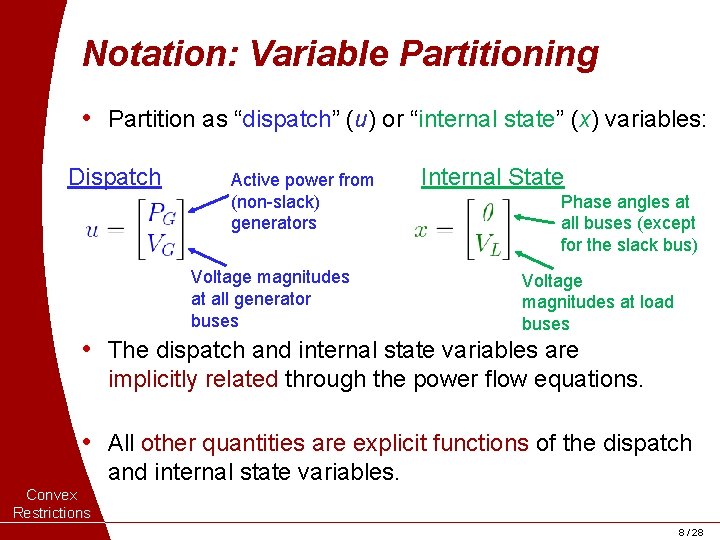
Notation: Variable Partitioning • Partition as “dispatch” (u) or “internal state” (x) variables: Dispatch Active power from (non-slack) generators Voltage magnitudes at all generator buses Internal State Phase angles at all buses (except for the slack bus) Voltage magnitudes at load buses • The dispatch and internal state variables are implicitly related through the power flow equations. • All other quantities are explicit functions of the dispatch and internal state variables. Convex Restrictions 8 / 28

Defining Convex Restrictions • What is a convex restriction for an optimization problem with nonlinear equality constraints? • Convex relaxation: Extend the feasible space. • Convex restriction: The interior is empty! Projection Find a convex region in for which there exists a feasible. • Challenge: How to handle inequalities that are functions of ? Incorporate into the projection. Convex Restrictions Slide adopted from Line Roald (INFORMS ‘ 19) 9 / 28

Deriving Convex Restrictions • Two-step process: 1. Write a fixed point formulation of the power flow equations: 2. Apply Brouwer’s Fixed Point Theorem: ‒ Self-mapping set of internal state variables. ‒ Concave envelopes enclosing nonlinearities. • Result: Convex quadratic constraints whose satisfaction guarantees the existence of a power flow solution satisfying all inequalities. Convex Restrictions 10 / 28

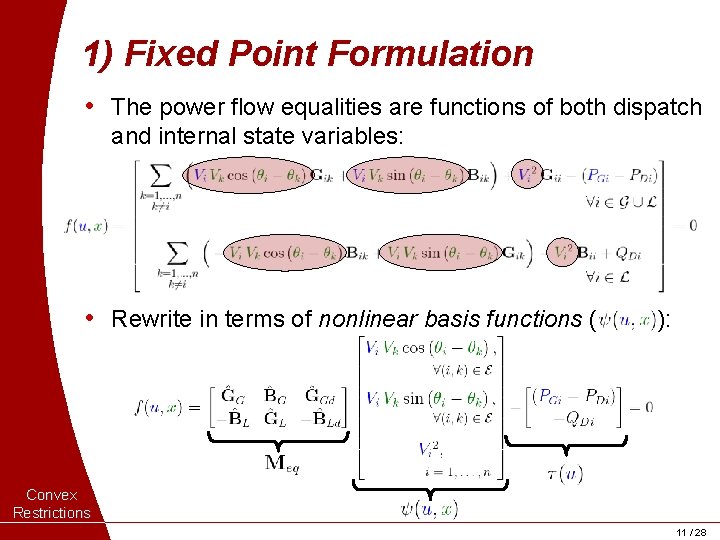
1) Fixed Point Formulation • The power flow equalities are functions of both dispatch and internal state variables: • Rewrite in terms of nonlinear basis functions ( ): Convex Restrictions 11 / 28

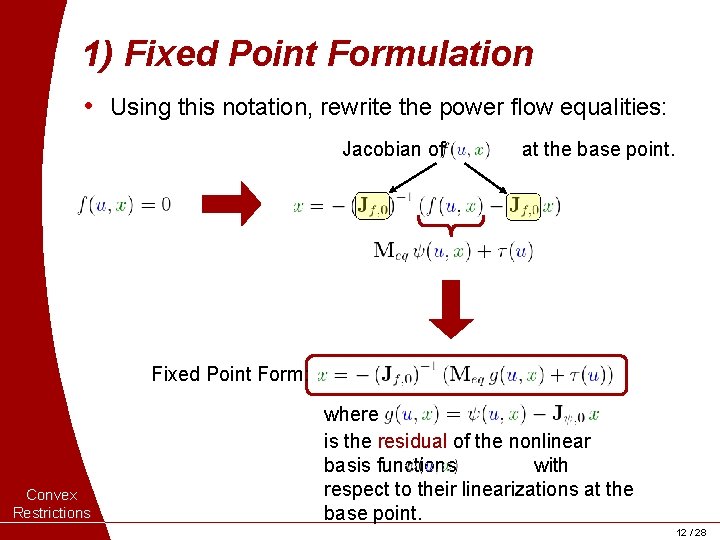
1) Fixed Point Formulation • Using this notation, rewrite the power flow equalities: Jacobian of at the base point. Fixed Point Form: Convex Restrictions where is the residual of the nonlinear basis functions with respect to their linearizations at the base point. 12 / 28

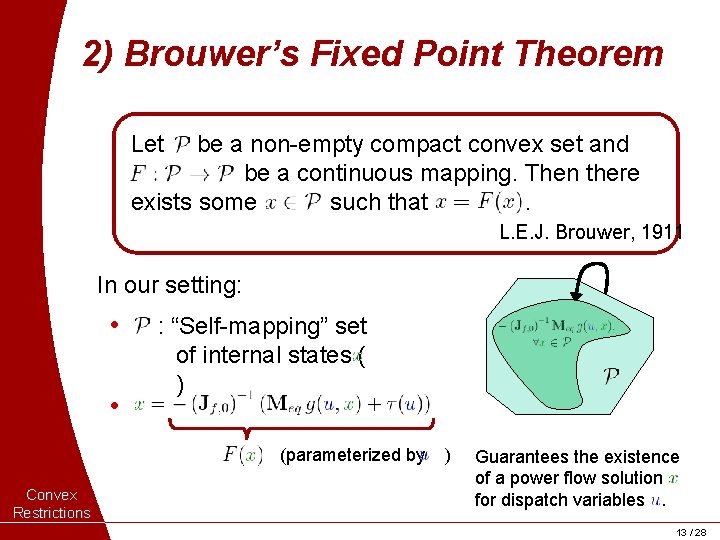
2) Brouwer’s Fixed Point Theorem Let be a non-empty compact convex set and be a continuous mapping. Then there exists some such that. L. E. J. Brouwer, 1911 In our setting: • • : “Self-mapping” set of internal states ( ) (parameterized by Convex Restrictions ) Guarantees the existence of a power flow solution for dispatch variables. 13 / 28

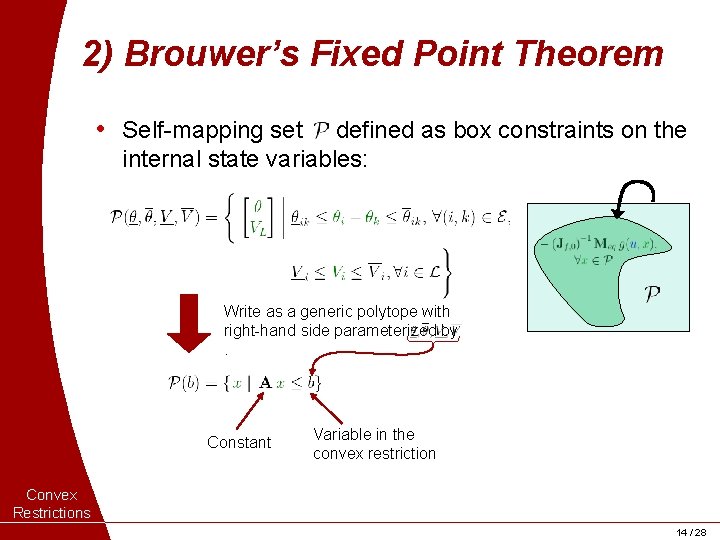
2) Brouwer’s Fixed Point Theorem • Self-mapping set defined as box constraints on the internal state variables: Write as a generic polytope with right-hand side parameterized by. Constant Variable in the convex restriction Convex Restrictions 14 / 28

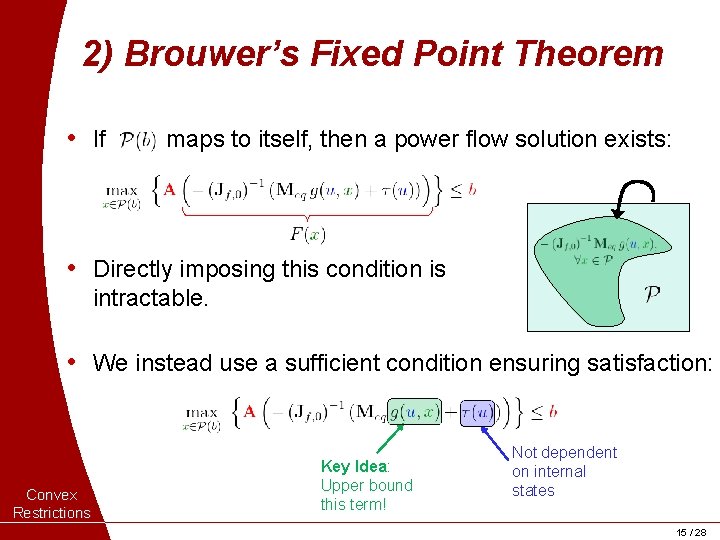
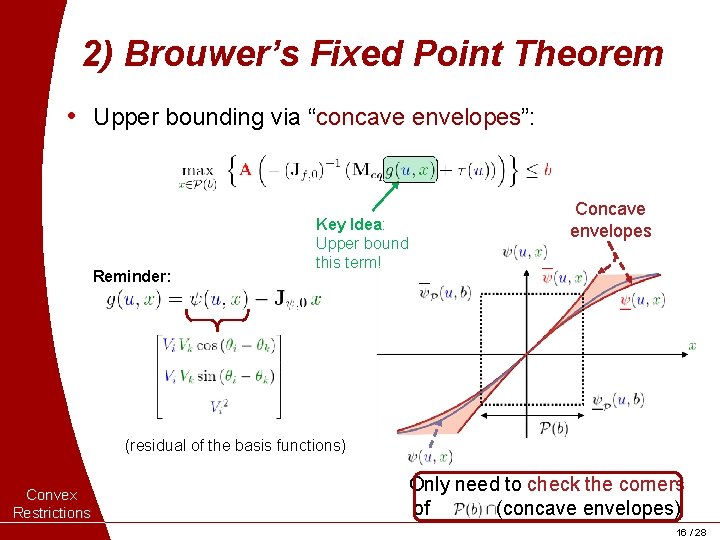
2) Brouwer’s Fixed Point Theorem • If maps to itself, then a power flow solution exists: • Directly imposing this condition is intractable. • We instead use a sufficient condition ensuring satisfaction: Convex Restrictions Key Idea: Upper bound this term! Not dependent on internal states 15 / 28

2) Brouwer’s Fixed Point Theorem • Upper bounding via “concave envelopes”: Reminder: Key Idea: Upper bound this term! Concave envelopes (residual of the basis functions) Convex Restrictions Only need to check the corners of (concave envelopes) 16 / 28

Putting It All Together Dependent on the base point. Self-mapping condition existence of a power flow solution Power flow solution satisfies inequalitie where and arguments. Convex Restrictions take the positive and negative parts of their Convex quadratically constrained quadratic program! Number of constraints scales linearly with the system size. 17 / 28

Example Convex Restriction OPF Feasible Space Convex Restriction Base Point Convex restriction for a modified IEEE 9 -bus test case Convex Restrictions D. Lee, H. D. Nguyen, K. Dvijotham, and K. Turitsyn, “Convex Restriction of Power Flow Feasibility Sets, ” IEEE Transactions on Control of Network Systems, vol. 6, no. 3, pp. 1235 -1245, Sept. 2019. 18 / 28

Applications of Convex Restrictions: 1) Feasible Path Identification D. Lee, K. Turitsyn, D. K. Molzahn, and L. A. Roald “Feasible Path Identification in Optimal Power Flow with Sequential Convex Restriction, ” IEEE Transactions on Power Systems, vol. 35, no. 5, pp. 3648 -3659, Sept. 2020. 2) Robust Optimal Power Flow 19 / 28

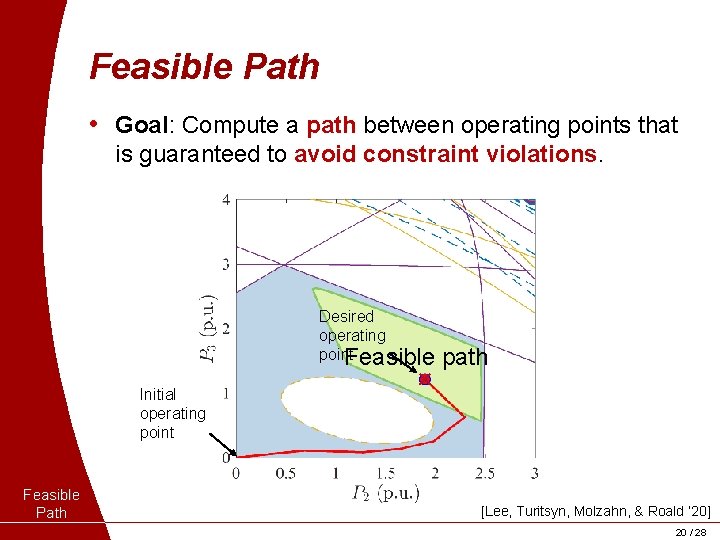
Feasible Path • Goal: Compute a path between operating points that is guaranteed to avoid constraint violations. Desired operating Infeasible path point Feasible path Initial operating point Feasible Path [Lee, Turitsyn, Molzahn, & Roald ’ 20] 20 / 28

Applications of Convex Restrictions: 1) Feasible Path Identification 2) Robust Optimal Power Flow D. Lee, K. Turitsyn, D. K. Molzahn, and L. A. Roald “Robust AC Optimal Power Flow with Robust Convex Restriction, ” ar. Xiv: 2005. 04835, 2020. 21 / 28

Problem Overview How to dispatch the generators such that the system is robust to any realization within a specified uncertainty set? • Other stochastic approaches for power system optimization: Robust OPF [Capitanescu, Fliscounakis, Panciatici & Wehenkel ‘ 12], [Vrakopoulou, Katsampani, Margellos, Lygeros & Andersson ‘ 13], [Phan & Ghosh ‘ 14], [Nasri, Kazempour, Conejo & Ghandhari ‘ 16], [Venzke, Halilbasic, Markovic, Hug & Chaitzivasileiadis ‘ 18], [Roald, Molzahn & Tobler ‘ 17], [Roald & Andersson ‘ 18], [Marley, Vrakopoulou & Hiskens ‘ 17], [Lorca & Sun ‘ 18], [Molzahn & Roald ‘ 18], [Louca & Bitar ‘ 19] 22 / 28

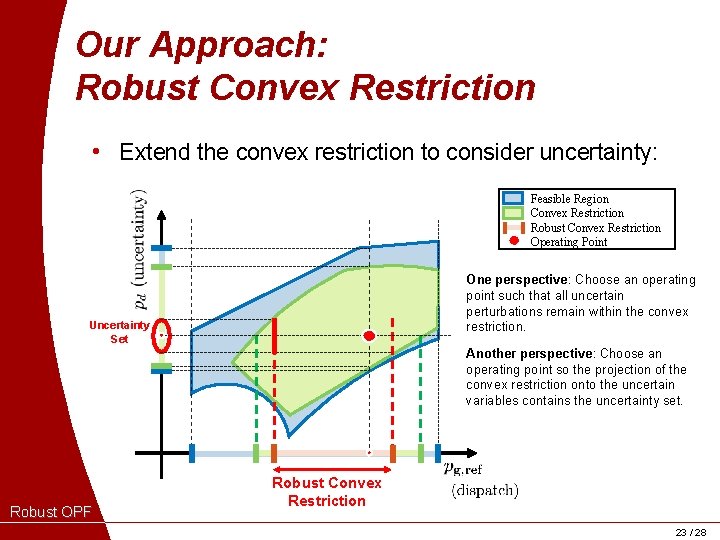
Our Approach: Robust Convex Restriction • Extend the convex restriction to consider uncertainty: Feasible Region Convex Restriction Robust Convex Restriction Operating Point One perspective: Choose an operating point such that all uncertain perturbations remain within the convex restriction. Uncertainty Set Another perspective: Choose an operating point so the projection of the convex restriction onto the uncertain variables contains the uncertainty set. Robust OPF Robust Convex Restriction 23 / 28

Our Approach: Robust Convex Restriction • Extend the convex restriction to consider uncertainty: Key idea: Upper bound the impact of the uncertainty. Analytic solution dependent on the uncertainty set parameters: • Solve iteratively, updating the base point at each iteration. • Resulting operating points are guaranteed to be robustly Robust OPF feasible. (Only known algorithm with this guarantee!) 24 / 28

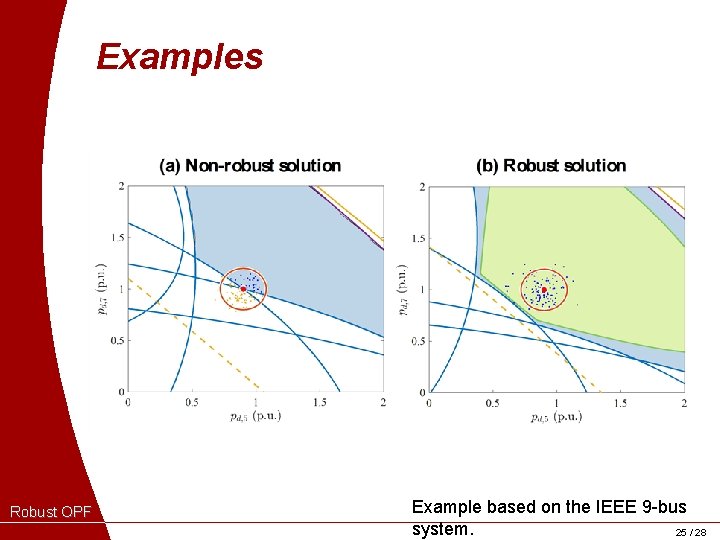
Examples Robust OPF Example based on the IEEE 9 -bus system. 25 / 28

Examples • Larger uncertainty sets push the solution further away from the boundary. Robust OPF Example based on the IEEE 9 -bus system. 26 / 28

Conclusions • Convex restrictions are powerful tools for ensuring feasibility while remaining tractable. ‒ Convex quadratically constrained quadratic programs that can be handled by for mature commercial solvers. • Applications include: ‒ Computing feasible paths between operating points. ‒ Solving robust optimal power flow with feasibility guarantees regarding both the power flow equalities and the engineering inequalities. (First algorithm capable of doing so for general system models!) Conclusion 27 / 28

Questions? Dan Molzahn Dongchan Lee molzahn@gatech. ed u dclee@mit. edu Line Roald roald@wisc. edu Kostya Turitsyn 28 / 28

References (1/2) J. Apt and A. Curtright, “The Spectrum of Power from Utility-Scale Wind Farms and Solar Photovoltaic Arrays, ” CEIC-08 -04, https: //ceic. tepper. cmu. edu/publications/working-papers S. Bolognani and S. Zampieri, "On the Existence and Linear Approximation of the Power Flow Solution in Power Distribution Networks", IEEE Transactions on Power Systems, vol. 31, no. 1, pp. 163 -172, Jan. 2016. F. Capitanescu, S. Fliscounakis, P. Panciatici, and L. Wehenkel, “Cautious Operation Planning Under Uncertainties, ” IEEE Transactions on Power Systems, vol. 27, no. 4, pp. 1859 -1869, Nov. 2012. W. A. Bukhsh, A. Grothey, K. I. Mc. Kinnon, and P. A. Trodden, “Local Solutions of the Optimal Power Flow Problem, ” IEEE Transactions on Power Systems, vol. 28, no. 4, pp. 4780 -4788, 2013. K. Dvijotham, E. Mallada and J. W. Simpson-Porco, "High-Voltage Solution in Radial Power Networks: Existence properties and equivalent algorithms", IEEE Control Systems Letters, vol. 1, no. 2, pp. 322 -327, Oct. 2017. K. Dvijotham, H. D. Nguyen and K. S. Turitsyn, "Solvability Regions of Affinely Parameterized Quadratic Equations", IEEE Control Systems Letters, vol. 2, no. 1, pp. 25 -30, Jan. 2018. K. Dvijotham and K. S. Turitsyn, "Construction of Power Flow Feasibility Sets", ar. Xiv: 1506. 07191, 2015. Energy Information Agency, “Annual Electricity Sales (Consumption), Revenue, Prices & Customers, ” https: //www. eia. gov/electricity/annual/xls/epa_02_02. xlsx K. H. La. Commare and J. H. Eto. “Cost of Power Interruptions to Electricity Consumers in the United States (US). " Energy, vol. 31, no. 12 pp. 1845 -1855, 2006. D. Lee, K. Turitsyn, D. K. Molzahn, and L. A. Roald “Feasible Path Identification in Optimal Power Flow with Sequential Convex Restriction, ” IEEE Transactions on Power Systems, vol. 35, no. 5, pp. 3648 -3659, Sept. 2020. D. Lee, K. Turitsyn, D. K. Molzahn, and L. A. Roald “Robust AC Optimal Power Flow with Robust Convex Restriction, ” ar. Xiv: 2005. 04835, 2020. A. Lorca and X. A. Sun, “The Adaptive Robust Multi-Period Alternating Current Optimal Power Flow Problem, ” IEEE Transactions on Power Systems, vol. 33, no. 2, pp. 1993 -2003, March 2018. R. Louca and E. Bitar, “Robust AC Optimal Power Flow, ” IEEE Transactions on Power Systems, vol. 34, no. 3, pp. 1669 -1681, May 2019. J. F. Marley, M. Vrakopoulou, and I. A. Hiskens, “Towards the Maximization of Renewable Energy Integration Using a Stochastic AC-QP Optimal Power Flow Algorithm, ” 10 th IREP Symposium on Bulk Power Systems Dynamics and Control, Aug. 2017. D. K. Molzahn, "Computing the Feasible Spaces of Optimal power Flow Problems, " IEEE Transactions on Power Systems, vol. 32, no. 6, pp. 4752 -4763, November 2017. References D. K. Molzahn and I. A. Hiskens, “A Survey of Relaxations and Approximations of the Power Flow Equations, ” Foundations and Trends in Electric Energy Systems, vol. 4, no. 1 -2, pp. 1 -221, Feb. 2019. 29 / 28

References (2/2) D. K. Molzahn and I. A. Hiskens, "Convex Relaxations of Optimal Power Flow Problems: An Illustrative Example, " IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 63, no. 5, pp. 650 -660, May 2016. D. K. Molzahn and L. A. Roald, “Towards an AC Optimal Power Flow Algorithm with Robust Feasibility Guarantees, ” 20 th Power Systems Computation Conference (PSCC), June 2018. A. Nasri, S. J. Kazempour, A. J. Conejo, and M. Ghandhari, “Network-Constrained AC Unity Commitment Under Uncertainty: A Benders’ Decomposition Approach, ” IEEE Transactions on Power Systems, vol. 31, no. 1, pp. 412 -422, Jan. 2016. H. D. Nguyen, K. Dvijotham and K. S. Turitsyn, "Constructing Convex Inner Approximations of Steady-State Security Regions", IEEE Transactions on Power Systems, vol. 34, no. 1, pp. 257 -267, Jan. 2019. D. Phan and S. Ghosh, “Two-Stage Stochastic Optimization for Optimal Power Flow Under Renewable Generation Uncertainty, ” ACM Transactions on Modeling and Computer Simulation, vol. 24, no. 1, pp. 2: 1 -2: 22, Jan. 2014. L. A. Roald and G. Andersson, “Chance-Constrained AC Optimal Power Flow: Reformulations and Efficient Algorithms, ” IEEE Transactions on Power Systems, vol. 33, no. 3, pp. 2906 -2918, May 2018. L. A. Roald, D. K. Molzahn, and A. F. Tobler, “Power System Optimization with Uncertainty and AC Power Flow: Analysis of an Iterative Algorithm, ” 10 th IREP Symposium on Bulk Power Systems Dynamics and Control, Aug. 2017. J. W. Simpson-Porco, F. Dörfler and F. Bullo, "Voltage Collapse in Complex Power Grids", Nature Communications, vol. 7, 2016. J. W. Simpson-Porco, "A Theory of Solvability for Lossless Power Flow Equations–Part I: Fixed-Point Power Flow", IEEE Trans. Control Netw. Syst. , vol. 5, no. 3, pp. 1361 -1372, Sept. 2018. A. Venzke, L. Halilbasic, U. Markovic, G. Hug, and S. Chatzivasileiadis, “Convex Relaxations of Chance Constraints AC Optimal Power Flow, ” IEEE Transactions on Power Systems, vol. 33, no. 3, pp. 2829 -2841, May 2018. M. Vrakopoulou, M. Katsampani, K. Margellos, J. Lygeros, and G. Andersson, “Probabilistic Security-Constrained AC Optimal Power Flow, ” IEEE Grenoble Power. Tech, June 2013. C. Wang, A. Bernstein, J. -Y. Le Boudec, and M. Paolone, "Existence and Uniqueness of Load-Flow Solutions in Three-Phase Distribution Networks", IEEE Transactions on Power Systems, vol. 32, no. 4, pp. 3319 -3320, July 2017. C. Wang, A. Bernstein, J. -Y. L. Boudec, and M. Paolone, “Explicit Conditions on Existence and Uniqueness of Load-Flow Solutions in Distribution Networks, ” IEEE Transactions on Smart Grid, vol. 9, no. 2, pp. 953 -962, March 2018. S. Yu, H. D. Nguyen, and K. S. Turitsyn, "Simple Certificate of Solvability of Power Flow Equations for Distribution Systems", IEEE Power & Energy Society General Meeting, 2015. References 30 / 28