Applications of addition theorem and superposition technique to

Applications of addition theorem and superposition technique to problems with circular boundaries subject to concentrated forces and screw dislocations Reporter: Chou K. H. Advisor: Chen J. T. Date: 2008/07/11 Place: HR 2 307 1

Outline Motivation and literature review l Derivation of the Green’s function l Superposition technique ¡ Addition theorem and boundary density ¡ Adaptive observer system ¡ Linear algebraic equation ¡ l Numerical examples Green’s function for the concentrated force problems ¡ Green’s function for the screw dislocation problems ¡ l Conclusions 2

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ ¡ l Numerical examples ¡ ¡ l Superposition technique Addition theorem for the kernel decomposition Fourier expansion for the boundary density Adaptive observer system Linear algebraic equation Green’s function for the concentrated force problems Green’s function for the screw dislocation problems Conclusions 3

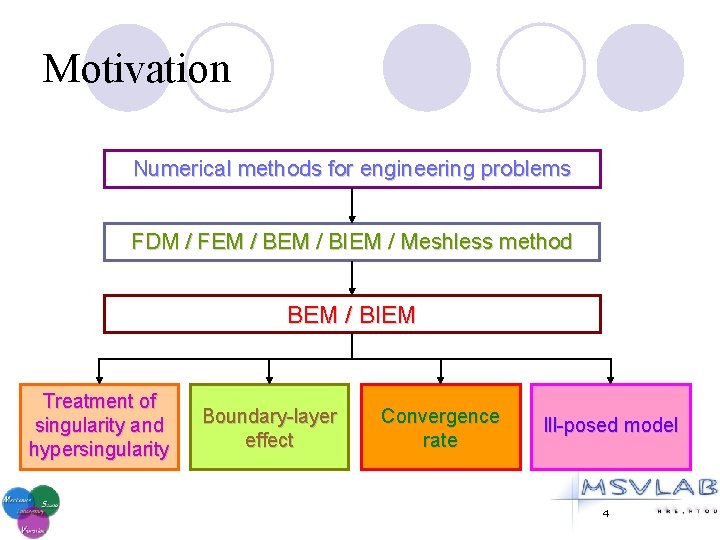
Motivation Numerical methods for engineering problems FDM / FEM / BIEM / Meshless method BEM / BIEM Treatment of singularity and hypersingularity Boundary-layer effect Convergence rate Ill-posed model 4

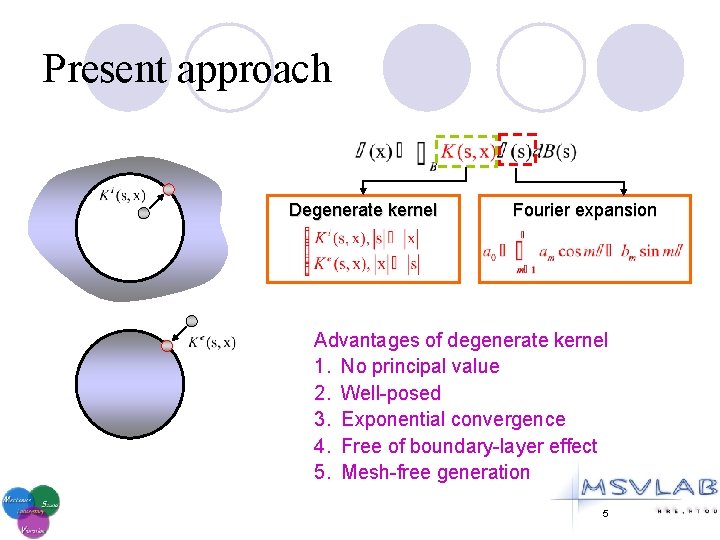
Present approach Degenerate kernel Fourier expansion Advantages of degenerate kernel 1. No principal value 2. Well-posed 3. Exponential convergence 4. Free of boundary-layer effect 5. Mesh-free generation 5

Literature review l. Laplace problem [Chen, Shen and Wu, 2005] l. Helmholtz problem [Chen, Chen and Chen, 2007] lbiharmonic problem [Chen, Hsiao and Leu, 2006] lanti-plane piezoelectricity problem [Chen and Wu, 2006] l. Green’s function for Laplace [Chen, Ke and Liao, 2008], Helmholtz [Chen and Ke, 2008] and biharmonic problems [Chen and Liao, 2008] l. Green’s function for the screw dislocation problem (present work) 6

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ ¡ l Numerical examples ¡ ¡ l Superposition technique Addition theorem for the kernel decomposition Fourier expansion for the boundary density Adaptive observer system Linear algebraic equation Green’s function for the concentrated force problems Green’s function for the screw dislocation problems Conclusions 7

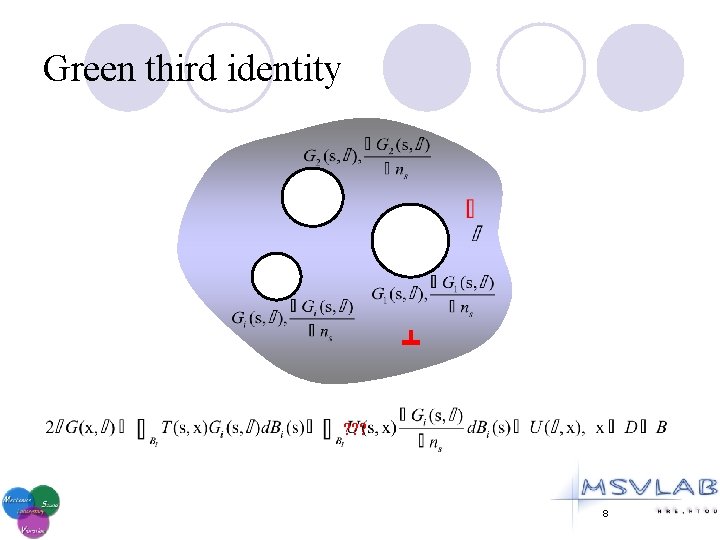
Green third identity ? ? ? 8

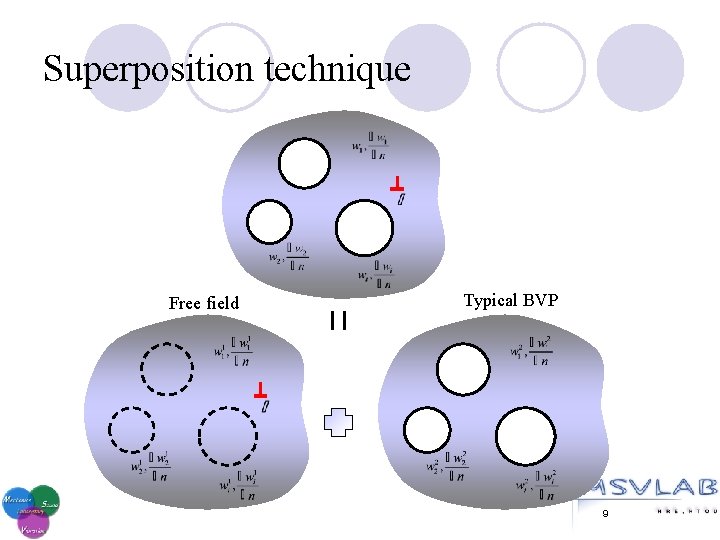
Superposition technique Free field Typical BVP 9

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ ¡ l Numerical examples ¡ ¡ l Superposition technique Addition theorem for the kernel decomposition Fourier expansion for the boundary density Adaptive observer system Linear algebraic equation Green’s function for the concentrated force problems Green’s function for the screw dislocation problems Conclusions 10

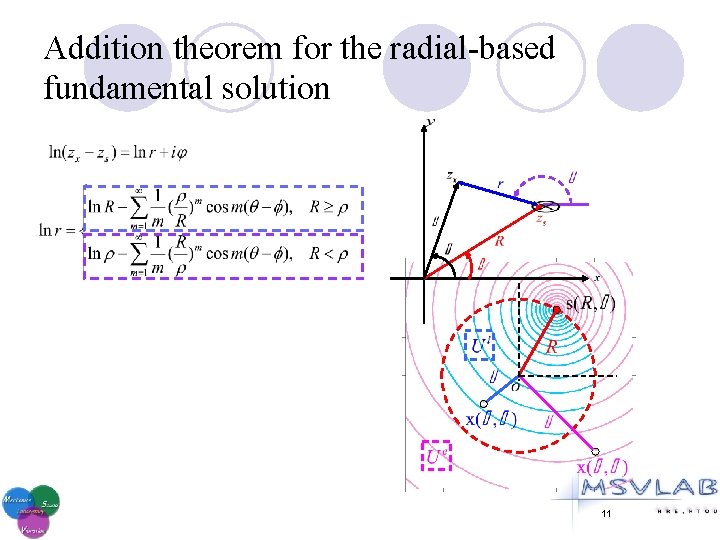
Addition theorem for the radial-based fundamental solution 11

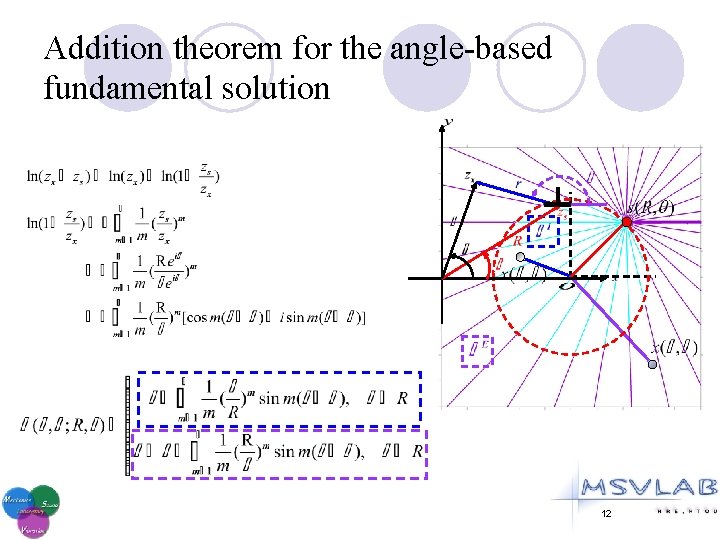
Addition theorem for the angle-based fundamental solution 12

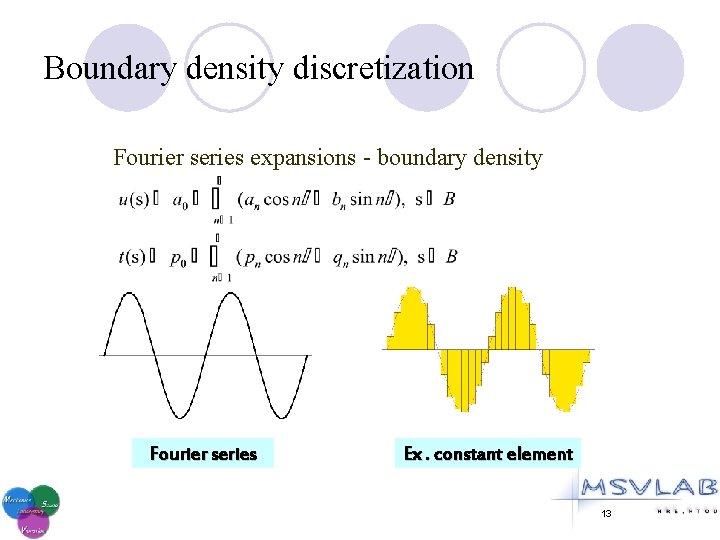
Boundary density discretization Fourier series expansions - boundary density Fourier series Ex. constant element 13

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ ¡ l Numerical examples ¡ ¡ l Superposition technique Addition theorem for the kernel decomposition Fourier expansion for the boundary density Adaptive observer system Linear algebraic equation Green’s function for the concentrated force problems Green’s function for the screw dislocation problems Conclusions 14

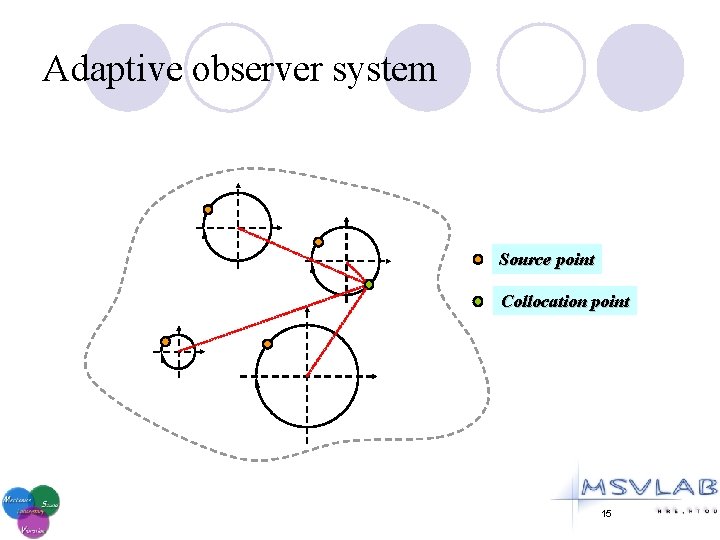
Adaptive observer system Source point Collocation point 15

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ ¡ l Numerical examples ¡ ¡ l Superposition technique Addition theorem for the kernel decomposition Fourier expansion for the boundary density Adaptive observer system Linear algebraic system Green’s function for the concentrated force problems Green’s function for the screw dislocation problems Conclusions 16

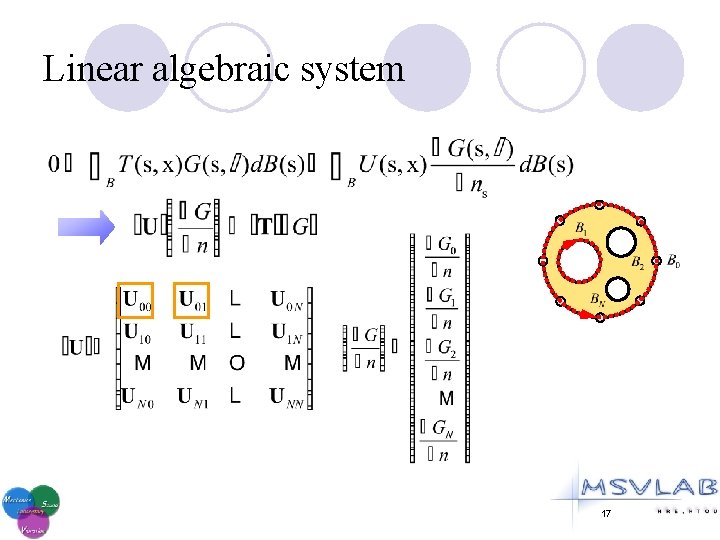
Linear algebraic system 17

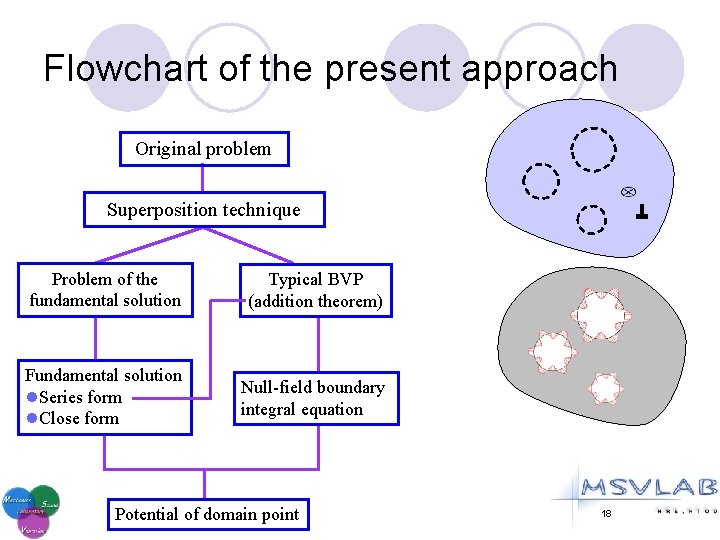
Flowchart of the present approach Original problem Superposition technique Problem of the fundamental solution Typical BVP (addition theorem) Fundamental solution l. Series form l. Close form Null-field boundary integral equation Potential of domain point 18

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ ¡ l Numerical examples ¡ ¡ l Superposition technique Addition theorem for the kernel decomposition Fourier expansion for the boundary density Adaptive observer system Linear algebraic system Green’s function for the concentrated force problems Green’s function for the screw dislocation problems Conclusions 19

Numerical examples l Concentrated force problems ¡ ¡ An annular case An eccentric ring An infinite plane with an aperture subjected to the Neumann boundary condition A half-plane with an aperture (1) Dirichlet boundary condition (2) Robin boundary condition An infinite plane with a circular inclusion l Screw dislocation problems ¡ ¡ An infinite plane with an aperture (1) Dirichlet boundary condition (2) Neumann boundary condition An infinite plane with a circular inclusion An infinite plane with two circular holes subject to the Neumann boundary condition 20

Numerical examples l Concentrated force problems ¡ ¡ An annular case An eccentric ring An infinite plane with an aperture subjected to the Neumann boundary condition A half-plane with an aperture (1) Dirichlet boundary condition (2) Robin boundary condition An infinite plane with a circular inclusion l Screw dislocation problems ¡ ¡ An infinite plane with an aperture (1) Dirichlet boundary condition (2) Neumann boundary condition An infinite plane with a circular inclusion An infinite plane with two circular holes subject to the Neumann boundary condition 21

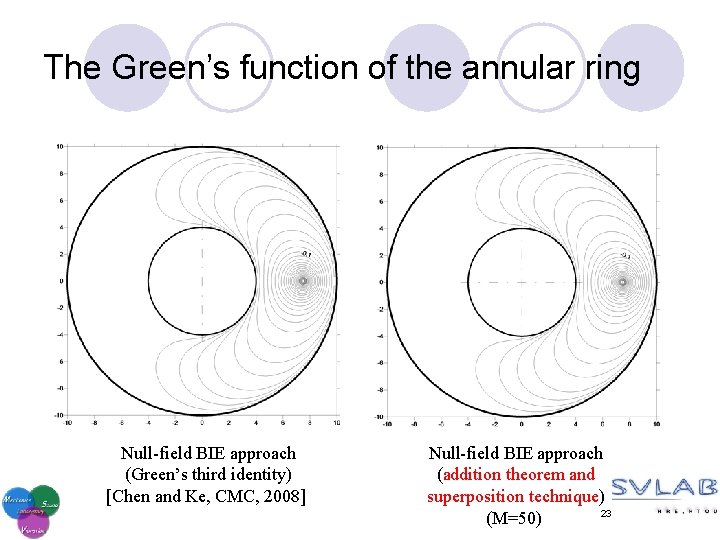
The Green’s function of the annular ring 22

The Green’s function of the annular ring Null-field BIE approach (Green’s third identity) [Chen and Ke, CMC, 2008] Null-field BIE approach (addition theorem and superposition technique) 23 (M=50)

Numerical examples l Concentrated force problems ¡ An annular case ¡ An eccentric ring ¡ An infinite plane with an aperture subjected to the Neumann boundary condition A half-plane with an aperture (1) Dirichlet boundary condition (2) Robin boundary condition An infinite plane with a circular inclusion ¡ ¡ l Screw dislocation problems ¡ ¡ ¡ An infinite plane with an aperture (1) Dirichlet boundary condition (2) Neumann boundary condition An infinite plane with a circular inclusion An infinite plane with two circular holes subject to the Neumann boundary condition 24

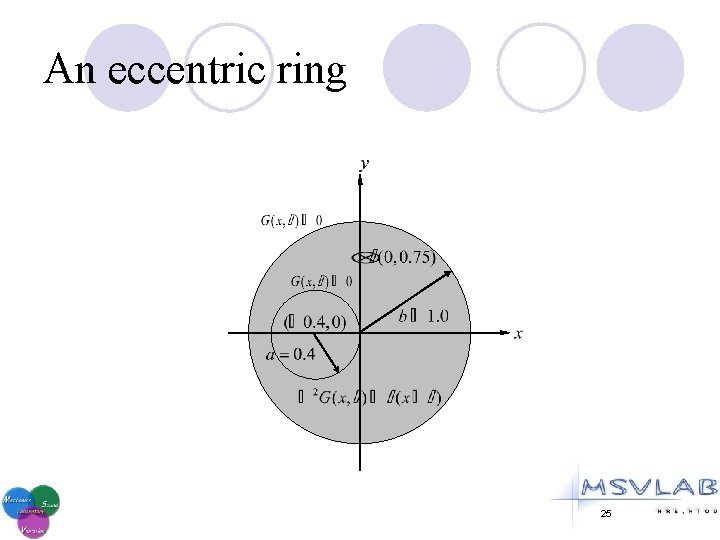
An eccentric ring 25

An eccentric ring Melnikov’s method Null-field BIE approach [Melnikov and Melnikov (2001)] (Green’s third identity) [Chen and Ke, CMC, 2008] Null-field BIE approach (addition theorem and superposition technique) (M=50) 26

Numerical examples l Concentrated force problems ¡ An annular case ¡ An eccentric ring ¡ An infinite plane with an aperture subjected to the Neumann boundary condition A half-plane with an aperture (1) Dirichlet boundary condition (2) Robin boundary condition An infinite plane with a circular inclusion ¡ ¡ l Screw dislocation problems ¡ ¡ ¡ An infinite plane with an aperture (1) Dirichlet boundary condition (2) Neumann boundary condition An infinite plane with a circular inclusion An infinite plane with two circular holes subject to the Neumann boundary condition 27

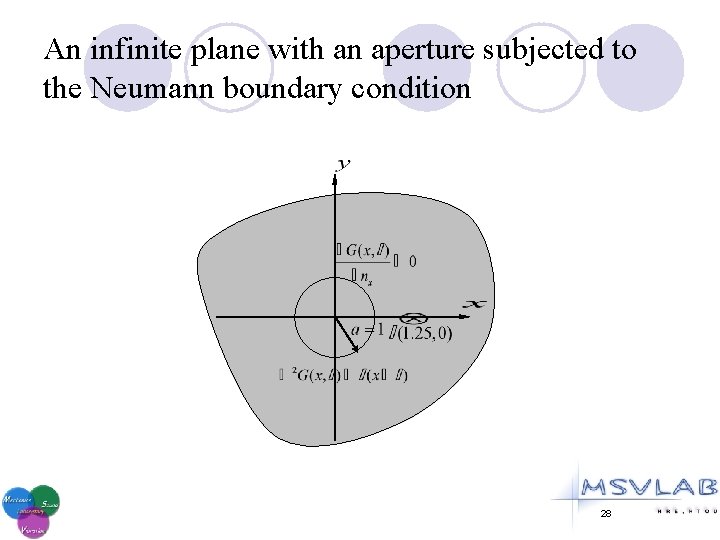
An infinite plane with an aperture subjected to the Neumann boundary condition 28

An infinite plane with an aperture subjected to the Neumann boundary condition Image method Null-field BIE approach (addition theorem and superposition technique) 29 (M=50)

Numerical examples l Concentrated force problems ¡ An annular case ¡ An eccentric ring ¡ An infinite plane with an aperture subjected to the Neumann boundary condition A half-plane problem with an aperture (1) Dirichlet boundary condition (2) Robin boundary condition An infinite plane with a circular inclusion ¡ ¡ l Screw dislocation problems ¡ ¡ ¡ An infinite plane with an aperture (1) Dirichlet boundary condition (2) Neumann boundary condition An infinite plane with a circular inclusion An infinite plane with two circular holes subject to the Neumann boundary condition 30

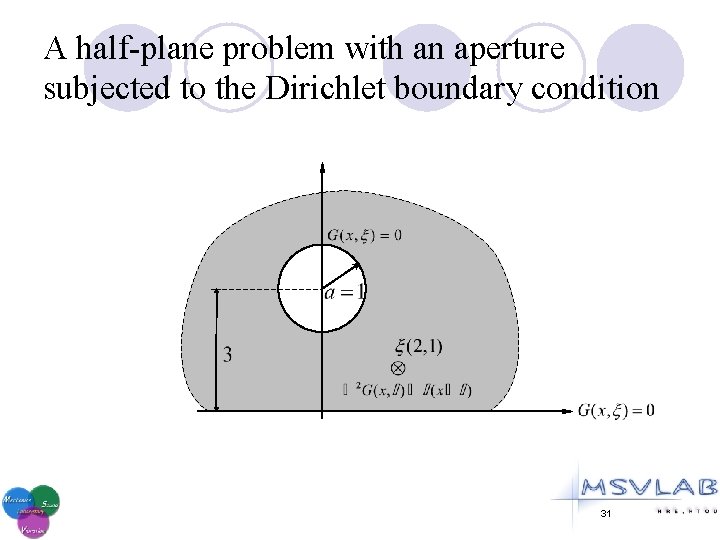
A half-plane problem with an aperture subjected to the Dirichlet boundary condition 31

A half-plane problem with an aperture subjected to the Dirichlet boundary condition Null-field BIE approach Melnikov’s method [Melnikov and Melnikov (2001)] (Green’s third identity) [Chen and Ke, CMC, 2008] Null-field BIE approach (addition theorem and superposition technique) (M=50) 32

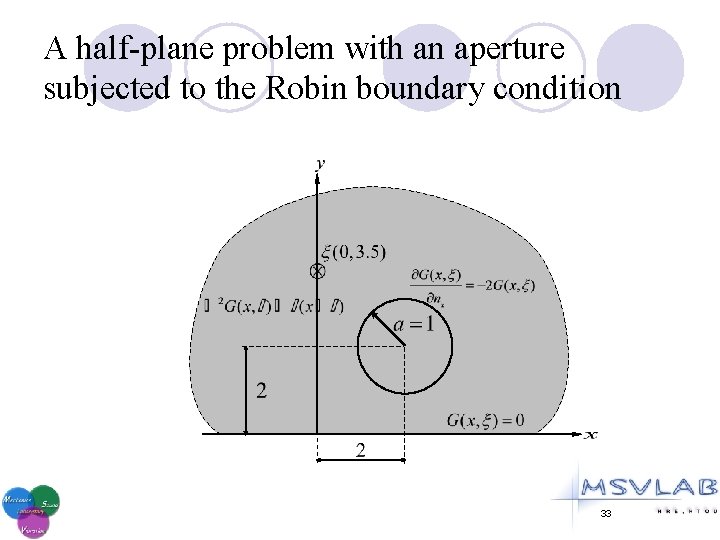
A half-plane problem with an aperture subjected to the Robin boundary condition 33

A half-plane problem with an aperture subjected to the Robin boundary condition Melnikov’s approach [Melnikov and Melnikov (2006)] Null-field BIE approach (Green’s third identity) [Chen and Ke, CMC, 2008] Null-field BIE approach (addition theorem and superposition technique) (M=50) 34

Numerical examples l Concentrated force problems ¡ An annular case ¡ An eccentric ring ¡ An infinite plane with an aperture subjected to the Neumann boundary condition A half-plane with an aperture (1) Dirichlet boundary condition (2) Robin boundary condition An infinite plane with a circular inclusion ¡ ¡ l Screw dislocation problems ¡ ¡ ¡ An infinite plane with an aperture (1) Dirichlet boundary condition (2) Neumann boundary condition An infinite plane with a circular inclusion An infinite plane with two circular holes subject to the Neumann boundary condition 35

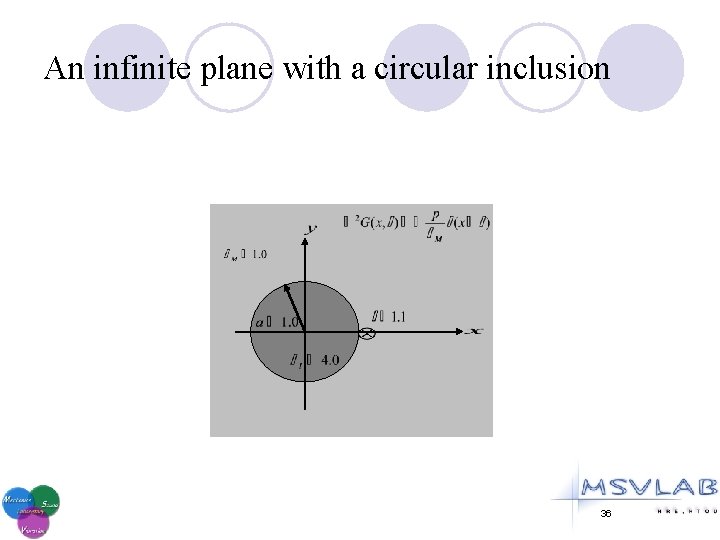
An infinite plane with a circular inclusion 36

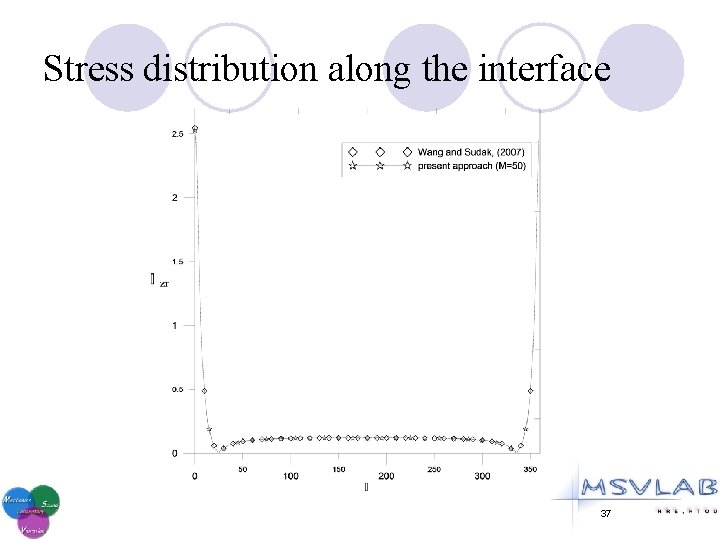
Stress distribution along the interface 37

Equivalence between the solution of Green’s third identity and that of superposition technique = + Green’s third identity Superposition technique 38

Numerical examples l Concentrated force problems ¡ An annular case ¡ An eccentric ring ¡ An infinite plane with an aperture subjected to the Neumann boundary condition A half-plane with an aperture (1) Dirichlet boundary condition (2) Robin boundary condition An infinite plane with a circular inclusion ¡ ¡ l Screw dislocation problems ¡ ¡ ¡ An infinite plane with an aperture (1) Dirichlet boundary condition (2) Neumann boundary condition An infinite plane with a circular inclusion An infinite plane with two circular holes subject to the Numann boundary condition 39

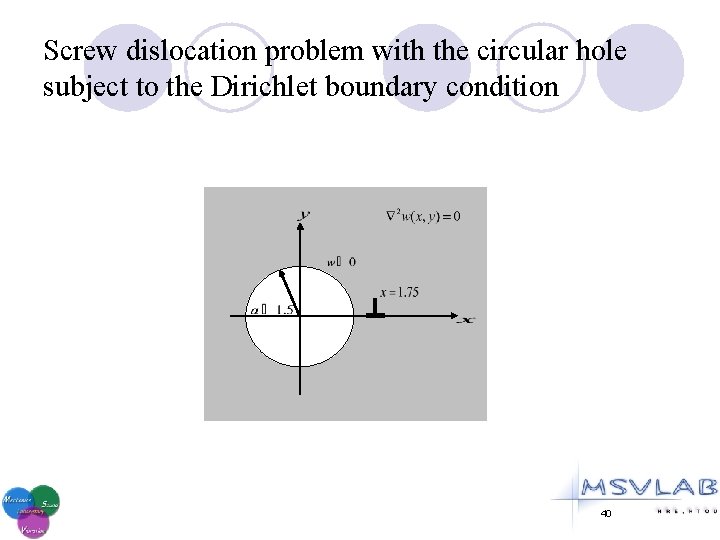
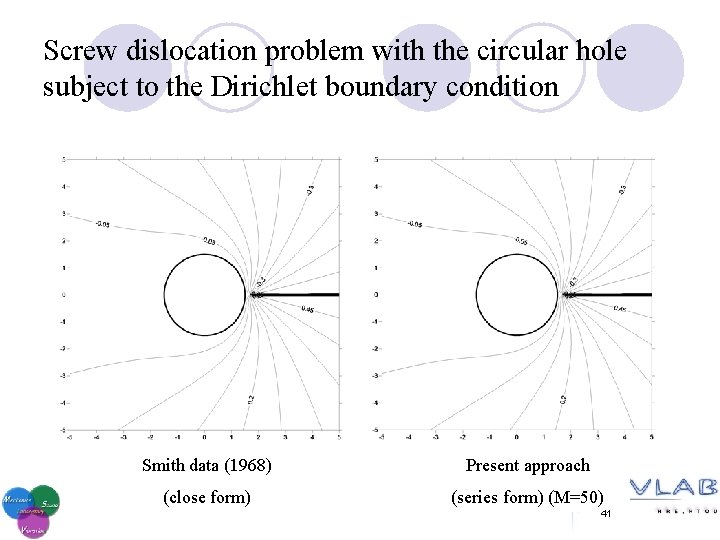
Screw dislocation problem with the circular hole subject to the Dirichlet boundary condition 40

Screw dislocation problem with the circular hole subject to the Dirichlet boundary condition Smith data (1968) Present approach (close form) (series form) (M=50) 41

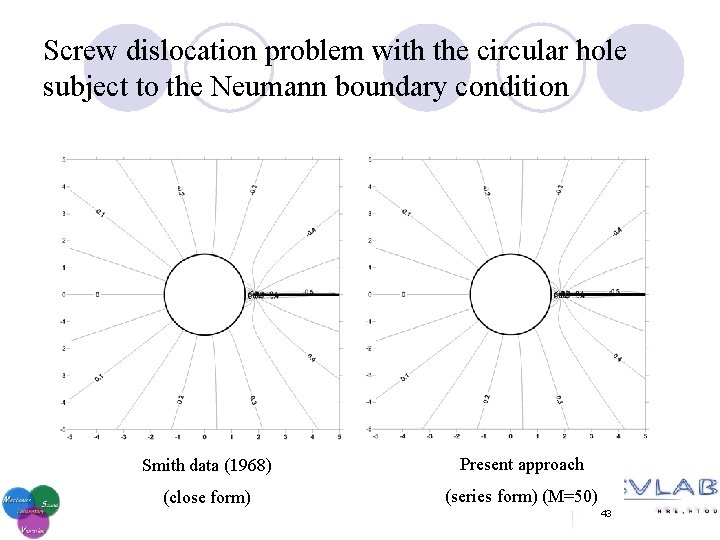
Screw dislocation problem with the circular hole subject to the Neumann boundary condition 42

Screw dislocation problem with the circular hole subject to the Neumann boundary condition Smith data (1968) Present approach (close form) (series form) (M=50) 43

Numerical examples l Concentrated force problems ¡ An annular case ¡ An eccentric ring ¡ An infinite plane with an aperture subjected to the Neumann boundary condition A half-plane with an aperture (1) Dirichlet boundary condition (2) Robin boundary condition An infinite plane with a circular inclusion ¡ ¡ l Screw dislocation problems ¡ ¡ ¡ An infinite plane with an aperture (1) Dirichlet boundary condition (2) Neumann boundary condition An infinite plane with a circular inclusion An infinite plane with two circular holes subject to the Neumann boundary condition 44

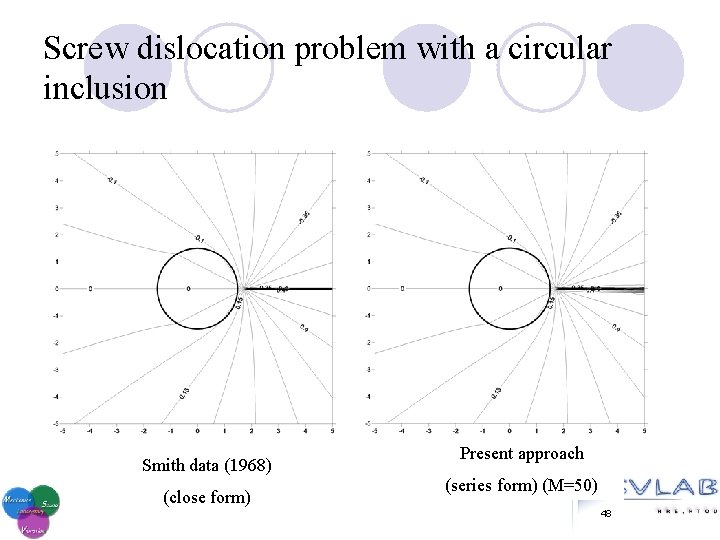
Screw dislocation problem with a circular inclusion 45

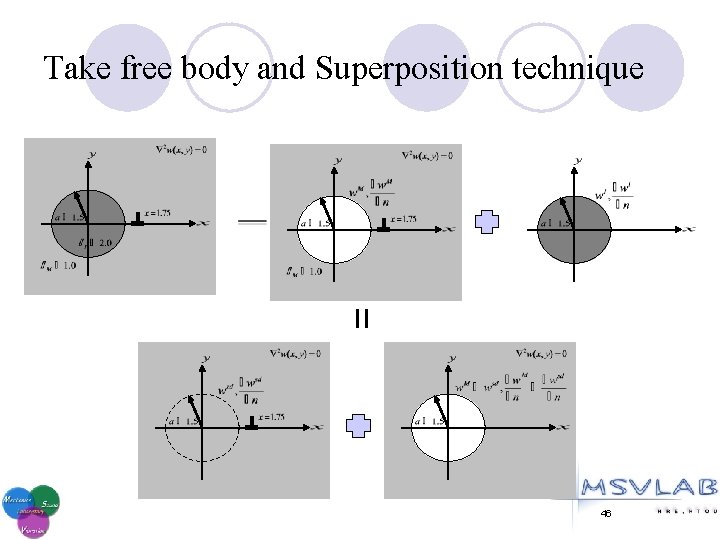
Take free body and Superposition technique 46

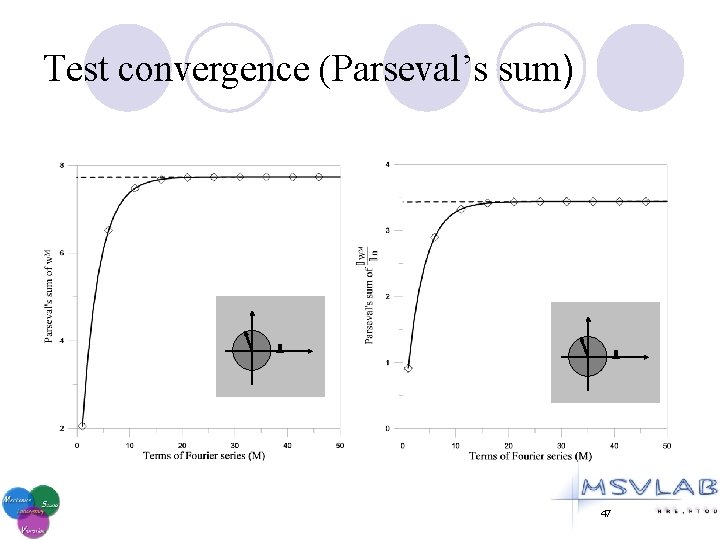
Test convergence (Parseval’s sum) 47

Screw dislocation problem with a circular inclusion Smith data (1968) (close form) Present approach (series form) (M=50) 48

Numerical examples l Concentrated force problems ¡ ¡ ¡ l An annular case An eccentric ring An infinite plane with an aperture subjected to the Neumann boundary condition A half-plane with an aperture (1) Dirichlet boundary condition (2) Robin boundary condition An infinite plane with a circular inclusion Screw dislocation problems ¡ ¡ ¡ An infinite plane with an aperture (1) Dirichlet boundary condition (2) Neumann boundary condition An infinite plane with a circular inclusion An infinite plane with two circular holes subject to the Numann boundary condition 49

Screw dislocation problems with two circular holes subject to the Neumann boundary condition 50

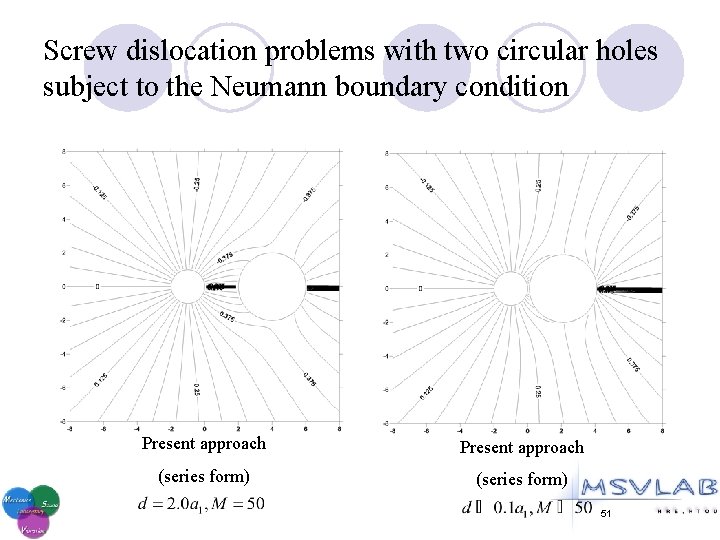
Screw dislocation problems with two circular holes subject to the Neumann boundary condition Present approach (series form) 51

Screw dislocation problems with two circular holes subject to the Neumann boundary condition Present approach (series form) 52

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ ¡ l Numerical examples ¡ ¡ l Superposition technique Addition theorem for the kernel decomposition Fourier expansion for the boundary density Adaptive observer system Linear algebraic system Green’s function for the concentrated force problems Green’s function for the screw dislocation problems Conclusions 53

Conclusions A systematic approach with five advantage singularity free, boundary-layer effect free, exponential convergence, well-posed model and mesh-free generation was developed in this thesis. l The angle-based fundamental solution was successfully expanded into the separable form. l Mathematical equivalence between the Green’s third identity and superposition technique for solving the Green’s function problem was successfully presented. l 54

Further studies l Extension to the imperfect interface. l Derivation the Green’s third identity for the screw dislocation problems. l Extension to the general boundaries. l 2 -D problems to 3 -D problems. 55

The end Thanks for your kind attention. Welcome to visit the web site of MSVLAB: http: //ind. ntou. edu. tw/~msvlab 56

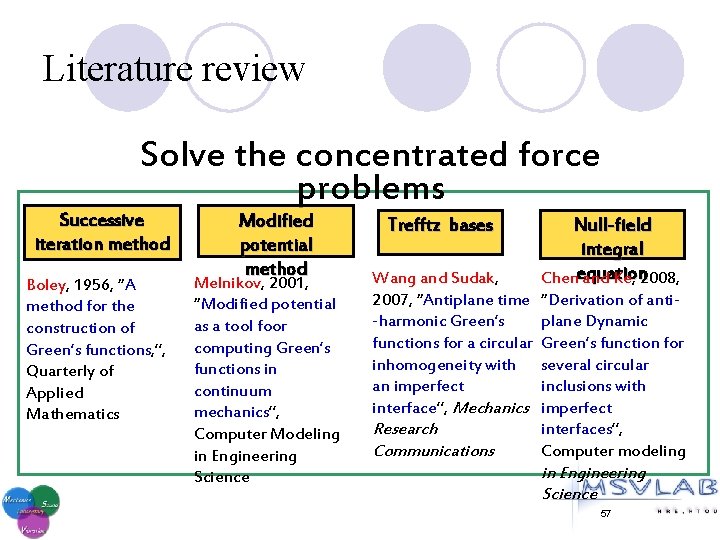
Literature review Solve the concentrated force problems Successive iteration method Boley, 1956, “A method for the construction of Green’s functions, ”, Quarterly of Applied Mathematics Modified potential method Melnikov, 2001, “Modified potential as a tool foor computing Green’s functions in continuum mechanics”, Computer Modeling in Engineering Science Trefftz bases Wang and Sudak, 2007, “Antiplane time -harmonic Green’s functions for a circular inhomogeneity with an imperfect interface”, Mechanics Research Communications Null-field integral Chenequation and Ke, 2008, “Derivation of antiplane Dynamic Green’s function for several circular inclusions with imperfect interfaces”, Computer modeling in Engineering Science 57

Literature review Solve the screw dislocation problems Circle theorem Smith, 1968, “The interaction between dislocations and inhomogeneities-I”, International Journal of Engineering Sciences Image technique Inverse point method Dundurs, 1969, “Elastic interaction of dislocations with inhomogeneities”, Mathematical Theory of Dislocations Sendeckyj, 1970, “Screw dislocation near circular inclusions”, Physica status solidi 58