Applications of addition theorem and superposition technique to

Applications of addition theorem and superposition technique to problems with circular boundaries subject to screw dislocations Reporter: Chou K. H. Advisor: Chen J. T. Data: 2008/06/24 Place: HR 2 307 1

Outline l l Motivation and literature review Derivation of the Green’s function ¡ ¡ l Numerical examples ¡ ¡ ¡ l Superposition technique Addition theorem and boundary density Adaptive observer system Linear algebraic equation Screw dislocation problem with a circular hole subject to Dirichlet or Neumann boundary condition Screw dislocation problem with a circular inclusion Screw dislocation problems with two circular holes subject to Numann boundary condition Conclusions 2

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ l Numerical examples ¡ ¡ ¡ l Superposition technique Addition theorem and boundary density Adaptive observer system Linear algebraic equation Screw dislocation problem with a circular hole subject to Dirichlet or Neumann boundary condition Screw dislocation problem with a circular inclusion Screw dislocation problems with two circular holes subject to Numann boundary condition Conclusions 3

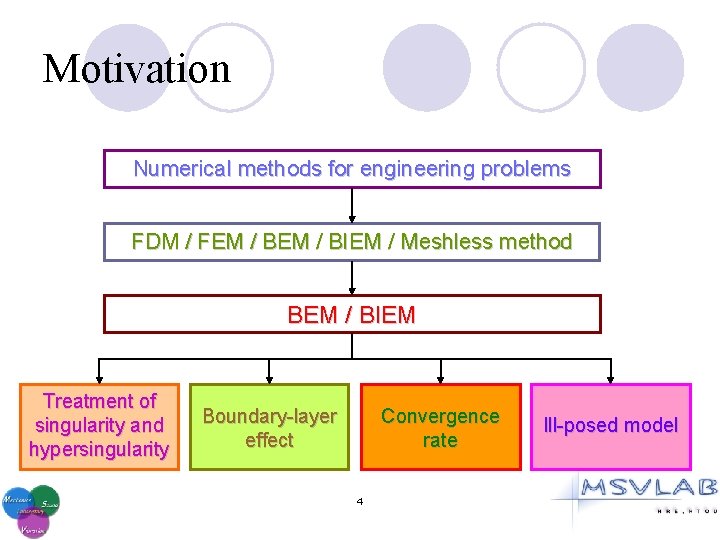
Motivation Numerical methods for engineering problems FDM / FEM / BIEM / Meshless method BEM / BIEM Treatment of singularity and hypersingularity Boundary-layer effect Convergence rate 4 Ill-posed model

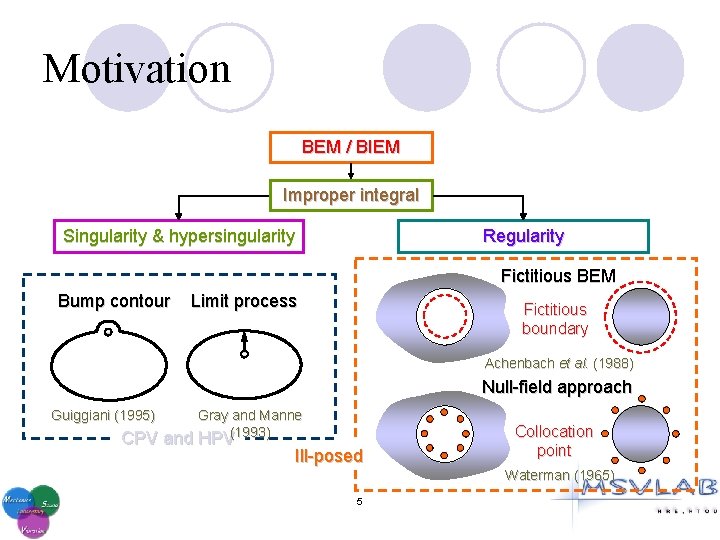
Motivation BEM / BIEM Improper integral Singularity & hypersingularity Regularity Fictitious BEM Bump contour Limit process Fictitious boundary Achenbach et al. (1988) Null-field approach Guiggiani (1995) Gray and Manne HPV(1993) CPV and HPV Ill-posed Collocation point Waterman (1965) 5

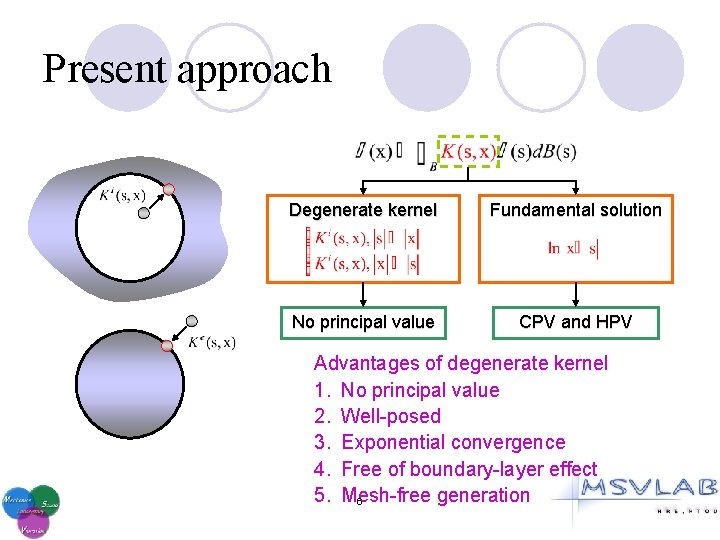
Present approach Degenerate kernel Fundamental solution No principal value CPV and HPV Advantages of degenerate kernel 1. No principal value 2. Well-posed 3. Exponential convergence 4. Free of boundary-layer effect 5. Mesh-free generation 6

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ l Numerical examples ¡ ¡ ¡ l Superposition technique Addition theorem and boundary density Adaptive observer system Linear algebraic equation Screw dislocation problem with a circular hole subject to Dirichlet or Neumann boundary condition Screw dislocation problem with a circular inclusion Screw dislocation problems with two circular holes subject to Numann boundary condition Conclusions 7

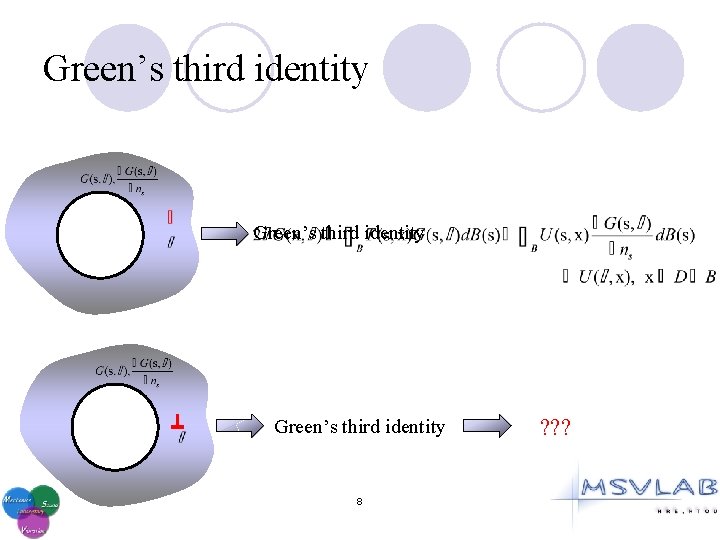
Green’s third identity 8 ? ? ?

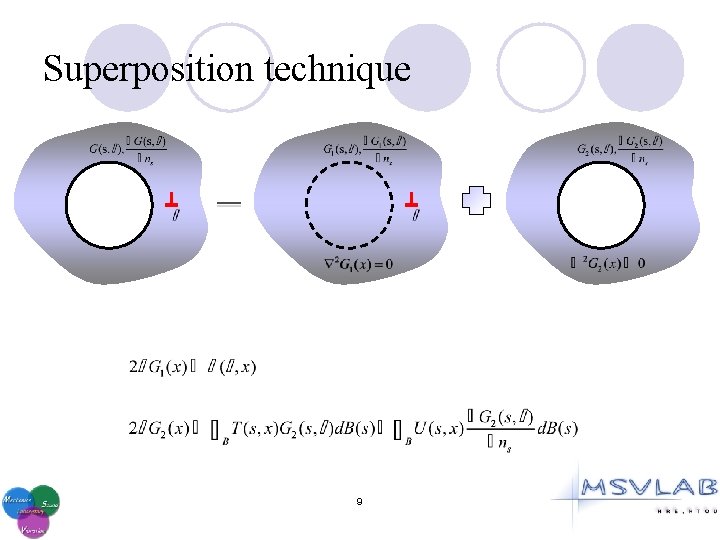
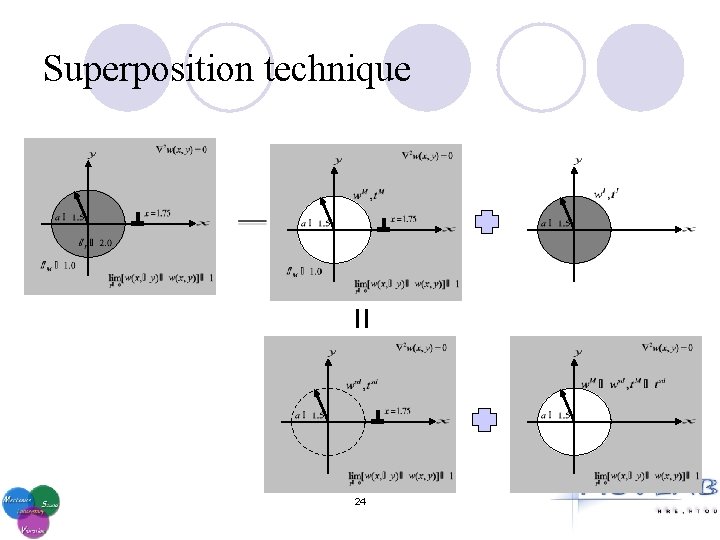
Superposition technique 9

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ l Numerical examples ¡ ¡ ¡ l Superposition technique Addition theorem and boundary density Adaptive observer system Linear algebraic equation Screw dislocation problem with a circular hole subject to Dirichlet or Neumann boundary condition Screw dislocation problem with a circular inclusion Screw dislocation problems with two circular holes subject to Numann boundary condition Conclusions 10

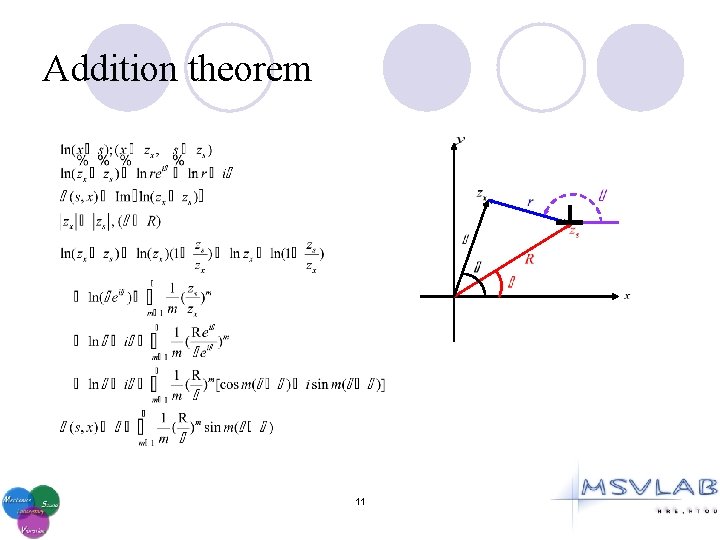
Addition theorem 11

Addition theorem Similarly, modify 12

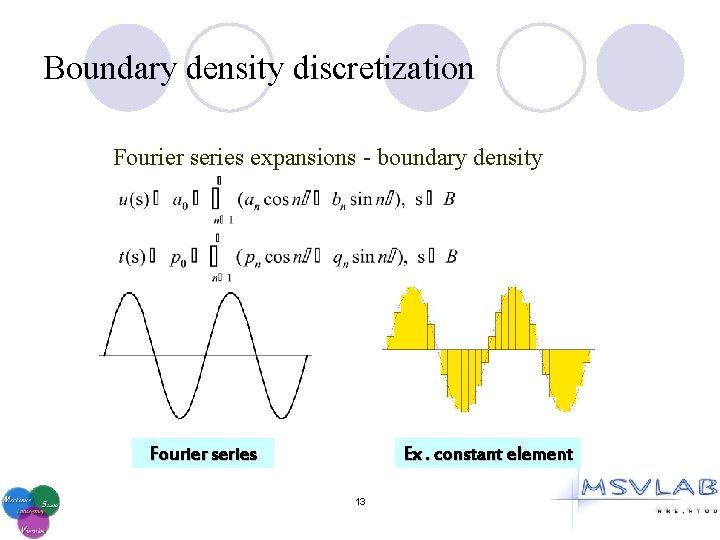
Boundary density discretization Fourier series expansions - boundary density Fourier series Ex. constant element 13

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ l Numerical examples ¡ ¡ ¡ l Superposition technique Addition theorem and boundary density Adaptive observer system Linear algebraic equation Screw dislocation problem with a circular hole subject to Dirichlet or Neumann boundary condition Screw dislocation problem with a circular inclusion Screw dislocation problems with two circular holes subject to Numann boundary condition Conclusions 14

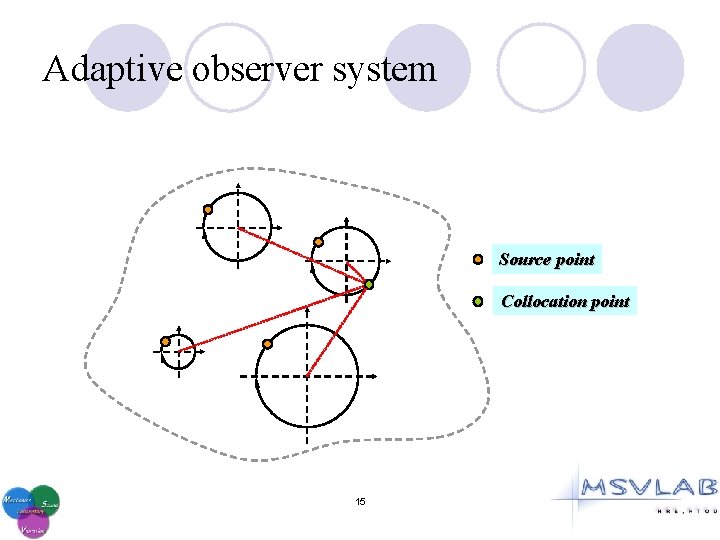
Adaptive observer system Source point Collocation point 15

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ l Numerical examples ¡ ¡ ¡ l Superposition technique Addition theorem and boundary density Adaptive observer system Linear algebraic system Screw dislocation problem with a circular hole subject to Dirichlet or Neumann boundary condition Screw dislocation problem with a circular inclusion Screw dislocation problems with two circular holes subject to Numann boundary condition Conclusions 16

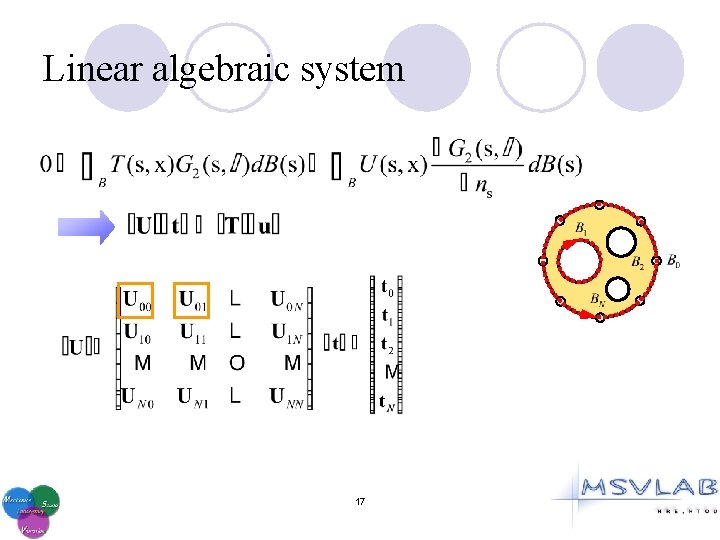
Linear algebraic system 17

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ l Numerical examples ¡ ¡ ¡ l Superposition technique Addition theorem and boundary density Adaptive observer system Linear algebraic system Screw dislocation problem with a circular hole subject to Dirichlet or Neumann boundary condition Screw dislocation problem with a circular inclusion Screw dislocation problems with two circular holes subject to Numann boundary condition Conclusions 18

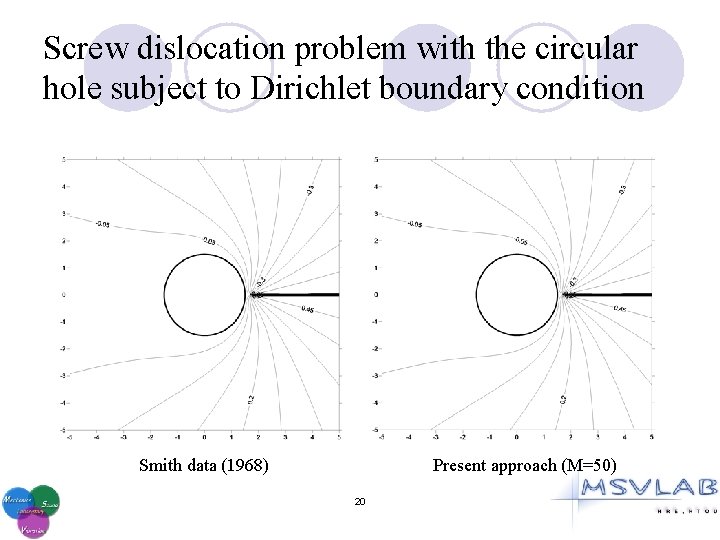
Screw dislocation problem with the circular hole subject to Dirichlet boundary condition 19

Screw dislocation problem with the circular hole subject to Dirichlet boundary condition Smith data (1968) Present approach (M=50) 20

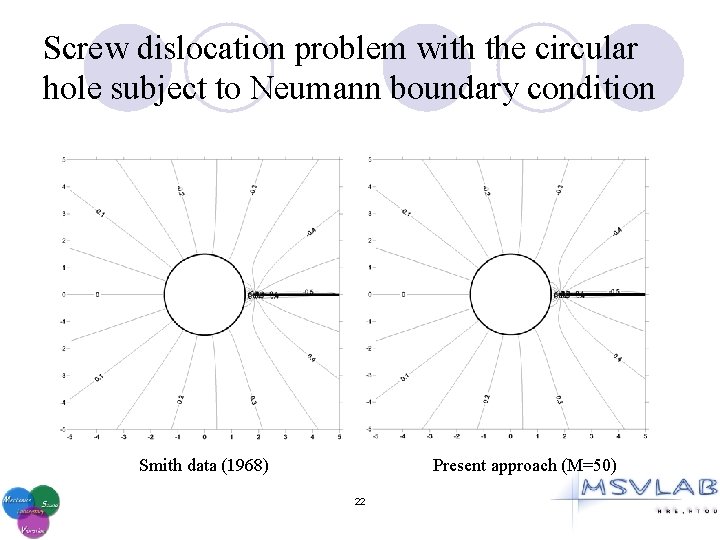
Screw dislocation problem with the circular hole subject to Neumann boundary condition 21

Screw dislocation problem with the circular hole subject to Neumann boundary condition Smith data (1968) Present approach (M=50) 22

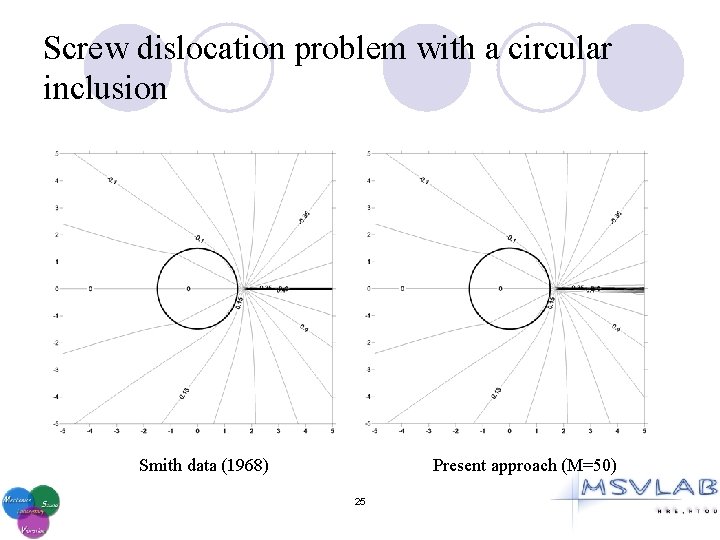
Screw dislocation problem with a circular inclusion 23

Superposition technique 24

Screw dislocation problem with a circular inclusion Smith data (1968) Present approach (M=50) 25

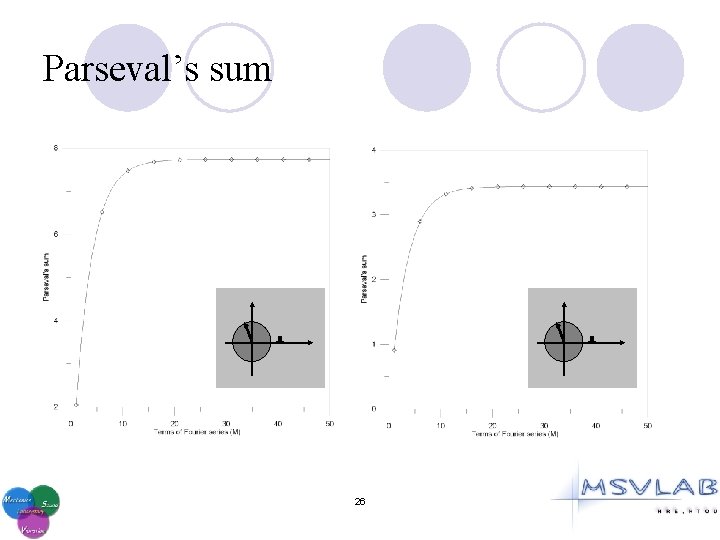
Parseval’s sum 26

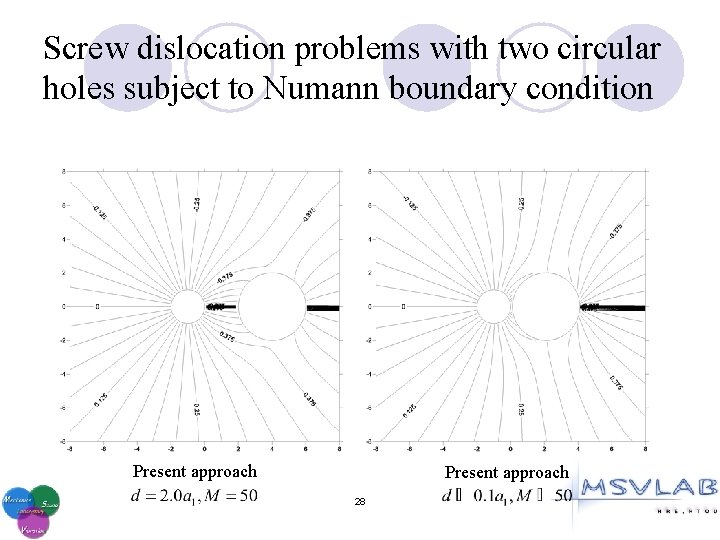
Screw dislocation problems with two circular holes subject to Numann boundary condition 27

Screw dislocation problems with two circular holes subject to Numann boundary condition Present approach 28

Screw dislocation problems with two circular holes subject to Numann boundary condition Present approach 29

Outline Motivation and literature review l Derivation of the Green’s function l ¡ ¡ l Numerical examples ¡ ¡ ¡ l Superposition technique Addition theorem and boundary density Adaptive observer system Linear algebraic system Screw dislocation problem with a circular hole subject to Dirichlet or Neumann boundary condition Screw dislocation problem with a circular inclusion Screw dislocation problems with two circular holes subject to Numann boundary condition Conclusions 30

Conclusions A systematic approach using addition theorem and superposition technique for screw dislocation problems has been successfully proposed. l Five goals of singularity free, boundary-layer effect free, exponential convergence well-posed model and mesh-free generation are achieved. l The results demonstrate the superiority of present approach over the conventional BEM. l 31

The end Thanks for your kind attention. Welcome to visit the web site of MSVLAB: http: //ind. ntou. edu. tw/~msvlab 32