Applications avec la calculatrice SHARP EL 520 ou

Applications avec la calculatrice SHARP EL 520 (ou 546) Configuration (Set up) Angles en degré : 0 –des 0 radians: Pour l’expression angles 0 – 1 Notation(degrés d’affichage FSE (défaut : flottant) ou radians) F Et ixede : 1 l’affichage – 0 emplit l’écran d’affichage SCI entifique : 1 – 1 de la forme 10 n où n ε N ENG eneering: 1 – 2 de la forme 103 n où n ε N

Applications avec la calculatrice SHARP EL 520 (ou 546) Utilisation des constantes (feuillet physical constants)

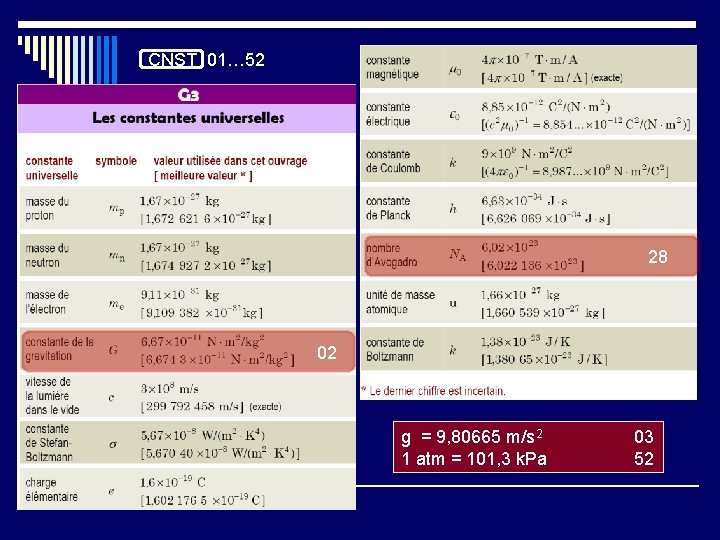
CNST 01… 52 28 02 g = 9, 80665 m/s 2 1 atm = 101, 3 k. Pa 03 52

Applications avec la calculatrice SHARP EL 520 (ou 546) Solution d’équations MODE NORMAL [ 0 ] STAtistics [ 1 ] EQuatio. N [ 2 ] Com. PLe. X [ 3 ]

Do pe nc 4 uv en type tê s tre d’é rés qu olu atio es ns Résolution d’équations (Mode 2) Équations linéaires à 2 inconnues MODE 2 – 0 : 2 Variables Linear Equations a 1 x + a 2 y = a 3 et b 1 x + b 2 y = b 3 Équations linéaires à 3 inconnues MODE 2 – 1 : 3 Variables Linear Equations Équation quadratique: ax 2 + bx + c = 0 MODE 2 – 2 : QUADratic : Équation cubique: ax 3 + bx 2 + cx + d = 0 MODE 2 – 3 : CUBIC :

Résolution d’équations Équations linéaires à 2 inconnues MODE 2 – 0 : 2 Variables Linear Equations a 1 x + a 2 y = a 3 et b 1 x + b 2 y = b 3 Demandera d’entrer les données dans l’ordre: a 1 = ? a 2 = ? a 3 = ? et b 1 = ? b 2 = ? b 3 = ? b 2 = b 3 = On entre la donnée puis enter. À la fin chaque enter affichera: x = y= det = a 1 = a 2 = a 3 = et b 1 = On peut alors résoudre une autre équation en changeant les valeurs. :

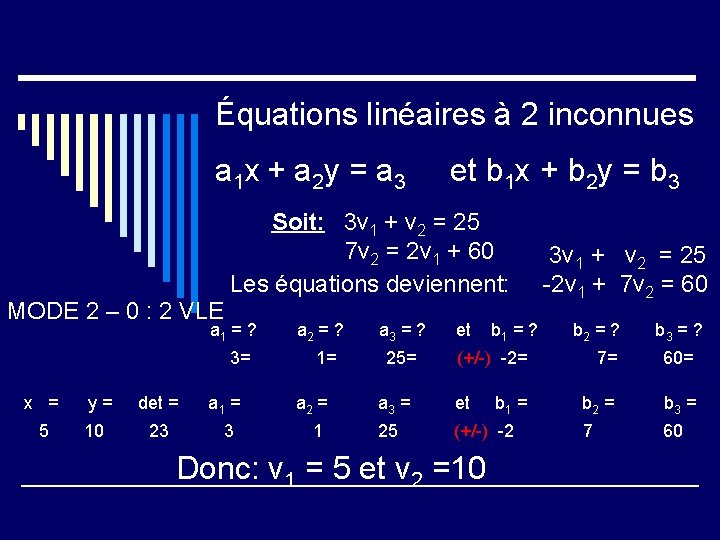
Équations linéaires à 2 inconnues a 1 x + a 2 y = a 3 et b 1 x + b 2 y = b 3 Soit: 3 v 1 + v 2 = 25 7 v 2 = 2 v 1 + 60 Les équations deviennent: MODE 2 – 0 : 2 VLE a 1 = ? 3= x = 5 y= 10 det = a 1 = 23 3 a 2 = ? 1= a 2 = 1 a 3 = ? 25= et b 1 = ? 3 v 1 + v 2 = 25 -2 v 1 + 7 v 2 = 60 b 2 = ? (+/-) -2= a 3 = et 25 (+/-) -2 Donc: v 1 = 5 et v 2 =10 b 1 = b 3 = ? 7= 60= b 2 = b 3 = 7 60

Résolution de l’équation quadratique Équation quadratique: ax 2 + bx + c = 0 MODE 2 – 2 : QUADratic : a=? b=? c=? Pour entrer les valeurs On entre la donnée puis enter. À la fin chaque enter affichera: x 1 = x 2 = a= b= c = On peut alors résoudre une autre équation en changeant les valeurs Attention si xy apparaît à l’écran, il s’agit alors d’une solution irréelle; l’affichage est passée en nombre complexe : alors x 1 = x 2 = la partie réelle. En pressant 2 nd. F et Exp l’affichage sous la forme a + b i

Équation quadratique Soit l'équation: ax 2 + bx + c = 0 25 = 50 - 2 t - 5 t 2 On réécrit l’équation sous la forme : 5 t 2 + 2 t – 25 = 0 MODE 2 – 2 : QUADratic : a=? 5= x 1 = 2. 045 b=? 2= x 2 = -2. 445 a= 5 c=? (+/-) -25= Pour entrer les valeurs b= c 2 -25 Les racines sont donc: +2, 05 et -2, 45

Équation quadratique Soit l'équation: 25 = t - 10 t 2 ax 2 + bx + c = 0 On réécrit l’équation sous la forme : 10 t 2 - t + 25 = 0 MODE 2 – 2 : QUADratic : a=? b=? 10 = (+/-) -1 = x 2 = a= 0. 05 10 c=? Pour entrer les valeurs 25= b= c= -1 -25 Les 2 racines sont donc = +0, 05 xy est apparu au coin supérieur gauche de l’écran ! C’est un irréel ! Retour à x 1: =0. 05 2 nd Exp affiche la partie irréelle : x 1 = 0. 05 + 1. 59 i x 2 : =0. 05 2 nd Exp affiche la partie irréelle : x 2 = 0. 05 - 1. 59 i Mais en physique, un irréel veut dire : il n’y a pas de solution dans le réel ( ou impossible chez les Moldus )

Applications avec la calculatrice SHARP EL 520 (ou 546) Transformation de coordonnées En 2 D seulement, la transformation des coordonnées polaires : ( | r | ; ) en coordonnées cartésiennes (x, y) se fait via les Alors apparaît xy nombres complexes : MODE 3 Les nombres complexes sont exprimés rectangulaires r (affichés sous cette forme par 2 nd r [touche 8]) Ou en coordonnées cartésiennes : a + bi (affichés sous cette forme par 2 nd xy [touche 9])

Expression d’un vecteur dans une autre forme L’entrée des données se fait peu importe le type d’affichage xy ou r : L’angle (touche DMS) ou le i (touche ab/c) indique le type d’entrée. La réponse s’affichera selon le type d’affichage xy 2 nd xy (touche 9) (défaut après avoir entré MODE 3) ou 2 nd r (touche 8) On veut transformer en coordonnées cartésiennes une vitesse de 50 km/h à 40 o (ou à 40 o au nord de l’est) Mode 3 (par défaut nous arrivons en affichage xy) donc: 50 (touche DMS) 40 = 38, 3 2 nd Exp + 32. 14 i vx = 38, 3 km/h et vy = 32, 14 km/h ou

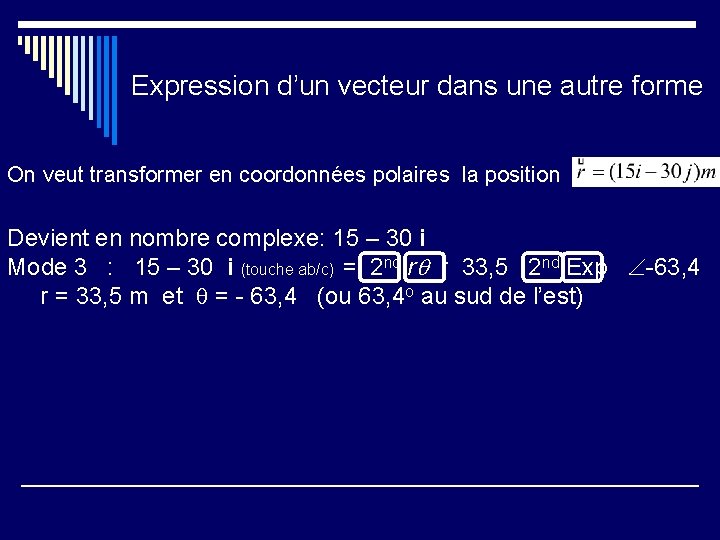
Expression d’un vecteur dans une autre forme On veut transformer en coordonnées polaires la position Devient en nombre complexe: 15 – 30 i Mode 3 : 15 – 30 i (touche ab/c) = 2 nd r : 33, 5 2 nd Exp -63, 4 r = 33, 5 m et = - 63, 4 (ou 63, 4 o au sud de l’est)

Opérations avec les vecteurs On peut entrer les données de n’importe quelle façon, c’est l’affichage qui déterminera si la réponse est en coordonnée cartésienne ou polaire Ex. : MODE 3 3 + 4 i + 6 30 – ( 1 + 6 i ) + 4 (+/-) 40 = 10, 26 2 nd , = -1, 57 Donc = 10, 26 i – 1, 57 j ou 2 nd r : 10, 38 à 2 nd , : - 8, 7 o p a sr Quant au produit, la calculatrice calcule le produit de nombres complexes; mais non le produit scalaire, ni le produit vectoriel pa X